민코프스키 물음표 함수

이 문서에는 일반 참조 목록이 포함되어 있지만 해당 인라인 인용이 충분하지 않습니다. 좀 더 정확한 인용문을 소개하여 이 기사를 개선하는 데 도움을 주시기 바랍니다. (2013년 4월) (이 템플릿 메시지를 제거하는 방법과 시기에 대해 알아보시기 바랍니다.)

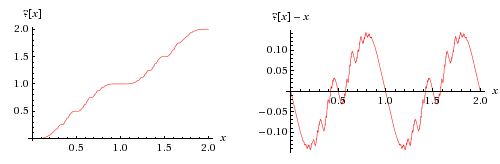
수학에서 민코프스키의 물음표 함수(?(x))는 1904년 헤르만 민코프스키에 의해 정의된 특이한 프랙털 성질을 가진 함수입니다.^[1] 이는 1938년 Arnaud Denjoy가 제시한 유리수의 이진 전개와 직교류의 계속된 분수 전개를 연관시키는 표현을 통해 단위 간격의 유리수에 2차 무리수를 매핑합니다.^[2] 또한 스턴-브로콧 트리와 밀접하게 관련된 재귀적 정의에서 볼 수 있듯이 유리수를 쌍대 유리수에 매핑합니다.

정의와 직관

물음표 함수를 정의하는 한 가지 방법은 유한 또는 무한 이진 수열을 사용하여 분수 수를 표현하는 두 가지 다른 방법 간의 대응을 포함합니다. 가장 친숙한 것은 "11.001001000011111..."과 같이 0과 1로 이루어진 하나의 점 표시가 있는 문자열을 숫자의 이진법으로 해석할 수 있다는 것입니다. 이 경우 이 번호는

$${\displaystyle 2+1+{\frac {1}{8}}+{\frac {1}{64}}+\cdots =\pi .}$$

그러나 같은 수열을 해석하는 방법은 연속적인 분수를 사용하는 것과는 다릅니다. 같은 방법으로 분수 부분 "0.001001000011111..."을 이진수로 해석하면 0 또는 1의 각 연속 블록을 실행 길이(또는 0의 첫 번째 블록의 경우 실행 길이 + 1)로 대체합니다. 이 경우 시퀀스${\displaystyle }$[${\displaystyle 3;}$ ${\displaystyle 3}$, 1${\displaystyle ,}$ ${\displaystyle 2,}$ ${\displaystyle 1,}$ ${\displaystyle 4,}$ 5${\displaystyle ,}$ ${\displaystyle \dots ]}$ ${\displaystyle [3;3, 1,$2, 1,$1, 4,$ 5,\$dots ]}$을 생성합니다$.$ 그런 다음, 이 시퀀스를 연속 분수의 계수로 사용합니다.^[3][4]

$${\displaystyle 3+{\frac {1}}{\displaystyle 3+{\frac {1}{\displaystyle 2+{\frac {1}{\displaystyle 1+{\frac {1}{\frac {1}{\displaystyle 4+{\frac {1}{\displaystyle 5+\dots }}}}:\approx 3.2676}$$

물음표 함수는 주어진 실수의 연속 분수를 런 길이 인코딩된 이진수열로 변환한 다음 해당 수열을 이진수로 재해석하는 과정을 반전시킵니다.^[3][4] 예를 들어 ${\displaystyle \mathrm{위}}$의 예를 들어$$? ⁡ (3$)$ ≈ π {\displaystyle \operatorname {?} (3.2676)\approx \pi}. 이를 공식적으로 정의하려면 무리수 x {\displaystyle x}에 (종료되지 않는) 연속 분수 표현이 있는 경우

$${\displaystyle x=a_{0}+{\frac {1}{\displaystyle a_{1}+{\frac {1}{\displaystyle a_{2}+\cdots}}}=[a_{0};a_{1},a_{2},\dots]}$$

$그러면{\displaystyle }$ x ${\displaystyle x}$의 물음표 함수의 값은 무한급수의 값으로 정의됩니다$$.

$${\displaystyle \operatorname {?} (x)=a_{0}+2\sum _{n=1}^{\infty }{\frac {\left(-1\right)^{n+1}}{2^{a_{1}+\cdots +a_{n}}}}.}$$

마찬가지로, ${\displaystyle }$ x$${\$displaystyle$ x$}$가 종료 연속-분수${\displaystyle }$표현${\displaystyle {}_{}}$[${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$;${\displaystyle {}_{}}$a ${\displaystyle {}_{}}$, a $]$ {\$displaystyle$ [$a_{0}; a_{1$},$a_{$2},\$dots, a_{m$}}의 물음표 $함수$ 값은$유한합$입니다.

$${\displaystyle \operatorname {?} (x)=a_{0}+2\sum _{n=1}^{m}{\frac {\left(-1\right)^{n+1}}{2^{a_{1}+\cdots +a_{n}}}}.}$$

물음표 함수가 연속된 분수를 이진수로 재해석하는 방식과 유사하게, 칸토어 함수는 3진수를 이진수로 재해석하는 것으로 이해될 수 있습니다.

자기대칭성

물음표는 분명히 시각적으로 자체적으로 유사합니다. 단위 제곱에 작용하는 두 연산자 S와 R에 의해 자기 유사성의 모노이드가 생성될 수 있으며 다음과 같이 정의됩니다.

$${\displaystyle {\begin{aligned}S(x,y)&=\left({\frac {x}{x+1}},{\frac {y}{2}}\right),\\[5px]R(x,y)&=(1-x,1-y).\end{align}}}$$

시각적으로 S는 단위 제곱을 왼쪽 하단 쿼터로 축소하는 반면 R은 중심을 통해 점 반사를 수행합니다.

?의 그래프 위의 한 점은 단위 구간에서 일부 x에 대한 좌표 (x, ?(x))를 가집니다. ?는 모든 x ∈ [0, 1]에 대하여 다음 항등식을 만족하므로, 이러한 점은 S와 R에 의해 그래프의 다른 점으로 변환됩니다.

$${\displaystyle {\aligned}\operatorname {?} \left ({\frac {x}{x+1}}\right)&={\frac {\operatorname {?}(x)}{2}},\[5 px]\operatorname {?}(1-x)&=1-\operatorname {?}(x).\end{align}}}$$

이 두 연산자는 반복적으로 결합되어 모노이드를 형성할 수 있습니다. 모노이드의 일반적인 요소는 다음과 같습니다.

$${\displaystyle S^{a_{1}}RS^{a_{2}}RS^{a_{3}}\cdots }$$

양의 정수 a₁, a, a₂₃, …의 경우 각 원소는 물음표 함수의 자기 유사성을 설명합니다. 이 모노이드는 주기 배가 모노이드(period-double monoid)라고 불리기도 하며, 모든 주기 배가 프랙탈 곡선은 이에 의해 설명되는 자기 대칭을 갖습니다(물음표가 특수한 경우인 드 람 곡선은 이러한 곡선의 범주입니다). 모노이드의 요소는 a₁, a₂, a₃, a, …의 식별을 통해 유리수와 일치하며 [0; a₁₂, a₃, a, …]는 연속 분수와 일치합니다. 둘 다 이래로.

$${\displaystyle S:x\map to {\frac {x}{x+1}}$$

$${\displaystyle T:x\maps to 1-x}$$

이차 무리수

물음표 함수는 비다이어틱 유리수에서 2차 무리수로 일대일 매핑을 제공하므로 후자의 계산 가능성을 명시적으로 증명할 수 있습니다. 사실 이것들은 다이애딕 변환을 위한 주기적 궤도에 해당하는 것으로 이해될 수 있습니다. 이는 단 몇 단계로 명확하게 입증할 수 있습니다.

다이아딕 대칭

왼쪽 이동과 오른쪽 이동, 단위 $간격{\displaystyle \mathrm{}}$ ${\displaystyle 0}$ ${\displaystyle \le }$ x ${\displaystyle \le }$ ${\displaystyle 1}$ ${\display 0\leq x\leq$ 1$}$에서 유효한 두 이동을 다음과$$ 같이 정의합니다.

$${\displaystyle L_{D}(x)={\frac {x}{2}}$$

$${\displaystyle R_{D}(x)={\frac {1+x}{2}}}$$

$${\displaystyle L_{D}\circ {\text{?}}={\text{?}}\circ L_{C}}$$

$${\displaystyle R_{D}\circ {\text{?}}={\text{?}}\circ R_{C}}$$

$${\displaystyle L_{D}R_{D}L_{D}L_{D}R_{D}\circ {\text{?}}={\text{?}}\circ L_{C}R_{C}L_{C}L_{C}R_{C}}$$

일부 표기법 재배열은 위의 내용을 약간 더 쉽게 표현할 수 있습니다. ${\displaystyle {g\mathrm{}}_{}}$ 0 ${\$ g 1 ${\$는 L과 R을 나타냅니다$$. $함수$ 구성은 g ${\displaystyle {010}_{}}$ = g ${\displaystyle 0}$ 1 g 0 $display g_{$010} = g_{0} g_{1} g_{0}을 쓸 수 있는 모노이드로 확장됩니다. 일반적으로 g Ag B = g AB {\display g_{$A}g_{B}=g_{$$AB}}$는 숫자 A, B의 일부 이진 문자열에 대해$$ AB는 그러한 문자열의 일반적인 연결입니다. 그러면 다이아딕 모노이드 M은 이러한 모든 유한 길이의 좌우 움직임의 모노이드입니다. γ ∈$M$ {\displaystyle \gamma \in M}을(를) 모노이드의 일반 요소로 쓰면 해당되는 물음표 함수의 자기 대칭이 있습니다.

$${\displaystyle \gamma _{D}\circ {\text{?}}={\text{?}}\circ \gamma _{C}}$$

동형

반사 연산자를 제공하여 유리수와 쌍대 유리수 사이의 명시적인 매핑을 얻을 수 있습니다.

$${\displaystyle r(x)=1-x}$$

$${\displaystyle r\circ R_{D}\circ=L_{D}}$$

${\displaystyle \mathrm{그리고}}$ $r$ ∘ R ${\displaystyle C_{}}$ ∘ $r$= L$C {\$display r\$circ$ R_{C$}\$circ r = L_{C}} {\display r^{2} = 1}이 항등식이므로 임의의 좌-우 이동 문자열은 왼쪽 이동 문자열로만 다시 쓰고, 그 다음에 반사, 더 많은 왼쪽 이동, 반사 등으로 다시 쓸 수 있습니다. ${\displaystyle {La}^{}}$ ${\displaystyle {1_{}}^{}}$ r ${\displaystyle {La}^{}}$ 2 ${\displaystyle {{}_{}}^{}}$ ${\displaystyle {La}^{}}$ $3$⋯ ${\displaystyle$L^{a_${1}}$rL^{a_{2}} rL^{a_{3}}\cdots} Sa 3 ⋯ {\displaystyle S^{a_{1}}$TS^{a_{2}}$$TS^{a_{3}}\cdots}$ 위에서$$. 함수 $인수$ $x$ = ${\displaystyle 1}$ ${\displaystyle$ x = $1}$에서 ${\displaystyle {LD}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle D_{}}${\$displaystyle L_{D}, R_{D}$의 일부 명시적인 시퀀스를 평가하면 dyadic rational이 제공됩니다. 명시적으로$$y = 0$.$ b 1 b 2 b 3 ⋯ bm {\displaystyle y = 0과 같습니다.$b_{1}b_{2}b_{3}\cdots b_{m}},$ 여기서 $각$ ${\displaystyle \mathrm{bk}}$$∈$ {$0$, 1} ${\displaystyle$b_{$k}\$in \{0, 1\}는 왼쪽 이동에 해당하는 0과 오른쪽 이동에 해당하는 하나의 이진 비트입니다. The equivalent sequence of ${\displaystyle L_{C},R_{C}}$ moves, evaluated at ${\displaystyle x=1}$ gives a rational number ${\displaystyle p/q.}$ It is explicitly the one provided by the continued fraction ${\displaystyle p/q=[a_{1},$$a_{2},a_{3},\ldots,a_{j}}$ 수열$({\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {a\mathrm{}}_{}}$ 2${\displaystyle {}_{}}$ a ${\displaystyle {3\mathrm{}}_{}\dots ,}$ ${\displaystyle a_{}}$ ${\displaystyle(a_{1},a_{2},a_{3},\ldots,a_{j})}$가 유한한 길이이기$$ 때문에 유리수임을 염두에$$ 두십시오. 이것은 쌍대 유리수와 유리수 사이의 일대일 대응 관계를 확립합니다.

다이아딕 변환의 주기적 궤도

이제 다이아딕 변환의 주기적인 궤도를 생각해 보세요. 이들은 비트 $b{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {b\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {b\mathrm{}}_{}}$ ${\displaystyle {}_{}\dots ,}$ ${\displaystyle b_{}}$ ${\displaystyle {\mathrm{k}}_{}}$- 1 ${\$의 유한한 초기 "혼란" 시퀀스로 구성된 비트 시퀀스에 해당하며$,$ 이어서 반복되는 $문자열{\displaystyle {}_{}}$ b${\displaystyle {}_{}{k}_{}}$, ${\displaystyle {\mathrm{b}k}_{}}$ + 1${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ k${\displaystyle {}_{}}$+ ${\displaystyle 2_{}\dots ,}$ ${\displaystyle b_{}}$ k${\displaystyle {}_{}}$+ ${\displaystyle {\mathrm{m}}_{}}$- 1 ${\$길이 $m{\displaystyle }$ ${\displaystyle$ m$}$의 $b_{k+m-1$$\}\}.$ 이러한 반복 문자열은 유리수에 해당합니다. 이것은 쉽게 명시됩니다. 쓰기

$${\displaystyle y=\sum _{j=0}^{m-1}b_{k+j}2^{-j-1}}$$

$${\displaystyle \sum _{j=0}^{\infty }b_{k+j}2^{-j-1}=y\sum _{j=0}^{\infty }2^{-jm}={\frac {y}{1-2^{m}}}}$$

연속 분수로서의 주기적 궤도

그러한 주기적 궤도는 위에서 확립된 동형에 따라 동등한 주기적 연속 분율을 갖습니다. 유한한 길이의 초기 "혼란스러운" 궤도가 있고, 그 다음에 반복되는 순서가 있습니다. 반복 시퀀스는 $x$ =${\displaystyle }$[$n,$ n + 1, n + 2, …, n + r, x ]를 만족하는 주기적 연속 분수를 생성합니다$.$ {\displaystyle x = [a_{n}, a_{n+1}, a_{n+2},\ldots, a_{n+r}, x].$}$이$$ 연속된 분수는 다음과^[5] 같은 형태를 갖습니다.

$${\displaystyle x={\frac {\alpha x+\beta }{\gamma x+\delta }}}$$

$${\displaystyle S\map to {\begin{pmatrix}1&0\\\1&1\end{pmatrix}}$$

$${\displaystyle S^{n}\map to {begin{pmatrix}1&0\n&1\end{pmatrix}}}$$

$${\displaystyle T\map to {\begin{pmatrix}-1&1\\\0&1\end{pmatrix}}$$

$${\displaystyle S^{a_{n}}TS^{a_{n+1}}T\cdots TS^{a_{n+r}}={\begin{pmatrix}\alpha &\beta \\\gamma &\delta \end{pmatrix}}}$$

명시적으로 풀면 ${\displaystyle x}$ 2 +${\displaystyle (}$δ - α) x -$β$ = 0이라는${\displaystyle }$γ를 갖게 됩니다. {\displaystyle \gamma x^{2}+(\delta -\alpha )x-\beta =0.} 이에 대한 해가 이차 무리수의 정의를 만족하는지 확인하는 것은 어렵지 않습니다. 사실 모든 2차 무리수는 이런 식으로 표현될 수 있습니다. 따라서 2차 무리수는 다이아딕 변환의 주기적 궤도와 일대일 대응 관계에 있으며, 다이아딕 유리와 일대일 대응 관계에 있는 (비다이아딕) 유리와 일대일 대응 관계에 있습니다. 물음표 기능은 각 경우의 대응 관계를 제공합니다.

?(x)의 속성

물음표 함수는 엄격하게 증가하고 연속적이지만 ^[6]절대적으로 연속적인 함수는 아닙니다. 도함수는 거의 모든 곳에서 정의되며, 0(모든 유리수를 포함하여 거의 모든 곳에서 그 값)과 $+$ ∞ {\$displaystyle$infty}의 두 가지 값만을 취할 수 있습니다. 도함수를 적분하면 물음표 함수를 얻을 수 있는 몇 가지 구성이 있습니다. 그러한 구성 중 하나는 실수선 상의 Farey 숫자의 밀도를 측정함으로써 얻어집니다. 물음표 측도는 때때로 다중 분수 측도라고 하는 것의 원형적인 예입니다.

물음표 함수는 유리수를 쌍대 유리수에 매핑하는데, 이는 위에서 설명한 재귀적 구성에서 유도하여 증명할 수 있는 것처럼 기본 2개의 표현이 종료되는 유리수를 의미합니다. 2차 무리수를 비다이어트 유리수에 매핑합니다. 두 경우 모두 이 집합들 사이에 순서 동형을 제공하여,^[8] 두 개의 무한히 셀 수 있는 조밀한 선형 순서가 순서 동형인 구체적인 칸토어의 동형 정리를 만듭니다.^[9] 이것은 홀수 함수이며, 함수식 ?(x + 1) = ?(x) + 1을 만족합니다. 결과적으로 x ↦ ?(x) - x는 주기가 1인 홀수 주기 함수입니다. 만약 ?(x)가 무리수라면, x는 2보다 큰 대수적이거나 초월적입니다.

물음표 함수는 0으로 고정된 점을 갖습니다. 1/2과 1, 그리고 적어도 두 개 이상은 중간점을 기준으로 대칭입니다. 하나는 약 0.42037입니다.^[6] Moshchevitin은 고정된 점이 5개뿐이라고 추측했습니다.^[10]

1943년 라파엘 ë 살렘은 물음표 함수의 푸리에-슈틸트제 계수가 무한대에서 사라지는지에 대한 문제를 제기했습니다. 다시 말해서, 그는 그가 알고 싶어했는지 아닌지를 알고 싶었습니다.

$${\displaystyle \lim_{n\to \infty}\int_{0}^{1}e^{2\piinx}\,\operatorname {d?}(x)=0.}$$

Jordan과 Sahlsten은 Gibbs 조치에 대한 결과의 특별한 경우로서 긍정적으로 대답했습니다.^[12]

민코프스키 물음표 함수의 그래프는 드 람 곡선으로 알려진 프랙탈 곡선의 특별한 경우입니다.

알고리즘.

재귀적 정의는 다음 C 함수가 보여주는 것처럼 임의의 실수에 대해 원하는 정도의 정확도로 함수를 계산하는 알고리즘에 자연스럽게 적합합니다. 알고리즘은 입력 x를 찾아 스턴-브로콧 트리를 내려오고 도중에 y = ?(x)의 이진 확장 조건을 합산합니다. 루프 불변량 qr - ps = 1이 만족되는 한, 분수 m/n = p + r/q + s를 줄일 필요가 없습니다. 이는 이미 가장 낮은 항에 있기 때문입니다. 또 다른 불변량은 p/q ≤ x < r/s입니다. 그 for 이 프로그램의 루프는 다음과 같이 분석될 수 있습니다. while 루프, 처음 세 줄의 조건부 단절 문이 조건을 만들어냅니다. 불변량에 영향을 미칠 수 있는 유일한 문장은 마지막 두 줄에 있으며, 이것들은 처음 세 줄이 루프를 벗어나지 않고 성공적으로 실행되는 한 두 불변량의 진실을 보존하는 것으로 보여질 수 있습니다. 루프 본체에 대한 세 번째 불변량(부동점 정밀도까지)은 y ≤ ?(x) < y + d이지만, 어떤 조건도 테스트하기 전에 루프 시작 시 d가 절반으로 줄어들기 때문에, 우리의 결론은 루프 종료 시 y ≤ ?(x) < y + 2d뿐입니다.

해지를 증명하기 위해서는 그 합계가 q + s 루프를 반복할 때마다 최소 1씩 증가하며, 이 합계가 너무 커서 원시 C 데이터 유형으로 표현할 수 없을 때 루프가 종료됩니다. long. 하지만 실제로는 조건부 브레이크는 다음과 같습니다. y + d == y 합리적인 시간 내에 루프가 종료되도록 보장하는 기능입니다.

/* 민코프스키의 물음표 함수 */ 두 배의 민코프스키(두 배의 x) {     긴 p = x;     긴 q = 1, r = p + 1, s = 1, m, n;     두 배의 d = 1, y = p;     한다면 (x < p    (p < 0) ^ (r <= 0))         돌아가다 x; /* 범위를 벗어났습니까?(x) = ~ x */     위해서 (;;) { /* 불변량: q * r - p * s == 1 & p / q < = x & x < r / s */         d /= 2;         한다면 (y + d == y)             브레이크.; /* 가능한 최대 정밀도에 도달함 */         m = p + r;         한다면 ((m < 0) ^ (p < 0))             브레이크.; /* 합계가 넘칩니다*/         n = q + s;         한다면 (n < 0)             브레이크.; /* 합계가 넘칩니다*/          한다면 (x < (두 배의)m / n) {             r = m;             s = n;         } 또 다른 {             y += d;             p = m;             q = n;         }     }     돌아가다 y + d; /* 최종 라운드 오프 */ } 

확률분포

민코프스키 물음표 함수를 ?:[0,1] → [0,1]로 제한하여 단위 구간의 특이 분포의 누적 분포 함수로 사용할 수 있습니다. 이 분포는 중간점을 기준으로 대칭이며, 원시 모멘트는 약 m = 0.5, m = 0.290926, m = 0.186389 및 m = 0.126992이며, 따라서 평균과 중위수는 0.5, 표준 편차는 약 0. 2023, 왜도는 0, 초과 첨도는 약 -1.147입니다.

참고 항목

• 폼페이우스 도함수

참고문헌

메모들

사료

서지학

더보기

외부 링크

• 광범위한 서지 목록
• Weisstein, Eric W., "Minkowski's Question Mark Function", MathWorld
• C++에서 간단한 IEEE 754 구현