혼합모델

혼합 모형, 혼합 효과 모형 또는 혼합 오차 성분 모형은 고정 효과와 랜덤 효과를 모두 포함하는 통계 모형입니다.^[1]^[2] 이러한 모델은 물리, 생물 및 사회 과학의 다양한 분야에서 유용합니다. 이러한 변수는 동일한 통계 단위(종방향 스터디)에서 반복 측정이 수행되는 설정이나 관련 통계 단위의 군집에서 측정이 수행되는 경우에 특히 유용합니다.^[2] 혼합 모형은 결측값 처리의 유연성과 반복 측정의 불균일한 간격 때문에 분산 회귀 모형의 전통적인 분석보다 선호되는 경우가 많습니다.^[3]혼합 모형 분석을 사용하면 보다 다양한 상관 관계 및 분산-공분산 구조에서 측정값을 명시적으로 모델링할 수 있습니다.

이 페이지에서는 일반화된 선형 혼합 모델이나 비선형 혼합 효과 모델보다는 주로 선형 혼합 효과 모델(LMEM)에 대해 설명합니다.

정성적 설명

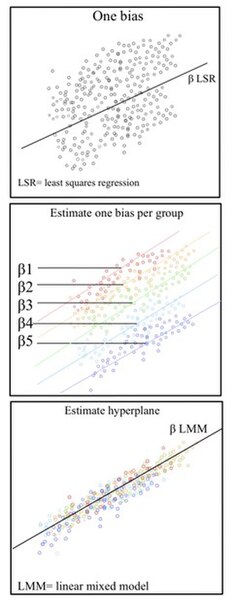
선형 혼합 모형(LMM)은 비독립적인 데이터 구조를 정확하게 나타내기 위해 고정 효과와 랜덤 효과를 통합하는 통계 모형입니다. LMM은 분산 분석의 대안입니다. 종종 분산 분석에서는 각 그룹 내 관측치의 독립성을 가정하지만 이 가정은 다중 수준/계층적, 종단적 또는 상관 데이터 세트와 같은 독립적이지 않은 데이터에는 적용되지 않을 수 있습니다.

비독립 집합은 결과 간의 변동성이 그룹 내 또는 그룹 간의 상관 관계로 인해 발생하는 집합입니다. 혼합 모형은 관측치가 중첩된 연관성에 의해 영향을 받는 둥지 구조/계층적 데이터 구조를 적절하게 설명합니다. 예를 들어, 여러 학교가 참여하는 교육 방법을 공부할 때 고려해야 할 여러 수준의 변수가 있습니다. 개인 수준/하위 수준은 학교 내 개별 학생 또는 교사로 구성됩니다. 이 학생/교사로부터 얻은 관측치는 소속 학교 내에 내포되어 있습니다. 예를 들어, 학생 A는 학교 A 내의 단위입니다. 다음으로 높은 단계는 학교입니다. 고등 수준에서 학교는 여러 명의 개별 학생과 교사를 포함합니다. 학교 수준은 학생과 교사로부터 얻은 관찰에 영향을 미칩니다. 예를 들어, 학교 A와 학교 B는 각각 학생 A와 학생 B의 집합으로 상위 수준입니다. 이것은 계층적 데이터 체계를 나타냅니다. 계층적 데이터를 모델링하는 해결책은 선형 혼합 모델을 사용하는 것입니다.

LMM을 사용하면 데이터 구조에 포함된 비독립성에 대한 표준 오차에 대한 수정 사항을 통합하면서 수준 간 및 수준 내의 중요한 영향을 이해할 수 있습니다.^[4]^[5]

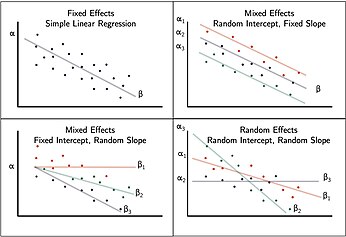
고정 효과

고정 효과는 기본 관심 수준에서 일치하는 경향/경향을 캡슐화합니다. 이러한 효과는 비임의적이고 연구 대상 모집단에 대해 일정하다고 가정하기 때문에 고정된 것으로 간주됩니다.^[5] 예를 들어, 교육을 공부할 때 고정 효과는 모든 학교에서 일관된 전체 학교 수준 효과를 나타낼 수 있습니다.

데이터 집합의 계층 구조는 일반적으로 명확하지만 모든 피실험자의 평균 반응에 영향을 미치는 특정 고정 효과를 지정해야 합니다. 일부 고정 효과 계수는 대응하는 랜덤 효과 없이 충분하지만 다른 고정 계수는 개별 단위가 랜덤인 평균만 나타냅니다. 이들은 무작위 절편과 기울기를 통합하여 결정할 수 있습니다.^[6]

대부분의 상황에서는 여러 관련 모델을 고려하고 보편적인 모델을 가장 잘 나타내는 모델을 채택합니다.

랜덤 효과, ,

혼합 모형의 핵심 구성 요소는 고정 효과에 랜덤 효과를 통합하는 것입니다. 고정 효과는 종종 기본 모형을 나타내기 위해 적합됩니다. 선형 혼합 모형에서 모집단의 실제 회귀 분석은 선형, β입니다. 고정된 데이터가 가장 높은 수준에 적합됩니다. 랜덤 효과는 데이터 계층의 여러 수준에서 통계적 변동성을 도입합니다. 이들은 데이터의 특정 그룹에 영향을 미치는 측정되지 않은 분산 소스를 설명합니다. 예를 들어, 같은 반 학생 1과 학생 2의 차이 또는 같은 학교 학생 1과 학생 2의 차이입니다.

이력 및 현황

Ronald Fisher는 친척 간의 특성 값의 상관 관계를 연구하기 위해 랜덤 효과 모델을 도입했습니다.^[9] 1950년대에 Charles Roy Henderson은 고정 효과에 대한 최상의 선형 편향 추정치와 랜덤 효과에 대한 최상의 선형 편향 예측치를 제공했습니다.^[10]^[11]^[12]^[13] 그 후, 혼합 모델링은 최대 우도 추정 계산, 비선형 혼합 효과 모델, 혼합 효과 모델의 결측 데이터, 혼합 효과 모델의 베이지안 추정에 대한 작업을 포함하여 통계 연구의 주요 영역이 되었습니다. 혼합 모델은 각 관심 단위에 대해 여러 상관 측정이 이루어지는 많은 분야에서 적용됩니다. 유전학에서 마케팅에 이르기까지 다양한 분야에서 인간과 동물 주제를 포함하는 연구에 주로 사용되며 야구 분석 전문가와 혼합 모델 및 산업 통계에도 사용되었습니다.^[15] 혼합 선형 모델 연관성을 통해 잘못된 양의 연관성을 방지할 수 있습니다. 모집단은 서로 깊이 연결되어 있으며 모집단 역학의 관련성 구조는 혼합 모델을 사용하지 않고 모델링하기가 매우 어렵습니다. 그러나 선형 혼합 모형이 유일한 해결책이 될 수는 없습니다. LMM은 연속 및 이진 특성을 고려하거나 깊게 연관시킬 때 때때로 위반되는 일정 잔차 분산 가정을 가지고 있습니다.

정의.

행렬 표기법에서 선형 혼합 모델은 다음과 같이 나타낼 수 있습니다.

{\boldsymbol {y}}=X{\boldsymbol {\beta }+Z{\boldsymbol {u}}+{\boldsymbol {\epsilon}}

어디에

${\boldsymbol {y}}$ ${\boldsymbol {y}$ 은 평균 ${\boldsymbol {y}}$ $E({\boldsymbol {y}})=X{\boldsymbol {\beta }}$ = $E({\boldsymbol {y}})=X{\boldsymbol {\beta }}$ ${\$ displaystyle E({\boldsymbol ${\boldsymbol {y}}$ y}) = X {\boldsymb ${\boldsymbol {y}}$ beta }};
${\boldsymbol {\beta }}$ ${\displaystyle {\boldsymb$ }}은(는) 고정 효과의 알 수 없는 벡터입니다.
${\boldsymbol {u}}$ ${\boldsymbol {u}$ 은(는) $E({\boldsymbol {u}})={\boldsymbol {0}}$ ${\boldsymbol {u}}$ $E({\boldsymbol {u}})={\boldsymbol {0}}$ = ${\$ displaystyle E $({\boldsymbol {$ ${\boldsymbol {u}}$ }}) = {\boldsymbol {0}} 및 ${\boldsymbol {u}}$ ovariance 행렬 ${\boldsymbol {u}}$ var $\operatorname {var} ({\boldsymbol {u}})=G$ ${\boldsymbol {u}}$ (u) = G {\displaystyle \operatorname {var}({\boldsymbol {u})의 알 수 없는 랜덤 효과 벡터입니다. $=G};$
$ϵ$ $E({\boldsymbol {\epsilon }})={\boldsymbol {0}}$ ${\displaystyle$ {\ $boldsymbol {\$ epsilon}}은(는) ${\boldsymbol {\epsilon }}$ $E({\boldsymbol {\epsilon }})={\boldsymbol {0}}$ ${\boldsymbol {\epsilon }}$ ( $ϵ$ $)$ = 0 ${\$ displaystyle E({\boldsymbol {\epsilo ${\boldsymbol {\epsilon }}$ }}) = {\boldsymbol {0}} 및 분산 ${\boldsymbol {\epsilon }}$ v ${\boldsymbol {\epsilon }}$ r ${\boldsymbol {\epsilon }}$ (ϵ) $E({\boldsymbol {\epsilon }})={\boldsymbol {0}}$ R {\displaystyle \operatorname {var}({\boldsymbol {\epsil ${\boldsymbol {\epsilon }}$ n}) = R};
$X$ $X$ 는 $X$ 관찰 ${\boldsymbol {y}}$ ${\$ 에서 $\boldsymbol{y}$ ${\boldsymbol {\beta }}$ ${\$ 까지의 고정 효과에 대한 알려진 설계 행렬입니다 ${\boldsymbol {\beta }}$
$Z {\displaystyle$ Z $}$ 는 $Z$ ${\boldsymbol {u}}$ ${\boldsymbol {y}}$ ${\$ 에서 u ${\$ 까지의 $\boldsymbol{y}$ 랜덤 효과에 대한 알려진 설계 행렬입니다 ${\boldsymbol {u}}$

견적

${\boldsymbol {y}}$ ${\boldsymbol {y}$ 과 u ${\boldsymbol {u}$ 의 조인트 밀도는 $f({\boldsymbol {y}},{\boldsymbol {u}})=f({\boldsymbol {y}}|{\boldsymbol {u}})\,f({\boldsymbol {u}})$ u $f({\boldsymbol {y}},{\boldsymbol {u}})=f({\boldsymbol {y}}|{\boldsymbol {u}})\,f({\boldsymbol {u}})$ = f $y$ u) {\displaystyle f ({\boldsymbol {y}}, {\boldsymbol {u}}, = f ({\boldsymbol {y}, {\boldsymbol {u}},\,f ({\boldsymbol {u}}}와 같이 기록할 수 있습니다. 정상성을 가정할 때, ${\boldsymbol {u}}\sim {\mathcal {N}}({\boldsymbol {0}},G)$ , ${\boldsymbol {\epsilon }}\sim {\mathcal {N}}({\boldsymbol {0}},R)$ and ${\displaystyle \mathrm {Cov} ({\boldsymbol {u}},$ ${\boldsymbol {\epsilon$ }}) $=$ {\ $boldsymbol {0$ ${\boldsymbol {\beta }}$ {\ $displaystyle {\boldsymbol {\u$ }} ${\boldsymbol {u}}$ u {\ $displaystyle$ {\ $boldsymbol {$ u ${\boldsymbol {u}}$ 에 비해 관절 밀도를 최대화하면 선형 혼합 모델에 대한 Henderson의 "혼합 모델 방정식"(MME)을 제공합니다.

{\begin{pmatrix}X'R^{-1}X&X'R^{-1}Z\\Z'R^{-1}X&Z'R^{-1}Z+G^{-1}\end{pmatrix}}{\begin{pmatrix}{\hat {\boldsymbol {\beta }}}\\{\hat {\boldsymbol {u}}}\end{pmatrix}}={\begin{pmatrix}X'R^{-1}{\boldsymbol {y}}\\Z'R^{-1}{\boldsymbol {y}}\end{pmatrix}}

MME, $\textstyle {\hat {\boldsymbol {\beta }}}$ $\textstyle {\hat {\boldsymbol {\beta }}}$ ${\$ 및 $\textstyle {\hat {\boldsymbol {u}}}$ ${\$ {\boldsymbol ${u}}}$ 에 $\textstyle\hat{\boldsymbol{\beta}}$ $\textstyle\hat{\boldsymbol{u}}$ 대한 ${\boldsymbol {\beta }}$ 은 각각 β ${\displaystyle$ {\boldsymbol ${\beta}}$ 및 ${\boldsymbol {\beta }}$ ${\boldsymbol {u}}$ u\ $displaystyle$ {\ $boldsymbol {u}}$ 에 대한 최상의 선형 편향되지 않은 추정치 및 ${\boldsymbol {u}}$ 변수입니다 ${\boldsymbol {u}}$ 이것은 결과의 조건부 분산이 항등 행렬로 확장할 수 없을 때 가우스-마르코프 정리의 결과입니다. 조건부 분산이 알려져 있을 때 역분산 가중 최소 제곱 추정치는 선형 편향 추정치가 가장 좋습니다. 그러나 조건부 분산은 거의 알려져 있지 않습니다. 따라서 MME를 풀 때 분산과 가중 모수 추정치를 공동으로 추정하는 것이 바람직합니다.

이러한 혼합 모델을 맞추기 위해 사용되는 한 가지 방법은 분산 구성 요소가 결합 가능성에서 관찰되지 않은 성가신 매개 변수로 처리되는 기대-최대화 알고리즘(EM)의 방법입니다.^[18] 현재 이는 Python(stats models package), SAS(proc mixed)와 같은 통계 소프트웨어에서 구현되는 방법이며, R의 nlme package lme()에서만 초기 단계로 구현됩니다. 혼합 모형 방정식의 해는 오차 분포가 정규 분포일 때 최대 우도 추정치입니다.^[19]^[20]

선형 회귀 모형에는 고정 효과, 혼합 효과 및 랜덤 효과가 영향을 미칩니다.

${\boldsymbol {u}}$ 모델을 맞추는 방법에는 처음에 MEM을 사용하는 방법을 비롯하여 여러 가지가 있습니다. 그런 다음 뉴턴-랩슨^[21](R 패키지 nlme의 lme()에서 사용)은 u {\ $displaystyle$ 의 (저차원) 분산 공분산 매개변수에 따라서만 프로파일 로그 가능성을 얻기 위해 최소 제곱에 불이익을 주었습니다 ${\boldsymbol {u}}$ 즉, cov 매트릭스 ${\boldsymbol {G}}$ ${\$ 그리고 감소된 목적 함수에 대한 현대적인 직접 최적화(R의 lme4^[22] 패키지 lmer() 및 Julia 패키지 MixedModels.jl에서 사용), 가능성에 대한 직접 최적화(예: 사용). R's glmmTMB). 특히 Henderson이 제안한 표준 형식은 이론에 유용하지만 많은 인기 소프트웨어 패키지는 희소 행렬 방법(예: lme4 및 MixedModels.jl)을 활용하기 위해 수치 계산에 다른 공식을 사용합니다.

참고 항목

참고문헌

^ Baltagi, Badi H. (2008). Econometric Analysis of Panel Data (Fourth ed.). New York: Wiley. pp. 54–55. ISBN 978-0-470-51886-1.
^ ^a ^b Gomes, Dylan G.E. (20 January 2022). "Should I use fixed effects or random effects when I have fewer than five levels of a grouping factor in a mixed-effects model?". PeerJ. 10: e12794. doi:10.7717/peerj.12794. PMC 8784019. PMID 35116198.
^ Yang, Jian; Zaitlen, NA; Goddard, ME; Visscher, PM; Prince, AL (29 January 2014). "Advantages and pitfalls in the application of mixed-model association methods". Nat Genet. 46 (2): 100–106. doi:10.1038/ng.2876. PMC 3989144. PMID 24473328.
^ ^a ^b Seltman, Howard (2016). Experimental Design and Analysis. Vol. 1. pp. 357–378.
^ ^a ^b "Introduction to Linear Mixed Models". Advanced Research Computing Statistical Methods and Data Analytics. UCLA Statistical Consulting Group. 2021.
^ ^a ^b Kreft & de Leeuw, J. Introducing multilevel modeling. London:Sage.
^ ^a ^b Raudenbush,Bryk, S.W,A.S (2002). Hierarchical Linear Models: Applications and Data Analysis Methods. Thousand Oaks,CA: Sage.{{cite book}}: CS1 maint: 다중 이름: 저자 목록 (링크)
^ ^a ^b Snijders,Bosker, T.A.B, R.J (2012). Multilevel analysis: An introduction to basic and advanced multilevel modeling. Vol. 2nd edition. London:Sage.{{cite book}}: CS1 maint: 다중 이름: 저자 목록 (링크)
^ Fisher, RA (1918). "The correlation between relatives on the supposition of Mendelian inheritance". Transactions of the Royal Society of Edinburgh. 52 (2): 399–433. doi:10.1017/S0080456800012163. S2CID 181213898.
^ ^a ^b Robinson, G.K. (1991). "That BLUP is a Good Thing: The Estimation of Random Effects". Statistical Science. 6 (1): 15–32. doi:10.1214/ss/1177011926. JSTOR 2245695.
^ C. R. Henderson; Oscar Kempthorne; S. R. Searle; C. M. von Krosigk (1959). "The Estimation of Environmental and Genetic Trends from Records Subject to Culling". Biometrics. International Biometric Society. 15 (2): 192–218. doi:10.2307/2527669. JSTOR 2527669.
^ ^a ^b L. Dale Van Vleck. "Charles Roy Henderson, April 1, 1911 – March 14, 1989" (PDF). United States National Academy of Sciences.
^ McLean, Robert A.; Sanders, William L.; Stroup, Walter W. (1991). "A Unified Approach to Mixed Linear Models". The American Statistician. American Statistical Association. 45 (1): 54–64. doi:10.2307/2685241. JSTOR 2685241.
^ Anderson, R.J (2016). ""MLB analytics guru who could be the next Nate Silver has a revolutionary new stat"".
^ Obenchain,Lilly, Bob,Eli (1993). "Data Analysis and Infromation Visualization" (PDF). MWSUG.{{cite book}}: CS1 maint: 다중 이름: 저자 목록 (링크)
^ Chen, H; Wang, C; Conomos, MP; Stilp, AM; Li, Z; Sofer, T; Szpiro, AA; Chen, W; Brehm, JM; Celedon, JC; Redline, S; Papanicolaou, S; Thorton, GJ; Thorton, TA; Laurie, CC; Rice, K; Lin, X (7 April 2016). "Control for Population Structure and Relatedness for Binary Traits in Genetic Association Studies via Logistic Mixed Models". AM J Hum Genet. 98 (4): 653–666. doi:10.1016/j.ajhg.2016.02.012. PMC 4833218. PMID 27018471.
^ Henderson, C R (1973). "Sire evaluation and genetic trends" (PDF). Journal of Animal Science. American Society of Animal Science. 1973: 10–41. doi:10.1093/ansci/1973.Symposium.10. Retrieved 17 August 2014.
^ Lindstrom, ML; Bates, DM (1988). "Newton–Raphson and EM algorithms for linear mixed-effects models for repeated-measures data". Journal of the American Statistical Association. 83 (404): 1014–1021. doi:10.1080/01621459.1988.10478693.
^ Laird, Nan M.; Ware, James H. (1982). "Random-Effects Models for Longitudinal Data". Biometrics. International Biometric Society. 38 (4): 963–974. doi:10.2307/2529876. JSTOR 2529876. PMID 7168798.
^ Fitzmaurice, Garrett M.; Laird, Nan M.; Ware, James H. (2004). Applied Longitudinal Analysis. John Wiley & Sons. pp. 326–328.
^ Pinheiro, J; Bates, DM (2006). Mixed-effects models in S and S-PLUS. Statistics and Computing. New York: Springer Science & Business Media. doi:10.1007/b98882. ISBN 0-387-98957-9.
^ Bates, D.; Maechler, M.; Bolker, B.; Walker, S. (2015). "Fitting Linear Mixed-Effects Models Using lme4". Journal of Statistical Software. 67 (1). doi:10.18637/jss.v067.i01.

Search