등방성 회귀
Isotonic regression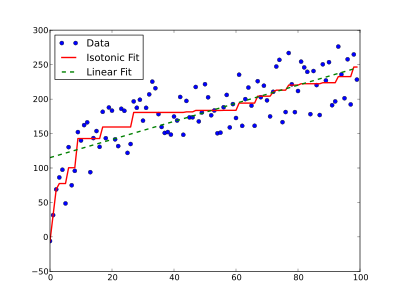
| 시리즈의 일부 |
| 회귀 분석 |
|---|
| 모델 |
| 견적 |
| 배경 |
통계 및 수치 분석에서 등각 회귀 또는 단조 회귀는 자유 형태의 선을 일련의 관측치에 적합시켜 적합선이 어디에서나 감소하지 않고(또는 증가하지 않음) 관측치에 가능한 한 가깝게 배치하는 기법입니다.
적용들
등방성 회귀는 통계적 추론에 적용된다.예를 들어 특정 순서에 따라 평균이 증가할 것으로 예상되는 경우 등각 곡선을 사용하여 실험 결과의 평균에 적합시킬 수 있습니다.등방성 회귀의 장점은 함수가 단조롭게 증가하는 한 선형 회귀에 의해 부과되는 선형성 등 어떤 함수 형태에도 구속되지 않는다는 것입니다.
또 다른 어플리케이션은 비메트릭 다차원 스케일링이며,[1] 여기서 데이터 포인트의 저차원적인 임베딩이 요구되며, 임베딩 내의 포인트 간의 거리 순서가 포인트 간의 차이 순서에 일치한다.동위원소 회귀는 이상적인 거리를 맞추기 위해 반복적으로 사용되어 상대적 차이점 순서를 유지합니다.
동위원소 회귀는 또한 감독된 기계 학습 [2]모델의 예측 확률을 보정하기 위해 확률론적 분류에 사용된다.
x x의 단순 주문 사례에 대한 등방성 회귀는 마취학 및 독성학 등의 분야에서 연속 용량-반응 관계를 추정하는 데 적용되었다.좁게 말하면, 등방성 회귀는의 관측값에서만 점 추정치를 제공한다 \\ x 추가 가정 없이 완전한 선량-반응 곡선의 추정은 보통 점 추정치 사이의 선형 보간을 통해 이루어진다.[3]
R,[4][5][6] Stata 및 [7]Python용으로 아이소톤(단조) 회귀 계산 소프트웨어가 개발되었습니다.
문제 설명 및 알고리즘
,1) , , ( , n { (_ {, \, ( x { , _ { n ) } 。서 y R \ \ \ { R i i i i x _ { { R in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in in일반성의 각 관측치 {에는 가 될 수 있습니다. 단, 으로 wi { 은 모든 i { i}에 대해 가 됩니다
등각 회귀는 에 y i y y i y y y ^ y y y y j y j y j^ style \ { { }} q i yfor y } y y _ { i} } } q q q q q q q q q q q q q q q q q q q q q q q q q q q q q를 통해 변수 y,…,y {1},\ldotsn}}에 다음 2차 프로그램(QP)이 표시됩니다.
- i n i ( ^ - ) \ _ { i=} { n} w { }( { \{ - _ { } { } ^ ∈ ∈∈ ∈ ∈ hat hat hat hat hat hat hat hat hat hat hat hat hat hat hat hat hat hat hat hat hat hat
서 E { ( ,) : i j { E = \ { ( , ) : x{ } \ x { } } ( ) displaydisplay 、 displaydisplaydisplaydisplaydisplaydisplaydisplay1 displaydisplaydisplaydisplaydisplay1display1displaydisplay1 display1 displaydisplay1 display1 displaydisplaydisplay1 display1 display1 display1 displaydisplay1 display1 display이 형식의 문제는 일반 2차 프로그래밍 기법으로 해결할 수 있다.
i 이 R과 완전히 순서가 매겨진 집합인 일반적인 설정에서는 WLOG가 1 x \ x{ 1 _ } \ x cd } \ cd \ cd \ cd \ cdots \ cdots le \ cdots } \ ltsets le \ lts q le q q q q: < { E = \ { ( , +) : \ i < \}. 이 경우 2차 프로그램을 해결하기 위한 간단한 반복 알고리즘은 인접한 풀 위반자 알고리즘입니다반대로, Best와 Chakravarti는[8] 이 문제를 활성 집합 식별 문제로 연구하여 원시 알고리즘을 제안했다.이 두 알고리즘은 서로 이중으로 볼 수 있으며, 이미 정렬된 [8]데이터에 대한 계산 복잡도는 모두 OO()이다.
동위원소 회귀 작업을 완료하기 위해 fi i \ i})와 같은 함수 f 를 선택할 수 있습니다. i에 대해 i}개 모자.이러한 기능을 사용하면
- f n i( ( i ) - y i ) \ _ { } \ { i } { n _ { i } w { } ( ( _ { ) - _ { i }^2}}f { f}는 해제되지 .
및의 새로운 값에 대한yx) 을 예측하기 위해 사용할 수 있습니다. iR (\ )의 인 선택은 과 같이 i , ^) \},\hat { {y}} {}}} {i {i {i}}}의 점 사이에 직선적으로 보간삽삽삽삽하는 것입니다.연속적인 부분 선형 함수를 생성하는 경우:
중심 등방성 회귀 분석
이 기사의 첫 번째 그림에서 보듯이, 단조성 위반이 있는 경우 결과 보간 곡선은 평평한(일정) 간격을 가집니다.용량-응답 애플리케이션에서는 일반적으로 f() { f가 단조일 뿐만 아니라 매끄러운 것으로 있습니다.플랫 인터벌은 f() { f의 가정된 형상과 되지 않으며 편향된 것으로 나타날 수 있습니다.중심 등방성 회귀(CIR)라는 이름의 그러한 애플리케이션에 대한 간단한 개선은 Oron과 Flownoy에 의해 개발되었으며 선량-반응 [9]및 선량-검색 애플리케이션 모두에 대한 추정 오류를 상당히 감소시키는 것으로 나타났다.일변량에 대한 CIR 및 표준 등방성 회귀 분석(단순한 경우)은 모두 R 패키지 "cir"[4]로 구현됩니다.이 패키지는 또한 분석적 신뢰 구간 추정치를 제공한다.
레퍼런스
- ^ Kruskal, J. B. (1964). "Nonmetric Multidimensional Scaling: A numerical method". Psychometrika. 29 (2): 115–129. doi:10.1007/BF02289694.
- ^ "Predicting good probabilities with supervised learning Proceedings of the 22nd international conference on Machine learning". dl.acm.org. doi:10.1145/1102351.1102430. Retrieved 2020-07-07.
- ^ Stylianou, MP; Flournoy, N (2002). "Dose finding using the biased coin up-and-down design and isotonic regression". Biometrics. 58 (1): 171–177. doi:10.1111/j.0006-341x.2002.00171.x. PMID 11890313.
- ^ a b Oron, Assaf. "Package 'cir'". CRAN. R Foundation for Statistical Computing. Retrieved 26 December 2020.
- ^ Leeuw, Jan de; Hornik, Kurt; Mair, Patrick (2009). "Isotone Optimization in R: Pool-Adjacent-Violators Algorithm (PAVA) and Active Set Methods". Journal of Statistical Software. 32 (5): 1–24. doi:10.18637/jss.v032.i05. ISSN 1548-7660.
- ^ Xu, Zhipeng; Sun, Chenkai; Karunakaran, Aman. "Package UniIsoRegression" (PDF). CRAN. R Foundation for Statistical Computing. Retrieved 29 October 2021.
- ^ Pedregosa, Fabian; et al. (2011). "Scikit-learn:Machine learning in Python". Journal of Machine Learning Research. 12: 2825–2830. arXiv:1201.0490. Bibcode:2012arXiv1201.0490P.
- ^ a b Best, Michael J.; Chakravarti, Nilotpal (1990). "Active set algorithms for isotonic regression; A unifying framework". Mathematical Programming. 47 (1–3): 425–439. doi:10.1007/bf01580873. ISSN 0025-5610.
- ^ Oron, AP; Flournoy, N (2017). "Centered Isotonic Regression: Point and Interval Estimation for Dose-Response Studies". Statistics in Biopharmaceutical Research. 9 (3): 258–267. arXiv:1701.05964. doi:10.1080/19466315.2017.1286256.
추가 정보
- Robertson, T.; Wright, F. T.; Dykstra, R. L. (1988). Order restricted statistical inference. New York: Wiley. ISBN 978-0-471-91787-8.
- Barlow, R. E.; Bartholomew, D. J.; Bremner, J. M.; Brunk, H. D. (1972). Statistical inference under order restrictions; the theory and application of isotonic regression. New York: Wiley. ISBN 978-0-471-04970-8.
- Shively, T.S., Sager, T.W., Walker, S.G. (2009). "A Bayesian approach to non-parametric monotone function estimation". Journal of the Royal Statistical Society, Series B. 71 (1): 159–175. CiteSeerX 10.1.1.338.3846. doi:10.1111/j.1467-9868.2008.00677.x.
{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크) - Wu, W. B.; Woodroofe, M.; Mentz, G. (2001). "Isotonic regression: Another look at the changepoint problem". Biometrika. 88 (3): 793–804. doi:10.1093/biomet/88.3.793.
 단순 주문 사례에 대한 등방성 회귀는 마취학 및 독성학 등의 분야에서 연속 용량-반응 관계를 추정하는 데 적용되었다.좁게 말하면, 등방성 회귀는
단순 주문 사례에 대한 등방성 회귀는 마취학 및 독성학 등의 분야에서 연속 용량-반응 관계를 추정하는 데 적용되었다.좁게 말하면, 등방성 회귀는
















 같은
같은 



 예측하기 위해 사용할 수 있습니다.
예측하기 위해 사용할 수 있습니다. 



