순환군

대수구조 → 군론 군론
기본 개념 서브그룹 정규 부분군 몫군 (반쪽-)다이렉트 프로덕트 군 동형사상 커널 이미지 직접 합계 화환 제품 간단하죠. 유한한 인피니트 계속되는 곱셈의 첨가물 순환의 아벨리안 이면체 무효 해결 가능한 액션. 군론 용어집 그룹 이론 토픽 목록
유한군 유한단순군분류 순환의 번갈아 거짓말형 산발적인 코시의 정리 라그랑주 정리 시로우 정리 홀의 정리 p그룹 초등 아벨 군 프로베니우스군 슈어 승수 대칭군n S 클라인 4족 V 이면체군n D 사분위수 Q 쌍환기n Dic
개별 그룹 격자 ${\displaystyle \mathbb{}}$($$Z \$displaystyle \mathbb {Z$$$) 자유 그룹 모듈러 그룹 PSL(2,$Z{\displaystyle \mathbb{}}$ \$style \mathbb {Z$ 표시$)$ SL(2,$Z{\displaystyle \mathbb{}}$ \$displaystyle \mathbb {Z$ 산술군 격자 쌍곡선 군
토폴로지 그룹 및 Lie 그룹 솔레노이드 원형 일반 선형 GL(n) 특수 선형 SL(n) 직교 O(n) 유클리드 E(n) 특수 직교 SO(n) 유니터리 U(n) 특수 유니터리 SU(n) 심플렉틱 Sp(n) G2 에프4 E6. E7. E8. 로렌츠 푸앵카레 컨포멀 미분 동형 고리 무한 차원 리 군 O()) SU()) Sp())
대수군 선형 대수군 환원군 아벨 변종 타원 곡선
v t

군 이론에서, 추상 대수학, 순환군 또는 단성군은 단일 ^[1]원소에 의해 생성되는 군이다.즉, 단일 연관 이진 연산을 갖는 반전 요소 집합이며 g 또는 그 역연산을 반복하여 그룹의 다른 모든 요소를 얻을 수 있도록 요소 g를 포함합니다.각 원소는 곱셈표기법에서는 g의 거듭제곱으로, 가법표기법에서는 g의 배수로서 쓸 수 있다.이 요소 g를 그룹의 ^[1]생성기라고 합니다.

모든 무한 순환군은 Z의 가법군인 정수군과 동형이다.차수 n의 모든 유한 순환군은 정수 모듈로 n인 Z/nZ의 가법군과 동형이다.모든 순환군은 아벨군이고(그들의 군 연산이 가환적이라는 것을 의미), 그리고 모든 최종 생성된 아벨군은 순환군의 직접적인 산물이다.

모든 소수 순환 그룹은 단순한 그룹으로, 더 작은 그룹으로 나눌 수 없습니다.유한 단순 그룹의 분류에서, 세 개의 무한 클래스 중 하나는 소수의 순환 그룹으로 구성됩니다.따라서 주순서 순환 그룹은 모든 그룹을 만들 수 있는 구성 요소 중 하나입니다.

정의 및 표기법

임의의^k 그룹 G의 원소 g에 대해, g에 의해 생성된 순환 부분군이라고 불리는 모든 정수 거듭제곱으로 구성된 부분군을 형성할 수 있다.g의 순서는 g의 원소수입니다.즉, 요소의 순서는 생성되는 순환 서브그룹의 순서와 동일합니다.

순환 그룹은 순환 부분군 중 하나와 동일한 그룹입니다. G의 발생기라고 불리는 일부 요소 g에 대해 G = µg입니다.

순서 n의 유한 순환군 G에 대해 G = {e, g, g², ..., gⁿ⁻¹}을 가진다. 여기서 e는 항등 원소이고ⁱ g = g는^j i µ j(mod n), 특히 gⁿ = g⁰ = e, g⁻¹ = g이다ⁿ⁻¹.이 곱셈에 의해 정의된 추상군은 종종 C로 표시되며_n, 우리는 G가 표준 순환군_n C와 동형이라고 말한다.이러한 그룹은 덧셈 연산을 갖는 정수 모듈로 n의 군인 Z/nZ와도 동형이며, 이는 가법 표기법의 표준 순환 군이다.θ(gⁱ) = i로 정의되는 동형사상 θ에서 항등원소 e는 0에 해당하고 곱은 합계에 해당하며, 거듭제곱은 배수에 해당한다.

예를 들어, 복잡한 통합의 6번째 루트 집합은

는 곱셈 아래에 그룹을 형성합니다.때문에 그 원시적인 뿌리 z에 의해 만들어진다 이건, 음 12+32나는 e2π 나는/6:{\displaystyle z={\tfrac{1}{2}}+{\tfrac{\sqrt{3}}{2}}i=e^{2\pi i/6}원:}그것은, G=⟨z⟩)z6과{1, z, 다음, z3, z4, z5})1. 편지의 변화에 따르면, 이 표준 순회 군(구조적으로는 같은)에 동형은 o. 순환은위해서der 6, 곱셈^j g · g^k = g^{j+k(mod 6)} = g의 C = g = { e, g, g²³, g⁴, g⁵ }로₆ 정의되므로 g = g⁰ = e가 된다⁶.이 군들은 또한 z와^k g가 k에 대응하며^k, 덧셈 모듈로 6의 연산으로 Z/6Z = {0, 1, 2, 3, 4, 5}과 동형이다.예를 들어, 1 + 2 ( 3 (mod 6)은¹ z² · z³ = z에 해당하고, 2 + 5 ( 1 (mod 6)은⁵⁷ z · z = z에¹ 해당된다².모든 원소는 자체 순환 서브그룹을 생성하는데, 예를 들어 δz² = C 및 Z/3Z와₃ 동형이며, δz⁵ = {e⁵¹⁰, z²⁴, z⁴¹⁵ = z³²⁰ = z²²⁵ = z = z = G이며, z 차수 6을 가지며⁵ G의 대체 생성기이다.

몫 표기법 Z/nZ, Z/(n) 또는 Z/n 대신, 일부 저자들은 유한 순환군을_n Z로 나타내지만, 이것은_p 숫자 이론의 표기법, 즉 Z가 p-adic 숫자 고리 또는 소수 이상에서의 국재화와 상충된다.

무한 순환군

p1, (*syslog)	p11g, (22인치)
두 개의 프리즈 그룹은 Z와 동형이다.1개의 제너레이터로 p1에는 변환이 있고 p11g에는 활공반사가 있습니다.

한편, 무한 순환군 G = δg에서, 거듭제곱^k g는 모든 정수 k에 대해 구별되는 요소를 부여하므로, G = {..., g⁻², g⁻¹, e, g, g², ...}, G는 표준군 C = C_∞ 및 정수의 가법군 Z와 동형이다.예를 들어 첫 번째 프리즈 그룹이 있습니다.여기에는 유한한 주기가 없으며, "순환"이라는 이름은 ^[2]오해를 불러일으킬 수 있습니다.

이러한 혼동을 피하기 위해 부르바키는 단일 생성기를 가진 그룹에 대해 단일 그룹이라는 용어를 도입했고 "순환 그룹"은 유한 단일 그룹을 의미하도록 제한하여 "무한 순환 그룹"^{[note 1]}이라는 용어를 피했다.

예

회전 대칭의 순환 그룹 예제

C1.	C2.	C3.
C4.	C5.	C6.

정수 및 모듈러 추가

정수 집합 Z는 덧셈 연산을 통해 ^[1]그룹을 형성합니다.모든 정수는 단일 숫자 1을 더하거나 빼서 쓸 수 있기 때문에 무한 순환군이다.이 그룹에서는 1과 -1만이 제너레이터입니다.모든 무한 순환군은 Z와 동형이다.

모든 양의 정수 n에 대해, 다시 덧셈 연산에 의해, 일련의 정수 modulo n은 Z/^[1]nZ라고 하는 유한 순환군을 형성한다.모듈러 정수 i는 i가 상대적으로 소수인 경우 이 그룹의 생성기이며, 이러한 요소들은 정수 덧셈을 통해 그룹의 다른 모든 요소를 생성할 수 있기 때문입니다.(이러한 생성기의 수는 θ(n)이며, 여기서 θ는 오일러 전체 함수이다.)모든 유한 순환군 G는 Z/nZ와 동형이며, 여기서 n = G는 그룹의 순서이다.

순환 그룹을 정의하는 데 사용되는 정수 및 모듈러 정수에 대한 덧셈 연산은 교환환의 덧셈 연산으로, Z 및 Z/nZ 또는 Z/(n)로도 표시됩니다.p가 소수일 경우 Z/pZ는 유한 필드이며, 일반적으로 갈로아 필드의 경우 F 또는 GF(p)로_p 표시됩니다.

모듈러 곱셈

각 양의 정수 n에 대해 n에 대해 상대적으로 소수인 정수 모듈로 n의 집합을 (Z/nZ)^×로 하여 곱셈 연산 하에 군을 형성한다.이 그룹은 항상 순환적인 것은 아니지만, n이 홀수 소수의 거듭제곱 또는 홀수 소수의 2배(^[4][5]OEIS의 시퀀스 A033948)인 경우 항상 순환적입니다.이것은 고리 Z/nZ의 단위들의 곱셈군이다; 그것들 중 θ(n)가 있고, 여기서 θ는 오일러 전체 함수이다.예를 들어, (Z/6Z)^× = {1, 5}이며, 6은 홀수 소수의 두 배이므로 순환군입니다.반대로, (Z/8Z)^× = {1, 3, 5, 7}은 클라인 4-군이며 순환이 아니다.(Z/nZ)^×가 순환일 때, 그 발생기를 원시근 모듈로 n이라고 합니다.

소수 p의 경우, 그룹(Z/pZ)^×은 항상 순환이며, 순서 p의 유한 필드의 0이 아닌 원소로 구성됩니다.보다 일반적으로, 모든 필드의 곱셈 그룹의 모든 유한 부분군은 ^[6]순환적입니다.

회전 대칭

폴리곤의 회전 대칭 집합은 유한 순환 ^[7]그룹을 형성합니다.회전(늘 회전 포함)으로 폴리곤을 스스로 이동하는 방법이 n개 있는 경우 이 대칭 그룹은 Z/nZ와 동형입니다.3차원 또는 그 이상의 차원에는 순환적인 다른 유한 대칭 그룹이 존재하지만, 모든 것이 축을 중심으로 회전하는 것이 아니라 회전하는 것입니다.

원¹ S(원 그룹, S로도 표시됨)의 모든 회전 그룹은¹ 순환이 아닙니다. 정수 거듭제곱이 모든 회전을 발생시키는 단일 회전은 없기 때문입니다.사실 무한 순환군_∞ C는 셀 수 있지만¹ S는 셀 수 없습니다.합리적인 각도에 의한 회전 그룹은 셀 수 있지만 여전히 순환적이지는 않습니다.

갈로아 이론

단일성의 n번째 루트는 n번째 거듭제곱이 1인 복소수이며, 이는 다항식ⁿ x - 1의 루트이다.단일성의 모든 n번째 루트 집합은 ^[1]곱셈에서 순서 n의 순환 그룹을 형성한다.예를 들어, 다항식³ z - 1 인자는 (z - 1)(z - ))(z² - ))이며, 여기서 ω^2πi/32 = e, 집합 {1, ,, }} = {,, ,}은⁰¹² 곱셈 하에서 순환군을 형성한다.통합의 n번째 근에 의해 생성된 유리수의 필드 확장의 갈루아 그룹은 순서 θ(n)의 곱셈군(Z/nZ)^×과 동형인 다른 그룹을 형성하며, 이는 전체 n이 아닌 일부에 대해 주기적이다(위 참조).

필드 확장은 Galois 그룹이 주기적인 경우 주기 확장이라고 불립니다.특성 0의 장에 대해, 그러한 확장은 쿠머 이론의 주제이며, 라디칼에 의한 용해성과 밀접하게 관련되어 있다.특성 p의 유한장을 확장하기 위해, 그 갈로아 그룹은 항상 유한하고 순환적이며, 프로베니우스 ^[8]매핑의 거듭제곱에 의해 생성된다.반대로 유한장 F와 유한순환군 G가 주어졌을 때, 갈로아군이 ^[9]G인 F의 유한장 확장이 존재한다.

서브그룹

순환 그룹의 모든 부분군 및 몫 그룹은 주기적입니다.구체적으로, Z의 모든 부분군은 µm = mZ이며, m은 양의 정수이다.이러한 모든 부분군은 서로 구별되며, 사소한 그룹 {0} = 0Z를 제외하고 모두 Z와 동형이다.Z의 부분군 격자는 ^[10]나눗셈으로 정렬된 자연수 격자의 쌍대와 동형입니다.따라서 소수 p는 약수가 아니기 때문에 pZ는 최대 고유 부분군이며, 몫군 Z/pZ는 단순하다. 사실 순환군은 그 순서가 ^[11]소수일 경우에만 단순하다.

Z/0Z = Z/{0}을(를) 제외하고 모든 몫 그룹 Z/nZ는 유한합니다.몫군 Z/nZ는 n의 양의 제수 d마다 n/d의 잔차 클래스에 의해 생성되는 순서 d의 서브그룹을 정확하게 가진다.다른 부분군은 없습니다.

기타 속성

모든 순환군은 아벨 ^[1]군이다.즉, gh = hg(G의 모든 g와 h에 대하여)의 가환 연산입니다.이는 r + s µ s + r (mod n) 이후의 정수 및 모듈러 덧셈 그룹에 대해 명확하며, 모든 순환 그룹에 대해 이러한 표준 그룹과 모두 동일하기 때문에 그 결과가 뒤따른다.순서 n의 유한한 순환군에 대해ⁿ g는 임의의 요소 g의 항등요소이다.모든 정수 k에 대해 kn ( 0 (mod n)이므로, 이것은 모듈러 덧셈에 대한 동형사상을 다시 사용한다. (이것은 라그랑주의 정리에 의한 일반적인 순서 n의 그룹에도 해당된다.)

소수^k p의 경우, Z/pZ^k 그룹은 1차 순환군이라고 불립니다.아벨 군들의 기본 정리는 모든 최종 생성된 아벨 군들은 일차 순환 군과 무한 순환 군들의 유한한 직접적 산물이라고 말한다.

순환군은 아벨 군이기 때문에 각각의 켤레 클래스는 단일 원소로 구성됩니다.따라서 순서 n의 순환군은 n개의 켤레 클래스를 가진다.

d가 n의 제수일 경우, Z/nZ에서 d순서를 갖는 원소의 수는 θ(d)이고, d순서를 나누는 원소의 수는 정확히 d이다.만약 G가 각 n > 0에 대해 G가 n을 나누는 최대 n개의 원소를 포함하는 유한군이라면, G는 ^{[note 2]}순환적이어야 한다.Z/nZ에서의 요소 m의 순서는 n/gcd(n,m)입니다.

n과 m이 공역일 경우, 2개의 순환군 Z/nZ와 Z/mZ의 직접곱은 순환군 Z/nmZ와 동형이며, 그 반대의 경우도 성립한다: 이것은 중국어 나머지 정리의 한 형태이다.예를 들어 Z/12Z는 동형사상(k mod 12) → (k mod 3, k mod 4) 하에서는 직곱 Z/3Z × Z/4Z와 동형사상이지만, 각 원소가 최대 6을 갖는 Z/6Z × Z/2Z와는 동형이 아니다.

p가 소수일 경우, p 원소를 가진 군들은 단순 군 Z/pZ와 동형이다.숫자 n은 Z/nZ가 순서 n의 유일한 그룹인 경우 순환수라고 불리며, 이는 gcd(n, δ(n) = ^[13]1일 때 정확히 참이다. 순환수는 모든 소수를 포함하지만, 일부는 15와 같이 복합적이다.그러나 2를 제외한 모든 순환 숫자는 홀수입니다.순환 번호는 다음과 같습니다.

1, 2, 3, 5, 7, 13, 15, 17, 19, 23, 29, 31, 33, 35, 37, 43, 47, 51, 53, 59, 61, 65, 67, 69, 71, 77, 79, 83, 83, 87, 89, 91, 95, 97, 101, 107, 107, 107, 113, 115, 115, 133, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 137, 139

이 정의는 순환 그룹이 유한 ^[14]n에 대해 그룹_∞ 표현 C = ⟩x and_n 및 C = ⟩xⁿ x for를 갖는다는 것을 즉시 암시한다.

연관된 오브젝트

표현

순환군의 표현 이론은 보다 일반적인 유한군의 표현 이론의 중요한 기본 사례이다.복합적인 경우, 순환군의 표현은 직선 문자의 직합으로 분해되어, 문자 이론과 표현 이론의 관계를 투명하게 한다.긍정적 특징의 경우, 순환 그룹의 분해 불가능한 표현은 순환 시로우 서브그룹을 가진 그룹의 표현 이론과 보다 일반적으로 순환 결함 블록의 표현 이론을 위한 모델 및 귀납적 기초를 형성한다.

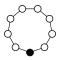
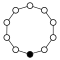
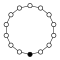
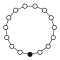
순환 그래프

사이클 그래프는 그룹의 다양한 사이클을 나타내며 특히 작은 유한 그룹의 구조를 시각화하는 데 유용합니다.순환 그룹의 주기 그래프는 단순히 원형 그래프이며, 여기서 그룹 순서는 노드 수와 같다.단일 제너레이터는 그룹을 그래프상의 방향 경로로 정의하고 역방향 제너레이터는 역방향 경로를 정의합니다.일반 경로(아이덴티티)는 루프로 그릴 수 있지만 일반적으로 억제됩니다.Z는₂ 다중 그래프로 두 개의 곡선 ^[15]모서리를 사용하여 그려지는 경우가 있습니다.

순환군_n Z는 n차수를 가지며, 원소를 정점에 두고 n변 폴리곤으로서 단순하게 그래프로 나타낸 단일 사이클에 대응한다.

순서 24까지 그래프를 순환합니다.

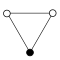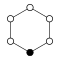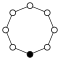Z1	Z2	Z3	Z4	Z5	Z6 = Z3×Z2	Z7	Z8
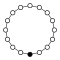Z9	Z10 = Z5×Z2	Z11	Z12 = Z4×Z3	Z13	Z14 = Z7×Z2	Z15 = Z5×Z3	Z16
Z17	Z18 = Z9×Z2	Z19	Z20 = Z5×Z4	Z21 = Z7×Z3	Z22 = Z11×Z2	Z23	Z24 = Z8×Z3

케일리 그래프

케일리 그래프는 쌍(G, S)에서 정의된 그래프이며, 여기서 G는 그룹이고 S는 그룹의 생성기 세트입니다. 각 그룹 요소에 대한 정점과 생성기를 가진 요소의 각 곱에 대한 엣지가 있습니다.유한 순환 그룹의 경우, 단일 생성기를 가진 케일리 그래프는 주기 그래프이며, 생성기를 가진 무한 순환 그룹의 경우 케일리 그래프는 이중 무한 경로 그래프이다.그러나 케일리 그래프는 다른 생성기 집합에서도 정의할 수 있다.임의 생성기 세트가 있는 순환 그룹의 케일리 그래프를 순환 ^[16]그래프라고 합니다.이러한 그래프는 각 점이 다른 점과 동일한 거리 세트를 가진 인접점에 연결된 상태에서 원이나 선에서 등간격 점 집합으로 기하학적으로 표현될 수 있습니다.대칭 그룹이 전이 순환 ^[17]그룹을 포함하는 정점 전이 그래프입니다.

내형사상

아벨 군 Z/nZ의 내형성 고리는 ^[18]고리로서의 Z/nZ 자체와 동형이다.이 동형사상 하에서, 숫자 r은 각 요소를 그것의 r개의 복사본의 합에 매핑하는 Z/nZ의 내형사상에 대응한다.이는 r이 n과 공명하는 경우에만 분사가 되므로 Z/nZ의 자기동형군은 단위군(Z/nZ)^×[18]과 동형이다.

마찬가지로 Z의 가법군의 내형 고리는 고리 Z와 동형이다.그 자기동형군은 고리 Z의 단위군({-1, +1}, ×) c₂ C와 동형이다.

그룹의 관련 클래스

다른 여러 그룹의 클래스는 순환 그룹과의 관계에 의해 정의되었다.

가상 순환 그룹

유한 지수(부분군이 갖는 코세트 수)의 순환 부분군을 포함하는 그룹을 사실상 순환 그룹이라고 합니다.즉, 순환 서브그룹의 멤버와 특정 유한 집합의 멤버를 곱함으로써 가상순환군 내의 임의의 원소에 도달할 수 있다.모든 순환군은 모든 유한군과 마찬가지로 사실상 순환군이다.무한군은 최종적으로 생성되고 정확히 두 개의 ^{[note 3]}끝을 갖는 경우에만 사실상 순환적이다. 이러한 그룹의 예는 Z/nZ와 Z의 직접곱이며, 여기서 인자 Z는 유한 지수 n을 가진다.그로모프 쌍곡선 그룹의 모든 아벨 부분군은 사실상 ^[20]주기적이다.

로컬 순환 그룹

국소 순환 그룹은 완전히 생성된 각 부분군이 순환적인 그룹입니다.예를 들어 유리수의 가법군은 다음과 같습니다. 유리수의 모든 유한 집합은 단일 단위 분수의 정수 배수 집합이며, 가장 낮은 공통 분모의 역수이며, 부분군으로서 이 단위 분수의 정수 배수들의 순환 그룹을 생성합니다.부분군의 격자가 분포 ^[21]격자인 경우에만 그룹은 로컬 순환입니다.

순환 순서 그룹

순환순서군은 그룹구조에 의해 보존된 순환순서와 함께 그룹이다.모든 순환 그룹은 정수의 순서(또는 그룹의 순서)와 일치하는 순환 순서 그룹으로 구조가 주어질 수 있습니다.순환 순서 그룹의 모든 유한 부분군은 ^[22]순환이다.

메타사이클릭 및 다환기

메타사이클릭 그룹은 비율도 ^[23]순환인 순환 정규 부분군을 포함하는 그룹입니다.이러한 그룹에는 순환 그룹, 쌍환 그룹 및 두 개의 순환 그룹의 직접 산물이 포함됩니다.다환 그룹은 하나 이상의 그룹 확장을 허용함으로써 메타환 그룹을 일반화한다.그룹은 유한 내림차순의 부분군을 가지며, 각각은 순환상수를 갖는 이전 부분군에서 정규적이며, 사소한 그룹으로 끝나는 경우 다환식이다.완전히 생성된 모든 아벨 군 또는 제로 가성군은 ^[24]다환식이다.

「 」를 참조해 주세요.

• 순환 그래프(그룹)
• 순환 모듈
• 순환 체질
• 프뤼퍼 군(계산 가능한 무한 아날로그)
• 원군(무한 아날로그)

각주

메모들

인용문

레퍼런스

• Alonso, J. M.; et al. (1991), "Notes on word hyperbolic groups", Group theory from a geometrical viewpoint (Trieste, 1990) (PDF), River Edge, NJ: World Scientific, Corollary 3.6, MR 1170363, archived from the original (PDF) on 2013-04-25, retrieved 2013-11-26
• Alspach, Brian (1997), "Isomorphism and Cayley graphs on abelian groups", Graph symmetry (Montreal, PQ, 1996), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., vol. 497, Dordrecht: Kluwer Acad. Publ., pp. 1–22, ISBN 978-0-792-34668-5, MR 1468786
• Aluffi, Paolo (2009), "6.4 Example: Subgroups of Cyclic Groups", Algebra, Chapter 0, Graduate Studies in Mathematics, vol. 104, American Mathematical Society, pp. 82–84, ISBN 978-0-8218-4781-7
• Bourbaki, Nicolas (1998-08-03) [1970], Algebra I: Chapters 1-3, Elements of Mathematics, vol. 1 (softcover reprint ed.), Springer Science & Business Media, ISBN 978-3-540-64243-5
• Coxeter, H. S. M.; Moser, W. O. J. (1980), Generators and Relations for Discrete Groups, New York: Springer-Verlag, p. 1, ISBN 0-387-09212-9
• Lajoie, Caroline; Mura, Roberta (November 2000), "What's in a name? A learning difficulty in connection with cyclic groups", For the Learning of Mathematics, 20 (3): 29–33, JSTOR 40248334
• Cox, David A. (2012), Galois Theory, Pure and Applied Mathematics (2nd ed.), John Wiley & Sons, Theorem 11.1.7, p. 294, doi:10.1002/9781118218457, ISBN 978-1-118-07205-9
• Gallian, Joseph (2010), Contemporary Abstract Algebra (7th ed.), Cengage Learning, Exercise 43, p. 84, ISBN 978-0-547-16509-7
• Gannon, Terry (2006), Moonshine beyond the monster: the bridge connecting algebra, modular forms and physics, Cambridge monographs on mathematical physics, Cambridge University Press, p. 18, ISBN 978-0-521-83531-2, Z_n is simple iff n is prime.
• Jungnickel, Dieter (1992), "On the uniqueness of the cyclic group of order n", American Mathematical Monthly, 99 (6): 545–547, doi:10.2307/2324062, JSTOR 2324062, MR 1166004
• Fuchs, László (2011), Partially Ordered Algebraic Systems, International series of monographs in pure and applied mathematics, vol. 28, Courier Dover Publications, p. 63, ISBN 978-0-486-48387-0
• Kurzweil, Hans; Stellmacher, Bernd (2004), The Theory of Finite Groups: An Introduction, Universitext, Springer, p. 50, ISBN 978-0-387-40510-0
• Motwani, Rajeev; Raghavan, Prabhakar (1995), Randomized Algorithms, Cambridge University Press, Theorem 14.14, p. 401, ISBN 978-0-521-47465-8
• Ore, Øystein (1938), "Structures and group theory. II", Duke Mathematical Journal, 4 (2): 247–269, doi:10.1215/S0012-7094-38-00419-3, hdl:10338.dmlcz/100155, MR 1546048
• Rotman, Joseph J. (1998), Galois Theory, Universitext, Springer, Theorem 62, p. 65, ISBN 978-0-387-98541-1
• Stallings, John (1970), "Groups of cohomological dimension one", Applications of Categorical Algebra (Proc. Sympos. Pure Math., Vol. XVIII, New York, 1968), Providence, R.I.: Amer. Math. Soc., pp. 124–128, MR 0255689
• Stewart, Ian; Golubitsky, Martin (2010), Fearful Symmetry: Is God a Geometer?, Courier Dover Publications, pp. 47–48, ISBN 978-0-486-47758-9
• Vilfred, V. (2004), "On circulant graphs", in Balakrishnan, R.; Sethuraman, G.; Wilson, Robin J. (eds.), Graph Theory and its Applications (Anna University, Chennai, March 14–16, 2001), Alpha Science, pp. 34–36, ISBN 8173195692
• Vinogradov, I. M. (2003), "§ VI PRIMITIVE ROOTS AND INDICES", Elements of Number Theory, Mineola, NY: Dover Publications, pp. 105–132, ISBN 0-486-49530-2

추가 정보

• Herstein, I. N. (1996), Abstract algebra (3rd ed.), Prentice Hall, pp. 53–60, ISBN 978-0-13-374562-7, MR 1375019

외부 링크

• Milne, 그룹 이론, http://www.jmilne.org/math/CourseNotes/gt.html
• 순환 그룹에 대한 소개
• Weisstein, Eric W. "Cyclic Group". MathWorld.
• GroupNames의 소순서 순환 그룹