신호 흐름 그래프

신호 흐름 그래프 또는 신호 흐름 그래프(SFG)는 Claude Shannon이 발명했지만 종종 용어를 ^[1]만든 Samuel Jefferson Mason의 이름을 따서 Mason 그래프로 불리는 ^[2]특수 흐름 그래프이며 노드가 시스템 변수를 나타내고 분기(테두리, 호 또는 화살표)가 노드 쌍 간의 기능적 연결을 나타냅니다. 따라서 신호 흐름 그래프 이론은 지향 그래프 이론도 포함하는 지향 그래프(디그래프라고도 함)의 이론을 기반으로 합니다. 물론 이 수학적인 디그래프 이론은 그 응용과는 별개로 존재합니다.^[3][4]

SFG는 가장 일반적으로 사이버 물리 시스템을 형성하는 물리적 시스템 및 그 컨트롤러의 신호 흐름을 나타내는 데 사용됩니다. 그들의 다른 용도 중에는 다양한 전자 네트워크 및 증폭기, 디지털 필터, 상태 가변 필터 및 일부 다른 유형의 아날로그 필터에서 신호 흐름을 표현하는 것이 있습니다. 거의 모든 문헌에서 신호 흐름 그래프는 일련의 선형 방정식과 연관되어 있습니다.

역사

Wai-Kai Chen은 "신호 흐름 그래프의 개념은 원래 아날로그 컴퓨터를 다루는 데 있어 Shannon[1942]^[1]에 의해 고안되었습니다. 신호 흐름 그래프의 공식화에 대한 최대 신용은 일반적으로 메이슨[1953],^[2] [1956]으로 확장됩니다.^[5] 그는 신호 흐름 그래프 기법을 사용하여 몇몇 어려운 전자 문제를 비교적 간단한 방법으로 해결하는 방법을 보여주었습니다. 신호 흐름 그래프라는 용어는 전자 문제에 대한 원래의 적용과 연구 중인 시스템의 전자 신호 및 흐름도와의 연관성 때문에 사용되었습니다."^[6]

Lorens는 다음과 같이 썼습니다: "메이슨의 작업 이전에, C.E[1]. Shannon은 현재 플로우 그래프로 알려진 많은 특성을 계산했습니다. 안타깝게도 이 논문은 원래 분류가 제한되어 있었고 자료에 접근할 수 있는 사람은 거의 없었습니다."^[7]

"메이슨 그래프의 그래프 결정인자를 평가하기 위한 규칙은 섀넌[1942]이 수학적 귀납법을 사용하여 처음 제시하고 증명했습니다. 그의 작품은 메이슨이 1953년 그의 고전 작품을 출판한 후에도 본질적으로 알려지지 않은 채로 남아있었습니다. 3년 후, 메이슨[1956]은 규칙을 재발견하고, 결정 요인의 값과 변수가 그래프에 추가됨에 따라 어떻게 변하는지를 고려함으로써 규칙을 증명했습니다. [...]"^[8]

응용영역

Robichaud et al. 는 다음과 같이 SFG의 적용 영역을 식별합니다.^[9]

"이러한 네트워크와 유사한 모든 물리적 시스템(이상적인 변압기, 능동 소자 및 자이레이터로 구성됨)은 [여기]에서 개발된 기술의 적용 영역을 구성합니다. 트렌트는^[10] 다음 조건을 만족하는 모든 물리적 시스템이 이 범주에 속한다는 것을 보여주었습니다.

1. 유한 덩어리 시스템은 여러 가지 단순한 부분으로 구성되어 있으며, 각각은 두 가지 유형의 스칼라 변수와 시스템 매개 변수를 사용한 방정식으로 정의할 수 있는 알려진 동적 특성을 가지고 있습니다. 첫 번째 유형의 변수는 적어도 개념적으로 요소의 두 연결점에 표시 기기를 부착하여 측정할 수 있는 양을 나타냅니다. 두 번째 유형의 변수는 미터를 요소와 직렬로 연결하여 측정할 수 있는 양을 특징으로 합니다. 상대 속도 및 위치, 압력 차이 및 전압은 일반적으로 1등급의 양인 반면 전류, 힘, 열 흐름 속도는 두 번째 유형의 변수입니다. 파이어스톤은 변수 전체와 변수 전체의 이름으로 이 두 가지 유형의 변수를 구별한 최초의 사례입니다.
2. 첫 번째 유형의 변수는 키르히호프의 전압 법칙과 유사한 메시 법칙을 따라야 하고, 두 번째 유형의 변수는 키르히호프의 현재 법칙과 유사한 발생 법칙을 만족해야 합니다.
3. 두 유형 변수의 적절한 곱의 물리적 차원이 일치해야 합니다. 이러한 조건이 만족되는 시스템의 경우 선택된 변수에 의해 설명되는 시스템의 동적 특성과 동형인 선형 그래프를 그릴 수 있습니다. 이 선형 그래프뿐만 아니라 전기 네트워크에도 [...] 기술을 직접 적용하여 시스템의 신호 흐름 그래프를 얻을 수 있습니다."

기본 흐름 그래프 개념

메이슨은 기본 개념을 설명하기 위해 다음 그림과 그 의미를 소개했습니다.^[2]

그림의 단순한 흐름 그래프에서, 노드의 기능 의존성은 들어오는 화살표로 표시되고, 이 영향을 시작하는 노드는 이 화살표의 시작이며, 가장 일반적인 형태에서 신호 흐름 그래프는 수신 노드에서 처리에 영향을 미치는 노드만을 들어오는 화살표로 표시하고, 각 노드에서 i, 들어오는 변수는 해당 노드와 연관된 함수에 따라 처리됩니다. 예를 들어 F_i. (a)의 흐름도는 명시적인 관계 집합을 나타냅니다.

${\displaystyle {\begin{aligned}x_{\mathrm {1}}&={\text{독립 변수}\x_{\mathrm {2}}&=F_{2}(x_{\mathrm {1}},x_{\mathrm {3}})\x_{\mathrm {3}&=F_{3}(x_{\mathrm {1}},x_{\mathrm {2})\\\end{aligned}}}$

노드 x는₁ 화살표가 들어오지 않기 때문에 고립된 노드입니다₂. x와₃ x에 대한 방정식은 그림의 (b)와 (c)에 표시된 그래프를 갖습니다.

이러한 관계는 모든 노드에 대해 수신되는 입력 신호를 처리하는 함수를 정의합니다. 각 비-소스 노드는 어떤 방식으로 입력 신호를 결합하고, 결과 신호를 각 발신 분기를 따라 방송합니다. "흐름 그래프는 원래 Mason에 의해 정의된 것처럼 선형이든 아니든 일련의 함수 관계를 의미합니다."^[9]

그러나 일반적으로 사용되는 메이슨 그래프는 각 노드가 단순히 들어오는 화살표를 합산하고 각 분기가 관련된 시작 노드만 포함한다고 가정할 때 더 제한됩니다. 따라서 이 보다 제한적인 접근 방식에서 노드₁ x는 영향을 받지 않지만 다음과 같습니다.

${\displaystyle x_{2}=f_{21}(x_{1})+f_{23}(x_{3})}$

${\displaystyle x_{3}=f_{31}(x_{1})+f_{32}(x_{2})+f_{33}(x_{3})\ ,}$

그리고 이제 함수 f는_ij 각 노드와 관련된 일반적인 관계가 아니라 노드 x_i, x를_j 연결하는 신호 흐름 분기 ij와 관련될 수 있습니다. 노드가₃ x에 대해₃₃ f와 같이 자기 자신에게 기여하는 것을 자기 루프라고 합니다. 종종 이러한 함수는 단순히 곱셈 계수(종종 투과율 또는 이득이라고 함)입니다. 예를 들어 f(x)=cx이며, 여기서 c는 스칼라이지만 라플라스 변환 변수와 같은 일부 매개 변수의 함수일 수 있습니다. 신호 흐름 그래프는 선형 미분 방정식의 시스템을 나타내기 때문에 라플라스 변환 신호와 함께 매우 자주 사용됩니다. 이 경우 투과율인 c(s)는 종종 전달 함수라고 불립니다.

변수 선택

일반적으로 복잡한 시스템에서 변수를 선택하는 방법은 여러 가지가 있습니다. 각 선택에 해당하는 방정식 체계를 작성하고 각 방정식 체계를 그래프로 나타낼 수 있습니다. 이 방정식의 공식화는 연구 중인 시스템의 개략도에서 직접 그래프를 그릴 수 있는 마음대로 사용할 수 있는 기술이 있으면 직접적이고 자동적으로 됩니다. 이렇게 얻은 그래프의 구조는 간단한 방식으로 도식도의 토폴로지와 관련이 있으며, 그래프를 얻기 위해 암묵적으로라도 방정식을 고려하는 것은 불필요합니다. 경우에 따라 도식도의 흐름 그래프를 상상하기만 하면 흐름 그래프를 그릴 필요도 없이 원하는 답을 얻을 수 있습니다.

— Robichaud^[11]

비일관성

Robichaud et al.은 "신호 흐름 그래프는 그것이 유도된 방정식과 동일한 정보를 포함하지만 그래프와 방정식 시스템 사이에 일대일 대응은 존재하지 않습니다. 한 시스템은 방정식이 왼쪽에 쓰여진 변수를 정의하는 데 사용되는 순서에 따라 다른 그래프를 제공할 것입니다."^[9] 모든 방정식이 모든 종속 변수와 관련되어 있으면 n!개의 SFG를 선택할 수 있습니다.^[12]

선형 신호 흐름 그래프

선형 신호 흐름 그래프(SFG) 방법은 관련 이론에 의해 연구된 바와 같이 선형 시간 불변 시스템에만 적용됩니다. 관심 있는 시스템을 모델링할 때 첫 번째 단계는 원인과 결과를 할당하지 않고 시스템의 작동을 나타내는 방정식을 결정하는 것입니다(이를 원인 모델링이라고 합니다).^[13] 그런 다음 이 방정식 시스템에서 SFG가 유도됩니다.

선형 SFG는 점으로 표시된 노드와 화살표로 표시된 가중 방향 분기로 구성됩니다. 노드는 방정식의 변수이고 분기 가중치는 계수입니다. 신호는 화살표로 표시된 방향의 분기만 통과할 수 있습니다. SFG의 요소는 제한된 방정식을 나타내기에 충분한 계수와 덧셈에 의한 곱셈 연산만을 나타낼 수 있습니다. 신호가 지시된 방향으로 분기를 통과할 때 신호는 분기의 무게를 곱합니다. 두 개 이상의 분기가 동일한 노드로 직접 연결되면 해당 분기의 출력이 추가됩니다.

선형 대수학 또는 미분 방정식으로 설명되는 시스템의 경우 신호 흐름 그래프는 시스템을 설명하는 방정식 시스템과 수학적으로 동일하며 노드를 지배하는 방정식은 해당 노드로 들어오는 분기를 합산하여 각 노드에 대해 발견됩니다. 이러한 수신 분기는 연결된 노드 값에 연결 분기의 가중치를 곱한 값으로 표시되는 다른 노드의 기여도를 전달합니다. 일반적으로 일부 매개 변수(예: Laplace 변환 변수)의 실수 또는 함수입니다.

선형 활성 네트워크의 경우 Choma는 ^[14]"일반적으로 언급되는 '신호 흐름 표현'[또는 '그래프]를 통해 네트워크의 관련 분기 변수 간의 대수적 관계를 표시함으로써 적용된 입력 신호가 입력에서 출력으로 '흐름'되는 방식에 대한 명확한 그림을 그리는 다이어그램을 의미합니다. 항구."

Chen은 SFG 분석의 동기에 대해 다음과 같이 설명합니다.^[15]

"선형 시스템의 분석은 궁극적으로 선형 대수 방정식의 해를 감소시킵니다. 시스템을 해결하는 기존의 대수적 방법에 대한 대안으로 시스템과 연관된 특정 방향 그래프의 속성을 고려하여 해를 얻을 수 있습니다." [하위 섹션 참조: 선형 방정식을 푸는 중입니다.] "방정식의 미지수는 그래프의 노드에 해당하는 반면, 그들 사이의 선형 관계는 노드를 연결하는 방향 에지의 형태로 나타납니다. ...많은 경우 관련 지시 그래프는 → 관련 방정식을 먼저 공식화할 필요 없이 물리적 시스템 검사를 통해 직접 설정할 수 있습니다.."

기본구성품

선형 신호 흐름 그래프는 다음과 같은 형태의 선형 방정식^[16] 시스템과 관련이 있습니다.

${\displaystyle {\begin{aligned}x_{\mathrm {j}}&=\sum _{\mathrm {k} =1}^{\mathrm {N}}t_{\mathrm {jk}}x_{\mathrm {k}}\end{aligned}}$

$여기$서 ${\displaystyle j_{}}$ ${\displaystyle k_{}}$ ${\displaystyle t_{jk}}$ = 투과율(또는 이득)은 $x$ ${\displaystyle k_{}}$ ${\displaystyle x_{k}}$ ~ $x$ ${\displaystyle j_{}}$ ${\displaystyle x_{j}$입니다$.$

오른쪽 그림은 신호 흐름 그래프(SFG)의 다양한 요소와 구성을 보여줍니다.^[17]

표시(a)는 노드입니다. 이 경우 노드에는 $x{\displaystyle }$ ${\displaystyle x}$라는 레이블이 지정됩니다$.$ 노드는 변수 또는 신호를 나타내는 정점입니다.

소스 노드에는 나가는 분기만 있습니다(독립 변수를 나타냅니다). 특수한 경우로서, 입력 노드는 노드로부터 멀어지는 방향을 가리키는 하나 이상의 부착된 화살표들을 갖고, 노드를 가리키는 화살표들은 없는 것을 특징으로 하는 입력 노드. 모든 개방형 완전한 SFG는 적어도 하나의 입력 노드를 가질 것입니다.

출력 또는 싱크 노드에는 들어오는 분기만 있습니다(종속 변수를 나타냄). 모든 노드가 출력이 될 수 있지만 명확성을 제공하기 위해 명시적인 출력 노드가 자주 사용됩니다. 명시적인 출력 노드는 노드를 가리키는 하나 이상의 부착된 화살표를 갖고 노드를 가리키는 화살표는 없는 것을 특징으로 합니다. 명시적인 출력 노드는 필요하지 않습니다.

혼합 노드에는 들어오는 분기와 나가는 분기가 모두 있습니다.

표시(b)는 곱셈 $이득$이 m ${\displaystyle$ m$}$인 분기입니다$.$ 의미는 화살표 끝에 있는 출력이 화살표 끝에 있는 입력의 $m{\displaystyle }$ ${\displaystyle$ m$}$배라는$$ 것입니다. 게인은 단순 상수이거나 함수일 수 있습니다(예: Laplace, Fourier 또는 Z 변환 관계의 $경우$ ${\displaystyle$ s$\},$$$ω {\displaystyle$$\$omega$$$}$$또는 z${\displaystyle$z}와 같은 일부 변환 변수의 함수).

그림 (c)는 곱셈 이득이 1인 가지입니다. 이득이 누락된 경우에는 통일성으로 가정합니다.

${\$의 (d) $V$는 입력 노드입니다$$. 이 경우 ${\$의 $V$에 $이득{\displaystyle }$ ${\displaystyle$ m$}$을 곱합니다$$$.$

표시(e) $I{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{out}}_{}}$ ${\$은 명시적인 출력 노드이며, 들어오는 에지는 $m{\displaystyle }$ ${\displaystyle$ m$}$의 이득을 가집니다$.$

(f)는 덧셈을 묘사합니다. 두 개 이상의 화살표가 노드를 가리킬 때 가장자리가 전달하는 신호가 추가됩니다.

그림 (g)는 단순한 루프를 보여줍니다. 루프 이득은 $A{\displaystyle }$× ${\displaystyle m}$ ${\displaystyle$ A$\times$ m$}$입니다$.$

그림 (h)는 $식$ Z = ${\displaystyle a}$ X${\displaystyle }$+$$by Y {\displaystyle Z = aX+bY}를 나타냅니다.

선형 SFG 이론에서 사용되는 용어는 다음을 포함합니다.^[17]

• 경로. 경로는 분기 화살표로 표시된 방향으로 교차하는 연속적인 분기 집합입니다.
  • 오픈 패스. 노드를 다시 방문하지 않으면 경로가 열립니다.
  • 전진경로. 입력 노드(소스)에서 출력 노드(싱크)로 가는 경로로 노드를 다시 방문하지 않습니다.
• 경로 이득: 경로에 있는 모든 가지의 이득의 곱.
• 루프. 폐쇄 경로. (동일한 노드에서 시작되고 종료되며 노드가 두 번 이상 터치되지 않습니다.)
• 루프 이득: 루프에 있는 모든 가지의 이득의 곱.
• 비터치 루프입니다. 비접촉 루프에는 공통 노드가 없습니다.
• 그래프 축소. 그래프 변환을 사용하여 그래프에서 하나 이상의 노드를 제거합니다.
  • 잔차 노드입니다. 그래프 축소의 모든 고려된 프로세스에서 새 그래프에 유지될 노드를 잔차 노드라고 합니다.^[2]
• 노드를 분할합니다. 노드를 분할하는 것은 노드를 두 개의 절반 노드로 분할하는 것에 해당하며, 하나는 싱크이고 다른 하나는 소스입니다.^[18]
• 인덱스: 그래프의 인덱스는 그래프의 모든 루프를 제거하기 위해 분할해야 하는 최소 노드 수입니다.
  • 인덱스 노드. 그래프의 인덱스를 결정하기 위해 분할된 노드를 인덱스 노드라고 하며 일반적으로 이 노드는 고유하지 않습니다.

소스 및 싱크에 대한 체계적인 감소

신호 흐름 그래프는 그래프 변환 규칙에 의해 단순화될 수 있습니다.^[19][20][21] 이러한 단순화 규칙을 신호 흐름 그래프 대수라고도 합니다.^[22] 이 감소의 목적은 관심 있는 종속 변수(잔여 노드, 싱크)를 독립 변수(소스)와 연관시키는 것입니다.

선형 신호 흐름 그래프의 체계적인 감소는 선형 방정식을 풀기 위한 가우스-조르단 제거 방법과 동등한 그래픽 방법입니다.^[23]

아래에 제시된 규칙은 신호 흐름 그래프가 "최소 잔류 형태"로 감소될 때까지 계속 적용될 수 있습니다. 추가적인 감소는 루프 제거 또는 종속 변수를 나타내는 싱크 노드를 독립 변수를 나타내는 소스 노드에 직접 연결하는 목표와 함께 "감소 공식"의 사용을 필요로 할 수 있습니다. 이러한 방법을 통해 입력 및 출력 및 인덱스 노드만 남을 때까지 내부 노드를 연속적으로 제거하여 모든 신호 흐름 그래프를 단순화할 수 있습니다.^[24][25] Robichaud는 체계적인 흐름 그래프 축소 과정을 다음과 같이 설명했습니다.

그래프의 축소는 특정 노드를 제거하여 관심 변수만을 보여주는 잔차 그래프를 얻는 방법으로 진행됩니다. 이러한 노드 제거를 "노드 흡수"라고 합니다. 이 방법은 방정식 체계에서 원하지 않는 변수를 연속적으로 제거하는 익숙한 과정에 가깝습니다. 그래프에서 해당 노드를 제거하여 변수를 제거할 수 있습니다. 그래프를 충분히 줄이면 모든 변수에 대한 해를 얻을 수 있으며 이는 그래프의 다양한 축소 방법에 대한 설명에서 염두에 두어야 할 목표입니다. 그러나 실제로는 축소 기법을 사용하여 그래프를 몇 가지 기본 관계를 표현하는 잔차 그래프로 변환합니다. 메이슨의 법칙을 적용하면 완전한 해결책을 더 쉽게 얻을 수 있습니다.^[26] 그래프 자체가 축소 과정을 프로그래밍합니다. 실제로 그래프를 간단히 검사하면 기본 변환, 루프 제거 또는 환원 공식을 사용하여 수행되는 다양한 단계의 환원을 쉽게 제안할 수 있습니다.^[26]

— Robichaud, Signal flow graphs and applications, 1962

Robichaud는 알고리즘을 사용하여 흐름 그래프를 디지털 방식으로 줄이기 위해 단순한 흐름 그래프의 개념을 일반화된 흐름 그래프로 확장합니다.

축소 과정을 설명하기 전에...그래프와 선형방정식의 대응관계를 일반화해야 합니다.일반화된 그래프는 변수 그룹 간의 일부 작동 관계를 나타냅니다.일반화된 그래프의 각 분기에는 해당 분기의 말단에 있는 노드로 표현되는 변수 간의 관계를 제공하는 행렬이 연결됩니다.^[27] 기본 변환 [그림 7.2, 페이지 184에서 Robichaud에 의해 정의됨]과 루프 축소는 축소 공식에 의해 그래프의 노드 j를 제거할 수 있습니다. [Robichaud의 식 7-1에서 설명됨]. 축소 공식을 사용하면 어떤 순서의 그래프도 항상 축소할 수 있습니다. [축소 후] 최종 그래프는 싱크 노드의 변수가 소스의 함수로 명시적으로 표현되는 캐스케이드 그래프가 될 것입니다. 메이슨의 법칙은 분명히 적용할 수 없기 때문에 이것은 일반화된 그래프를 줄이는 유일한 방법입니다.^[28]

— Robichaud, Signal flow graphs and applications, 1962

기본 변환의 정의는 저자마다 다릅니다.

• 일부 저자는 병렬 에지 이득의 합과 직렬 에지 이득의 곱을 기본 변환으로 간주할 뿐 자기^[23][29] 루프의 제거는 고려하지 않습니다.
• 다른 저자들은 자기 루프의 제거를 기본적인 변환으로^[30] 간주합니다.

평행 모서리. 평행한 에지를 원래 이득의 합과 같은 이득을 갖는 단일 에지로 대체합니다.

왼쪽 그래프는 노드 사이에 평행한 모서리를 가지고 있습니다. 오른쪽에서 이 평행한 에지는 각 원래 에지의 이득의 합과 동일한 이득을 갖는 단일 에지로 대체되었습니다.

N과 노드 I₁ 사이의 감소에 해당하는 방정식은 다음과 같습니다.

${\displaystyle {\begin{aligned}N&=I_{\mathrm {1} }f_{\mathrm {1} }+I_{\mathrm {1} }f_{\mathrm {2} }+I_{\mathrm {1} }f_{\mathrm {3} }+...\\N&=I_{\mathrm {1} }(f_{\mathrm {1} }+f_{\mathrm {2} }+f_{\mathrm {3} })+...\\\end{align}}}$

가장자리를 내보내고 있습니다. 노드의 소스에서 직접 흐르는 에지로 유출 에지를 대체합니다.

왼쪽 그래프에는 유입되는 노드와 유출되는 노드 사이에 중간 노드 N이 있습니다. 오른쪽 그래프는 N을 통해 전송하지 않고 이 노드 집합 간의 직접 흐름을 보여줍니다.

단순화를 위해 N과 그 유입량은 표시되지 않습니다. N에서 유출되는 것이 제거됩니다.

N의 입력 신호와 출력 신호를 직접적으로 연관시키는 감소에 해당하는 방정식은 다음과 같습니다.

${\displaystyle {\begin{aligned}N&=I_{\mathrm {1} }f_{\mathrm {1} }+I_{\mathrm {2} }f_{\mathrm {2} }+I_{\mathrm {3} }f_{\mathrm {3} }\\O_{\mathrm {1} }&=g_{\mathrm {1} }N\\O_{\mathrm {2} }&=g_{\mathrm {2} }N\\O_{\mathrm {3} }&=g_{\mathrm {3} }N\\O_{\mathrm {1} }&=g_{\mathrm {1} }(I_{\mathrm {1} }f_{\mathrm {1} }+I_{\mathrm {2} }f_{\mathrm {2} }+I_{\mathrm {3} }f_{\mathrm {3} })\\O_{\mathrm {2} }&=g_{\mathrm {2} }(I_{\mathrm {1} }f_{\mathrm {1} }+I_{\mathrm {2} }f_{\mathrm {2} }+I_{\mathrm {3} }f_{\mathrm {3} })\\O_{\mathrm {3} }&=g_{\mathrm {3} }(I_{\mathrm {1} }f_{\mathrm {1} }+I_{\mathrm {2} }f_{\mathrm {2} }+I_{\mathrm {3} }f_{\mathrm {3} })\\O_{\mathrm {1} }&=I_{\mathrm {1} }f_{\mathrm {1} }g_{\mathrm {1} }+I_{\mathrm {2} }f_{\mathrm {2} }g_{\mathrm {1} }+I_{\mathrm {3} }f_{\mathrm {3} }g_{\mathrm {1} }\\O_{\mathrm {2} }&=I_{\mathrm {1} }f_{\mathrm {1} }g_{\mathrm {2} }+I_{\mathrm {2} }f_{\mathrm {2} }g_{\mathrm {2} }+I_{\mathrm {3} }f_{\mathrm {3} }g_{\mathrm {2} }\\O_{\mathrm {3} }&=I_{\mathrm {1} }f_{\mathrm {1} }g_{\mathrm {3} }+I_{\mathrm {2} }f_{\mathrm {2} }g_{\mathrm {3} }+I_{\mathrm {3} }f_{\mathrm {3} }g_{\mathrm {3} }\\\end{aligned}}}$

제로 신호 노드.

값이 0인 것으로 결정된 노드에서 유출 모서리를 제거합니다.

노드의 값이 0이면 노드의 유출 에지를 제거할 수 있습니다.

유출이 없는 노드.

유출 없이 노드를 제거합니다.

이 경우 N은 관심 변수가 아니며 나가는 간선이 없으므로 N과 유입 간선을 제거할 수 있습니다.

셀프 루핑 에지. 들어오는 에지의 이득을 조정하여 루프 에지를 대체합니다.

왼쪽의 그래프는 노드 N에서 g의 이득을 가지는 루핑 에지를 가지고 있습니다. 오른쪽은 루핑 에지가 제거되었으며 모든 유입 에지는 이득을 (1-g)으로 나눕니다.

N과 N의 모든 입력 신호 사이의 감소에 해당하는 방정식은 다음과 같습니다.

구현

인과 방정식 시스템에서 SFG를 구축하고 SFG의 이득을 해결하기 위한 위의 절차는 분석에서 발생하는 기계적 상징 프로세스에 대한 기계적 도움을 제공하는 온라인 시스템인 ^[32]MATHLAB 68의 추가 기능으로 구현되었습니다^[31].

선형방정식 풀기

신호 흐름 그래프를 사용하여 동시 선형 방정식 집합을 풀 수 있습니다.^[33] 방정식 집합은 일관적이어야 하며 모든 방정식은 선형 독립적이어야 합니다.

방정식을 "표준 형태"에 넣는 것

각각의_j y가 알려진 값이고 각각의_j x가 알려지지 않은 값인 N개의 미지수를 갖는 M개의 방정식에 대하여, 다음과 같은 형태의 알려진 각각의 방정식이 있습니다.

= N c$j$k x k = y j {\displae {\begin{aligned}\sum_{\mahrm {k} =1}^{\mathrm {N} }c_{\mathrm {jk} }x_{\mathm {k} }&=y_{\mathrm {j} }\end{aligned}}; 1 ≤ j ≤ M인 동시 선형 방정식의 일반적인 형태

특히 단순한 경우에는 이러한 형태의 방정식을 사용하여 신호 흐름 그래프를 설정하는 것이 가능하지만, 현재 제시된 것과 같이 어떤 방정식 세트에 대해서도 쉽게 작동하는 일반적인 절차가 가능합니다. 진행하려면 먼저 방정식을 다음과 같이 다시 씁니다.

${\displaystyle {\begin{aligned}\sum_{\mathrm {k} =1}^{\mathrm {N}}c_{\mathrm {jk}}x_{\mathrm {k}}-y_{\mathrm {j}}&=0\end{aligned}}$

로 다시 쓰입니다.

${\displaystyle {\begin{aligned}\sum_{\mathrm {k=1}}^{\mathrm {N}}c_{\mathrm {jk}}x_{\mathrm {k}}+x_{\mathrm {j}-y_{\mathrm {j}}&=x_{\mathrm {j}}\end{aligned}}$

그리고 마침내 다시 쓰이게 되었습니다.

= 1c jk + δ j k ) xk - y j = x {\displaystyle {\mathrm {aligned}\sum _{\athrm {k=1} }^{\mathrm {N}(c_{\mathrm }+\delta _{\mathrm {jk} })x_{\mathrm {k} }-y_{\mathm {j} }&=x_{\mathrm {j} }\end{aligned}}; 신호 흐름 그래프로 표현하기에 적합한 형식입니다.

여기서 δ = 크로네커 델타

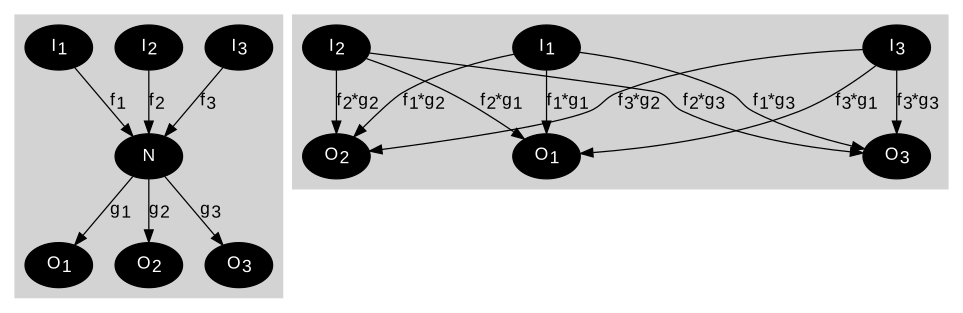
이제 신호 흐름 그래프는 이러한 방정식 중 하나를 선택하고 오른쪽에 있는 노드를 지정하여 배열됩니다. 이것은 노드가 '+1'을 포함한 무게의 분기로 자신에게 연결되어 흐름 그래프에서 셀프 루프를 만드는 노드입니다. 이 수식의 다른 항들은 이 노드를 먼저 이 수식의 소스에 연결한 다음 이 노드에 연결된 모든 다른 분기에 연결합니다. 모든 방정식은 이러한 방식으로 처리된 다음, 각 사건 분기는 각각의 방출 노드에 연결됩니다. 예를 들어, 세 변수의 경우는 그림에 나와 있으며 첫 번째 방정식은 다음과 같습니다.

${\displaystyle x_{1}=\left(c_{11}+1\right)x_{1}+c_{12}x_{2}+c_{13}x_{3}-y_{1}\ ,}$

여기서 이 방정식의 우변은 노드 x에₁ 결합된 가중 화살표의 합입니다.

모든 노드의 처리에 기본적인 대칭이 있기 때문에 단순한 시작점은 각 노드를 정규 다각형의 한 꼭짓점에 배치하는 것입니다. 일반 계수 {c_in}를 사용하여 표현하면 각 노드의 환경은 인덱스의 순열을 제외한 나머지와 동일합니다. 세 개의 동시 방정식 집합에 대한 이러한 구현은 그림에 나와 있습니다.^[34]

흔히 알려진 값인_j y를 주요 원인으로, 미지수 값인_j x를 효과로 간주하지만, 이러한 해석과 상관없이 방정식 집합의 마지막 형식은 신호 흐름 그래프로 나타낼 수 있습니다. 이 점은 '인과성' 해석의 하위 섹션에서 더 자세히 설명합니다.

Mason's gain formula 적용

가장_k 일반적인 경우, 모든 x_j 변수의 값은_k 각 y에서 각 x로의 경로에 대한 메이슨의 이득 공식을 계산하고 중첩을 사용하여 계산할 수 있습니다.

${\displaystyle {\begin{aligned}x_{\mathrm {k}}&=\sum _{\mathrm {j} =1}^{\mathrm {M}}(G_{\mathrm {kj})y_{\mathrm {j}}\end{aligned}}$

여기서 G = 입력 y부터 변수 x까지의 모든 경로에 대해 계산된 메이슨 이득 공식의 합.

일반적으로, y에서_jk 변수 x까지의 경로는 N-1이므로 G를_kj 계산하기 위한 계산 노력은 N-1에 비례합니다. y의_j 값은 M이므로, G는_kj x의_k 단일 값에 대해 M번 계산되어야 합니다. 단일 x_k 변수를 계산하는 계산 노력은 (N-1)(M)에 비례합니다. 모든_k x개의 변수를 계산하는 노력은 (N)(N-1)(M)에 비례합니다. 만약 N개의 방정식과 N개의 미지수가 있다면, 계산 노력은³ N의 순서입니다.

블록 다이어그램 관련

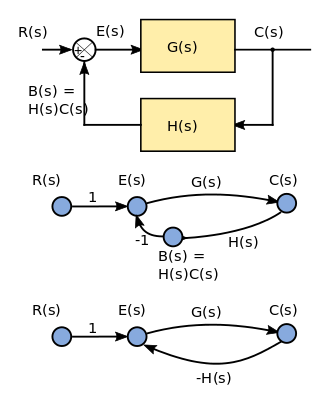
일부 저자의 경우, 선형 신호 흐름 그래프는 SFG가 지향 그래프로 표현되는 선형 대수 방정식을 엄격하게 설명한다는 ^[35]점에서 블록 다이어그램보다 더 제한적입니다.

다른 저자의 경우 선형 블록 다이어그램과 선형 신호 흐름 그래프는 시스템을 묘사하는 동등한 방법이며, 이 중 하나를 사용하여 이득을 해결할 수 있습니다.^[36]

블록 다이어그램과 신호 흐름 그래프 간의 비교 표는 Bakshi & Bakshi에 ^[37]의해 제공되며 다른 표는 Kumar에 의해 제공됩니다.^[38] Barker et al. 에 따르면:^[39]

"신호 흐름 그래프는 동적 시스템을 표현하는 데 가장 편리한 방법입니다. 그래프의 토폴로지가 작고 블록 다이어그램에 적용되는 해당 규칙보다 조작하기 쉬운 규칙을 프로그래밍할 수 있습니다."

그림에는 피드백 시스템에 대한 간단한 블록 다이어그램이 표시되어 있으며 신호 흐름 그래프로 두 가지 해석이 가능합니다. 입력 R(들)은 Laplace 변환된 입력 신호이며, 신호 흐름 그래프에서 소스 노드로 표시됩니다(소스 노드에는 입력 에지가 없습니다). 출력 신호 C는 Laplace 변환 출력 변수입니다. 플로우 다이어그램에서 싱크 노드(싱크에는 출력 에지가 없음)로 표시됩니다. G(s)와 H(s)는 전송 함수이며, H(s)는 출력의 수정된 버전을 입력 B(s)로 피드백하는 역할을 합니다. 두 흐름 그래프 표현은 동등합니다.

'인과성' 해석

메이슨은 "원인과 결과"라는 용어를 SFG에 적용했습니다.^[2]

"그래프를 구성하는 과정은 물리적 시스템을 통해 원인과 결과의 연속을 추적하는 과정 중 하나입니다. 한 변수는 특정 원인에 의한 명시적 효과로 표현되며, 다른 원인에 의한 효과로 인식됩니다."

— S.J. 메이슨: 섹션 IV: 플로우 그래프 기법의 예시적인 적용

이후 많은 저자들에 의해 반복되었습니다.^[40]

"신호 흐름 그래프는 시스템의 구성 요소 간의 인과 관계를 나타내는 또 다른 시각적 도구입니다. S.J. Mason이 선형 시스템의 인과 관계 표현으로 도입한 블록 다이어그램의 단순화된 버전입니다."

— 아서 G.O. 무탐바라: 제어 시스템의 설계 및 분석, 페이지 238

그러나 메이슨의 논문은 일련의 방정식이 "원인과 결과"의 직관적인 개념과 무관한 강조점인 SFG와 어떻게 연결되는지를 매우 자세히 보여주는 것에 관심이 있습니다. 직관은 SFG에 도착하거나 SFG에서 통찰력을 얻는 데 도움이 될 수 있지만 SFG에는 필수적이지 않습니다. SFG의 본질적인 연결은 다음과 같이 Ogata에 의해 설명된 자체 방정식 집합에 있습니다.^[41]

"신호 흐름 그래프는 동시 대수 방정식의 집합을 나타내는 다이어그램입니다. 신호 흐름 그래프 방법을 제어 시스템의 분석에 적용할 때는 먼저 [라플라스 변환 변수] s에서 선형 미분 방정식을 대수 방정식으로 변환해야 합니다."

— 오가타 카츠히코: 현대 제어 공학, 104쪽

여기서 "원인과 결과"에 대한 언급은 없습니다. 그리고 바루츠키에 의해 다음과 같이 말했습니다.^[42]

"블록 다이어그램처럼 신호 흐름 그래프는 시스템의 물리적 구조가 아니라 계산적인 것을 나타냅니다."

— Wolfgang Borutzky, Bond Graph 방법론, 10쪽

"원인과 결과"라는 용어는 SFG에 적용되는 것으로 잘못 해석될 수 있으며, 계산에 기초한 의미가 ^[43]아니라 인과관계에 대한 시스템 관점을 제안하는 것으로 잘못 해석될 수 있습니다. 논의를 명확히 하기 위해 채권 그래프에 대해 제안된 바와 같이 "계산적 인과관계"라는 용어를 사용하는 것이 좋습니다.^[44]

"본드그래프 문헌은 직관적인 인과성의 의미로 해석되는 것을 피하기 위해 시뮬레이션에서 계산의 순서를 나타내는 계산적 인과성이라는 용어를 사용합니다."

"계산적 인과관계"라는 용어는 저항기의 전류와 전압의 예를 사용하여 설명됩니다.^[45]

"따라서 물리적 법칙들의 계산적 인과성은 미리 결정될 수 있는 것이 아니라, 그 법칙의 특별한 사용에 달려 있습니다. 전압 강하를 일으키는 것이 저항기를 통해 흐르는 전류인지, 저항기의 양 끝에서 전위의 차이가 전류를 흐르게 하는 것인지 결론을 내릴 수 없습니다. 물리적으로 이것들은 단순히 하나의 동일한 물리적 현상의 두 가지 동시적 측면입니다. 계산적으로, 우리는 어떤 때는 한 위치를 가정하고 어떤 때는 다른 위치를 가정해야 할 수도 있습니다."

— François Cellier & Ernesto Kofman: §1.5 시뮬레이션 소프트웨어 오늘과 내일, 15페이지

컴퓨터 프로그램이나 알고리즘은 다양한 전략을 사용하여 일련의 방정식을 해결할 수 있습니다. 그들은 다른 변수의 관점에서 일부 변수를 찾는 데 우선 순위를 두는 방법에 있어서 차이가 있습니다. 단순히 솔루션 전략에 관한 이러한 알고리즘 결정은 솔루션의 초기에 종속 변수로 표현된 변수를 "효과"로 설정하고, 현재 "원인"인 나머지 변수에 의해 결정됩니다. 계산적 인과관계라는 의미에서

이 용어를 사용하면 SFG와 관련된 것은 시스템 인과성이 아니라 계산 인과성입니다. 계산적 인과관계와 시스템 인과관계 사이의 연관성에 대해 SFG와 특별히 관련되지 않은 광범위한 철학적 논쟁이 있습니다.^[46]

분석 및 설계를 위한 신호 흐름 그래프

신호 흐름 그래프는 분석, 즉 기존 시스템의 모델을 이해하기 위한 것 또는 합성, 즉 설계 대안의 특성을 결정하기 위한 것에 사용될 수 있습니다.

동적 시스템 분석을 위한 신호 흐름 그래프

동적 시스템의 모델을 구축할 때 Dorf & Bishop은 다음 단계 목록을 제공합니다.^[47]

• 시스템과 시스템의 구성 요소를 정의합니다.
• 수학적 모델을 공식화하고 필요한 가정을 나열합니다.
• 모형을 설명하는 미분방정식을 작성합니다.
• 원하는 출력 변수에 대한 방정식을 풀 수 있습니다.
• 해결책과 가정을 조사합니다.
• 필요한 경우 시스템을 재분석하거나 재설계합니다.

-RC Dorf and RH Bishop, 현대 제어 시스템, 2장, 페이지 2

이 워크플로우에서는 물리적 시스템의 수학적 모델의 방정식을 사용하여 신호 흐름 그래프 방정식을 도출합니다.

설계 합성을 위한 신호 흐름 그래프

신호 흐름 그래프는 설계 공간 탐색(DSE)에서 물리적 구현을 위한 중간 표현으로 사용되었습니다. DSE 프로세스는 다양한 대안 중에서 적합한 솔루션을 모색합니다. 관심 있는 시스템을 구성 요소의 물리 방정식으로 먼저 모델링하는 일반적인 분석 워크플로우와 대조적으로, 설계를 합성하기 위한 사양은 원하는 전송 함수가 될 수 있습니다. 예를 들어, 다른 전략을 사용하면 다른 신호 흐름 그래프가 생성되며, 이 그래프에서 구현이 도출됩니다.^[48] 또 다른 예는 주석이 달린 SFG를 아키텍처 생성기에^[49] 대한 입력으로 연속 시간 동작의 표현으로 사용합니다.

섀넌과 섀넌-합 공식

섀넌의 공식은 아날로그 컴퓨터에서 상호 연결된 증폭기 집합의 이득을 계산하기 위한 분석식입니다. 제2차 세계 대전 중, 클로드 섀넌은 아날로그 컴퓨터의 기능적 작동을 조사하는 동안 자신의 공식을 개발했습니다. 전시 제한 때문에 섀넌의 작품은 그 당시 출판되지 않았고, 1952년 메이슨은 같은 공식을 재발견했습니다.

윌리엄 W. Happ은 위상적으로 닫힌 시스템에 대한 Shannon 공식을 일반화했습니다.^[50] Shannon-Happ 공식은 전달 함수, 민감도 및 오차 함수를 도출하는 데 사용할 수 있습니다.^[51]

일관된 선형 일변 관계 집합의 경우 Shannon-Happ 공식은 직접 치환(비반복)을 사용하여 해를 표현합니다.^[51][52]

나사의 전기 회로 소프트웨어 NASAP는 섀넌-합 공식을 기반으로 합니다.^[51][52]

선형 신호 흐름 그래프 예제

단순 전압 증폭기

이득 a를₁₂ 갖는 증폭기에 의한 신호 V의₁ 증폭은 수학적으로 다음과 같이 기술됩니다.

${\displaystyle V_{2}=a_{12}V_{1}\,}$

그림 1의 신호 흐름 그래프로 표시되는 이 관계는 V가₂ V에₁ 의존하지만 V가₁₂ V에 의존하지 않는다는 것을 의미합니다. Kou 57페이지 참조.^[53]

이상적인 부궤환 증폭기

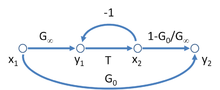
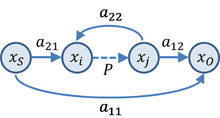
음의 피드백 증폭기에 대한 점근 이득 모델에 대한 가능한 SFG는 그림 3과 같으며, 이 증폭기의 이득에 대한 방정식으로 이어집니다.

${\displaystyle G={\frac {y_{2}}{x_{1}}}$ ${\displaystyle =G_{\infty}\left ({\frac {T}{T+1}}\right)+G_{0}\left({\frac {1}{T+1}}\right)\ .}$

파라미터의 해석은 다음과 같습니다. T = 리턴 비율, G = 직접 증폭기 이득, G = 피드포워드(피드포워드 보상의 경우와 같이 의도적일 수 있음을 indic). 그림 3은 추가 피드백 관계 x = Ty를 추가하여 2포트 네트워크의 경우 그림 2와 유사하다는 흥미로운 측면을 가지고 있습니다.

이 이득식으로부터 매개변수 G와₀ G에_∞ 대한 해석은 명백합니다. 즉, 다음과 같습니다.

${\displaystyle G_{\infty}=\lim_{T\to \infty}G\;\G_{0}=\lim_{T\to 0}G\.}$

특정 이득 관계와 관련된 많은 가능한 SFG가 있습니다. 그림 4는 회로 측면에서 더 쉽게 해석할 수 있는 점근 이득 모델에 대한 또 다른 SFG를 보여줍니다. 이 그래프에서 매개 변수 β는 피드백 계수로, A는 "제어 매개 변수"로 해석되며, 이는 회로의 종속 소스와 관련이 있을 수 있습니다. 이 그래프를 사용하면 이득은

${\displaystyle G={\frac {y_{2}}{x_{1}}}$ ${\displaystyle =G_{0}+{\frac {A}{1-\beta A}}\ .}$

점근 이득 모델에 연결하려면 파라미터 A와 β는 임의의 회로 파라미터가 될 수 없지만 다음과 같이 반환 비율 T에 관련되어야 합니다.

${\displaystyle T=-\beta A\,}$

점근적인 이득은 다음과 같습니다.

${\displaystyle G_{\infty}=\lim_{T\to \infty}G=G_{0}-{\frac {1}{\beta }\.}$

이 결과들을 게인식에 대입하면,

${\displaystyle G=G_{0}+{\frac {1}{\beta }{\frac {-T}{1+T}}$

${\displaystyle =G_{0}+(G_{0}-G_{\infty }){\frac {-T}{1+T}}}$

${\displaystyle =G_{\infty }{\frac {T}{1+T}}+G_{0}{\frac {1}{1+T}\,}$

점근 이득 모델의 공식입니다.

2포트 네트워크를 포함하는 전기 회로

오른쪽 그림은 y-파라미터 2-포트 네트워크를 포함하는 회로를 보여줍니다. V는_in 회로의 입력이고 V는₂ 출력입니다. 두 포트 방정식은 포트 전압과 전류 사이에 일련의 선형 제약을 부과합니다. 말단 방정식은 다른 제약 조건을 부과합니다. 이 모든 제약 조건은 회로 아래의 SFG(Signal Flow Graph)에 표시됩니다. 입력에서 출력까지의 경로는 하나뿐이며 다른 색상으로 표시되며 -Ry의_L21 (전압) 이득을 갖습니다. -Ry_in11, -Ry_L22, Ry_in21L12, RyRy의 세 가지 루프도 있습니다. 때때로 루프는 의도적인 피드백을 나타내지만 두 변수의 관계에 대한 제약을 나타낼 수도 있습니다. 예를 들어 저항기를 설명하는 방정식은 저항기를 통과하는 전류에 대한 저항기를 가로지르는 전압의 비율을 저항이라고 하는 상수라고 말합니다. 이는 전압이 입력이고 전류가 출력이거나 전류가 입력이고 전압이 출력이거나 단순히 전압과 전류가 선형 관계를 갖는 것으로 해석할 수 있습니다. 사실상 회로의 모든 수동 2개의 단자 장치가 SFG에 루프로 표시됩니다.

SFG와 도식은 동일한 회로를 묘사하지만 도식은 또한 회로의 목적을 암시합니다. 도식에 비해 SFG는 어색하지만 Mason의 규칙을 사용하여 검사함으로써 출력 이득에 대한 입력을 적을 수 있다는 장점이 있습니다.

메카트로닉스 : 멀티 루프 피드백이 있는 위치 서보

이 예는 서보 제어 시스템을 나타내기 위해 사용되는 SFG(signal-flow graph)의 대표적인 예이며, SFG의 여러 특징을 보여줍니다. 일부 루프(루프 3, 루프 4 및 루프 5)는 외부에서 의도적으로 설계된 피드백 루프입니다. 점선으로 표시됩니다. 의도적인 피드백 루프가 아닌 고유 루프(루프 0, 루프 1, 루프 2)도 존재하지만, 이들은 마치 그런 것처럼 분석할 수 있습니다. 이 루프는 실선으로 표시됩니다. 3번 루프와 4번 루프는 더 큰 루프 안에 있기 때문에 마이너 루프라고도 합니다.

• 전진 경로는 원하는 위치 명령인 θ로 시작됩니다. 이에 K를_P 곱하면 상수 또는 주파수의 함수가 될 수 있습니다. K는_P DAC의 변환 이득과 DAC 출력에 대한 모든 필터링을 통합합니다. K의_P 출력은 상수 또는 주파수의_ωC 함수가 될 수 있는 K를_V 곱한 속도 명령 V입니다. K의_V 출력은 전류 명령어로_IC V에 상수 또는 주파수의 함수가 될 수 있는 K를_C 곱한 값입니다. K의_C 출력은 증폭기 출력 전압 V입니다_A. 모터 권선은_M 인덕턴스에 인가되는 전압의 적분이지만 전류 I. 모터는 I에_M 비례하는 토크 T를 생성합니다. 영구 자석 모터는 선형 전류 대 토크 기능을 갖는 경향이 있습니다. 전류에서 토크로의 변환 상수는 K입니다_M. 토크 T를 관성 모멘트 M으로 나눈 값이 가속도 α이며, 이를 적분하여 부하 위치 θ를 산출하는 부하 속도 ω를 산출합니다.
• 루프 0의 전진 경로는 가속도는 토크에 비례하고 속도는 가속도의 시간적분이라고 주장합니다. 후진 경로는 속도가 증가함에 따라 토크에 대항하는 마찰 또는 항력이 발생한다고 말합니다. 모든 토크가 마찰을 극복하는 데 사용되고 가속도가 0으로 떨어지는 시점에 도달할 때까지 부하의 토크는 부하 속도에 비례하여 감소합니다. 루프 0은 고유합니다.
• 루프 1은 인덕터 전류와 내부 및 외부 직렬 저항의 상호작용을 나타냅니다. 인덕턴스를 통과하는 전류는 인덕턴스를 가로지르는 전압의 시간 적분입니다. 전압이 처음 인가되면 모든 전압이 인덕터에 나타납니다. 이것은 ${\displaystyle \frac{1초}{}}$ ${\displaystyle \frac{{\mathrm{}}_{}}{}}$ $displaystyle {\frac {1}{s\mathrm {L}$ _${\mathrm {M}}}\,}$을 통과하는 순방향 경로로 표시됩니다$.$ 전류가 증가함에 따라 인덕터 내부 저항 R과_M 외부 저항 R에_S 걸쳐 전압이 떨어집니다. 그러면 인덕터 전체의 전압이 감소하고 피드백 경로 -(R_M + R_S)로 표시됩니다. 전류는 계속 증가하지만, 전류가 모든 전압이 강하되는_M 지점_S(R + R)에 도달할 때까지 지속적으로 감소합니다. 루프 1은 고유합니다.
• 루프2는 모터 백 EMF의 효과를 표현합니다. 영구 자석 모터는 회전할 때마다 발전기와 같은 역할을 하며 권선에 전압을 생성합니다. 회전이 구동축에 가해지는 토크에 의해 발생하는지, 권선에 가해지는 전류에 의해 발생하는지는 중요하지 않습니다. 이 전압을 백 EMF라고 합니다. 역 EMF에 대한 회전 속도의 변환 이득은 G입니다_M. 후면 EMF의 극성은 권선 인덕턴스에 걸쳐 전압을 감소시킵니다. 루프 2는 본질적입니다.
• 루프 3은 외인적입니다. 모터 권선의 전류는 감지 저항을 통과합니다. 감지 저항기를 가로질러 전개된 전압 V는_IM 전력 증폭기 K의_C 음극 단자로 피드백됩니다. 이 피드백은 전압 증폭기가 전압 제어 전류원처럼 작동하게 합니다. 모터 토크는 모터 전류에 비례하기 때문에 출력 토크에 대한 서브 시스템 V는_IC 전압 제어 토크 소스와 같은 역할을 합니다. 이 서브 시스템은 "전류 루프" 또는 "토크 루프"라고 할 수 있습니다. 루프 3은 루프 1과 루프 2의 효과를 효과적으로 감소시킵니다.
• 루프 4는 외인적입니다. 타코미터(실제로 저전력 dc 발전기)는 각속도에 비례하는 출력 전압 V를_ωM 생성합니다. 이 전압은 K의_V 음의 입력으로 공급됩니다. 이_ωC 피드백은 V에서 부하 각속도까지의 하위 시스템이 속도 소스에 대한 전압과 같은 역할을 하게 합니다. 이 서브 시스템을 "속도 루프"라고 부를 수 있습니다. 루프 4는 루프 0과 루프 3의 효과를 효과적으로 감소시킵니다.
• 루프 5는 외인적입니다. 전체적인 위치 피드백 루프입니다. 피드백은 디지털 출력을 생성하는 각도 인코더에서 제공됩니다. 출력_P 위치는 K를 구동하는 DAC를 구동하는 디지털 하드웨어에 의해 원하는 위치에서 차감됩니다. SFG에서 DAC의 변환 이득은 K에_P 포함됩니다.

이 예제에 대한 메이슨 게인 공식 개발은 메이슨의 규칙을 참조하십시오.

신호 흐름 그래프의 용어 및 분류

신호 흐름 그래프가 무엇인지에 대한 문헌상 혼란이 있습니다. 채권 그래프의 발명가인 헨리 페이너는 다음과 같이 쓰고 있습니다. "하지만 신호 흐름 그래프의 감소의 대부분은 부분적으로 가지가 선형이어야 하고 노드가 합산되어야 한다는 잘못된 생각 때문입니다. 그 어떤 가정도 메이슨, 그 자신이 받아들이지 않았습니다!"^[55]

신호 흐름 그래프를 다루는 표준

• IEEE 규격 155-1960, IEEE 회로 표준: 선형 신호 흐름 그래프에 대한 용어 정의, 1960.

이 IEEE 표준은 신호 흐름 그래프를 종속 신호와 독립 신호를 노드로 표현하는 지시된 분기 네트워크로 정의합니다. 들어오는 분기는 분기 신호를 종속 노드에 전달합니다. 종속 노드 신호는 해당 노드에서 들어오는 분기 신호의 대수적 합으로, 즉 노드가 합산됩니다.

상태 전이 신호 흐름 그래프

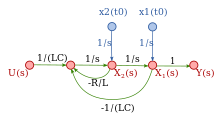
상태 전이 SFG 또는 상태 다이어그램은 상태의 초기 조건을 포함하는 방정식 시스템에 대한 시뮬레이션 다이어그램입니다.^[56]

폐쇄흐름도

폐쇄형 플로우그래프는 폐쇄형 시스템을 설명하며 회로 분석의 위상학적 기법에 대한 엄격한 이론적 기초를 제공하는 데 활용되었습니다.^[50]

• 폐쇄형 플로우그래프 이론의 용어는 다음과 같습니다.
  • 기여 노드. 두 개 이상의 수신 신호에 대한 합산 지점으로 하나의 발신 신호만 발생합니다.
  • 분산 노드. 하나의 수신 신호에서만 발생하는 두 개 이상의 발신 신호에 대한 샘플링 지점입니다.
  • 복합 노드. 기여 노드 및 분배 노드의 수축.
  • 엄격하게 종속적이며 엄격하게 독립적인 노드입니다. 엄밀하게 독립적인 노드는 독립적인 소스를 나타내고, 엄밀하게 종속적인 노드는 미터를 나타냅니다.
  • 열림/닫힘 흐름 그래프. 열린 흐름 그래프에는 엄격하게 종속적이거나 엄격하게 독립적인 노드가 포함되며, 그렇지 않은 경우 닫힌 흐름 그래프입니다.

비선형 흐름 그래프

Mason은 비선형 및 선형 흐름 그래프를 모두 도입했습니다. 이 점을 명확히 하기 위해 메이슨은 다음과 같이 썼습니다: "선형 흐름 그래프는 관련 방정식이 선형인 그래프입니다."^[2]

비선형 분기 함수의 예제

우리는 노드 j의 신호를_j x로 표시합니다. 다음은 선형 시불변 시스템과 관련이 없는 노드 함수의 예입니다.

${\displaystyle {\begin{aligned}x_{\mathrm {j} }&=x_{\mathrm {k} }\times x_{\mathrm {l} }\\x_{\mathrm {k} }&=abs(x_{\mathrm {j} })\x_{\mathrm {l} }&\x_{\mathrm {m} }&=t\times x_{\mathrm {j} }{\text{, 여기서 {text{는 시간을 나타냅니다}\\end{aligned}}$

비선형 신호 흐름 그래프 모델의 예

• 일반적으로 고전 제어 이론 분석을 위해 시간 영역과 주파수 영역 표현 사이에서 변환할 수 없지만 비선형 신호 흐름 그래프는 전기 공학 문헌에서 찾을 수 있습니다.^[57][58]
• 비선형 신호 흐름 그래프는 생명과학에서도 찾아볼 수 있는데, 예를 들어 아서 가이튼 박사의 심혈관계 모델이 이에 해당합니다.^[59]

과학의 다양한 분야에서 SFG 기법의 적용

• 전자회로
  • 무어 및 멜리 타입의 순차 회로를 특징으로 하며, 상태 다이어그램으로부터 정규 표현식을 얻는 방법.^[60]
  • 비선형 데이터 변환기의^[58] 합성
  • 제어 및 네트워크 이론
  • 확률적 신호 처리.^[61]
  • 전자시스템의^[62] 신뢰성
• 생리학과 생물물리학
  • 심박출량 조절^[63]
• 시뮬레이션
  • 아날로그 컴퓨터에서의^[64] 시뮬레이션
• 신경과학과 조합학
  • 폴리크로니시의^[65] 연구

참고 항목

• 점근 이득 모형
• 본드그래프
• 코트 그래프
• 제어 시스템 위키북의 제어 시스템/신호 흐름 다이어그램
• 플로우 그래프(수학)
• 신호 흐름 그래프를 사용한 필터 설계 예제를 위한 도약대 필터
• 메이슨 이득 공식
• 마이너 루프 피드백
• 비상호적 신호 흐름 그래프

메모들

참고문헌

• Ernest J. Henley & R. A. Williams (1973). Graph theory in modern engineering; computer aided design, control, optimization, reliability analysis. Academic Press. ISBN 978-0-08-095607-7. 이 주제에 거의 전적으로 전념하는 책.
• Kou, Benjamin C. (1967), Automatic Control Systems, Prentice Hall
• Robichaud, Louis P.A.; Maurice Boisvert; Jean Robert (1962). Signal flow graphs and applications. Prentice-Hall electrical engineering series. Englewood Cliffs, N.J.: Prentice Hall. pp. xiv, 214 p.
• Deo, Narsingh (1974), Graph Theory with Applications to Engineering and Computer Science, PHI Learning Pvt. Ltd., p. 418, ISBN 978-81-203-0145-0
• K Thulasiramen; MNS Swarmy (2011). "§6.11 The Coates and Mason graphs". Graphs: Theory and algorithms. John Wiley & Sons. pp. 163 ff. ISBN 9781118030257.
• Ogata, Katsuhiko (2002). "Section 3-9 Signal Flow Graphs". Modern Control Engineering 4th Edition. Prentice-Hal. ISBN 978-0-13-043245-2.
• © Phang, Khoman (2000-12-14). "2.5 An overview of Signal-flow graphs" (PDF). CMOS Optical Preamplifier Design Using Graphical Circuit Analysis (Thesis). Department of Electrical and Computer Engineering, University of Toronto. 판권: Khoman Phang 2001

더보기

• Wai-Kai Chen (1976). Applied Graph Theory. North Holland Publishing Company. ISBN 978-0720423624. 3장은 필수 항목이지만, 신청서는 책 전체에 흩어져 있습니다.
• Wai-Kai Chen (May 1964). "Some applications of linear graphs". Contract DA-28-043-AMC-00073 (E). Coordinated Science Laboratory, University of Illinois, Urbana. Archived from the original on January 10, 2015.
• K. Thulasiraman & M. N. S. Swamy (1992). Graphs: Theory and Algorithms. John Wiley & Sons. 6.10-6.11 for the essential mathematical idea. ISBN 978-0-471-51356-8.
• Shu-Park Chan (2006). "Graph theory". In Richard C. Dorf (ed.). Circuits, Signals, and Speech and Image Processing (3rd ed.). CRC Press. § 3.6. ISBN 978-1-4200-0308-6. Mason과 Coates 그래프 접근법을 Maxwell의 k-tree 접근법과 비교합니다.
• RF Hoskins (2014). "Flow-graph and signal flow-graph analysis of linear systems". In SR Deards (ed.). Recent Developments in Network Theory: Proceedings of the Symposium Held at the College of Aeronautics, Cranfield, September 1961. Elsevier. ISBN 9781483223568. Coates 흐름 그래프와 Mason 흐름 그래프의 효용 비교.

외부 링크

• M. L. Edwards: S-parameter, 신호 흐름 그래프 및 기타 행렬 표현 All Rights Reserved
• H 슈미드: 12개의 짧은 강의에서 신호 흐름 그래프
• Wikibooks의 제어 시스템/신호 흐름 다이어그램
• Wikimedia Commons의 신호 흐름 그래프와 관련된 미디어