평행 곡선

곡선의 평행은 곡선을 중심으로 한 일치 원 계열의 외피다. 평행(직선)의 개념을 일반화한다. 또한 특정 곡선에서 일정한 정규 거리에 있는 점을 갖는 곡선으로 정의할 수 있다.^[1] 이 두 가지 정의는 후자가 부드러움을 가정하는 것과 완전히 동등하지는 않지만, 전자는 그렇지 않다.^[2]

컴퓨터 지원 설계에서 병렬 곡선의 선호 용어는 오프셋 곡선이다.^[2][3][4] (다른 기하학적 맥락에서 오프셋이라는 용어는 번역도 참조할 수 있다.)^[5] 오프셋 곡선은 예를 들어 2축 기계의 원형 절삭 공구에 의한 절삭의 형태를 설명하는 수적으로 제어되는 가공에서 중요하다. 절단부의 형태는 절단기의 궤적에서 정상 방향으로 일정한 거리에 의해 모든 지점에서 절단기의 궤적으로 상쇄된다.^[6]

벡터 그래픽으로 알려진 2D 컴퓨터 그래픽 영역에서 병렬 곡선의 (대략) 계산은 스트로킹이라고 하는 기본적인 그리기 작업 중 하나에 관여하는데, 일반적으로 이 작업은 그 분야의 폴리라인이나 폴리베지어(그들 자신이 경로라고 부르는 것)에 적용된다.^[7]

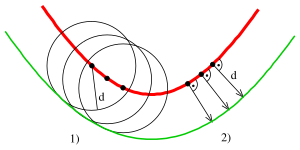
선이나 원의 경우를 제외하면 평행곡선은 선조체 곡선보다 수학적 구조가 더 복잡하다.^[1] 예를 들어, 선조체 곡선이 부드럽더라도 그 오프셋은 그렇지 않을 수 있다. 이 특성은 사인 곡선을 선조체 곡선으로 사용하여 상단 그림에 표시된다.^[2] 일반적으로 곡선이 합리적이더라도 상쇄는 그렇지 않을 수 있다. 예를 들어 포물선의 간격띄우기는 이성적인 곡선이지만 타원이나 하이퍼볼라의 간격띄우기는 이러한 선조체 곡선 자체가 이성적이기는 하지만 합리적이지 않다.^[3]

이 개념은 또한 3D 표면으로 일반화되는데, 여기서 오프셋 표면 또는 평행 표면이라고 불린다.^[8] 솔리드 볼륨을 (일정적) 거리 오프셋에 의해 증가시키는 것을 확장이라고도 한다.^[9] 반대작전을 포격이라고 부르기도 한다.^[8] 오프셋 표면은 3축 기계의 볼 노즈 엔드 밀에 의해 절단된 모양을 설명하는 수치로 제어되는 가공에서 중요하다.^[10] 다른 형태의 절단 비트는 일반적인 오프셋 표면으로 수학적으로 모델링할 수 있다.^[11]

모수적으로 주어진 곡선의 평행 곡선

${\displaystyle \mathrm{주어진}}$ 곡선의 정규$$ 파라메트릭 표현 $x{\displaystyle \stackrel{}{}}$→${\displaystyle }$=${\displaystyle }$( ${\displaystyle x}$(${\displaystyle }$)${\displaystyle }$, y ( )$displaystyle {\vec{x}=(x(t),y(t)}}}$이(가) 있는 경우, 평행 곡선(위의 두 번째 정의)은 ${\displaystyle 거리}$ d $displaysty d}$을(으)로 평행 곡선의 다음과 같은 파라메트릭 표현으로 이어진다$.$

${\displaystyle {\stackrel{}{x}}_{}}$${\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle d_{}}$ (${\displaystyle {}_{}}$t${\displaystyle }$)${\displaystyle }$= x${\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle t\stackrel{}{}}$) + ${\displaystyle d\stackrel{}{}}$n →${\displaystyle }$( ${\displaystyle t}$) ${\displaystyle {\vec{x}_{d}(t)={\vec{x$}(t$)+d{\$$vec{n}}(t$ $normal{\displaystyle \stackrel{}{}}$ n${\displaystyle \stackrel{}{}}$→ $)$ 단위$.$

데카르트 좌표에서:

${\dplaystyle x_{d}(t)=x(t)+{\frac {d\;y'(t)}{\sqrt{x'(t)^{2}+y'^{2}}}$

${\dplaystyle y_{d}(t)=y(t)-{\frac {d\;x'(t)}{\sqrt {x'(t)^{2}+y'^{2}}\ .}$

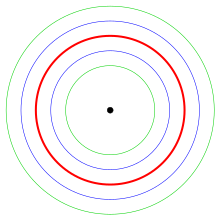
거리 매개 변수 $d{\displaystyle }$ ${\displaystyle d}$도 음수일 수 있다$$. 이 경우 곡선 반대편에 평행 곡선이 생긴다(원 평행 곡선의 도표 참조). 쉽게 확인할 수 있는 것은 선의 평행곡선은 상식적으로 평행선이고 원의 평행곡선은 동심원이다.

기하학적 특성:^[12]

• ${\displaystyle {\stackrel{}{x}}_{}^{}}$${\displaystyle {\stackrel{}{}}_{}^{}}$→ ${\displaystyle d_{}^{}}$ ${\displaystyle {}_{}^{}}$( t${\displaystyle }$)${\displaystyle {\stackrel{}{\to }}^{}}$ ${\displaystyle {\stackrel{}{}}^{}}$→${\displaystyle t}$ (${\displaystyle }$t ${\displaystyle )}$ , ${\$d}($t)\property {\vec{x}'(t),\properties$}: 고정 파라미터의 접선 벡터는 평행이다.
• ${\displaystyle k_{d}(t)={\frac {k(t)}{1+dk(t)}},\quad }$ with ${\displaystyle k(t)}$ the curvature of the given curve and ${\displaystyle k_{d}(t)}$ the curvature of the parallel curve for parameter ${\displaystyle t}$.
• ${\displaystyle R_{d}(t)=R(t)+d,\quad }$ with ${\displaystyle R(t)}$ the radius of curvature of the given curve and ${\displaystyle R_{d}(t)}$ the radius of curvature of the parallel curve for parameter ${\displaystyle t}$.
• 평행선의 경우, 곡선에 대한 정규선도 그 평행선과 정규선이다.
• 평행 곡선이 구성되면 곡선에서 거리가 곡률 반경과 일치할 때 쿠스가 생긴다. 곡선이 방아쇠에 닿는 지점들이다.
• 만약 선조체 곡선이 평면 세트의 경계이고 평행 곡선이 자기 교차점이 없는 경우, 후자는 평면 세트의 민코스키 합과 주어진 반지름의 원반이다.

주어진 곡선이 다항식($x{\displaystyle (t}$) ${\displaystyle x(t)}$ 및$$ $y{\displaystyle (t)}$ ${\displaystyle y(t)}$을(를) 다항식인 경우, 병렬 곡선은 일반적으로 다항식이 아니다. CAD 시스템에서는 다항식 또는 합리적인 곡선을 사용하기 때문에 CAD 영역에서는 단점이 있다. 최소한 합리적인 곡선을 얻기 위해서는 평행곡선 표현의 제곱근을 해결할 수 있어야 한다. 그러한 곡선은 피타고라스 호도 곡선이라고 불리며 R.T.파루키에 의해 조사되었다.^[13]

암묵적 곡선의 병렬 곡선

일반적으로 암묵적 곡선의 병렬 곡선의 분석적 표현은 불가능하다. 선과 원의 단순한 사례에 대해서만 평행 곡선을 쉽게 설명할 수 있다. 예를 들면 다음과 같다.

Line ${\displaystyle \;f(x,y)=x+y-1=0\;}$ → distance function: ${\displaystyle \;h(x,y)={\frac {x+y-1}{\sqrt {2}}}=d\;}$ (Hesse normalform)

Circle ${\displaystyle \;f(x,y)=x^{2}+y^{2}-1=0\;}$ → distance function: ${\displaystyle \;h(x,y)={\sqrt {x^{2}+y^{2}}}-1=d\;.$$}$

일반적으로 특정 조건을 가정하면 방향 거리 함수 $h{\displaystyle }$(${\displaystyle }$x ,${\displaystyle y}$) ${\displaystyle h(x,y)}$의 존재를 증명할 수 있다$.$실제로 숫자적으로 취급해야 한다.^[14] 병렬 곡선을 고려할 때 다음이 참이다.

• 거리 d에 대한 평행 곡선은 해당 방향 거리 $함수{\displaystyle }$ h$${\$displaystyle$ h$(x,y)=d}$의 레벨 $설정{\displaystyle }$ h${\displaystyle (x}$,y${\displaystyle }$) = d ${\$$displaystyle h}$이다$.$

거리 함수의 속성:^[12][15]

• ${\displaystyle \cHBName {x} =1\;,}$
• ${\displaystyle h({\vec{x}+d\d\benname {grad}\bec {x})=h({\vec {x}+d\;,}$
• ${\displaystyle \chdname {x}+d\prodname {grad}hp\vec {x})=\dradname {grad}h\\vec{x})\;}$

예:
다이어그램은 ${\displaystyle 방정식}$ f${\displaystyle (x}$ ,${\displaystyle y}$) = ${\displaystyle {}^{}{4\mathrm{}}^{}}$ + ${\displaystyle {}^{}{4\mathrm{}}^{}}$ -${\displaystyle 1}$ = 0$.$ {\$displaystyle$\;$f(x,y)=x^{4}+y^{4}-1=0\;$가 포함된 암묵적 곡선의 평행 곡선을 보여준다.$}$
Remark: The curves ${\displaystyle \;f(x,y)=x^{4}+y^{4}-1=d\;}$ are not parallel curves, because ${\displaystyle \; \operatorname {grad} f(x,y) =1\;}$ is not true in the area of interest.

추가 예

• 주어진 곡선의 비자발성은 평행곡선의 집합이다. 예를 들어, 원의 비자발성은 평행 나선형이다(도표 참조).

그리고:^[16]

• 포물선은 6도의 합리적인 곡선을 상쇄한다.
• 하이퍼볼라 또는 타원은 (양면)도 8의 대수 곡선을 상쇄한다.
• 정도 n의 베지어 곡선은 (양측)도 4n - 2의 대수적 곡선을 상쇄한다. 특히 입방형 베지어 곡선은 (양면) 대수적 곡선이 10도 정도로 상쇄된다.

모서리가 있는 곡선과 평행 곡선

가공을 위한 날카로운 모서리가 있는 부품의 절단 경로를 결정할 때, 모서리에 불연속 정규 분포를 갖는 주어진 곡선에 평행(오프셋) 곡선을 정의해야 한다. 주어진 곡선이 급커브에서 매끄럽지 않더라도 평행곡선은 연속적인 정상으로 매끄러울 수 있고, 또는 급커브에서 거리가 급커브 곡률 반경과 일치할 때 쿠스가 있을 수 있다.

일반 선풍기

위에서 설명한 대로 거리 ${\displaystyle d}$ $dapplaystyle$ ${\vec}{d}(t$에 대한 병렬 곡선 $x{\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle d_{}}$${\displaystyle (}$$t$$){\$$displaystyle {\vec}(t)$의 파라메트릭 $표현$은 다음과 같다$$$.$

${\displaystyle {\stackrel{}{x}}_{}}$${\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle d_{}}$ (${\displaystyle {}_{}}$t${\displaystyle }$)${\displaystyle }$= x${\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle t\stackrel{}{}}$) + ${\displaystyle d\stackrel{}{}}$n →${\displaystyle }$( ${\displaystyle t}$) ${\displaystyle {\vec{x}_{d}(t)={\vec{x$}(t$)+d{\$$vec{n}}(t$ $normal{\displaystyle \stackrel{}{}}$ n${\displaystyle \stackrel{}{}}$→ $)$ 단위$.$

At a sharp corner (${\displaystyle t=t_{c}}$), the normal to ${\displaystyle {\vec {x}}(t_{c})}$ given by ${\displaystyle {\vec {n}}(t_{c})}$ is discontinuous, meaning the one-sided limit of the normal from the left ${\displaystyle {\vec {n}}(t_$${c}^{-}}$은(는) $오른쪽{\displaystyle \stackrel{}{}}$ n${\displaystyle \stackrel{}{}}$→${\displaystyle }$( ${\displaystyle t_{}^{}}$ c${\displaystyle {}_{}^{}}$+${\displaystyle {}_{}^{}}$) ${\displaystyle {\vec{n}}(t_{c}^{+})$의 제한과 동일하지 않다$$$.$ 수학적으로,

${\displaystyle {\vec {n}}(t_{c}^{-})=\lim _{t\to t_{c}^{-}}{\vec {n}}(t)\neq {\vec {n}}(t_{c}^{+})=\lim _{t\to t_{c}^{+}}{\vec {n}}(t)}$.

하지만, 우리는({\displaystyle{\vec{n}}_ᆱ(\alpha)}는 n→(tc−){\displaystyle{\vec{n}}(t_{c}^{-})}과 n→(t댁+){\displaystyle{\vec{n}}(t_{c}^{+})}사이에 interpolant를 제공하고 n→ f(α)를 사용하{\displaystyle{\v 평범한 fan[11]n→ f 할 수 있다.ec{$n$$$$}_{f}(\f$})(\c$)$ 대신$$ 날카로운 모서리에 있는 $n{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{\to }}$( ${\displaystyle {}_{}}$ ${\displaystyle c_{}}$) ${\displaystyle {\vec{n}(t_{c}):$

${\displaystyle {\vec {n}}_{f}(\alpha )={\frac {(1-\alpha ){\vec {n}}(t_{c}^{-})+\alpha {\vec {n}}(t_{c}^{+})}{\lVert (1-\alpha ){\vec {n}}(t_{c}^{-})+\alpha {\vec {n}}(t_{c}$$^{+}\rVert },\quad }$ 여기서 << $<<\displaystyle$0$<\alpha <1}.$

병렬 곡선 $x{\displaystyle {\stackrel{}{}}_{}}$→ d (${\displaystyle {}_{}t}$) ${\displaystyle {\vec {x}_{d}(t)}$의 결과 정의는 원하는 동작을 제공한다$$.

${\displaystyle {\vec {x}}_{d}(t)={\begin{cases}{\vec {x}}(t)+d{\vec {n}}(t),&{\text{if }}t<t_{c}{\text{ or }}t>t_{c}\\{\vec {x}}(t_{c})+d{\vec {n}}_{f}(\alpha ),&{\text{if }}t=t_{c}{\text{ where }}0<\alpha <1\end{cases}}}$

알고리즘

이 구간은 확장이 필요하다. 덧셈으로 도와줘도 된다. (2014년 8월)

상쇄를 위한 효율적인 알고리즘은 키멜과 브루크슈타인(1993)이 기술한 레벨 어프로치다. ^[17]

이 문제에는 수많은 근사 알고리즘이 있다. 1997년 조사는 Elber, Lee 및 Kim의 "비교 간격띄우기 곡선 근사법"^[18]을 참조하십시오.

평행(오프셋) 표면

오프셋 표면은 3축 밀의 볼 노즈 엔드 밀에 의해 절단된 모양을 설명하는 수치 제어 가공에서 중요하다.^[10] If there is a regular parametric representation ${\displaystyle {\vec {x}}(u,v)=(x(u,v),y(u,v),z(u,v))}$ of the given surface available, the second definition of a parallel curve (see above) generalizes to the following parametric representation of the parallel surface with di${\displaystyle 스탠드}$ d $displaystyle d$

${\displaystyle {\vec {x}}_{d}(u,v)={\vec {x}}(u,v)+d{\vec {n}}(u,v)}$ with the unit normal ${\displaystyle {\vec {n}}_{d$$}}(u,v)={{{\cHB {\vec{x}} \over \cHB}\\cHB {\vc} \cHB {\c} \over \cHB}} \over$ \$cHB} \cHB$}}}}}} \over \cHB$\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}$

거리 매개 변수 $d{\displaystyle }$ ${\displaystyle d}$도 음수일 수 있다$$. 이 경우 표면의 반대쪽에 평행한 표면이 생긴다(원 평행 곡선의 유사한 도표 참조). 평면의 평행면은 상식적으로 평행면이고 구의 평행면은 동심구라는 것을 쉽게 확인할 수 있다.

기하학적 특성:^[19]

• ${\displaystyle {\partial {\vec {x}}_{d} \over \partial u}\parallel {\partial {\vec {x}} \over \partial u},\quad {\partial {\vec {x}}_{d} \over \partial v}\parallel {\partial {\vec {x}} \over \partial v},\quad }$ that means: t고정 매개변수에 대한 접선 벡터는 평행이다.
• ${\displaystyle {\stackrel{}{n}}_{}}$${\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle d_{}}$ (${\displaystyle u}$ , v )${\displaystyle }$=${\displaystyle }$± ${\displaystyle n\stackrel{}{}}$→ (${\displaystyle u}$, v${\displaystyle }$)${\displaystyle }$, ${\$),\$migration }:$ 고정 파라미터에 대한 일반 벡터는 방향과 일치한다.
• ${\displaystyle S_{d}=(1+dS)^{-1}S,\quad }$ where ${\displaystyle S_{d}}$ and ${\displaystyle S}$ are the shape operators for ${\displaystyle {\vec {x}}_{d}}$ and ${\displaystyle {\vec {x}}}$, respectively.

주 곡선은 형상 연산자의 고유값이며, 주 곡면 방향은 고유 벡터, 가우스 곡면성은 결정 요인, 평균 곡면성은 트레이스의 절반이다.

• ${\displaystyle S_{d}^{-1}=S^{-1}+dI,\quad }$ where ${\displaystyle S_{d}^{-1}}$ and ${\displaystyle S^{-1}}$ are the inverses of the shape operators for ${\displaystyle {\vec {x}}_{d}}$ and ${\displaystyle {\vec {x}}}$, respectively.

곡률의 주반경은 형상 연산자의 역의 고유값이며, 주곡률 방향은 고유 벡터, 가우스 곡률의 역수는 결정 요인, 평균 곡률 반경은 그 트레이스의 반이다.

병렬 곡선의 기하학적 특성과 유사성을 주목하십시오.

일반화

문제는 표면이 상쇄되는 경우와 같이 보다 높은 차원으로 상당히 명백하게 일반화되며 파이프 표면에는 약간 덜 사소한 문제가 일반화된다.^[20] 고차원 버전에 대한 용어는 평면의 경우보다 훨씬 더 다양하다는 점에 유의하십시오. 예를 들어 다른 저자들은 병렬 섬유, 리본 및 튜브를 언급한다.^[21] 3D 표면에 내장된 곡선의 경우 지오데틱을 따라 오프셋을 취할 수 있다.^[22]

이를 일반화하는 또 다른 방법은 (2D에서도) 가변 거리(예: 다른 곡선에 의해 파라메트리된)를 고려하는 것이다.^[19] 예를 들어, METAFONT에서 가능한^[19] 것처럼 원 대신 타원으로 스트로크(엔벨로브)를 할 수 있다.^[23]

보다 최근에 Adobe Illustrator는 가변 폭에 대한 제어 지점이 시각적으로 명시되어 있지만 버전 CS5에 다소 유사한 설비를 추가했다.^[24] 일정한 거리와 가변 거리를 구별하는 것이 중요한 맥락에서 CDO와 VDO의 두문자어 오프셋을 사용하는 경우가 있다.^[9]

일반 간격띄우기 곡선

Assume you have a regular parametric representation of a curve, ${\displaystyle {\vec {x}}(t)=(x(t),y(t))}$, and you have a second curve that can be parameterized by its unit normal, ${\displaystyle {\vec {d}}({\vec {n}})}$, where the normal of ${\displaystyle \overrightarrow{d}(\overrightarrow{n})=}$${\displaystyle \stackrel{}{n}}$→ ${\$정상에 의한 이 파라미터화는 곡선이 양 또는 음으로 엄격하게 볼록하고 매끄러우며 직선적이지 않은 곡선에 대해 존재한다. $x{\displaystyle \stackrel{}{}}$→${\displaystyle }$( ${\displaystyle t}$) ${\displaystyle {\vec{x}(t)}$ 오프셋$$ $by{\displaystyle \stackrel{}{}}$d${\displaystyle }$→ (${\displaystyle n\stackrel{}{}\stackrel{}{\to }}$ ) ${\displaystyle {\vec}({\vec{n})$의 일반 오프셋 곡선의 파라메트릭 표현은 다음과$$ 같다.

${\displaystyle {\vec {x}}_{d}(t)={\vec {x}}(t)+{\vec {d}}({\vec {n}}(t)),\quad }$ where ${\displaystyle {\vec {n}}(t)}$ is the unit normal of ${\displaystyle {\vec {x}}(t)}$.

trival 오프셋 $d{\displaystyle \stackrel{}{}}$→${\displaystyle }$( ${\displaystyle n\stackrel{}{}}$→${\displaystyle }$)${\displaystyle }$= ${\displaystyle d\stackrel{}{}}$ ${\displaystyle n\stackrel{}{}}$→ ${\$은$($는) 일반 평행(일명, 오프셋) 곡선을 제공한다는 점에 유의하십시오.

기하학적 특성:^[19]

• ${\displaystyle {\stackrel{}{x}}_{}^{}}$${\displaystyle {\stackrel{}{}}_{}^{}}$→ ${\displaystyle d_{}^{}}$ ${\displaystyle {}_{}^{}}$( t${\displaystyle }$)${\displaystyle {\stackrel{}{\to }}^{}}$ ${\displaystyle {\stackrel{}{}}^{}}$→${\displaystyle t}$ (${\displaystyle }$t ${\displaystyle )}$ , ${\$d}($t)\property {\vec{x}'(t),\properties$}: 고정 파라미터의 접선 벡터는 평행이다.
• 평행선의 경우, 곡선에 대한 정규 분포는 일반 간격띄우기에 대해서도 정규 분포를 따른다.
• ${\displaystyle k_{d}(t)={\dfrac {k(t)}{1+{\dfrac {k(t)}{k_{n}(t)}}}},\quad }$ with ${\displaystyle k_{d}(t)}$ the curvature of the general offset curve, ${\displaystyle k(t)}$ the curvature of ${\displaystyle {\vec$$$$\{$$x}}($$t$$)$ 및 $k{\displaystyle {}_{}t}$ ${\displaystyle )}$ ${\displaystyle k_{n}($${\displaystyle t}$$)}$ 매개 변수 ${\d$$}({\vec{n})(t)$에 $대한$ d${\displaystyle \stackrel{}{}}$→${\displaystyle }$( ${\displaystyle n\stackrel{}{}}$→${\displaystyle }$( $d)}$의 곡률$$.
• $R$$R_{n}(t),\quad }$ with ${\displaystyle R_{d}(t)}$ the radius of curvature of the general offset curve, ${\displaystyle R(t)}$ the radius of curvature of ${\displaystyle {\vec {x}}(t)}$, and ${\displaystyle R_{n}(t)}$ the radius of curvature of ${\displaystyle \overrightarrow{d}(\overrightarrow{n}(}$${\displaystyle t}$) ${\displaystyle {\vec}({\vec{n})(t)}$ 매개$$ 변수 $t{\displaystyle }$ ${\displaystyle t}$.
• 일반 오프셋 곡선이 생성되면 곡선의 곡면성이 오프셋의 곡률과 일치할 때 큐스가 생긴다. 곡선이 방아쇠에 닿는 지점들이다.

일반 간격띄우기 표면

일반적인 오프셋 표면은 3축 엔드 밀이 수적으로 제어되는 가공에서 사용하는 다양한 절단 비트에 의해 만들어진 절단 형태를 설명한다.^[11] Assume you have a regular parametric representation of a surface, ${\displaystyle {\vec {x}}(u,v)=(x(u,v),y(u,v),z(u,v))}$, and you have a second surface that can be parameterized by its unit normal, ${\displaystyle {\vec {d}}({\vec {n}})}$, where $d{\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle n\stackrel{}{}}$→${\displaystyle }$)${\displaystyle }$= n${\displaystyle \stackrel{}{}}$→ ${\displaystyle n\stackrel{}{}}$ →$${\$displaystyle${\$vec{d}({\vec{$n}}}={\$vec{$n}}}의 정규 분포는 가우스 곡률이 엄격히 양성이므로 볼록하고 매끈하며 평탄하지 않은 표면에 대해 존재한다.$$ $x{\displaystyle \stackrel{}{}}$→${\displaystyle }$( ${\displaystyle t}$) ${\displaystyle {\vec{x}(t)}$ 오프셋$$ $by{\displaystyle \stackrel{}{}}$d${\displaystyle }$→ (${\displaystyle n\stackrel{}{}\stackrel{}{\to }}$ ) ${\displaystyle {\vec}({\vec{n})$의 일반 오프셋 표면의 파라메트릭 표현은 다음과$$ 같다.

${\displaystyle {\vec {x}}_{d}(u,v)={\vec {x}}(u,v)+{\vec {d}}({\vec {n}}(u,v)),\quad }$ where ${\displaystyle {\vec {n}}(u,v)}$ is the unit normal of ${\displaystyle {\vec {x}}(u,v)}$.

trival 오프셋 $d{\displaystyle \stackrel{}{}}$→${\displaystyle }$( ${\displaystyle n\stackrel{}{}}$→${\displaystyle }$)${\displaystyle }$= ${\displaystyle d\stackrel{}{}}$ ${\displaystyle n\stackrel{}{}}$→ ${\$은$($는) 일반 평행(일명, 오프셋) 표면을 제공한다는 점에 유의하십시오.

기하학적 특성:^[19]

• 평행선의 경우, 표면의 접선면은 일반 간격띄우기의 접선면과 평행하다.
• 평행선의 경우, 표면에 대한 정규 분포도 일반적인 오프셋에 대해 정규 분포를 따른다.
• ${\displaystyle S_{d}=(1+SS_{n}^{-1})^{-1}S,\quad }$ where ${\displaystyle S_{d},S,}$ and ${\displaystyle S_{n}}$ are the shape operators for ${\displaystyle {\vec {x}}_{d},{\vec {x}},}$ and ${\disp$$레이스타일 {\vec{d}({\vec{n}})},$ 각각$.$

주 곡선은 형상 연산자의 고유값이며, 주 곡면 방향은 고유 벡터, 가우스 곡면성은 결정 요인, 평균 곡면성은 트레이스의 절반이다.

• ${\displaystyle S_{d}^{-1}=S^{-1}+S_{n}^{-1},\quad }$ where ${\displaystyle S_{d}^{-1},S^{-1}}$ and ${\displaystyle S_{n}^{-1}}$ are the inverses of the shape operators for ${\displaystyle {\vec {x}}_{d},{\vec {x$$}},},$ d${\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle n\stackrel{}{}}$→ )${\displaystyle {\vec{d}}({\vec{n}})},$ 각각$$$.$

곡률의 주반경은 형상 연산자의 역의 고유값이며, 주곡률 방향은 고유 벡터, 가우스 곡률의 역수는 결정 요인, 평균 곡률 반경은 그 트레이스의 반이다.

일반 간격띄우기 곡선의 기하학적 특성과 유사성에 유의하십시오.

일반 간격띄우기에 대한 기하학적 특성 도출

일반 간격띄우기 곡선과 지표면에 대해 위에 나열된 기하학적 특성은 임의 치수의 간격띄우기에 대해 도출할 수 있다. $u{\displaystyle \stackrel{}{}}$ →${\$$x}({\vec$${u}})$의 치수가 n-1인$$ n-dension 표면, x →${\displaystyle \stackrel{}{}(u\stackrel{}{}}$→${\displaystyle }$) ${\displaystyle${\$vec${$u}}}}$의 정규 파라메트릭을 가지고 있다고 가정해 보십시오$.$ Also assume you have a second n-dimensional surface that can be parameterized by its unit normal, ${\displaystyle {\vec {d}}({\vec {n}})}$, where the normal of ${\displaystyle {\vec {d}}({\vec {n}})={\vec {n}}}$ (this parameterization by normal exists for surfaces whose Gaussi곡면성은 엄격히 양성이므로 볼록하고 매끄러우며 평탄하지 않다). $x{\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle u\stackrel{}{}}$→${\displaystyle }$) ${\displaystyle {\vec{x}({\vec{u}})}$ 오프셋을$$ $d{\displaystyle \stackrel{}{}}$→ ${\displaystyle (n\stackrel{}{}}$→$){\displaystyle {\vec}({\vec{n}})$로 나타내는 일반 오프셋 표면의 파라미터는 다음과 같다$$.

${\displaystyle {\vec {x}}_{d}({\vec {u}})={\vec {x}}({\vec {u}})+{\vec {d}}({\vec {n}}({\vec {u}})),\quad }$ where ${\displaystyle {\vec {n}}({\vec {u}})}$ is the unit normal of ${\disp$$레이스타일 {{\vec{x}({\vec{u$ (트리벌 오프셋 $d{\displaystyle \stackrel{}{}}$→ ${\displaystyle (n\stackrel{}{}}$→${\displaystyle }$)${\displaystyle }$= ${\displaystyle dn\stackrel{}{}}$→ ${\dec{d}}({\vec{n$}})=$d{\$vec$\{$$n}}}})$는 일반적인 평행 표면을 제공한다.

$먼저{\displaystyle \stackrel{}{}}$ x${\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle u\stackrel{}{}}$→${\displaystyle }$)${\displaystyle }$= ${\displaystyle {\vec{x}({\vec{u}})=}$$d{\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle n\stackrel{}{}}$→ ${\displaystyle (u\stackrel{}{}}$→${\displaystyle }$)${\displaystyle }$= n${\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle u\stackrel{}{}}$→ ) = ${\displaystyle n\stackrel{}{}}$ → (u →${\displaystyle ),}$ ${\displaystyle{\vec{n}({\vec {u}})$의 정상임을$$ 주목한다.$={\vec{n}({\vec {u}),$ 정의상으로는$$} 이제 접선면에 걸쳐 접선 벡터를 주는 차동 w.r.t $u{\displaystyle \stackrel{}{}}$→ ${\$를${\displaystyle {\stackrel{}{}}_{}}$x → ${\displaystyle d_{}}$ ${\$에 적용하겠다$.$

${\displaystyle \c{x}_{d}({\vec{u}})=\property {\vec}{x}}({\vec {u})+\property {d}({\vec {n})({\vec {u})}}}}}}}}$

Notice, the tangent vectors for ${\displaystyle {\vec {x}}_{d}}$ are the sum of tangent vectors for ${\displaystyle {\vec {x}}({\vec {u}})}$ and its offset ${\displaystyle {\vec {d}}({\vec {n}})}$, which share the same unit normal. 따라서 일반 오프셋 표면은 $x{\displaystyle \stackrel{}{}}$→ ${\displaystyle (u\stackrel{}{}}$→${\displaystyle }$) ${\displaystyle {\vec}({\vec{u}})$ 및$$ $d{\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle n\stackrel{}{}}$→${\displaystyle }$(${\displaystyle u\stackrel{}{}}$→$){\vec {d}({\vec{n}})({\vec$ {u$}})}$과 동일한 접선면과 일반을 공유한다$.$ 그것은 봉투의 성격과 일치한다.

We now consider the Weingarten equations for the shape operator, which can be written as ${\displaystyle \partial {\vec {n}}=-\partial {\vec {x}}S}$. If ${\displaystyle S}$ is invertable, ${\displaystyle \partial {\vec {x}}=-\partial {\vec {n}}S^{-1}}$. Recall tats 표면의 주요 곡선은 형상 연산자의 고유값이고, 주 곡면 방향은 고유 벡터, 가우스 곡면성은 결정 요인, 평균 곡면성은 트레이스의 절반이다. 형상 연산자의 역행은 곡률 반경에 대해 이와 동일한 값을 갖는다.

$x{\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle d_{}}$ ${\$의 차등 방정식으로 대체하면 다음과 같은 결과를 얻을 수 있다$.$

${\displaystyle \partial {\vec {x}}_{d}=\partial {\vec {x}}-\partial {\vec {n}}S_{n}^{-1},\quad }$ where ${\displaystyle S_{n}}$ is the shape operator for ${\displaystyle {\vec {d}}({\vec {n}}({\vec {u}}))}$.

다음으로 $\partial {\displaystyle \mathrm{}n\stackrel{}{}}$→ ${\$:을(를) 교체하기 위해 Weingarten 방정식을 다시 사용한다.

${\$$SS_{n}^{-1},\quad }$ 여기서$$ $S{\displaystyle }$ ${\displaystyle S}$은(는) $x{\displaystyle \stackrel{}{}}$→${\displaystyle }$(${\displaystyle u\stackrel{}{}}$→${\displaystyle }$) ${\displaystyle {\bec{x}}({\vec {u}})}$의 형상 연산자 입니다$.$

${\displaystyle 그런\stackrel{}{}}$ 다음 $\partial {\displaystyle \mathrm{}}$ x${\displaystyle \stackrel{}{}}$→ ${\$에 대해 해결하고 -${\displaystyle S}$ ${\displaystyle -S}$을(를) 사용하여 Weingarten 방정식으로 되돌리는데, 이번에는 $\partial {\displaystyle \mathrm{}}$ ${\displaystyle {\stackrel{}{}}_{}}$→ ${\displaystyle d_{}}$ ${\${\$x}_{d}$:

${\displaystyle \vec {x}_{d}(I+SS_{n}^{-1})^{-1}^{-1}=\partial {\vec {x},}$

${\displaystyle -\vec {x}_{d}(I+SS_{n}^{-1})^{-1}S=-\vec{x}S=\partial {\vec {n}.}$

Thus, ${\displaystyle S_{d}=(I+SS_{n}^{-1})^{-1}S}$, and inverting both sides gives us, ${\displaystyle S_{d}^{-1}=S^{-1}+S_{n}^{-1}}$.

참고 항목

• 범프 매핑
• 거리함수 및 서명거리함수
• 거리장
• 오프셋 인쇄
• 관형근린

참조

• Josef Hoschek: 평면의 간격띄우기 곡선. In: CAD. 17 (1985), S. 77–81.
• 마에카와 다카시: 간격띄우기 곡선과 지표면의 개요. In: CAD.31 (1999), S. 165–173.

추가 읽기

• Farouki, R. T.; Neff, C. A. (1990). "Analytic properties of plane offset curves". Computer Aided Geometric Design. 7 (1–4): 83–99. doi:10.1016/0167-8396(90)90023-K.
• Piegl, Les A. (1999). "Computing offsets of NURBS curves and surfaces". Computer-Aided Design. 31 (2): 147–156. CiteSeerX 10.1.1.360.2793. doi:10.1016/S0010-4485(98)00066-9.
• Porteous, Ian R. (2001). Geometric Differentiation: For the Intelligence of Curves and Surfaces (2nd ed.). Cambridge University Press. pp. 1–25. ISBN 978-0-521-00264-6.
• Patrikalakis, Nicholas M.; Maekawa, Takashi (2010) [2002]. Shape Interrogation for Computer Aided Design and Manufacturing. Springer Science & Business Media. Chapter 11. Offset Curves and Surfaces. ISBN 978-3-642-04074-0. 무료 온라인 버전.
• Anton, François; Emiris, Ioannis Z.; Mourrain, Bernard; Teillaud, Monique (May 2005). "The O set to an Algebraic Curve and an Application to Conics". International Conference on Computational Science and its Applications. Singapore: Springer Verlag. pp. 683–696.
• Farouki, Rida T. (2008). Pythagorean-Hodograph Curves: Algebra and Geometry Inseparable. Springer Science & Business Media. pp. 141–178. ISBN 978-3-540-73397-3. 열거된 페이지들은 일반 자료와 소개 자료들이다.
• Au, C. K.; Ma, Y.-S. (2013). "Computation of Offset Curves Using a Distance Function: Addressing a Key Challenge in Cutting Tool Path Generation". In Ma, Y.-S. (ed.). Semantic Modeling and Interoperability in Product and Process Engineering: A Technology for Engineering Informatics. Springer Science & Business Media. pp. 259–273. ISBN 978-1-4471-5073-2.

외부 링크

• MathWorld의 병렬 곡선
• 평면 곡선 시각 사전 자 리
• http://library.imageworks.com/pdfs/imageworks-library-offset-curve-deformation-from-Skeletal-Anima.pdf에서 애니메이션으로 응용 프로그램, http://www.google.com/patents/US8400455으로 특허 획득
• http://www2.uah.es/fsegundo/Otros/Offset/16-SanSegundoSendraSendra-1532.pdf