광학적 소용돌이

Optical vortex
다양한 모드의 다이어그램, 그 중 4개는 광학 vortces이다. 기둥은 보의 나선 구조, 위상-전면 및 강도를 보여준다.

광학적 소용돌이(광학적 양자 소용돌이, 나사 탈구 또는 위상 특이점이라고도 함)는 광학장의 영점이며, 0 강도의 지점이다. 이 용어는 또한 그 안에 그러한 0이 있는 빛의 빔을 묘사할 때 사용된다. 이러한 현상에 대한 연구는 단수 광학이라고 알려져 있다.

설명

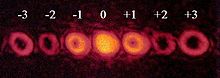
광학적 소용돌이 속에서 빛은 코르크따개처럼 그것의 이동 축을 중심으로 꼬인다. 비틀림 때문에 축의 광파 자체가 서로를 상쇄한다. 평평한 표면에 투영될 때 광학적 소용돌이는 빛의 고리처럼 생겼고, 중앙에 어두운 구멍이 있다. 어둠이 중심에 있는 이 빛의 코르크 마개를 광학적 소용돌이라고 부른다. 이 소용돌이는 빛이 한 파장에서 얼마나 많은 반전을 하느냐에 따라 위상학적 전하라고 불리는 숫자를 부여받는다. 숫자는 항상 정수로, 트위스트의 방향에 따라 양수 또는 음수가 될 수 있다. 트위스트 횟수가 많을수록 조명이 축을 중심으로 빠르게 회전하고 있다.

이 회전은 파동 열차에 궤도 각운동량을 전달하며, 전기 쌍극자의 토크를 유도한다. 궤도 각도 운동량은 더 흔히 마주치는 회전 각도 운동량과 구별되며, 이는 원형 양극화를 생성한다.[1] 빛의 궤도 각도 운동량은 갇힌 입자의 궤도 운동에서 관찰할 수 있다. 광학적 소용돌이를 빛의 평면 파동으로 방해하면 나선상이 동심원 나선형으로 나타난다. 나선형의 팔의 수는 위상학적 전하와 같다.

광학 vortices는 다양한 방법으로 연구실에서 만들어진다. 그것들은 레이저에서 직접 생성될 수도 있고,[2][3] 레이저 빔은 컴퓨터 생성 홀로그램, 나선상 지연 구조물, 또는 재료의 바이어프링턴트 포트리스와 같은 몇 가지 방법 중 하나를 사용하여 소용돌이로 꼬일 수도 있다.

특성.

광학 특이점은 광학장의 0이다. 필드의 위상은 이러한 제로 강도(이름 소용돌이)를 중심으로 순환한다. vortices는 2D 필드의 점이며 3D 필드의 선입니다(코디멘션 2가 있기 때문에). 소용돌이를 둘러싸는 경로 주위에 필드의 위상을 통합하면 2㎛의 정수 배수가 발생한다. 이 정수는 소용돌이의 위상학적 전하 또는 강도로 알려져 있다.

초지하학-가우스 모드(HyGG)는 중심에 광학적 소용돌이가 있다. 그 형태를 가진 빔은

베셀 함수로 구성된 근축파 방정식(근축 근사 및 실제 방정식에 대한 푸리에 광학 기사 참조)에 대한 해법이다. 초지하학-가우스 빔의 광자는 궤도 각도 운동량이 m³이다. 정수 m은 또한 빔의 중심에 있는 소용돌이의 강도를 제공한다. 원형으로 편광된 빛의 스핀 각도 운동량은 궤도 각도 운동량으로 변환할 수 있다.[4]

창조

나선 위상 플레이트, 컴퓨터 생성 홀로그램, 모드 변환, q 플레이트 또는 공간 광 변조기를 포함한 초지하학-가우스 모드를 만드는 몇 가지 방법이 존재한다.

  • 정적 나선상 플레이트(SPP)는 나선형 모양의 결정체나 플라스틱 조각으로, 원하는 위상학적 전하와 입사 파장에 맞게 특별히 설계된다. 그것들은 효율적이지만 비싸다. 조절 가능한 SPP는 금이 간 플라스틱 조각의 양면 사이에서 쐐기를 움직여 만들 수 있다.
  • 컴퓨터 생성 홀로그램(CGHs)은 평면 파동과 필름으로 전송되는 라구에르-가우스 빔 사이의 계산된 인터페로그램이다. CGH는 일반적인 Ronchi 선형 회절 격자를 닮아 "fork" 탈구를 구한다. 입사 레이저 빔은 토폴로지 전하가 회절 순서에 따라 증가하는 보티스로 회절 패턴을 생성한다. 제로 순서는 가우스어(Gaussian)이며, 이 굴절되지 않은 빔의 양쪽에 반대쪽 나선성이 있다. CGH 포크의 prong 수는 첫 번째 회절 순서 소용돌이의 위상학적 전하와 직접적인 관련이 있다. CGH는 첫 번째 순서에 더 강렬하게 지시하기 위해 맹렬히 사용될 수 있다. 표백은 그것을 강도의 그래팅에서 위상 그래팅으로 변화시켜 효율을 높인다.
CGH에 의해 생성된 포트
  • 모드 전환에는 헤르미테-가우스(HG) 모드가 필요하며, 레이저 캐비티 내부 또는 외부적으로는 덜 정확한 방법으로 쉽게 만들 수 있다. 난시 렌즈 한 쌍은 입력 HG에 따라 방위각과 방사형 지수로 LG 빔을 생성하는 구이 위상 시프트를 도입한다.
  • 공간광 변조기는 컴퓨터로 제어되는 전자 액정 소자로 굴절률의 홀로그램을 만들어 역동적인 배관, 배관 등 다양한 종류의 빔을 만들 수 있다.[5] 이 홀로그램은 포크 패턴, 나선형 위상 플레이트 또는 0이 아닌 위상학적 전하를 가진 유사한 패턴일 수 있다.
  • 세그먼트로 만들어진 변형 가능한 거울은 고출력 레이저로 조명을 받더라도 동적으로(최대 몇 kHz의 속도로) vorticle을 생성하는데 사용할 수 있다.
  • q플레이트는 국소 광학 축의 방위 분포를 갖는 2중환 액정 플레이트로, 중심 결함에 위상 전하 q가 있다. 위상 전하 q 플레이트는 입력 빔 양극화에 따라± 2 전하 소용돌이를 생성할 수 있다.
  • s-plate는 q-plate와 유사한 기술로, s의 위상 전하와 함께 고속 축의 방위 변동을 갖는 실리카 유리에 고강도의 UV 레이저를 사용하여 2차 유리의 패턴을 영구히 에칭한다. 액정 위의 바이어스 전압을 조정하여 파장을 조정할 수 있는 q 플레이트와 달리 s 플레이트는 빛의 한 파장에 대해서만 작동한다.
  • 무선 주파수에서 (비 광학) 전자기 소용돌이를 생성하는 것은 사소한 일이다. 안테나 1개 또는 더 큰 직경의 링을 단순히 배열하여 방송 안테나의 위상 편이가 링 주위로 2㎛의 적분 배수를 변화시키도록 한다.

탐지

근본적으로 위상 구조인 광학적 소용돌이는 그것의 강도 프로파일만으로는 감지할 수 없다. 또한 동일한 순서의 소용돌이 빔은 대략 동일한 강도 프로파일을 가지므로 강도 분포로만 특성화할 수 없다. 그 결과 광범위한 간섭 기법이 채용되고 있다.

  • 가장 간단한 기술은 소용돌이 빔을 기울어진 평면 파형으로 간섭하여 포크처럼 생긴 인터페로그램을 만드는 것이다. 패턴 내의 포크의 수와 그 상대적 방향을 세어 보면, 소용돌이 순서와 그에 상응하는 부호를 정확하게 추정할 수 있다.[6]
  • 볼텍스 빔은 기울어진 렌즈를 통과하는 동안 특유의 로브 구조로 변형될 수 있다. 이것은 소용돌이의 서로 다른 위상점들 사이의 자기 상호 작용의 결과로 일어난다. 순서 l의 소용돌이 빔은 기울어진 볼록렌즈의 초점 깊이를 중심으로 대략 n = l + 1 로브로 분할될 것이다. 또한 로브의 방향(우측 및 좌측 대각선)은 양의 궤도 각도 운동량 및 음의 각도 운동량 순서를 결정한다.[7]
  • 소용돌이 빔은 반대편 기호의 소용돌이를 방해할 때 로브 구조를 생성한다. 그러나 이 기법은 기호를 특징짓는 메커니즘을 제공하지 않는다. 이 기법은 볼텍스 프로필로 펌핑된 마하-젠더 간섭계의 경로 중 하나에 도브 프리즘을 배치하여 사용할 수 있다.[6]

적용들

통신과 이미징의 다양한 영역에서 광학 용도의 광범위한 응용이 있다.

  • 외행성은 모항성이 매우 밝기 때문에 최근에야 직접 검출되었다. 다른 기법으로 관측하기에는 부모 대비 대비 대비율이 너무 낮은 행성을 직접 관측할 수 있는 광학적 소용돌이 코로나그래프를 만드는 데 진전이 있었다.
  • 광학 보티스는 광학 핀셋에 사용되어 세포와 같은 마이크로미터 크기의 입자를 조작한다. 그러한 입자는 OAM을 사용하여 빔의 축을 중심으로 궤도로 회전할 수 있다. 광학적 소용돌이 핀셋을 이용한 마이크로 모터도 만들어졌다.
  • 광학 vortice는 통신 대역폭을 크게 개선할 수 있다. 예를 들어, 꼬인 라디오 빔은 많은 수의 vortical 상태를 사용함으로써 무선 스펙트럼 효율을 높일 수 있다.[8][9][10] 위상 전방의 '틀림' 양은 궤도 각도 모멘텀 상태 번호를 나타내며, 궤도 각도 모멘텀이 서로 다른 빔은 직교한다. 그러한 궤도 각도 운동량 기반 멀티플렉싱은 밀리미터파 무선 통신의 시스템 용량과 스펙트럼 효율을 잠재적으로 증가시킬 수 있다.[11]
  • 마찬가지로 광학 영역에서 궤도 각도 모멘텀 멀티플렉싱에 대한 초기 실험 결과는 단거리에서 결과를 보여주었지만,[12][13] 더 긴 거리 시연은 여전히 진행 중이다. 이러한 시연들이 직면한 가장 큰 도전은 기존의 광섬유가 번식할 때 보르티스의 스핀 각도 운동량을 변화시키고, 구부리거나 스트레스를 받을 때 궤도 각도 운동량을 변화시킬 수 있다는 것이다. 지금까지 특수 광섬유에서는 최대 50m의 안정적인 전파가 입증되었다.[14] 143 km의 거리에서 빛의 궤도 각도 운동 모드의 자유 공간 전송은 양호한 견고성으로 정보의 인코딩을 지원할 수 있다는 것이 입증되었다.[15]
  • 현재의 컴퓨터는 0과 1의 두 가지 상태를 가진 전자를 사용한다. 양자 컴퓨팅은 정보를 암호화하고 저장하기 위해 빛을 사용할 수 있다. 광학 vortices는 위상학적 전하에는 제한이 없기 때문에 이론적으로 자유 공간에 무한한 수의 상태를 가지고 있다. 이것은 더 빠른 데이터 조작을 가능하게 할 수 있다. 암호학계도 위에서 논의한 보다 높은 대역폭 통신의 약속에 대한 광학적 방편에 관심이 있다.
  • 광학 현미경에서는 광학 vorticles를 사용해 STED(Inspected Discovery Declosure) 현미경이라는 기법을 사용하여 정상적인 회절 한계를 넘어 공간 분해능을 달성할 수 있다. 이 기법은 빔 중앙의 특이점에서의 낮은 강도를 이용하여 원하는 표적 구역의 불소자를 고강도의 광학적 소용돌이 빔으로 원하는 구역 주변의 불소자를 고갈시키지 않는다.[16]
  • 광학 vortices는 또한 선형 또는 비선형 상호작용 방식에 따른 양자 vortices의 역학을 연구하기 위해 빛과 물질의 극지방 유체로 직접(전반적으로) 전달될 수 있다.[17]
  • 광학 vortices는 얽힌 광자 쌍의 국부적이지 않은 상관관계에서 식별할 수 있다.[18]

참고 항목

참조

  1. ^ Allen, L.; Beijersbergen, M. W.; Spreeuw, R. J. C.; Woerdman, J. P. (1992). "Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes". Phys. Rev. A. 45 (11): 8185–8189. Bibcode:1992PhRvA..45.8185A. doi:10.1103/PhysRevA.45.8185. PMID 9906912.
  2. ^ White, AG; Smith, CP; Heckenberg, NR; Rubinsztein-Dunlop, H; McDuff, R; Weiss, CO; Tamm, C (1991). "Interferometric measurements of phase singularities in the output of a visible laser". Journal of Modern Optics. 38 (12): 2531–2541. Bibcode:1991JMOp...38.2531W. doi:10.1080/09500349114552651.
  3. ^ Naidoo, Darryl; et al. (2016). "Controlled generation of higher-order Poincaré sphere beams from a laser". Nature Photonics. 10 (5): 327–332. arXiv:1505.02256. Bibcode:2016NaPho..10..327N. doi:10.1038/nphoton.2016.37. S2CID 7737430.
  4. ^ Marrucci, L.; Manzo, C; Paparo, D (2006). "Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media". Physical Review Letters. 96 (16): 163905. arXiv:0712.0099. Bibcode:2006PhRvL..96p3905M. doi:10.1103/PhysRevLett.96.163905. PMID 16712234. S2CID 15600569.
  5. ^ Heckenberg, NR; McDuff, R; Smith, CP; White, AG (1992). "Generation of optical phase singularities by computer-generated holograms" (PDF). Optics Letters. 17 (3): 221–223. Bibcode:1992OptL...17..221H. doi:10.1364/OL.17.000221. PMID 19784282.
  6. ^ a b Gbur, Greg (2015). "Singular Optics". The Optics Encyclopedia. Wiley. pp. 1–23. doi:10.1002/9783527600441.oe1011. ISBN 9783527600441.
  7. ^ Vaity, Pravin; Banerji, J.; Singh, R.P. (2013). "Measuring the topological charge of an optical vortex by using a tilted convex lens". Physics Letters A. 377 (15): 1154–1156. Bibcode:2013PhLA..377.1154V. doi:10.1016/j.physleta.2013.02.030. ISSN 0375-9601.
  8. ^ 뒤틀린 라디오 빔은 전파를 풀 수 있다.
  9. ^ 저주파 무선영역의 광자 궤도각운동량 활용에 관한 연구
  10. ^ 무선 vorticity를 통해 동일한 주파수의 많은 채널을 인코딩: 첫 번째 실험 테스트
  11. ^ Yan, Yan (16 September 2014). "High-capacity millimetre-wave communications with orbital angular momentum multiplexing". Nature Communications. 5: 4876. Bibcode:2014NatCo...5.4876Y. doi:10.1038/ncomms5876. PMC 4175588. PMID 25224763.
  12. ^ "'Twisted light' carries 2.5 terabits of data per second". BBC News. 2012-06-25. Retrieved 2012-06-25.
  13. ^ Bozinovic, Nenad (June 2013). "Terabit-Scale Orbital Angular Momentum Mode Division Multiplexing in Fibers". Science. 340 (6140): 1545–1548. Bibcode:2013Sci...340.1545B. doi:10.1126/science.1237861. PMID 23812709. S2CID 206548907.
  14. ^ Gregg, Patrick (January 2015). "Conservation of orbital angular momentum in air-core optical fibers". Optica. 2 (3): 267–270. arXiv:1412.1397. Bibcode:2015Optic...2..267G. doi:10.1364/optica.2.000267. S2CID 119238835.
  15. ^ Krenn, M; et al. (2016). "Twisted Light Transmission over 143 kilometers". PNAS. 113 (48): 13648–13653. arXiv:1606.01811. Bibcode:2016PNAS..11313648K. doi:10.1073/pnas.1612023113. PMC 5137742. PMID 27856744.
  16. ^ Yan, Lu (September 2015). "Q-plate enabled spectrally diverse orbital-angular-momentum conversion for stimulated emission depletion microscopy". Optica. 2 (10): 900–903. Bibcode:2015Optic...2..900Y. doi:10.1364/optica.2.000900. S2CID 52238379.
  17. ^ Dominici, L; Dagvadorj, G; Fellows, JM; et al. (2015). "Vortex and half-vortex dynamics in a nonlinear spinor quantum fluid". Science Advances. 1 (11): e1500807. arXiv:1403.0487. Bibcode:2015SciA....1E0807D. doi:10.1126/sciadv.1500807. PMC 4672757. PMID 26665174.
  18. ^ Gomes, R. M.; Salles, A.; Toscano, F.; Souto Ribeiro, P.H. (16 July 2009). "Observation of a Nonlocal Optical Vortex". Phys. Rev. Lett. 103 (3): 033602. arXiv:0902.1659. Bibcode:2009PhRvL.103c3602G. doi:10.1103/PhysRevLett.103.033602. PMID 19659278.

외부 링크