가우스 빔

TEM₀₀ 가우스 빔의 전계 진폭 실부의 순간 절대값, 초점 영역.

|{\mathcal {Re}}(E(t_{1}))|

e (

|{\mathcal {Re}}(E(t_{1}))|

(

|{\mathcal {Re}}(E(t_{1}))|

1)

|{\mathcal {Re}}(E(t_{1}))|

\

displaystyle

\

mathcal

{

Re}

（

|{\mathcal {Re}}(E(t_{1}))|

E

|{\mathcal {Re}}(E(t_{1}))|

（

|{\mathcal {Re}}(E(t_{1}))|

t

|{\mathcal {Re}}(E(t_{1}))|

_ { 1} ）

}

} 。각

|{\mathcal {Re}}(E(t_{1}))|

양의 파면마다 2개의 피크가 표시됩니다.

상단: 페이지 밖으로 전파되는 가우스 빔의 가로 강도 프로파일.파란색 곡선: 전기(또는 자기) 전계 진폭 대 빔 축으로부터의 반경 위치.검은색 곡선은 해당하는 강도입니다.

TEM 프로파일을₀₀ 나타내는 5mW 녹색 레이저 포인터 빔프로파일

광학에서 가우스 빔은 가우스 함수에 의해 가로 평면의 진폭 엔벨로프가 주어지는 높은 단색의 전자 방사 빔입니다. 이는 가우스 강도(방사조도) 프로파일을 의미하기도 합니다.이 기본(또는₀₀ TEM) 가로 방향 가우스 모드는 대부분의 (전부는 아니지만) 레이저의 의도된 출력을 나타냅니다.이러한 광선은 가장 집중된 지점에 초점을 맞출 수 있기 때문입니다.이러한 빔이 렌즈에 의해 다시 초점이 맞춰지면 횡단 위상 의존성이 변경되어 다른 가우스 빔이 생성됩니다.이러한 원형 가우스 빔(특정 파장 및 편광에 대한)에 따른 전기장 및 자기장 진폭 프로파일은 단일 파라미터, 이른바 $웨이스트 0$ w에 의해 결정됩니다.이것에 의해^[1], $소정$ 의₀ w를 가지는 빔을 따라서 허리(초점)에 상대하는 $임의$ 의 위치 z에서, 다음과 같이 필드 진폭과 위상이 결정된다.

아래 방정식은 z의 $모든$ 값에서 단면이 원형인 빔을 가정합니다. 이는 단일 횡단 치수 $r$ 이 나타나는 것을 보면 알 수 있습니다.단면이 타원형인 빔 또는 두 가로 치수(이상형 빔)에 대해 $z$ 의 다른 위치에 있는 웨이스트를 가진 빔은 가우스 빔으로도 설명할 수 있지만, 두 가로 $치수$ x 및 $y$ 에 대해 w 및 $z$ = $0$ $위치$ 의₀ 고유한 값을 가집니다.

근축 헬름홀츠 방정식의 임의 해는 에르미트-가우스 모드(직교 좌표를 사용하여 $x$ 와 $y$ 로 진폭 프로파일을 분리할 수 있음)의 조합 또는 라게르-가우스 모드(원통 ^[2]^[3]좌표를 사용하여 r과 $θ$ 로 진폭 프로파일을 분리할 수 있음)의 조합으로 표현할 수 있다. $빔$ z를 따라 있는 모든 지점에서 이러한 모드는 기본 가우스 모드와 동일한 가우스 계수를 포함하며 지정된 모드에 대한 추가 기하학적 계수를 곱합니다.그러나 다른 모드는 다른 Gouy 위상과 함께 전파되므로 모드의 중첩으로 인한 순 횡단 프로파일은 z $단위$ 로 진화하지만, 단일 Hermite-Gaush(또는 Laguerre-Gaush) 모드의 전파는 빔을 따라 동일한 형태를 유지합니다.

다른 가능한 모달 분해가 있지만, 이러한 솔루션 패밀리는 콤팩트 빔과 관련된 문제, 즉 광파워가 축을 따라 다소 좁혀지는 문제에 가장 유용합니다.레이저가 기본 가우스 모드로 동작하지 않는 경우에도 고차 모드의 공간적 범위가 레이저의 공진기(공진기)의 경계를 초과하는 경향이 있기 때문에 일반적으로 이러한 분해를 사용하여 가장 낮은 차수의 모드에서 레이저의 전력을 찾을 수 있습니다."가우스 빔"은 일반적으로 기본(TEM₀₀) 가우스 모드로 제한된 방사선을 의미합니다.

수학적 형식

w =

2µ

인₀ 가우스 빔 프로파일.

가우스 빔은 횡전자파([4]TEM) 모드입니다.전계 진폭의 수학식은 근축 헬름홀츠 ^[1]방정식의 해법입니다. $x방향$ 편광과 $+ z방향$ 전파를 가정할 때 위상(복소) 표기에서의 전계는 다음과 같습니다.

{\mathbf {E}(r,z)}=E_{0},{\hat {\mathbf {x}},{\frac {-leftf}{w(z)}}\exp \rc {-r^{2}}{-right}\exp \left(\xp)\xp \left(\ifrclef {\xp}{{\xp}{{{\xp}{\xp}{{{{\xp}}{{{{{{{{{{{\right)

어디^[1]^[5]

$r$ 은 빔의 중심축으로부터의 반경 거리입니다.
$z$ 는 빔의 초점(또는 "축 방향")에서 축 방향 거리입니다.
$i$ 는 상상의 단위이다.
$k$ = $2µn / m2$ 는 자유공간 파장 $θ$ 에 대한 파수(미터당 라디안 단위)이며, n은 빔이 전파되는 매체의 굴절률이다.
$E 0 = E$ ( $0,$ $0$ $),$ 원점( $r$ = 0, z = $0$ ),
$w (z)$ 는 빔을 따라 $평면$ z에서 필드 진폭이 축 값의 1 $/ e$ (즉, 강도 값이 축 값의 1/ $e$ 로² $떨어지는$ 경우)로 $떨어지는$ 반지름이다.
$w 0 = w$ (0 $)$ 는 허리 반지름이다.
$R (z)$ 는 $z$ 에서의 빔 파형의 곡률 반지름입니다.
$γ ($ z)는 빛의 위상 속도에 기인하는 위상 이상의 추가 위상항인 z에서의 Gouy $위상$ 이다.

이러한 단계적 양을 곱하는 이해된 시간 $의존성 iωt$ e도 있다. 시공간에서의 실제 장은 그 복잡한 양의 실제 부분에 의해 주어진다.이 시간 인자는 불투명도에 대한 수학적 설명 complex 복합 켤레 모호성에서 논의된 대로 임의 부호 규칙을 포함한다.

이 솔루션은 근축 근사에 의존하기 때문에 매우 강한 분산 빔에는 정확하지 않습니다. $위$ 의 형식은 대부분의 실제 상황에서 유효합니다. $여기$ 서₀ w ≫/ " / $n$ 。

해당하는 강도(또는 방사선 조도) 분포는 다음과 같다.

{\displaystyle I(r,z)={ E(r,z)^{2} \over 2\eta } =I_{0}\left({\frac {w_{0}}{w(z)}}}\right)^{2}\exp \left({\frac {-2r^{2}}{w(z)^2}}\right}),

여기서 상수 $θ$ 는 빔이 전파되는 매체의 파형 임피던스입니다. $빈$ 공간은 = = 7 $377Ω$ 입니다₀. $I 0 = E 0$ / $2µ$ 는 빔의 허리 중심 강도입니다.

P가 빔의 총출력인 $경우 0$ ,

I_{0}={2P_{0} \over \pi w_{0}^{2}.

진화하는 빔 폭

가우스 함수의

직경

은 1

/ e 2

(텍스트에 사용된 경우

2w

)로 FWHM의 약 1.7배입니다.

빔을 따라 위치 $z$ (초점으로부터 측정)에서 스폿 크기 $파라미터$ w는 쌍곡선으로 ^[1]지정됩니다.

w(z)=w_{0},{\displayrt {1+{\leftfrac\frac {z}{z_{\mathrm {R}}}}\오른쪽}}^{2}}},

어디^[1]

z_{\mathrm {R}}=blac {pi w_{0}^{2}n}{\displayda }

아래에서 자세히 설명하는 것처럼 레일리 범위라고 하며,

\displaystyle

n은

n

매체의 굴절률입니다.

$빔$ 을 따라 임의의 $위치$ z에서 빔 w $(z)$ 의 반지름은 다음에 ^[6]따라 해당 위치의 강도 분포의 절반 최대(FWHM)에서 전폭과 관련됩니다.

w(z)=paramfrac {{\text}FWHM}}(z)}{\sqrt {2\ln2}}}.

파면 곡률

웨이브프론트의 곡률은 허리 양쪽에서 레일리 거리에서 $z$ = ± $z$ 로_R 가장 크며, 허리 자체에서 0을 교차합니다.레일리 거리 $(z R$ > z)를 벗어나면 다시 크기가 감소하여 z $\to$ ± $120$ 으로 0에 근접한다.곡률은 종종 곡률 반지름인 $역수$ R로 표현됩니다. 기본 가우스 빔의 경우 $위치$ z에서의 곡률은 다음과 같이 표시됩니다.

{{displaystyle {1}{R(z)}=squalfrac {z}{z^{2}+z_{\mathrm {R}^{2}}}}

따라서 $곡률$ 반지름 R $(z)$ 은

R(z)=z\left[{1+{\left({\frac {z_{\mathrm {R}}}}}}\right]}^{2}}\right]

곡률의 역수이므로 곡률 반경은 부호를 반전시키고 곡률이 0을 통과하는 빔 웨이스트에서 무한합니다.

구이상

Gouy 위상은 초점 영역 주변의 빔에 의해 점진적으로 획득되는 위상 진행입니다. $위치$ z에서 기본 가우스 빔의 Gouy 위상은 다음과^[1] 같이 주어진다.

\displaystyle \psi (z)=\arctan \leftfrac {z}{z_{\mathrm {R}}\right.}

구이 단계.

Gouy 단계는 허리 부근의 겉보기 파장의 증가를 초래한다( $z 0$ 0).따라서 해당 영역의 위상 속도는 공식적으로 빛의 속도를 초과합니다.이 역설적인 동작은 빛의 위상 속도로부터의 이탈(정확히 평면파에 적용됨)이 매우 작은 근거리 현상으로 이해되어야 한다. 단, 이 경우 파형의 곡률(이전 섹션 참조)은 s의 거리에 걸쳐 상당히 변화한다.잉글 파장모든 경우에 파동 방정식은 모든 위치에서 충족됩니다.

Gouy 단계의 부호는 전기장 ^[7]위상기에 대해 선택된 부호 규칙에 따라 달라집니다.e의존성에서는 $iωt$ $-θ$ / $2$ 에서+ $θ /2$ 로 변화하고 $e의존성$ 에서는^-iωt 축을 $따라$ + $θ/$ $2에서 -θ$ /2로 변화한다.

기본 가우스빔의 경우 허리 한쪽 원필드에서 반대쪽 원필드로 이동함에 따라 Gouy 위상은 $δ라디안$ (즉 위상반전)에 이르는 빛의 속도에 대한 순위상 불일치를 초래한다.이 위상 변동은 대부분의 실험에서 관측할 수 없습니다.그러나 이는 이론적으로 중요하며 고차 가우스 ^[7]모드의 경우 더 큰 범위를 차지합니다.

및 빔

많은 레이저 빔의 단면은 타원형입니다.또한 난시 빔이라고 불리는 두 가로 치수에 대해 다른 허리 위치를 가진 빔도 일반적입니다.이러한 빔은 위의 두 가지 진화 방정식을 사용하여 처리할 수 있지만 x $및$ y에 $대한$ 각 매개 변수의 개별 값과 $z$ = 0 $지점$ 의 개별 정의를 사용합니다.Gouy 위상은 각 치수의 기여도를 합산하여 올바르게 계산된 단일 값이며, 각 치수의 기여도 ± $θ /4$ 범위 내의 Gouy 위상은 각 치수의 기여도입니다.

타원형 빔은 원장에서 허리로 전파될 때 타원비를 반전시킵니다.허리에서 멀리 떨어져 있는 치수는 허리 부근의 치수는 허리 근처가 작아집니다.

가우스 빔의 필드의 기하학적 의존성은 빛의 파장 $δ$ (자유 공간이 아닌 경우 유전 매질 내)와 다음 빔 파라미터에 의해 제어되며, 이 모든 것은 다음 절에서 자세히 설명한 바와 같이 연결됩니다.

쌍곡선을 형성하는

빔

을 따른 거리 z의 함수로서의 가우스 빔 폭

w

(

z)

w 0

: 빔 허리,

b

: 초점 깊이,

z R

: 레일리 범위,

δ

: 총 각도 범위

주어진 $파장$ θ의 가우스 빔의 모양은 빔 $웨이스트 0$ w라는 하나의 파라미터에 의해서만 제어됩니다.이는 빔 폭 $w (z)$ 가 가장 작은 지점(및 마찬가지로 축에서 강도( $r$ = 0)의 초점 지점( $위$ 방정식에서는 z = $0$ )에서 빔 크기를 측정한 것입니다.이 파라미터에서 빔 형상을 설명하는 다른 파라미터가 결정됩니다.여기에는 다음과 같이 Rayleigh $range R$ z 및 점근 빔 발산 $δ$ 가 포함됩니다.

및

레일리 거리 또는 레일리 $범위 R$ z는 가우스 빔의 허리 크기에 따라 결정됩니다.

({=w_{2} {\ ({displaystyle z_{\mathrm {R}} = black {pi {0}^2}n}{\blashda } ） 。}

여기서 $θ$ 는 빛의 파장, $n$ 은 굴절률이다.허리로부터 레일리 $범위 R$ z와 같은 거리에서 빔의 $폭$ w는 빔 허리 w = $w$ 인₀ 초점보다 2 $이상$ 크다.즉, 온축( $r$ = $0$ ) 명암은 피크 명암( $z$ = $0$ )의 절반입니다.빔을 따라 있는 이 점은 파면 $곡률(1$ /R)이 가장 ^[1]큰 지점이기도 합니다.

두 $점$ z = ± $z R$ 사이의 거리를 ^[8]빔의 공초점 매개변수 또는 초점 깊이라고 합니다.

발산

가우스 함수의 꼬리가 실제로 0에 도달한 적은 없지만, 다음 설명의 목적상 빔의 "엣지"는 r $=$ w( $z)$ 인 반지름으로 간주된다.여기서 강도가 온축 값의 1 $/ e$ 로² 떨어졌습니다.이제 z $µz$ 의_R $경우$ $파라미터$ w $(z)$ 가 z와 $선형$ 으로 증가합니다.즉, 허리로부터 멀리 떨어져 있는 빔의 "엣지"가 원뿔 모양임을 의미합니다.해당 원뿔( $표준$ r = $w (z))$ 과 빔 축( $r$ = $0$ ) 사이의 각도는 빔의 분산을 정의합니다.

\displaystyle \theta =\lim _{z\to\infty}\arctan \leftfrac {w(z)}{z}\right.}

근축의 경우, 우리가 고려해온 것처럼, $θ$ (라디안 단위)는 다음과^[1] 같다.

=displaystyle \theta = flac {\pi nw_{0}

$여기$ 서 n은 빔이 전파되는 매질의 굴절률이고 $θ$ 는 자유공간 파장입니다.다음에, 발산 빔의 총 각도 범위 또는 위에서 설명한 원뿔의 정점 각도는 다음과 같이 주어진다.

=displaystyle\Theta=2\Theta)}}}:

그러면 이 원뿔은 가우스 빔의 총 전력의 86%를 포함합니다.

이 확산은 스폿 크기에 반비례하기 때문에 소정의 파장 $θ$ 에 대해 작은 스폿에 초점을 맞춘 가우스 빔은 포커스로부터 멀어짐에 따라 빠르게 확산된다.반대로, 원거리에서의 레이저 빔의 분산을 최소한으로 억제하기 위해서는(또한 원거리에서의 피크 강도를 높이려면) 허리에 큰 단면( $w 0$ $)$ 이 있어야 한다( $w ($ z)는 결코 $w$ 보다₀ 작지 않기 $때문$ 에, 그것이 발사되는 큰 직경이 필요하다.빔 폭과 발산 사이의 이러한 관계는 Fraunhofer 회절을 설명하는 회절 및 푸리에 변환의 기본 특성입니다.지정된 진폭 프로파일을 가진 빔도 이 역관계에 따르지만 기본 가우스 모드는 초점에서의 빔 크기와 원거리장 확산의 곱이 다른 어떤 경우보다 작은 특수한 경우입니다.

가우스 빔 모델은 근축 근사를 사용하기 때문에 ^[9]파형이 빔 축에서 약 30° 이상 기울면 실패합니다.위의 발산 표현식에서는 가우스 빔 모델이 웨이스트가 약 $2µ/ µ$ 보다 큰 빔에 대해서만 정확하다는 것을 의미합니다.

레이저광 품질은 빔 파라미터 제품(BPP)에 의해 정량화된다.가우스 빔의 경우 BPP는 빔의 발산 및 허리 $크기 0$ w의 산물입니다.실제 빔의 BPP는 빔의 최소 직경과 원거리장 차이를 측정하여 산출물을 취함으로써 얻을 수 있습니다.같은 파장에서 이상적인 가우스 빔의 BPP에 대한 실제 빔의 BPP의 비율을 M("M 제곱")이라고 $합니다 2$ .가우스 빔의 $M$ 은² 1입니다.모든 실제 레이저 $빔$ 은² M 값이 1보다 크지만 매우 고품질 빔은 1에 매우 가까운 값을 가질 수 있습니다.

가우스 빔의 수치 개구부는 NA = $n$ sin $δ$ 로 정의되며, $여기$ 서 n은 빔이 전파되는 매체의 굴절률이다.이것은 레일리 범위가 다음과 같이 숫자 구멍과 관련이 있다는 것을 의미합니다.

}{\displaystyle z_{\mathrm {R}}=snfrac {nw_{0}}{\mathrm {NA}}}.}

와 강도

전원 공급

빔이 조리개를 중심으로 위치 $z$ 에서^[10] 가로 평면에서 $반지름$ r의 원을 통과하는 힘 $P$ 는 다음과 같습니다.

Pdisplaystyle P(r,z)=P_{0}\left [1-e^{-2r^{2}/w^{2}(z)}\right],}

서 ''는

frac I_displaystyle P_{0}=pi frac {1}{2}\pi I_{0}w_{0}^2}

빔에 의해 전달되는 총 전력입니다.

$반지름$ r = $w (z)$ 인 원의 경우, 원을 통해 전달되는 힘의 비율은 다음과 같다.

{P0.865). (\displaystyle\frac{P(z)}{P_{0}=1-e^{-2}\ 0.865).}

마찬가지로 빔 동력의 약 90%는 $반지름$ r $=$ $1.07$ × $w (z)$ 의 원을, 95%는 $반지름 r = 1$ . $224$ × w(z)의 원을, $99%는 반지름$ r $=$ ^[10] 1.52 × w $(z$ )의 원을 통해 흐릅니다.

강도(Peak Intensity)

빔 웨이스트에서 축 $거리$ z에서의 피크 강도는 $반지름$ r의 원 내에서 둘러싸인 힘의 한계로 계산할 수 있습니다. 원은 축소될 때 원 $µr$ 의² 면적으로 나눕니다.

I(0,z)=\lim _{r\to 0}{\frac {P_{0}\left [1-e^{-2r^{2}/w^{2}(z)\right]{\pi r^{2}}}}.

한계는 L'Hopital의 법칙을 사용하여 평가할 수 있습니다.

}{\displaystyle I(0,z)=pic frac {P_{0}{\pi}\lim _{r\to 0}{\frac {-(-2)(2r)e^{-2r^{2}/w^{2}(z)\right}{w^{2}(z}}{w^{w^{w}(z}{r}}}{r}}}}{r}}}}{pi}{r}{r}}}{r}}}{pi}}{pi}}}}}{pic fr}

빔을 따라 $z$ 의 함수로서 가우스 빔의 스폿 크기와 곡률도 다음과 같이 복잡한 빔 $파라미터$ q( $z)$ ^[11]^[12]로 인코딩할 수 있습니다.

}{\displaystyle q(z)=z+iz_{\mathrm {R}}}

이 복잡성을 도입하면 다음과 같이 가우스 빔 필드 방정식이 단순화됩니다.q $(z)$ 의 역수는 각각 ^[11]실제 부분과 가상의 부분에 파면 곡률 및 상대 축 위 강도를 포함하고 있음을 알 수 있다.

}{\displaystyle {1 \over q(z)}={1 \over z+iz_{\mathrm {R}={z \over z^{2}+z {R}} {\mathrm {R}} } \over z^{2}+z_{\mathrm {R}} ={1} ={1} {1}

복잡한 빔 매개 변수는 가우스 빔 전파의 수학적 분석, 특히 광선 전달 행렬을 사용한 광학 공진기 공동 분석을 단순화합니다.

그런 다음 이 형식을 사용하여 전기(또는 자기)장에 대한 이전의 방정식을 크게 단순화할 수 있습니다.u를 $타원형$ 가우스 빔의 상대 전계 강도(x 및 $y$ 방향의 타원 축)라고 $부르면$ 다음과 같이 x $및$ $y$ 로 분리할 수 있습니다.

udisplaystyle u(x,y,z)=u_{x}(y,z)}}

서 ''는

{\displaystyle{\begin{정렬}(x,z)&, =ᆲᆳ_ᆴ(z)}}}\exp \left(-ik{\frac{{2}}{2{q}_{x}(zx^)}}\right),\\u_ᆵ(y,z)&, =ᆶᆷ_ᆸ(z)}}}\exp \left(-ik{\frac{{2}}{2{q}_{y}(zy^)}}\right),\end{정렬}}}{\displaystyle{\displayrt{q}(z)}\displaystyle{\displayfrac{\displaystyle{\displayrt{q}(z)\exp.}}}\right,\u_{y}(z)&=frac1}{displaysty}{1}

$여기$ 서_xq( $z)$ $및 y$ q( $z)$ 는 $x$ $및$ y 방향의 복잡한 빔 파라미터입니다.

원형 빔 프로파일의 일반적인 경우 $q y$ ( $z) = q$ ( $z) =$ q( $z)$ $및 2$ x + $y 2$ = $r$ 은² $다음$ 과_x^[13] 같습니다.

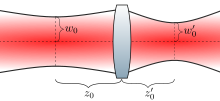
({displaystyle u(r,z)=syslogfrac {1}{q(z)}\exp \left \syslogik frac {r^{2}}{2q(z)}}\right).}

렌즈를 통과하는 가우스 빔의 다이어그램.

가우스 빔이 얇은 렌즈를 통해 전파될 때 빔이 렌즈의 원통 대칭 축을 따라 이동한다는 전제 하에 나가는 빔도 (다른) 가우스 빔입니다. $렌즈$ f $(\displaystyle$ f $f$ 빔 허리 $w_{0}$ $(\$ 및 빔 허리 $z_{0}$ z $(\$ 의 $z_{0}$ 초점 거리를 $w_{0}'$ 하여 빔 허리 반경 $(\$ 와 $w_{0}'$ z $(\$ 의 $z_{0}'$ 위치를 결정할 수 있습니다.나가는 빔

Saleh와 Teich에 의해 도출된 것처럼,^[14] 잉고 빔과 발신 빔의 관계는 렌즈를 통과할 때 가우스 빔의 각 점 $(x,y)$ $y)$ 에 추가되는 위상(x, y $)$ 을 $(x,y)$ 고려하여 확인할 수 있습니다.Self에 의한 다른 접근법은 가우스 빔 ^[15]파동에 대한 얇은 렌즈의 영향을 고려하는 것입니다.

위의 문제에 대한 정확한 해결책은 간단히 $배율$ M $(\displaystyle$ M $)$ 로 표현됩니다.

{begin{0}w_{0}'&=Mw_{0}\[1.2ex](z_{0}-f)&=M^{2}(z_{0}-f)end {aligned

$w_{0}$ 0 $(\$ 및 $z_{0}$ $(\$ 에 $w_{0}$ 달라지는 배율은 다음과 같습니다.

{\ M2displaystyle M=mbrc {M_{r}}{\sqrt {1+r^{2

서 ''는

}{\displaystyle r=frac {z_{R}-f},\quad M_{r}=\left {f}{z_{0}-f}}\right .}

빔 $z_{0}'$ $z_{0}'$ 0 $z_{0}'$ {\(\ $displaystyle z_{0}')$ 에 $z_{0}'$ 대한 등가 표현식은 다음과 같습니다.

{{displaystyle {1}{z_{0}+{\frac {z_{R}^2}}}{(z_{0}-f)}}}}}}}}}+{\frac {1}=frac {1}{f}}}.}

이 마지막 표현은 (z $\left|\left({\tfrac {z_{R}}{z_{0}}}\right)\left({\tfrac {z_{R}}{z_{0}-f}}\right)\right|\ll 1$ z $\left|\left({\tfrac {z_{R}}{z_{0}}}\right)\left({\tfrac {z_{R}}{z_{0}-f}}\right)\right|\ll 1$ $\left|\left({\tfrac {z_{R}}{z_{0}}}\right)\left({\tfrac {z_{R}}{z_{0}-f}}\right)\right|\ll 1$ R $\left|\left({\tfrac {z_{R}}{z_{0}}}\right)\left({\tfrac {z_{R}}{z_{0}-f}}\right)\right|\ll 1$ - $\left|\left({\tfrac {z_{R}}{z_{0}}}\right)\left({\tfrac {z_{R}}{z_{0}-f}}\right)\right|\ll 1$ ) ${\$ $\left|\left({\tfrac {z_{R}}{z_{0}}}\right)\left({\tfrac {z_{R}}{z_{0}-f}}\right)\right|\ll 1$ ({\ $tfrac {z_{R}}{z_{0}}\right)\left$ ({\ $tfrac {z_{R}}{z_{0$ }}}\ $right$ })\left $({\tfrac$ {z_{0 $}\$ right})\llllll}\ $right)$ 라는 한계 내에서 광섬유 박렌즈 방정식이 복구됨을 나타냅니다 $\left|\left({\tfrac {z_{R}}{z_{0}}}\right)\left({\tfrac {z_{R}}{z_{0}-f}}\right)\right|\ll 1$ $\left|z_{0}+{\frac {z_{R}^{2}}{z_{0}-f}}\right|\gg f$ $\left|z_{0}+{\frac {z_{R}^{2}}{z_{0}-f}}\right|\gg f$ 0 $\left|z_{0}+{\frac {z_{R}^{2}}{z_{0}-f}}\right|\gg f$ - $\left|z_{0}+{\frac {z_{R}^{2}}{z_{0}-f}}\right|\gg f$ {\ $displaystyle \left z_{0}+{\frac {z_{R}^{2}}-f}\right \gg$ f}는 $\left|z_{0}+{\frac {z_{R}^{2}}{z_{0}-f}}\right|\gg f$ 입사빔을 "잘 콜리메이트"하여 z $z_{0}'\approx f$ f {\ $display z_{0}\about$ f $z_{0}'\approx f$ 가 되도록 $z_{0}'\approx f$ .

★★★★★

일부 용도에서는 수렴 렌즈를 사용하여 레이저 빔의 초점을 매우 작은 지점에 맞추는 것이 바람직합니다.수학적으로 이는 $배율$ M $({displaystyle$ M $M$ 의 최소화를 의미합니다.빔의 크기가 사용 가능한 광학의 크기에 의해 제한되는 경우 일반적으로 가능한 한 큰 콜리메이트된 빔을 작은 초점거리 렌즈를 통해 전송하여 $({$ })를 $z_{R}$ $z_{R}$ 하고 최소화하는 것이 가장 좋습니다. $f$ {\ $displaystyle$ f $f$ 이 상황에서는 $z_{R}^{2}/(z_{0}-f)^{2}\gg 1$ $z_{R}^{2}/(z_{0}-f)^{2}\gg 1$ $z_{R}^{2}/(z_{0}-f)^{2}\gg 1$ 2 / ( $z_{R}^{2}/(z_{0}-f)^{2}\gg 1$ 0 $z_{R}^{2}/(z_{0}-f)^{2}\gg 1$ - $z_{R}^{2}/(z_{0}-f)^{2}\gg 1$ ) ${\$ 1 {{ $displaystyle z_{R}^{2}/(z_{0}-f)^{g$ 1)로 $z_{R}^{2}/(z_{0}-f)^{2}\gg 1$ 하여 M $M\approx f/z_{R}$ / Z $M\approx f/z_{R}$ {\ $displaystyle$ M $\approxf/z}$ 의 $M\approx f/z_{R}$ 결과를 얻을 수 있습니다 $.$ $x fw_{0}/z_{R$ 이 결과는 종종 다음 형식으로 나타납니다.

{ { } _ { } & \ \ { \ F _ { \ # } \ \ .2ex ]_ { } \ displaystyle \ } 2w _ 0 } & \ frac { } \ pi }

서 ''는

{displaystyle F_{\#}=flac {f}{2w_{0}})

이 값은 $n\approx 1$ 의 굴절률이 1 $({displaystyle$ n $\$ $approx$ $n\approx 1$ 1)이라고 $n\approx 1$ 가정하고 $z_{R}=\pi w_{0}^{2}/\lambda$ R $=$ $z_{R}=\pi w_{0}^{2}/\lambda$ w 0 2 / $dis$ { $display z_$ {R}=\ $pi$ w_ ${0$ }^ $2$ $/\$ lamda $z_{R}=\pi w_{0}^{2}/\lambda$ 이며, 빔 크기를 허리 $2w_{0}'$ $2w_{0}'$ 으로 표시하는 것을 공통적으로 선호하기 때문에 2 인수가 도입되었다 $2w_{0}'$ $playstyle 2w_{0}'}$ and $2w_{0}$ , rather than the waist radii $w_{0}'$ and $w_{0}$ .

전자기 방사선의 특수한 경우로서 가우스 빔(및 아래에 자세히 설명되어 있는 고차 가우스 모드)은 자유 공간 또는 균질 유전 ^[16]매체의 전자장에 대한 파동 방정식에 대한 해로, $E$ 의 컬과 $H$ 의 컬에 대한 Maxwell의 방정식을 결합하여 다음과 같은 결과를 얻을 수 있습니다.

\displaystyle ^{22}U = flac {1} {c^{2}} {\frac ^{2}} tU}{\partial t^{2}},}

여기

서 c는 매질에서 빛의

속도

이며, U는 전기장 또는 자기장 벡터를 참조할 수 있습니다. 이는 어느 하나의 특정 솔루션이 다른 것을 결정함에 따라 결정됩니다.가우스 빔 솔루션은 근축 근사, 즉 파동 전파가 축의 작은 각도 내의 방향으로 제한되는 경우에만 유효합니다.일반성을 잃지 않고, 이 경우

솔루션

U는 일반적으로 시간에 의존하지 않고 비교적 부드럽게 공간적으로 변화하는 u로

기술

할 수 있으며,

주요

변동은

z

^[16]방향의 파장에 공간적으로 대응한다.

\displaystyle U(x,y,z,t)=u(x,y,z)e^{-i(kz-\Omega t),{\hat {mathbf {x}}}}}

근축근사와 함께 이 형태를 사용하면 $2 u / θz$ 를² 근본적으로 무시할 수 있다.전자파 방정식의 해는 전파 방향( $z$ )과 직교하는 편광에 대해서만 유지되므로 일반성의 손실 없이 편광을 x $방향$ 으로 간주하여 이제 u $(x,$ $y,$ $z)$ 에 $대한$ 스칼라 방정식을 풀 수 있습니다.

위의 파동 방정식에 이 솔루션을 대입하면 스칼라 파동 ^[16]방정식에 대한 근축 근사치가 산출됩니다.

{\frac x^{2}}+{\frac y^{2}=2ikfrac {\frac z}.

광원추 좌표에 파동 방정식을 작성하면 근사치를^{[citation needed]} 사용하지 않고 이 방정식이 반환됩니다.임의의 빔

웨이스트 0

w의 가우스빔은 스칼라파 방정식에 대한 근축근사를 만족한다.이것은 위에서 정의한 복소빔

파라미터

q(

z)

로 z에서의

파형

을 표현함으로써 가장 쉽게 검증된다.그 밖에도 많은 해결책이 있습니다.선형 시스템에 대한 솔루션으로서, 어떤 솔루션 조합(더하기 또는 상수 곱셈 사용)도 해결책이 됩니다.기본 가우스란 위에서 설명한 바와 같이 최소 스폿 크기와 원거리장 확산의 곱을 최소화하는 것이다.근축 해법, 특히 기본 가우스 모드가 아닌 레이저 방사선을 설명하는 해법에서는 분기와 최소 스폿 크기의 곱이 점차 증가하는 해법 패밀리를 찾는다.이러한 종류의 두 가지 중요한 직교 분해는 다음 절에서 상술한 바와 같이 각각 직사각형 대칭과 원형 대칭에 대응하는 에르미트-가우스 모드 또는 라게르-가우스 모드이다.둘 다 기본 가우스 빔이 가장 낮은 차수 모드입니다.

고차 모드

Hermite-Gaussian 모드

12개의 에르미트-가우스 모드

이른바 에르미트-가우스 모드의 직교 세트를 사용하여 간섭성 근축 빔을 분해할 수 있습니다. 이 모드는 $x$ 의 인자와 $y$ 의 인자의 곱에 의해 제공됩니다.이러한 해는 데카르트 ^[17]좌표로 기술된 근축 헬름홀츠 방정식의 $x$ 와 $y$ 의 분리성 때문에 가능하다. $따라서$ x, $y$ 방향을 참조하는 순서 모드( $l,$ $m)$ 가 주어지면 x, $y,$ $z$ 에서의 전계 진폭은 다음과 같이 구할 수 있습니다.

\displaystyle E(x,y,z)=u_{l}(x,z),u_{m}(y,z),\exp(-ikz),}

여기

서 x 및

y

종속성에 대한 요인은 각각 다음과 같습니다.

{\displaystyle u_{J}(x,z)=\left({\frac {2/\pi }}{2^{J},\;w_{0}}\right)^{\!\!1/2}\!!\leftfrac\frac{q}_{0}{q}(z)}}}\right)^{\!\!1/2}\!!\!\left {\frac {{q}^{\ast }(z)}{{q}(z)}}}\right)^{\!J/2}\!H_{J}\!\left({\frac {\sqrt {2}}x}{w(z)}}}\right),\exp \left(\!-i{kx^{2}}{2{q}(z)}}}\right},

여기서는 포커스에서

z

에 있는

허리 0

빔에 대해 복잡한 빔

매개변수 q (

z)를 사용했다.이 형태에서 첫 번째 인자는 정규화 상수일 뿐이며, 정규화

J

집합을 만듭니다.두 번째 요인은 z에

의존

하는 추가 정규화이며, w

(z

)/

w 0

(마지막 두 가지 요인 때문에)에 따라 모드의 공간 범위 확장을 보상합니다.또한 Gouy 단계의 일부도 포함되어 있습니다.세 번째 요인은 고차

J

에 대한 Gouy 위상 이동을 향상시키는 순수 위상입니다.

마지막 두 요인은 x( $또는$ y)에 대한 공간 변동을 설명합니다.네 번째 인자는 J $차수$ 의 에르미트 다항식("즉, $H 1 (x)$ = $2x$ ")이고, 다섯 번째 인자는 가우스 진폭 하락 $expµx 2 / w (z) 2$ 를 설명하지만, 이는 지수의 $복소수$ q를 사용하면 명백하지 않다.또한 이 지수를 확장하면 빔을 따라 $z$ 에서 파면 $곡률(1 / R ($ z))을 설명하는 x의 $위상$ 계수가 생성됩니다.

Hermite-Gaussi 모드는 일반적으로 "TEM_lm"으로 지정됩니다. 따라서 기본 가우스 빔은 TEM(여기서 TEM은 횡단 전자파)이라고₀₀ 불립니다.u $(x,$ $z)$ 와_mu( $y, z$ )를 $곱하여 l$ 2-D 모드프로파일을 취득하고 정규화를 삭제하여 선행 계수가 E로 $호출$ 되도록₀ 하면 $접근$ 하기쉬운 $형태$ 로 (l, m $)$ 모드를 쓸 수 있습니다.

aligned {E_{l,m}(x,y,z)={}&E_{0}{\frac {w_{0}}{w(z)}}}}}, H_{l}\!frac {\sqrt {2}},x}{w(z)}}{\Bigg},H_{m}\!{\}} {2z)}}}{\times \leftfrac y^{2Bigg(}}{\frac {\sqrt {2}},y(z}}}}}}}}}}}}\t {\times}}{w^{2}(z)}}}\right)\exp \leftfrac {k(x^{2}+y^{2}}}}}\right)\exp {}\&\exp {}(i\psi(z){\big}\ex}\exp(ikz).end {aligned}

이 형태에서 $매개변수 0$ w는 이전과 같이 모드 패밀리, 특히 z = $0$ 에서 $기본$ 모드의 허리와 다른 모든 모드 패턴의 공간 범위를 스케일링합니다. w, $w (z)$ 및 $R (z)$ 는 $위$ 에서₀ 설명한 기본 가우스 빔에 대해 동일한 정의를 가집니다.l = $m$ = $0일$ 때 앞에서 설명한 기본 가우스 빔을 얻을 수 있습니다(H = $1$ $이후 0$ ). $임의$ 의 z에서 x $프로파일$ 과 y 프로파일의 유일한 특정한 차이는 $순서$ 번호 $l$ 과 m에 대한 에르미트 다항식 요인 때문입니다.그러나 z에 $대한$ 모드의 Gouy 단계의 진화에 변화가 있습니다.

z}{z_{Rdisplaystyle \psi(z)=(N+1),\arctan \leftfac {z}{\mathright},\right})

여기서 $모드$ N의 결합 순서는 N $= l$ + $m$ 으로 정의된다.기본(0,0) 가우스 모드의 Gouy 위상 편이는 $모든$ z에 $대해$ ± $µ/$ 2 라디안만 변경되지만( $및 R$ ±z $사이$ 의± $µ$ /4 라디안만 변경), 고차 ^[7]모드의 경우 N + $1$ $계수$ 만큼 증가합니다.

에르미트 가우스 모드는 직사각형 대칭을 가지며, 공동 설계가 직사각형 방식으로 비대칭인 레이저에서 나오는 방사선의 모달 분석에 특히 적합합니다.한편, 레이저나 원형 대칭의 시스템은, 다음의 항에서 설명하는 Laguerre-Gauss 모드 세트를 사용해 보다 효율적으로 취급할 수 있습니다.

Laguerre-Gaush 모드

원형 대칭인 빔 프로파일(또는 원통 대칭인 공동이 있는 레이저)은 종종 라게르-가우스 모달 ^[3]분해를 사용하여 가장 잘 해결됩니다.이러한 함수는 일반화된 Laguerre 다항식을 사용하여 원통형 좌표로 작성됩니다.각 횡단 모드는 두 개의 정수를 사용하여 다시 라벨링된다. 이 경우 반경 $지수$ p ≤ $0$ 과 양수 또는 음수(또는 0)^[18]가 될 수 있는 방위 $지수$ l:

l=1 및 p=0인 Laguerre-Gaussian 빔

{\displaystyle {aligned}u(r,\phi,z)={}&C_{lp}^{LG}{\frac {w_{0}{w(z)}}\left({\frac {r{\sqrt {2}}}{w(z}}}}}\right)^{\! l }\exp \!\left(\frac {r^{2}}{w(z}}}}}}\right)L_{p}^{ l }\!\left({\frac {2r^{2}}{w^{2}(z)}}\right)\times {}\&\exp \!\left(\!-ik{\frac {r^{2}}}{2R(z)}}}}\exp(-il\phi(z)\end}}}},\exp(i\exp(i\right)

$여기$ 서_p^l L은 일반화 라게르 다항식이다. $C$ 는^LG
_lp 필수 정규화 상수입니다.

C_{lp}^{LG={frac{2p!}{\pi(p+l )!}}\오른쪽 화살표 \int _{0}^{2\pi }d\phi \int _{0}^{\infty }rdr u(r,\phi,z)^{2}=1

.

$w (z)$ $및$ R $(z)$ 의 정의는 위와 같습니다.고차 헤르미트-가우스 모드와 마찬가지로 라게르-가우스 모드의 구이 위상 편이는 N + $1$ $계수로$ 과장됩니다.

(\displaystyle \psi(z)=(N+1),\arctan \leftfac {z}{\mathrm {R}}\right),}

이 경우 결합

모드

번호

N

= l +

2p

입니다.이전과 마찬가지로 가로 진폭 변동은 방정식의 위쪽 라인에 있는 마지막 두 요인에 포함됩니다. 이 요인에는 기본 가우스 드롭오프(r)가 포함되지만 이제 라게르 다항식이 곱됩니다.회전 모드

번호

l의 효과는 Laguere 다항식에 영향을 미칠 뿐만 아니라 주로 위상

계수

exp

(- il),)

에 포함됩니다. 위상 계수 exp(-il),)에서는 빔 프로파일이 빔을 중심으로 1회전(

φ

)으로

2µ

위상이

완료

됩니다.이것은 위상

전하

l의 광학적 소용돌이의 한 예이며, 이 모드에서 빛의 궤도 각운동량과 연관될 수 있다.

Ince-Gaush 모드

광섬유의 ^[19]출력으로 기록된 Ince-Gaussian 모드의 시뮬레이션 프로파일(상부) 및 대응하는 사진(하부)

타원 좌표에서는 Ince 다항식을 사용하여 고차 모드를 작성할 수 있습니다.짝수 및 홀수 Ince-Gaussi 모드는 다음과^[20] 같습니다.

{\displaystyle u_{\varepsilon }\left(\xi,\eta,z\right)=sq {w_{0}{w\left(z\right)}}\mathrm {C}_{p}{m}\left(i,\xi,\varepsilon\right)_{c}\arepsilon}\eta,\left(왼쪽)

여기서

θ

와

θ

는 다음과 같이 정의된 반지름 및 각도 타원 좌표입니다.

(\displaystyle {arepsilon /2}}x&=cosh \xi \cos \eta,\y&=cosh \cos \cos \eta,\xi \sin \sin \eta .\end {aligned})

C m p (θ, θ

)는

p차수

와

m차수

의 짝수 Ince 다항식이다. 여기서

θ

는 타원 파라미터이다.Hermite-Gaussi 모드와 Laguerre-Gaussi 모드는 각각 ^[20]

ε

=

and

respect respect respect

=0

에 대한 Ince-Gaussi 모드의 특수한 경우입니다.

하이퍼 지오메트릭-가우스 모드

원통형 좌표에는 복잡한 진폭이 합류 초기하 함수에 비례하는 또 다른 중요한 근축파 모드의 클래스가 있다.

이러한 모드는 단일 위상 프로파일을 가지며 광자 궤도 각운동량의 고유 함수입니다.명암 프로파일은 1개의 선명한 링으로 특징지어집니다.Laguerre-Gauss 모드와 마찬가지로 명암 프로파일은 기본(0,0) 모드를 제외하고 중심(광축)에서 0으로 떨어집니다.모드의 복합 진폭은 다음과 ^[21]같이 정규화된(무제한) 반경 좌표 $θ$ = $r / w 0$ 및 정규화된 세로 좌표 $δ$ = $z / z$ 의_R 관점에서 쓸 수 있습니다.

{\displaystyle{\begin{정렬}u_{{\mathsf{p}}m}(\rho,\phi ,\mathrm{Z}){}={}&,{\sqrt{\frac{2^{{\mathsf{p}}+m+1}}{\pi \Gamma({\mathsf{p}}+m+1)}}}\;{\frac{\Gamma)}{\Gamma(m+1)}}\,i^{m+1}\times{}\\&,\mathrm{Z}^{\frac{\mathsf{p}}{2}}\,(\mathrm{Z}+i)^{-\left({\frac{\mathsf{p}}{.2}}+m+1\right)},\rho ^{m}\times {}\&\exp \left(-{\frac {i\rho ^{2}}{\mathrm {Z} +i}}\right}, e^{im\phi},{1}F_{1}\left(-{\frac {\rh}) {p} {p}}}, m}, {p}, {\frac {f}, {\rh}, {\rac {\rh}, {\rh}, {\rh},

여기서 $회전지수$ m은 ${\mathsf {p}}\geq -|m|$ 이고 p ${\mathsf {p}}\geq -|m|$ δ - ${\mathsf {p}}\geq -|m|$ { $displaystyle {p}}\geq$ - ${\mathsf {p}}\geq -|m|$ m $}$ 은 ${\mathsf {p}}\geq -|m|$ 실수치이고 $δ(x)$ 는 감마 함수, $F 1 (a,$ $b; x$ )는 합류초기하 함수이다.

하이퍼 지오메트릭 가우스(HyGG) 모드의 일부 하위 패밀리는 수정된 베셀 가우스 모드, 수정된 지수 가우스 ^[22]모드 및 수정된 라게르-가우스 모드로 나열될 수 있다.

하이퍼 지오메트릭-가우스 모드 세트가 너무 완전하며 직교 모드 세트가 아닙니다.복잡한 필드 프로파일에도 불구하고 HyGG 모드의 빔 웨이스트( $z$ = 0)는 매우 단순합니다.

u(\rho,\phi,0)\propto \rho ^{\mathsf {p}+m}e^{-\rho ^{2}+im\phi }}

「」를 참조해 주세요.

메모들

^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ 스벨토, 페이지 153-5.
^ 지그만, 642페이지
^ ^a ^b 아마도 구바우와 슈링(1961년)에 의해 처음 고려되었을 것이다.
^ 스벨토, 페이지 158
^ Yariv, Amnon; Yeh, Albert Pochi (2003). Optical Waves in Crystals: Propagation and Control of Laser Radiation. J. Wiley & Sons. ISBN 0-471-43081-1. OCLC 492184223.
^ Hill, Dan (April 4, 2007). "How to Convert FWHM Measurements to 1/e-Squared Halfwidths". Radiant Zemax Knowledge Base. Retrieved June 7, 2016.
^ ^a ^b ^c Paschotta, Rüdiger. "Gouy Phase Shift". Encyclopedia of Laser Physics and Technology. RP Photonics. Retrieved May 2, 2014.
^ Brorson, S.D. (1988). "What is the confocal parameter?". IEEE Journal of Quantum Electronics. 24 (3): 512–515. doi:10.1109/3.155.
^ 시그만(1986) 페이지 630
^ ^a ^b 멜레스 그리오가우스 빔 광학
^ ^a ^b 시그만, 페이지 638-40.
^ Garg, 페이지 165-168.
^ Siegman(1986) 페이지 639 참조. Eq. 29
^ Saleh, Bahaa E. A.; Teich, Malvin Carl (1991). Fundamentals of Photonics. New York: John Wiley & Sons. ISBN 0-471-83965-5. 제3장 "빔 광학"
^ Self, Sidney (1 March 1983). "Focusing of spherical Gaussian beams". Applied Optics. 22 (5): 658–661. doi:10.1364/AO.22.000658.
^ ^a ^b ^c 스벨토, 페이지 148-9.
^ 시그만(1986), 페이지 645, eq. 54
^ Allen, L. (June 1, 1992). "Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes" (PDF). Physical Review A. 45 (11): 8185–8189. Bibcode:1992PhRvA..45.8185A. doi:10.1103/physreva.45.8185. PMID 9906912.
^ Sakpal et al. (2018년)
^ ^a ^b 반드레스와 구티에레즈베가(2004)
^ 카리미 외(2007)
^ 카리미 외(2007)

참조

Bandres, Miguel A.; Gutierrez-Vega, Julio C. (2004). "Ince Gaussian beams". Opt. Lett. OSA. 29 (2): 144–146. Bibcode:2004OptL...29..144B. doi:10.1364/OL.29.000144. PMID 14743992.
Garg, Anupam (2012). Classical Electromagnetism in a Nutshell. Princeton, N.J.: Princeton University Press. ISBN 978-0691130187.
Goubau, G.; Schwering, F. (1961). "On the guided propagation of electromagnetic wave beams". IRE Trans. 9 (3): 248–256. Bibcode:1961ITAP....9..248G. doi:10.1109/TAP.1961.1144999. MR 0134166.
Karimi, E.; Zito, G.; Piccirillo, B.; Marrucci, L.; Santamato, E. (2007). "Hypergeometric-Gaussian beams". Opt. Lett. OSA. 32 (21): 3053–3055. arXiv:0712.0782. Bibcode:2007OptL...32.3053K. doi:10.1364/OL.32.003053. PMID 17975594.
Mandel, Leonard; Wolf, Emil (1995). Optical Coherence and Quantum Optics. Cambridge: Cambridge University Press. ISBN 0-521-41711-2. 5장 "광학 빔", 267페이지.
Pampaloni, F.; Enderlein, J. (2004). "Gaussian, Hermite-Gaussian, and Laguerre-Gaussian beams: A primer". arXiv:physics/0410021.
Sakpal, S.; Milione, G.; Li, M.; Nouri, M.; Shahoei, H.; LaFave, T.; Ashrafi, S.; MacFarlane, D. (2018). "Stability of Ince-Gaussian beams in elliptical core few-mode fibers". Opt. Lett. 43: 2656–2659. doi:10.1364/OL.43.002656.
Saleh, Bahaa E. A.; Teich, Malvin Carl (1991). Fundamentals of Photonics. New York: John Wiley & Sons. ISBN 0-471-83965-5. 3장 "빔 광학", 페이지 80–107.
Siegman, Anthony E. (1986). Lasers. University Science Books. ISBN 0-935702-11-3. 16장
Svelto, Orazio (2010). Principles of Lasers (5th ed.).
Yariv, Amnon (1989). Quantum Electronics (3rd ed.). Wiley. ISBN 0-471-60997-8.

외부 링크

가우스 빔 광학 자습서, 새 포트

[svelto153-1] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ 스벨토, 페이지 153-5.

[siegman642-2] 지그만, 642페이지

[goubau-3] 아마도 구바우와 슈링(1961년)에 의해 처음 고려되었을 것이다.

[svelto158-4] 스벨토, 페이지 158

[5] Yariv, Amnon; Yeh, Albert Pochi (2003). Optical Waves in Crystals: Propagation and Control of Laser Radiation. J. Wiley & Sons. ISBN 0-471-43081-1. OCLC 492184223.

[zemax-6] Hill, Dan (April 4, 2007). "How to Convert FWHM Measurements to 1/e-Squared Halfwidths". Radiant Zemax Knowledge Base. Retrieved June 7, 2016.

[gouy_phase_shift-7] Paschotta, Rüdiger. "Gouy Phase Shift". Encyclopedia of Laser Physics and Technology. RP Photonics. Retrieved May 2, 2014.

[8] Brorson, S.D. (1988). "What is the confocal parameter?". IEEE Journal of Quantum Electronics. 24 (3): 512–515. doi:10.1109/3.155.

[9] 시그만(1986) 페이지 630

[melles_griot-10] 멜레스 그리오가우스 빔 광학

[siegman638-11] 시그만, 페이지 638-40.

[garg168-12] Garg, 페이지 165-168.

[13] Siegman(1986) 페이지 639 참조. Eq. 29

[fourier_derivation_of_gaussian_lens-14] Saleh, Bahaa E. A.; Teich, Malvin Carl (1991). Fundamentals of Photonics. New York: John Wiley & Sons. ISBN 0-471-83965-5. 제3장 "빔 광학"

[wavefront_derivation_of_gaussian_lens-15] Self, Sidney (1 March 1983). "Focusing of spherical Gaussian beams". Applied Optics. 22 (5): 658–661. doi:10.1364/AO.22.000658.

[svelto148-16] 스벨토, 페이지 148-9.

[17] 시그만(1986), 페이지 645, eq. 54

[orbital_momentum_of_light-18] Allen, L. (June 1, 1992). "Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes" (PDF). Physical Review A. 45 (11): 8185–8189. Bibcode:1992PhRvA..45.8185A. doi:10.1103/physreva.45.8185. PMID 9906912.

[ince-gaussian-stability-19] Sakpal et al. (2018년)

[ince-beams-20] 반드레스와 구티에레즈베가(2004)

[21] 카리미 외(2007)

[22] 카리미 외(2007)

[1]

[2]

[3]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

v t 레이저
레이저 기사 목록 레이저 타입 리스트 레이저 응용 프로그램 목록 레이저 줄임말
레이저의 종류	이산화탄소 레이저 화학 레이저 색소 레이저 Er: YAG 레이저 엑시머 레이저 자유 전자 레이저 헬륨 네온 레이저 이온 레이저 레이저 다이오드 액정 레이저 Nd: YAG 레이저 질소 레이저 라만 레이저 Ti-sapshire 레이저 X선 레이저
레이저 물리학	활성 레이저 매체 증폭된 자연 방출 연속파 도플러 냉각 레이저 절제 레이저 냉각 레이저 선폭 레이싱 임계값 자기 광학 트랩 광학 핀셋 모집단 반전 해결된 사이드밴드 냉각 초단파 펄스
레이저 광학	비임 익스팬더 빔 균질화기 B 적분 차프 펄스 증폭 게인 스위칭 가우스 빔 주입식 시드러 레이저광 프로파일러 M 제곱 모드 잠금 다중 프리즘 그레이팅 레이저 발진기 멀티호톤 펄스 내 간섭 페이즈 스캔 광증폭기 광학 공동 광 아이솔레이터 출력 커플러 Q 스위칭 라만 증폭 회생 증폭
카테고리

Search

가우스 빔

네임스페이스

더

목차

수학적 형식

진화하는 빔 폭

파면 곡률

구이상

및 빔

및

발산

와 강도

전원 공급

강도(Peak Intensity)

★★★★★

고차 모드

Hermite-Gaussian 모드

Laguerre-Gaush 모드

Ince-Gaush 모드

하이퍼 지오메트릭-가우스 모드

「」를 참조해 주세요.

메모들

참조

외부 링크

Search

가우스 빔

수학적 형식

진화하는 빔 폭

파면 곡률

구이상

및 빔

및

발산

와 강도

전원 공급

강도(Peak Intensity)

★★★★★

고차 모드

Hermite-Gaussian 모드

Laguerre-Gaush 모드

Ince-Gaush 모드

하이퍼 지오메트릭-가우스 모드

「 」를 참조해 주세요.

메모들

참조

외부 링크

「」를 참조해 주세요.