순서-7-3 삼각 벌집
Order-7-3 triangular honeycomb| 순서-7-3 삼각 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {3,7,3} |
| 콕시터 도표 | |
| 세포 | {3,7} |
| 얼굴 | {3} |
| 에지 피겨 | {3} |
| 정점수 | {7,3}  |
| 이중 | 셀프듀얼 |
| 콕시터군 | [3,7,3] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서 7-3 삼각형 벌집(또는 3,7,3 벌집)은 슐래플리 기호 {3,7,3}이(가) 있는 정규 공간 필링 테셀레이션(또는 벌집)이다.
기하학
그것은 각 가장자리 둘레에 3개의 순서-7 삼각 타일링{3,7}을 가지고 있다.모든 꼭지점은 극이상(이상적인 경계 너머에 존재)이며, 각 꼭지점 주위에 무한히 많은 삼각형 기울기가 헵탄 타일링 정점 그림으로 존재한다.
 푸앵카레 디스크 모델 |  이상적인 표면 |  선택적 셀이 표시된[1] 위쪽 절반 공간 모형 |
관련 폴리탑 및 허니컴
이것은 일련의 자기 이중 정기 꿀벌의 일부분이다: {p,7,p}.
이것은 순서가 7개인 삼각형 타일링 셀이 있는 일반 허니콤의 일부분이다: {3,7,p}.
그것은 헵타의 각형 타일링 정점을 가진 일련의 정규 꿀콤의 일부분이다: {p,7,3}.
순서-7-4 삼각 벌집
| 순서-7-4 삼각 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {3,7,4} |
| 콕시터 도표 | |
| 세포 | {3,7} |
| 얼굴 | {3} |
| 에지 피겨 | {4} |
| 정점수 | {7,4} r{7,7}  |
| 이중 | {4,7,3} |
| 콕시터군 | [3,7,4] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서 7-4 삼각형 벌집(또는 3,7,4 벌집)은 슐래플리 기호 {3,7,4}이(가) 있는 정규 공간 필링 테셀레이션(또는 벌집)이다.
그것은 각 가장자리 둘레에 각각 {3,7}의 4개의 순서-7 삼각형 기울기를 가지고 있다.모든 정점은 (이상적인 경계를 넘어 존재하는) 초이상적이며, 순서 4 육각 타일링 정점 배열로 각 정점 주위에 무한히 많은 순서 7 삼각 기울기가 존재한다.
 푸앵카레 디스크 모델 |  이상적인 표면 |
슐래플리 기호 {3,71,1}, 콕시터 도표 , 순서 7 삼각형 타일링 셀의 종류나 색상이 번갈아 가며 균일한 벌집형으로서 두 번째 구조를 가지고 있다.Coxeter 표기법에서 절반 대칭은 [3,7,4,1+] = [3,71,1]이다.
순서-7-5 삼각 벌집
| 순서-7-5 삼각 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {3,7,5} |
| 콕시터 도표 | |
| 세포 | {3,7} |
| 얼굴 | {3} |
| 에지 피겨 | {5} |
| 정점수 | {7,5} |
| 이중 | {5,7,3} |
| 콕시터군 | [3,7,5] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서 7-3 삼각형 벌집(또는 3,7,5 벌집)은 슐래플리 기호 {3,7,5}이(가) 있는 정규 공간 필링 테셀레이션(또는 벌집)이다.그것은 각 가장자리 둘레에 5개의 순서-7 삼각 타일링, {3,7}을(가)모든 정점은 (이상적인 경계를 넘어 존재하는) 초이상적인 것으로, 순서 5 헵타의 타일링 정점 그림에서 각 정점 주위에 존재하는 순서 7 삼각 기울기가 무한히 많다.
 푸앵카레 디스크 모델 |  이상적인 표면 |
순서-7-6 삼각 벌집
| 순서-7-6 삼각 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {3,7,6} {3,(7,3,7)} |
| 콕시터 도표 | |
| 세포 | {3,7} |
| 얼굴 | {3} |
| 에지 피겨 | {6} |
| 정점수 | {7,6} {(7,3,7)} |
| 이중 | {6,7,3} |
| 콕시터군 | [3,7,6] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서 7-6 삼각형 벌집(또는 3,7,6 벌집)은 슐래플리 기호 {3,7,6}이(가) 있는 정규 공간 필링 테셀레이션(또는 벌집)이다.그것은 각 가장자리 주위에 무한히 많은 순서의 7개의 삼각 타일링, {3,7}을(를)모든 꼭지점은 매우 이상적이며(이상적인 경계를 넘어 존재한다) 순서 6 헵탄 타일링, {7,6}정점 그림에서 각 꼭지점 주위에 무한히 많은 순서 7 삼각형 기울기가 존재한다.
 푸앵카레 디스크 모델 |  이상적인 표면 |
순서-7-무한 삼각 벌집
| 순서-7-무한 삼각 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {3,7,∞} {3,(7,∞,7)} |
| 콕시터 도표 | |
| 세포 | {3,7} |
| 얼굴 | {3} |
| 에지 피겨 | {∞} |
| 정점수 | {7,∞} {(7,∞,7)} |
| 이중 | {∞,7,3} |
| 콕시터군 | [∞,7,3] [3,((7,∞,7))] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서-7-무한 삼각형 벌집(3,7,7,370개 벌집)은 슐래플리 기호 {3,7,196}이(가) 있는 정규 공간 필링 테셀레이션(또는 벌집)이다.그것은 각 가장자리 주위에 무한히 많은 순서의 7개의 삼각 타일링, {3,7}을(를)모든 꼭지점은 매우 이상적이며(이상적인 경계를 넘어 존재한다) 무한히 많은 순서-7 삼각형 기울기가 각 꼭지점 주위에 존재하며, 무한히 순서의 헵각형 타일링, {7,420}, 꼭지점 그림이다.
 푸앵카레 디스크 모델 |  이상적인 표면 |
슐래플리 기호 {3, (7,162,7)}, 콕시터 다이어그램 = , 순서 7 삼각형 타일링 셀의 종류나 색상이 번갈아 나타나는 균일한 벌집형으로서 두 번째 구조를 가지고 있다.Coxeter 표기법에서 절반 대칭은 [3,7,196,1+] = [3,(7,196,7)]이다.
주문-7-3 제곱 벌집
| 주문-7-3 제곱 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {4,7,3} |
| 콕시터 다이어그램 | |
| 세포 | {4,7}  |
| 얼굴 | {4} |
| 정점수 | {7,3} |
| 이중 | {3,7,4} |
| 콕시터군 | [4,7,3] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서-7-3 제곱 벌집(또는 4,7,3 벌집)은 일정한 공간을 채우는 테셀레이션(또는 벌집)이다.각각의 무한 셀은 정점이 2-하이퍼사이클에 놓여 있는 헵탄형 타일링으로 구성되며, 각 타일링에는 이상적인 구체에 제한적인 원이 있다.
order-7-3 제곱 벌집의 슐래플리 기호는 {4,7,3}이며, 각 가장자리마다 head-4 헵타각 기울기 3개가 만난다.이 벌집의 꼭지점은 헵탄형 타일링, {7,3}이다.
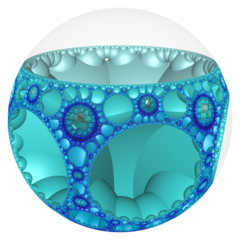 푸앵카레 디스크 모델 |  이상적인 표면 |
오더-7-3 오각형 벌집
| 오더-7-3 오각형 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {5,7,3} |
| 콕시터 다이어그램 | |
| 세포 | {5,7}  |
| 얼굴 | {5} |
| 정점수 | {7,3} |
| 이중 | {3,7,5} |
| 콕시터군 | [5,7,3] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서-7-3 오각형 벌집(5,7,3 벌집)은 일정한 공간을 채우는 테셀레이션(또는 벌집)이다.각각의 무한 셀은 오더-7 오각형 타일링으로 구성되며, 그 정점은 2-하이퍼사이클에 있으며, 각각 이상적인 구위에 제한 원이 있다.
순서 6-3 오각형 벌집의 슐래플리 기호는 {5,7,3}이며, 각 가장자리마다 오더-7 오각형 기울기가 3개씩 만난다.이 벌집의 꼭지점은 헵탄형 타일링, {7,3}이다.
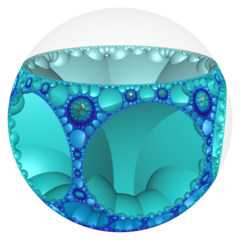 푸앵카레 디스크 모델 |  이상적인 표면 |
순서-7-3 육각형 벌집
| 순서-7-3 육각형 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {6,7,3} |
| 콕시터 다이어그램 | |
| 세포 | {6,7}  |
| 얼굴 | {6} |
| 정점수 | {7,3} |
| 이중 | {3,7,6} |
| 콕시터군 | [6,7,3] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서-7-3 육각형 벌집(또는 6,7,3 벌집)은 일정한 공간을 채우는 테셀레이션(또는 벌집)이다.각 무한 셀은 정점이 2-하이퍼사이클에 놓여 있는 순서 6 육각 타일링으로 구성되며, 각 타일링에는 이상적인 구체에 제한 원이 있다.
order-7-3 육각형 벌집의 슐레플리 기호는 {6,7,3}이며, 각 가장자리에서 3개의 순서-5 육각형 기울기가 만난다.이 벌집의 꼭지점은 헵탄형 타일링, {7,3}이다.
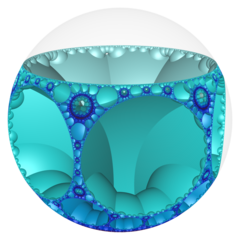 푸앵카레 디스크 모델 | 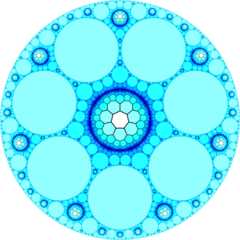 이상적인 표면 |
주문-7-3 아페이로겐 벌집
| 주문-7-3 아페이로겐 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {∞,7,3} |
| 콕시터 다이어그램 | |
| 세포 | {∞,7}  |
| 얼굴 | 아페이로곤 {∞} |
| 정점수 | {7,3} |
| 이중 | {3,7,∞} |
| 콕시터군 | [∞,7,3] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서-7-3 apirogonal honeycomb(또는 or,7,3 honeycomb) 정규 공간 채우기 테셀레이션(또는 honeycomb)이다.각각의 무한 셀은 2-하이퍼사이클에 정점이 놓여 있는 순서-7 a페이로겐 타일링으로 구성되며, 각 타일링에는 이상적인 구에 제한 원이 있다.
아페이로겐 타일링 벌집의 슐래플리 기호는 {195,7,3}이며, 각 가장자리마다 오더-7 아페이로겐 기울기가 3개씩 만난다.이 벌집의 꼭지점은 헵탄형 타일링, {7,3}이다.
아래의 "이상 표면" 투영은 H3의 푸앵카레 반공간 모델에서 무한 평면이다.그것은 가장 큰 원 안에 있는 원의 아폴로니안 개스킷 패턴을 보여준다.
 푸앵카레 디스크 모델 |  이상적인 표면 |
주문-7-4 제곱 벌집
| 주문-7-4 제곱 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {4,7,4} |
| 콕시터 도표 | |
| 세포 | {4,7}  |
| 얼굴 | {4} |
| 에지 피겨 | {4} |
| 정점수 | {7,4} |
| 이중 | 자화자기의 |
| 콕시터군 | [4,7,4] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서-7-4 제곱 벌집(또는 4,7,4 벌집) 슐래플리 기호 {4,7,4}이(가) 있는 정규 공간 채우기 테셀레이션(또는 벌집)을 사용한다.
모든 정점은 (이상적인 경계를 넘어 존재하는) 초이상적이며, 각 가장자리 주위에 네 개의 순서-5 제곱 기울기가 존재하며 순서 4 헵탄형 타일링 정점 그림이 있다.
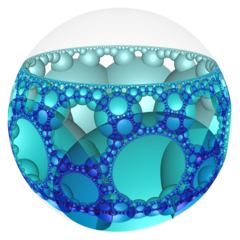 푸앵카레 디스크 모델 | 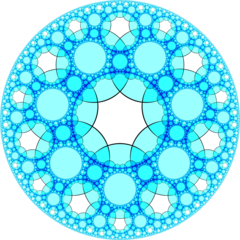 이상적인 표면 |
오더-7-5 오각형 벌집
| 오더-7-5 오각형 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {5,7,5} |
| 콕시터 도표 | |
| 세포 | {5,7}  |
| 얼굴 | {5} |
| 에지 피겨 | {5} |
| 정점수 | {7,5} |
| 이중 | 자화자기의 |
| 콕시터군 | [5,7,5] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서-7-5 오각형 벌집(또는 5,7,5 벌집) 슐래플리 기호 {5,7,5}이(가) 있는 정규 공간 필링 테셀레이션(또는 벌집)이다.
모든 정점은 (이상적인 경계를 넘어 존재하는) 초이상적이며, 각 가장자리 주위에 5개의 순서-7 오각형 기울기가 존재하며, 순서-5 헵타각 타일링 정점 그림이 있다.
 푸앵카레 디스크 모델 |  이상적인 표면 |
순서-7-6 육각형 벌집
| 순서-7-6 육각형 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {6,7,6} {6,(7,3,7)} |
| 콕시터 도표 | |
| 세포 | {6,7}  |
| 얼굴 | {6} |
| 에지 피겨 | {6} |
| 정점수 | {7,6} {(5,3,5)} |
| 이중 | 자화자기의 |
| 콕시터군 | [6,7,6] [6,((7,3,7))] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서 7-6 육각형 벌집(또는 6,7,6 벌집)은 슐래플리 기호 {6,7,6}이(가) 있는 정규 공간 필링 테셀레이션(또는 벌집)이다.각 가장자리 둘레에 오더-7 육각 틸팅 {6,7}이(가) 있다.모든 정점은 (이상적인 경계를 넘어 존재하는) 초이상적인 것으로, 순서에 따라 6각형 기울기가 각 정점 주위에 무한히 많이 존재한다.
 푸앵카레 디스크 모델 | 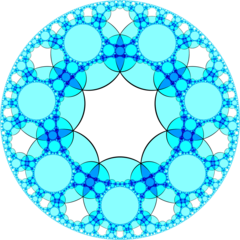 이상적인 표면 |
균일한 벌집형, 슐래플리 기호 {6, (7,3,7)}, 콕세터 도표로서 세포의 종류나 색상이 교대로 되어 있는 두 번째 구조를 가지고 있다.Coxeter 표기법에서 절반 대칭은 [6,7,6,1+] = [6,7,7]이다.
주문-7-무한 아페이로겐 벌집
| 주문-7-무한 아페이로겐 벌집 | |
|---|---|
| 유형 | 일반 벌집 |
| 슐레플리 기호 | {∞,7,∞} {∞,(7,∞,7)} |
| 콕시터 도표 | |
| 세포 | {∞,7}  |
| 얼굴 | {∞} |
| 에지 피겨 | {∞} |
| 정점수 | |
| 이중 | 자화자기의 |
| 콕시터군 | [∞,7,∞] [∞,((7,∞,7))] |
| 특성. | 정규 |
쌍곡선 3-공간 기하학에서 순서-7-무한 아페이로겐 벌집(또는 ∞,7,∞,∞)은 슐래플리 기호가 {,,7,∞}인 정규 공간 채우기 테셀레이션(또는 벌집)이다.그것은 무한히 많은 오더-7 apirogonal tiling{17}을 각 가장자리에 가지고 있다.모든 정점은 무한히 많은 순서가 있는 초이상적(이상적 경계 너머에 존재함)이다-7 무한정 순서의 각 정점 주위에 존재하는 페이로겐 기울기.
 푸앵카레 디스크 모델 |  이상적인 표면 |
균일한 벌집형, 슐레플리 기호 {∞, (7,164,7)}, 콕세터 도표로서 세포의 종류나 색상이 교대로 되어 있는 두 번째 구조를 가지고 있다.
참고 항목
참조
- Coxeter, 일반 폴리토페즈, 3번째, Dover Publishments, 1973. ISBN0-486-61480-8. (테이블 I 및 II: 일반 폴리탑 및 허니컴, 페이지 294–296)
- 기하학의 아름다움: 12개의 에세이(1999), 도버 출판물, LCCN 99-35678, ISBN 0-486-40919-8 (10장, 쌍곡 공간의 일반 허니컴) 표 III
- 제프리 R. Weeks The Shape of Space, 제2판 ISBN 0-8247-0709-5 (제16장–17장: 3-manifolds I,II)
- 조지 맥스웰, 스피어패킹 및 쌍곡반사 그룹, 저널 오브 대수학 79,78-97 (1982) [1]
- Hao Chen, Jean-Philipe Labbé, Lorenzian Coxeter 그룹 및 Boyd-Maxwell 볼 패킹, (2013)[2]
- 하이퍼볼릭 허니컴 arXiv 시각화:1511.02851 Roice Nelson, Henry Segman(2015)
외부 링크
- 쌍곡선 카타콤스 캐러셀: {3,7,3} 벌집형 유튜브, 로이스 넬슨
- 존 배즈, 시각적 통찰력: {7,3,3} 허니콤(2014/08/01) {7,3,3} 허니콤이 인피니티에서 비행기를 만나다(2014/08/14)
- Danny Calegari, Kleinian은 2014년 3월 4일 Kleinian 그룹의 시각화 도구인 Geometry와 Imagination을 사용한다.[3]


