직교 함수

수학에서 직교 함수는 이선형 형태를 갖춘 벡터 공간인 함수 공간에 속한다. 함수 공간에 간격이 도메인으로 있는 경우, 이선형 형태는 그 간격에 걸쳐 함수 산출물의 정수일 수 있다.

${\displaystyle \langle f,g\angle =\int {\overline {f(x)}g(x)\,dx.}$

The functions ${\displaystyle f}$ and ${\displaystyle g}$ are orthogonal when this integral is zero, i.e. ${\displaystyle \langle f,\,g\rangle =0}$ whenever ${\displaystyle f\neq g}$. As with a basis of vectors in a finite-dimensional space, orthogonal functions can form an infinite basis for a funct이온 공간 개념적으로 위의 적분은 벡터 도트-제품과 동등하다. 두 벡터는 도트-제품이 0이면 상호 독립적이다(직교).

조금이라도 L2-norms의 직교 함수의 Suppose{f0, f1, …}{\displaystyle\와 같이{f_{0},f_{1},\ldots)}}시퀀스 ‖ fn‖ 2)⟨ f, fn⟩)(∫ fn2d))12{\textstyle\left\ f_{n}\right\ _{2}={\sqrt{\langle f_{n},f_{n}\rangle}}=\left(\int f_{n}^{2}\dx\right)^{\frac{1.}${{2$$\}\}\}\}\}$ {${\displaystyle f_{}}$ n /${\displaystyle {}_{}\Vert {}_{}}$ ${\displaystyle {f_{}}_{}}$ ${\displaystyle {{}_{}}_{}}$ ${\displaystyle {}_{}}$ ${\$f_${n$}/\$f_{$n}\f_{$n}\right\ _${2}\right$\}}}}}}}}}}$ 순서는 L-norm² 1의 함수로서$$ 직교 순서를 형성하고 있다. 정의된 L-표준을² 가지려면 적분 범위를 제한해야 하며, 이는 함수를 제곱-적분성을 제한한다.

삼각함수

직교 함수의 몇 세트가 근사 함수의 표준 기준이 되었다. 예를 들어 sine 함수 sinnnx와 sin mx는 $m{\displaystyle \mathrm{nn}}$( -${\displaystyle \pi }$ ,$){\displaystyle x\in (-\pi ,\pi )}$ 간격 x ${\displaystyle \in }$(-\$displaystyle m\neq n})$과 n 및 m이 양의 정수인 경우$$ 직교한다. 그때를 위해

${\displaystyle 2\sin \left(mx\right)\sin \left(nx\right)=\cos \left(\왼쪽(m-n\right)-\cos \left(m+n\rig)x\right),}$

두 사인 함수의 제품의 적분은 사라진다.^[1] 코사인 기능과 함께, 이러한 직교 함수는 푸리에 시리즈와의 간격에서 주어진 함수의 근사치를 위해 삼각 다항식으로 조립될 수 있다.

다항식

만일 하나가 [${\displaystyle }$- ${\displaystyle 1}$, ${\displaystyle 1\mathrm{}}$${\displaystyle }$,${\displaystyle x}$, ${\displaystyle {x\mathrm{}}^{}}$ ${\displaystyle {}^{}}$,${\displaystyle \dots ]}$의 간격에$$ 있는 단항 순서${\$$x$$,x^{2$$},\dots$$\right$$\}}}$에서 시작하여 Gram-Schmidt 프로세스를 적용하면, 그램-Schmidt를 얻는다. 직교 다항식의 또 다른 모음은 연관된 범례 다항식이다.

직교 다항식 연구는 양면 형태에 삽입된$$ $w{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle w(x)}$의 중량 함수를 포함한다.

${\displaystyle \langle f,g\angle =\int w(x)f(x)g(x)\,dx.}$

$({\displaystyle 0}$, ${\displaystyle \mathrm{\infty }}$) ${\displaystyle (0,\inflt )}$의 Laguerre 다항식의 경우 중량$$ 함수는 $w{\displaystyle }$( x${\displaystyle }$)${\displaystyle }$= ${\displaystyle {}^{}}$- ${\displaystyle x^{}}$ ${\$w$(x)=e^{-x}}$이다$.$

Both physicists and probability theorists use Hermite polynomials on ${\displaystyle (-\infty ,\infty )}$, where the weight function is ${\displaystyle w(x)=e^{-x^{2}}}$ or ${\displaystyle w(x)=e^{-x^{2}/2}}$.

Chebyshev polynomials are defined on ${\displaystyle [-1,1]}$ and use weights ${\textstyle w(x)={\frac {1}{\sqrt {1-x^{2}}}}}$ or ${\textstyle w(x)={\sqrt {1-x^{2}}}}$.

제르니케 다항식은 단위 디스크에 정의되며 방사형 및 각도 부분 모두의 직교성을 가진다.

이진수치함수

월시 함수와 하르 파장은 이산 범위를 갖는 직교 함수의 예다.

이성 함수

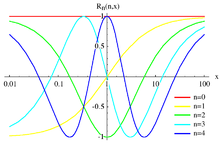
레전드르와 체비셰프 다항식은 [-1, 1] 간격 동안 직교 패밀리를 제공하며, 때때로 [0, ∞]에 직교 패밀리가 필요하다. 이 경우, Cayley 변환을 먼저 적용하여 [-1, 1]로 주장을 이끌어 내는 것이 편리하다. 이 절차는 레전드르 이성적 함수와 체비셰프 이성적 함수로 불리는 이성적 직교 함수의 패밀리를 초래한다.

미분 방정식에서

경계 조건이 있는 선형 미분 방정식의 해법은 직교 용액 함수의 가중 합계(예: 고유함수)로 쓰여 푸리에 시리즈를 일반화시킬 수 있다.

참고 항목

• 고유값 및 고유 벡터
• 힐베르트 공간
• 카루넨-로이브 정리
• 로리첼라의 정리
• 직교 명령 집합
• 와니어 함수

참조

• 조지 B. Arfken & Hans J. Weber(2005) 물리학을 위한 수학 방법, 6판, 10장: Sturm-Louville 이론 - 직교 함수, 학술적 언론.
• Price, Justin J. (1975). "Topics in orthogonal functions". American Mathematical Monthly. 82: 594–609. doi:10.2307/2319690.
• Giovanni Sansone (Ainsley H. Diamond에 의해 번역됨) (1959년) 직교 함수, 인터사이언스 출판사.

외부 링크

• 직교 함수, MathWorld.