모션 플래닝

Motion planning

모션 플래닝은 경로 플래닝(내비게이션 문제 또는 피아노 무버의 문제라고도 함)은 객체를 소스에서 대상으로 이동하는 일련의 유효한 구성을 찾기 위한 계산 문제입니다.이 용어는 컴퓨터 기하학, 컴퓨터 애니메이션, 로봇 공학 및 컴퓨터 게임에 사용됩니다.

예를 들어, 건물 내부의 모바일 로봇을 먼 경유지로 이동하는 것을 고려해 보십시오.벽을 피하고 계단에서 떨어지지 않으면서 이 작업을 수행해야 한다.모션 플래닝 알고리즘은 이러한 작업에 대한 설명을 입력으로 받아들여 로봇의 휠에 전송되는 속도와 회전 명령을 생성합니다.모션 계획 알고리즘은 더 많은 관절 수(예: 산업용 조작기), 더 복잡한 작업(예: 물체의 조작), 다른 제약 조건(예: 앞쪽으로만 주행할 수 있는 자동차) 및 불확실성(예: 환경 또는 로봇의 불완전한 모델)을 가진 로봇을 다룰 수 있다.

모션 플래닝에는 CAD 소프트웨어의 자율성, 자동화 및 로봇 설계와 같은 여러 로봇 애플리케이션뿐만 아니라 디지털 캐릭터 애니메이션, 비디오 게임, 건축 디자인, 로봇 수술 및 생물학적 분자 연구와 같은 다른 분야의 애플리케이션도 있습니다.

개념

워크스페이스의 예.
점 크기 로봇의 구성 공간입니다.흰색 = Cfree, 회색 = Cobs.
직사각형 변환 로봇을 위한 구성 공간(빨간색 사진).흰색 = Cfree, 회색 = Cobs. 여기서 어두운 회색 = 물체, 밝은 회색 = 로봇이 물체를 만지거나 작업 공간을 벗어날 수 있는 구성입니다.
유효한 경로의 예.
유효하지 않은 경로의 예.
로드맵의 예시.

기본 모션 플래닝 문제는 기존의 장애물과의 충돌을 피하면서 스타트 구성 S와 목표 구성 G를 접속하는 연속 경로를 계산하는 것이다.로봇 및 장애물 형상은 2D 또는 3D 작업 공간에서 설명되며, 모션은 (아마도 더 높은 차원) 구성 공간에서 경로로 표시됩니다.

구성 공간

구성은 로봇의 자세를 기술하며 구성 공간 C는 가능한 모든 구성의 집합입니다.예를 들어 다음과 같습니다.

  • 로봇이 2차원 평면(작업 공간)에서 변환하는 단일 지점(0-사이즈)인 경우 C는 평면이며 두 개의 파라미터(x, y)를 사용하여 구성을 나타낼 수 있습니다.
  • 로봇이 변환하고 회전할 수 있는 2D 모양인 경우 작업 공간은 여전히 2차원입니다.단, C는 특수 유클리드 그룹 SE2(2) R × { \times} SO(2)이며, 여기서 SO(2)는 특수 직교 그룹이며, 3개의 파라미터(x, y, θ)를 사용하여 구성을 나타낼 수 있다.
  • 로봇이 변환 및 회전이 가능한 입체 3D 모양인 경우 작업 공간은 3차원이지만, C는 특수 유클리드 그룹 SE(3) =R3× {\ SO(3)이며, 구성에는 변환에 (x, y, z) 및 오일러 각도(α, β, β)의 6개 파라미터가 필요합니다.
  • 로봇이 N개의 회전식 조인트를 가진 고정 기반 조작기(폐쇄 루프 없음)인 경우 C는 N차원입니다.

빈 공간

장애물과의 충돌을 회피하는 설정 세트를 프리 스페이스free C라고 부릅니다.C에서 C의 보완을free 장애물 또는 금지 영역이라고 합니다.

종종 C의 형상을free 명시적으로 계산하기가 매우 어렵다.단, 특정 Configuration이 C에 있는지free 여부를 테스트하는 것은 효율적입니다.첫째, 전방 운동학은 로봇의 지오메트리의 위치를 결정하고 로봇의 지오메트리가 환경의 지오메트리와 충돌할 경우 충돌 감지 테스트를 수행합니다.

대상 공간

대상 공간은 로봇이 이동할 위치를 나타내는 여유 공간의 하위 공간입니다.글로벌 모션 계획에서 목표 공간은 로봇의 센서에 의해 관찰됩니다.그러나 로컬 모션 계획에서는 로봇이 일부 상태에서는 대상 공간을 관찰할 수 없습니다.이 문제를 해결하기 위해 로봇은 여러 가상 대상 공간을 통과하며, 각 가상 대상 공간은 관찰 가능한 영역(로봇 주변) 내에 위치합니다.가상 대상 공간을 하위 목표라고 합니다.

장애물 공간

장애물 공간은 로봇이 이동할 수 없는 공간입니다.장애물 공간은 여유 공간과 반대되는 것이 아닙니다.

알고리즘

저차원 문제는 구성 공간 위에 그리드를 오버레이하는 그리드 기반 알고리즘이나 C의free 모양과 연결성을 계산하는 기하학적 알고리즘으로 해결할 수 있습니다.

복잡한 제약 조건 하에서 고차원 시스템에 대한 정확한 모션 계획은 계산적으로 다루기 어렵습니다.전위장 알고리즘은 효율적이지만 로컬 최소값의 대상이 됩니다(단, 고조파 전위장은 예외입니다).샘플링 기반 알고리즘은 로컬 최소값 문제를 방지하고 많은 문제를 매우 빠르게 해결합니다.패스가 존재하지 않는다고 판단할 수는 없지만 시간이 지날수록 실패 확률이 0으로 감소합니다.

샘플링 기반 알고리즘은 현재 고차원 공간에서 모션 플래닝의 최첨단 기술로 간주되며 수십 또는 수백 개의 차원을 가진 문제(로봇 조작기, 생물 분자, 애니메이션 디지털 캐릭터 및 다리 로봇)에 적용되어 왔다.

(비행하는 물체를 잡기 위한) 물체 조작을 위한 모션 플래닝 병렬 알고리즘(A1-A2)이 있습니다.[1]

그리드 기반 검색

그리드 기반 접근방식은 구성 공간에 그리드를 오버레이하고 각 구성이 그리드 포인트로 식별된다고 가정합니다.각 그리드 포인트에서free 로봇은 인접한 그리드 포인트로 이동할 수 있습니다(충돌 감지와 함께 테스트됨).이것에 의해, 일련의 액션이 이산화 되어, 검색 알고리즘(A*등)이 개시로부터 목표까지의 패스를 검출하기 위해서 사용됩니다.

이러한 접근방식을 사용하려면 그리드 분해능을 설정해야 합니다.거친 그리드를 사용하면 검색이 더 빨라지지만 알고리즘은 C의 좁은free 부분을 통과하는 경로를 찾지 못합니다.또, 그리드상의 점수는 구성 공간 치수로 기하급수적으로 증가하기 때문에, 고차원적인 문제에 적합하지 않다.

기존의 그리드 기반 접근법은 주어진 기준 각도의 배수로 표제 변경이 제한되는 경로를 생성하며, 종종 차선의 경로를 초래한다.임의의 각도 경로 계획 접근 방식은 그리드 가장자리에 대한 경로를 제한하지 않고 그리드 가장자리를 따라 정보를 전파하여 짧은 경로를 찾습니다.

예를 들어, 구성 공간에 대한 로봇의 지식이 변경되거나 경로 추종 중에 구성 공간 자체가 변경되는 경우 그리드 기반 접근 방식은 종종 반복적으로 검색해야 합니다.증분 휴리스틱 검색 알고리즘은 이전의 유사한 경로 계획 문제에 대한 경험을 활용하여 빠르게 재설계하여 현재 경로 계획에 대한 검색 속도를 높입니다.

간격 기반 검색

이러한 접근방식은 그리드 [2]대신 구성 공간 전체를 포괄하는 포장을 생성한다는 점을 제외하면 그리드 기반 검색 접근방식과 유사합니다.포장은 X cfree C x+ X와− 같이 박스로 만들어진 2개의 서브포장− X,X로+ 분해된다.C의 특성을 파악하면free 설정된 반전 문제를 해결할 수 있다.따라서 C가 보장된 인클로저를 가지기 위해 선형 부등식으로 설명할 수 없는 경우 구간free 분석을 사용할 수 있다.

따라서 로봇은 X 내에서 자유롭게− 이동할 수 있으며 X 밖으로+ 나갈 수 없습니다.양쪽 서브패빙에서 네이버그래프가 구축되어 Dijkstra 또는 A* 등의 알고리즘을 사용하여 경로를 찾을 수 있습니다.패스가 X 로 실현− 가능한 경우는, C 로도free 실현 가능합니다.1개의 초기 설정에서 목표까지의 경로가 X에+ 존재하지 않는 경우 C에 실현free 가능한 경로가 존재하지 않음을 보증합니다.그리드 기반 접근법에 대해서는 생성되는 상자의 수가 구성 공간의 치수에 비해 기하급수적으로 증가하므로 간격 접근법은 고차원 문제에 적합하지 않다.

2개의 자유도를 가진 훅을 왼쪽에서 오른쪽으로 이동시켜 수평으로 작은 세그먼트 2개를 피해야 하는 오른쪽의 3개의 그림에서 그림을 볼 수 있습니다.

초기 구성(파란색)에서 후크의 최종 구성으로 이동하여 2개의 장애물(빨간색 세그먼트)을 회피합니다.후크의 왼쪽 하단 모서리는 수평선에 있어야 하며, 후크는 2도 자유도가 됩니다.
구성 공간을 덮는 상자에 의한 분해:하위 포장− X는 모두 빨간색 상자이고 하위 포장+ X는 빨간색 상자 및 녹색 상자입니다.경로는 위에 표시된 움직임에 해당합니다.
이 그림은 위와 같은 경로에 해당하지만 상자 수는 훨씬 적습니다.이 알고리즘은 최종 결과에 영향을 주지 않는 구성 공간의 일부에서 상자를 이등분하지 않도록 합니다.

구간 분석을 사용하여 서브파빙을 분해함으로써 연결된 컴포넌트의 [3]수를 카운트하는 등 C의free 토폴로지를 특성화할 수도 있습니다.

기하 알고리즘

다각형 장애물 사이에 로봇을 배치하다

장애물 간 객체 변환

건물 밖으로 나가는 길 찾기

  • 가장 먼 광선 추적

현재 위치 주변의 광선 다발이 벽에 닿으면 도어가 식별되지 않는 한 로봇은 가장 긴 광선의 방향으로 이동한다.이러한 알고리즘은 건물로부터의 비상 탈출을 모델링하기 위해 사용되었다.

인공 전위장

한 가지 방법은 로봇의 구성을 목표에 대한 끌어당김과 장애물에 대한 거부감을 결합하는 잠재적 영역의 한 지점으로 취급하는 것입니다.결과 궤적은 경로로 출력됩니다.이 접근법은 궤적이 거의 계산되지 않고 생성된다는 점에서 장점이 있다.단, 포텐셜필드의 로컬최소값에 갇히거나 경로를 찾지 못하거나 최적 경로가 아닌 경로를 찾을 수 있습니다.인공 전위장은 정전 전위장과 유사한 연속체 방정식으로 처리하거나(로봇을 점전하처럼 처리), 일련의 언어 [4]규칙을 사용하여 필드를 통과하는 움직임을 이산화할 수 있습니다.항법[5] 함수 또는 확률론적 항법[6] 함수는 목표 지점을 제외하고 최소 지점을 가지지 않는 품질을 가진 일종의 인공 잠재력 함수입니다.

샘플링 기반 알고리즘

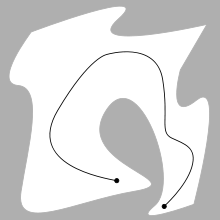
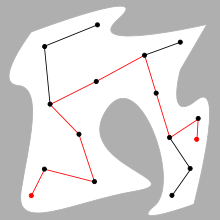
샘플링 기반 알고리즘은 샘플링된 구성의 로드맵을 사용하여 설정 공간을 나타냅니다.기본 알고리즘은 C의 N개의 Configuration을 샘플링하여 C의free Configuration을 마일스톤으로 사용합니다.다음으로 선분 PQ가 완전히 C에 있는free 경우 2개의 마일스톤 P와 Q를 연결하는 로드맵이 작성됩니다.다시, 충돌 검출은 C에 포함되는free 것을 테스트하기 위해 사용됩니다.S와 G를 연결하는 경로를 찾기 위해 로드맵에 추가됩니다.로드맵의 경로가 S와 G를 링크하는 경우 플래너는 성공하고 해당 경로를 반환합니다.그렇지 않은 경우 원인은free 명확하지 않습니다.C에 경로가 없거나 플래너가 충분한 마일스톤을 샘플링하지 않았기 때문입니다.

이들 알고리즘은 조합 알고리즘과 달리 C의 치수에 따라 (명시적으로) 기하급수적으로 의존하지 않기 때문에 고차원 구성 공간에서 잘 작동합니다.또, (일반적으로) 실장도 상당히 간단합니다.이 값은 확률적으로 완전합니다. 즉, 시간이 더 오래 걸릴수록 솔루션을 생성할 확률이 1에 가깝습니다.그러나 솔루션이 존재하지 않는지 여부를 판단할 수 없습니다.

C의 기본적인free 가시성 조건을 고려할 때 구성 수 N이 증가할수록 위의 알고리즘이 솔루션을 찾을 확률은 기하급수적으로 [7]1에 가깝다는 것이 증명되었습니다.가시성은 C의 치수에 따라 명시적으로 좌우되지 않으며, 가시성이 좋은 고차원 공간 또는 가시성이 나쁜 저차원 공간을 가질 수 있습니다.표본 기반 방법의 실험적인 성공은 일반적으로 볼 수 있는 대부분의 공간이 가시성이 우수하다는 것을 나타냅니다.

이 기본 스킴에는 다음과 같은 다양한 종류가 있습니다.

  • 일반적으로 모든 쌍보다 가까운 이정표 쌍 사이의 세그먼트만 테스트하는 것이 훨씬 빠르다.
  • 불균일한 샘플링 분포는 로드맵의 연결을 개선하는 영역에 더 많은 이정표를 배치하려고 시도합니다.
  • 일부 최근의 연구는 무작위성 원천의 영향이 표본 분포의 효과에 비해 미미하다고 주장하지만, 준난수 표본은 일반적으로 의사 난수 표본보다 더 나은 구성 공간의 덮개를 생성한다.
  • 국지적 제안 분포와 함께 방향성 마르코프 연쇄 몬테카를로 랜덤 워크를 수행하여 국지적 샘플링을 사용한다.
  • 곡선 시야를 허용함으로써[9](예를 들어 두 이정표 사이의 길을 막는 장애물을 기어감으로써) 주어진 문제를 해결하는 데 필요한 이정표 수를 상당히 줄일 수 있다.
  • 계획 쿼리가 1개 또는 몇 개만 필요한 경우 공간 전체의 로드맵을 작성할 필요가 없습니다.일반적으로 이 경우 트리 성장 변형이 더 빠릅니다(단일 쿼리 계획).로드맵은 동일한 공간에서 많은 쿼리를 수행하는 경우에도 유용합니다(멀티 쿼리 계획).

주목할 만한 알고리즘 목록

완전성과 퍼포먼스

모션 플래너는 한정된 시간 내에 해결책을 제시하거나 해결책이 없다고 올바르게 보고하면 완성이라고 합니다.대부분의 완전한 알고리즘은 지오메트리 기반입니다.완전한 계획자의 성과는 계산의 복잡성에 의해 평가됩니다.이 성질을 수학적으로 증명할 때는 점근 한계뿐만 아니라 유한한 시간 내에 발생하는지 확인해야 합니다.이것은 특히 문제가 됩니다.특정 증명 기술 중에 무한 시퀀스(한계 케이스에서만 수렴)가 발생하면 그 이후 이론적으로 알고리즘은 정지하지 않습니다.직관적인 "꼼수"(종종 유도 기반)는 일반적으로 무한 한도에 대해서만 수렴하는 것으로 잘못 생각됩니다.즉, 해결책은 존재하지만 플래너는 절대 보고하지 않습니다.따라서 이 속성은 튜링 완전성과 관련이 있으며 대부분의 경우 이론적인 기초/지침으로 작용한다.무차별 포스 접근법에 기초한 플래너는 항상 완전하지만 유한하고 이산적인 설정에서만 실현 가능합니다.

실제로 알고리즘의 종료는 카운터를 사용하여 항상 보증할 수 있습니다.카운터는 최대 반복 횟수만 허용하며, 그 후 솔루션 유무에 관계없이 항상 정지합니다.실시간 시스템의 경우 일반적으로 워치독타이머를 사용하면 프로세스가 종료됩니다.워치독은 모든 프로세스로부터 독립적이어야 합니다(일반적으로 낮은 수준의 인터럽트 루틴에 의해 실현됩니다).그러나 이전 단락에서 설명한 점근 케이스는 이 방법으로는 도달하지 못할 것이다.지금까지 발견된 것 중 가장 좋은 것(없음보다 나은 것) 또는 없는 것을 보고하지만, 없는 것을 올바르게 보고할 수는 없습니다.워치독을 포함한 모든 실현은 항상 불완전합니다(단, 모든 경우를 유한시간 내에 평가할 수 있습니다.

완전성은 매우 엄격한 수학적 정확성 증명(종종 도구와 그래프 기반 방법에 의해 지원됨)에 의해서만 제공될 수 있으며, 신청서에 안전 내용이 포함된 경우에만 전문 전문가가 수행해야 한다.한편, 무한 루프 1개 또는 잘못된 결과 1개만 반환하면 되기 때문에 완전성의 반증이 간단합니다.알고리즘의 형식 검증/정확성은 그 자체로 연구 분야입니다.이러한 테스트 케이스를 올바르게 설정하는 것은 매우 고도의 작업입니다.

해상도의 완전성은 기본 그리드의 해상도가 충분히 양호한 경우 플래너가 경로를 찾을 수 있도록 보장되는 속성입니다.대부분의 분해능 완전 플래너는 그리드 기반 또는 간격 기반입니다.분해능 완전 계획자의 계산 복잡도는 기본 그리드의 점 수, 즉 O(1/hd)에 따라 달라진다. 여기서 h는 분해능(그리드 셀의 한쪽 면 길이)이고 d는 구성 공간 치수이다.

확률론적 완전성은 더 많은 "작업"이 수행될수록 설계자가 경로를 찾지 못할 확률이 점근적으로 0에 근접하는 속성이다.몇 가지 샘플 기반 방법이 확률적으로 완전합니다.확률적으로 완전한 계획자의 성과는 수렴률로 측정됩니다.실제 어플리케이션에서는 보통 이 속성을 사용합니다.이는 평균 컨버전스 시간에 따라 워치독의 타임아웃을 설정할 수 있기 때문입니다.

불완전한 계획자가 존재할 때 항상 실현 가능한 경로를 생성하는 것은 아니다(첫 번째 단락 참조).때때로 불완전한 계획자들은 실제로 일을 잘 한다. 왜냐하면 그들은 항상 보장된 시간 후에 멈추고 다른 일상이 이어지도록 하기 때문이다.

문제의 종류

이 기본적인 문제의 변형을 처리하기 위해 많은 알고리즘이 개발되었습니다.

차동 제약

홀로노믹

  • 조작기 암(다이내믹스 포함)

비홀로노믹

  • 드론
  • 자동차
  • 외발자전거
  • 평면
  • 가속 제한 시스템
  • 이동 장애물(시간은 되돌릴 수 없음)
  • 베벨 끝 조종 가능한 바늘
  • 디퍼렌셜 구동 로봇

최적성의 제약

하이브리드 시스템

하이브리드 시스템은 이산적인 동작과 연속적인 동작을 혼합한 시스템입니다.이러한 시스템의 예는 다음과 같습니다.

불확실성

환경상의 제약

  • 다이내믹스 맵

적용들

「 」를 참조해 주세요.

레퍼런스

  1. ^ Bodrenko, A.I. (2019). "New Method Of Using Mobile Robots For Moving Cargo In Warehouse" (PDF). Bulletin of Science and Practice. 5 (6): 192–211. doi:10.33619/2414-2948/43/26. S2CID 196205001.
  2. ^ Jaulin, L. (2001). "Path planning using intervals and graphs" (PDF). Reliable Computing. 7 (1).
  3. ^ Delanoue, N.; Jaulin, L.; Cottenceau, B. (2006). Counting the Number of Connected Components of a Set and Its Application to Robotics (PDF). Applied Parallel Computing, Lecture Notes in Computer Science. Lecture Notes in Computer Science. Vol. 3732. pp. 93–101. CiteSeerX 10.1.1.123.6764. doi:10.1007/11558958_11. ISBN 978-3-540-29067-4.
  4. ^ Wolf, Joerg Christian; Robinson, Paul; Davies, Mansel (2004). "Vector Field path planning and control of an autonomous robot in a dynamic environment". Proc. 2004 FIRA Robot World Congress. Busan, South Korea: Paper 151.
  5. ^ Lavalle, Steven, 계획 알고리즘 8장
  6. ^ Hacohen, Shlomi; Shoval, Shraga; Shvalb, Nir (2019). "Probability Navigation Function for Stochastic Static Environments". International Journal of Control, Automation and Systems. 17 (8): 2097–2113. doi:10.1007/s12555-018-0563-2. S2CID 164509949.
  7. ^ Hsu, D.; J.C. Latombe, J.C.; Motwani, R. (1997). "Path planning in expansive configuration spaces". Proceedings of International Conference on Robotics and Automation. Vol. 3. pp. 2719–2726. doi:10.1109/ROBOT.1997.619371. ISBN 978-0-7803-3612-4. S2CID 11070889.
  8. ^ Lai, Tin; Morere, Philippe; Ramos, Fabio; Francis, Gilad (2020). "Bayesian Local Sampling-Based Planning". IEEE Robotics and Automation Letters. 5 (2): 1954–1961. arXiv:1909.03452. doi:10.1109/LRA.2020.2969145. ISSN 2377-3766. S2CID 210838739.
  9. ^ Shvalb, N.; Ben Moshe, B.; Medina, O. (2013). "A real-time motion planning algorithm for a hyper-redundant set of mechanisms". Robotica. 31 (8): 1327–1335. CiteSeerX 10.1.1.473.7966. doi:10.1017/S0263574713000489. S2CID 17483785.
  10. ^ Scordamaglia, V.; Nardi, V. A. (2021). "A set-based trajectory planning algorithm for a network controlled skid-steered tracked mobile robot subject to skid and slip phenomena". Journal of Intelligent & Robotic Systems. Springer Nature B.V. 101. doi:10.1007/s10846-020-01267-0. S2CID 229326435.
  11. ^ Kucner, Tomasz Piotr; Lilienthal, Achim J.; Magnusson, Martin; Palmieri, Luigi; Srinivas Swaminathan, Chittaranjan (2020). "Probabilistic Mapping of Spatial Motion Patterns for Mobile Robots". Cognitive Systems Monographs. doi:10.1007/978-3-030-41808-3. ISSN 1867-4925.
  12. ^ Steven M. LaValle (29 May 2006). Planning Algorithms. Cambridge University Press. ISBN 978-1-139-45517-6.

추가 정보

외부 링크

Wikimedia Commons에는 모션 플래닝과 관련된 미디어가 있습니다.