투시성
Perspectivity이 기사는 독자들에게 혼란스럽거나 불분명할 수 있다.(2019년 5월 (이 및 ) |
기하학에서 원근법(perspectivity)은 고정된 지점에서 바라본 장면의 화상 평면에서 이미지를 형성하는 것을 말한다.
그래픽스
그래픽 원근법의 과학은 원근법을 사용하여 사실적인 이미지를 적절한 비율로 만듭니다.커스티 안데르센에 따르면, 원근법을 묘사한 최초의 작가는 그의 드 픽투라 (1435)에서 레온 알베르티였다.[1]영어로, 브룩 테일러는 1715년에 그의 선형 원근법을 발표했는데, 그는 "원근법은 기하학의 법칙에 의해 어떤 도형의 외관을 평면 위에 그리는 기술이다."[2]라고 설명했다.두 번째 책, 선형 원근법의 새로운 원리 (1719)에서 테일러는 썼다.
- 그림의 여러 부분에서 특정 법칙에 따라 그려진 선이 평면을 절단하고 해당 절단 또는 교차점에 의해 평면상의 그림이 묘사되는 경우, 이렇게 기술된 그림을 다른 그림의 투영이라고 합니다.이 투영을 만드는 선을 모두 합치면 광선계라고 합니다.그리고 이 모든 광선이 하나의 지점을 통과할 때, 그것들은 원추형 광선이라고 불립니다.그리고 그 점이 '관객의 눈'으로 여겨질 때, 그 광선계를 광학[3] 원뿔이라고 부른다.
투영 형상
투영 기하학에서 선의 점을 투영 범위라고 하며, 점 위의 평면 내 선 집합을 연필이라고 합니다.
투영 평면의 두 선{\({과m({m})과 어느 선상의 점 P가 주어졌을 때 p({ 의 점과 P의 연필 선에 의해 결정되는m({m})의 범위 사이의 생물 매핑을 원근법이라고 한다.(또는 더 정확히는 중앙 [4]P를 중심으로 한 중심 시점).점 X와 Y가 원근법에 의해 관련되어 있음을 나타내기 위해 특별한 기호가 사용되었습니다. . { X \ double Y} 이 표기법에서 원근법의 중심이 P임을 나타내려면 X . \ \ \ \ \ \ \ \ \ { P Y 라고 씁니다
원근법이 존재한다는 것은 대응하는 점이 원근법에 있다는 것을 의미합니다.이중 개념인 축 투시도는 투영 범위에 의해 결정되는 두 연필의 선 사이의 대응입니다.
투사성
두 가지 관점의 구성은 일반적으로 관점이 아닙니다.투시성 또는 둘 이상의 투시성을 투영성이라고 합니다(투사 변환, 투사 콜로네이션 및 호모그래피는 동의어입니다).
모든 파피아 투영 [5]평면에 유지되는 투영성 및 원근법에 관한 몇 가지 결과가 있다.
정리:두 개의 서로 다른 투영 범위 사이의 투영성은 두 개 이상의 관점으로 구성될 수 없습니다.
정리:투영 범위부터 그 자체까지의 투영성은 3가지 관점의 구성이라고 할 수 있습니다.
정리:점을 고정하는 두 개의 서로 다른 투영 범위 사이의 투영성이 관점입니다.
고차원적 전망
어느 선에도 없는 평면의 점에 의해 결정되는 평면의 두 선 위의 점 사이의 쌍방향 대응은 원근법이라고도 하는 고차원 유추체를 가진다.
S와m T를 n차원 투영 공간n R에 포함된 두 개의 구별되는 m차원 투영 공간이라고 하자m.P를 R의n (n - m - 1)차원 부분공간으로 하고n−m−1, S 또는m T와m 공통되는 점이 없다고 하자.S의m 각 점 X에 대해, X와n-m-1 P가 스팬한 공간 L은 점 Y = fP(X)에서 T와 만난다m.이 대응P f는 [6]원근법이라고도 불린다.위에서 설명한 중심 관점은 n = 2 및 m = 1의 경우이다.
투시적 대조
S와2 T를 투영 3공간3 R에서 두 개의 서로 다른 투영 평면이라고 하자2.O와 O*가 어느 평면에서도 R의3 점인 상태에서 마지막 섹션의 구성을 사용하여 중심 O의 원근법에 따라 S를 T에2 투영한2 다음 중심 O*의 원근법에 따라 T를2 S에2 투영합니다.이 구성은 공선점을2 보존하고 투시 콜라인레이션(더 현대적인 [7]용어로 중심 콜라인레이션)이라고 불리는 S의 점들의 그 자체에 대한 생물적 지도이다.be를 S의2 원근법으로 조합한다.S와2 T의2 교차점의 각 점을 and로 고정하고 이 선을 φ의 축이라고 한다.점 P를 선 OO*와 평면2 S의 교차점이라고 하자. 또한 P는 θ로 고정되고 P를 통과하는 모든 S의 선은2 θ로 안정화된다(고정하지만 반드시 점으로 고정되는 것은 아니다).P를 φ의 중심이라고 합니다.P를 통과하지 않는 S의2 라인에 대한 θ의 제한은 그 라인과 θ 아래의 이미지인 라인 사이의 중심 P를 가진 S의 중심2 투시성입니다.
「 」를 참조해 주세요.
메모들
레퍼런스
- Andersen, Kirsti (1992), Brook Taylor's Work on Linear Perspective, Springer, ISBN 0-387-97486-5
- Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50458-0, MR 0123930
- Fishback, W.T. (1969), Projective and Euclidean Geometry, John Wiley & Sons
- Pedoe, Dan (1988), Geometry/A Comprehensive Course, Dover, ISBN 0-486-65812-0
- Young, John Wesley (1930), Projective Geometry, The Carus Mathematical Monographs (#4), Mathematical Association of America
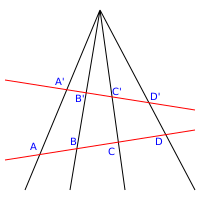


 어느 선상의 점 P가 주어졌을 때
어느 선상의 점 P가 주어졌을 때



