플라나 대수

수학에서 평면알제브라는 처음으로 본 존스의 작품에서 II₁ 하위요인의 표준 불변성에 관한 작품에 등장했다.^[1] 또한 많은 매듭 불변제(특히 존스 다항식)에 적절한 대수적 프레임워크를 제공하며, 엉클 구성에 관한 Kovanov 호몰로지 특성을 기술하는 데 사용되어 왔다.^[2][3]모든 하위 요인 평면 대수학에서는 톰슨 집단의 단일 표현 집단을 제공한다.^[4] 모든 유한군(및 양자 일반화)은 평면대수로 부호화할 수 있다.^[1]

정의

평면 대수학의 개념은 표준 불변성의 도식화된 공리화라고 하는 것이다.^{[1] [5] [6]}

플라나르 엉클

A(Shaded) 평면 접선은 미세하게 많은 입력 디스크, 출력 디스크 1개, 비 교차 문자열의 데이터로, 예를 들어 ${\displaystyle \mathrm{2n}}$ ${\displaystyle 2n$ 디스크당 간격 1개$,{\displaystyle }$ 디스크당 간격 ${\displaysty \star }$ -표시$$ 간격 1개.

여기서 마크는 $\star {\displaystyle }$ ${\displaystyle \star }$ - shape로$$ 표시된다.각 입력 디스크에서 그것은 두 개의 인접한 송신 문자열 사이에 배치되고 출력 디스크에서는 두 개의 인접한 수신 문자열 사이에 배치된다.평면 접선은 동위원소까지 정의된다.

구성

두 개의 평면 엉클을 구성하려면 한 평면의 출력 디스크를 다른 평면의 입력에 넣고, 표시된 간격의 음영과 동일한 음영으로 표시하며, $\star {\displaystyle }$ ${\displaystyle \star }$ -표시된$$ 간격이 일치하도록 한다.마침내 우리는 우연의 일치를 제거한다.두 개의 평면 접선은 0, 한 개 또는 여러 개의 가능한 구성을 가질 수 있다는 점에 유의하십시오.

플라나르 피연산자

평면 피연산자는 그러한 구성을 가진 모든 평면 접선(이형성까지의)의 집합이다.

플라나 대수

A planar algebra is a representation of the planar operad; more precisely, it is a family of vector spaces ${\displaystyle ({\mathcal {P}}_{n,\pm })_{n\in \mathbb {N} }}$, called ${\displaystyle n}$-box spaces, on which acts the planar operad, i.e. for any tangle ${\displaystyle T}$ (with one ou${\displaystyle {}_{}}$ ${\displaystyle {디스크}_{}}$와 $r{\displaystyle }$ ${\$ 및 ${\displaystyle {}_{}}$ 1 …, ${\displaystyle {2n}_{}}$ r ${\$n_${r$} 간격$$)에는$$ 멀티라인 맵이 있다.

${\displaystyle Z_{T}:{\mathcal {P}_{n_{1},\epsilon _{1}\otimes \cdots \otimes {\mathcal{P}_{n_{r},\epsilon _{r}}}\mathcal {P}{0},\epsilon _{0}}}}}}}}}}}}$

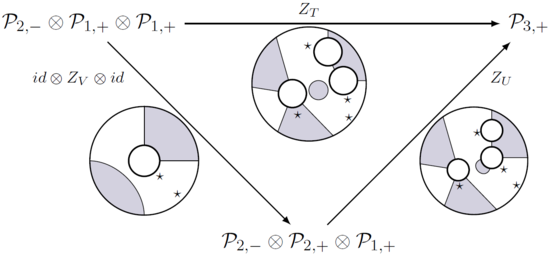
$ϵ{\displaystyle {}_{}}$ ${\displaystyle i_{}\in \{}$$$+ ,${\displaystyle }$- ${\displaystyle \}}$ ${\displaystyle \epsilon _{i}\in \{+,-\}}$의 음영에 따라$$ $displaysty \star }$ -표시된$$ 간격에 따라 \displaystone \-\}을 사용하여, 이러한 지도는 아래 모든 다이어그램이 통근하는 방식으로 접선 구성을 존중한다.

예

플라나르 뒤틀림

The family of vector spaces ${\displaystyle ({\mathcal {T}}_{n,\pm })_{n\in \mathbb {N} }}$ generated by the planar tangles having ${\displaystyle 2n}$ intervals on their output disk and a white (or black) ${\displaystyle \star }$-marked interval, admits a planar algebra structure.

템플리-리브

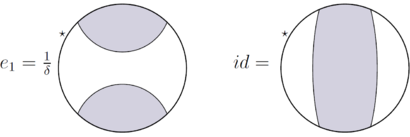
The Temperley-Lieb planar algebra ${\displaystyle {\mathcal {TL}}(\delta )}$ is generated by the planar tangles without input disk; its ${\displaystyle 3}$-box space ${\displaystyle {\mathcal {TL}}_{3,+}(\delta )}$ is generated by

또한 닫힌 문자열은 $\Delta {\displaystyle }$ ${\displaystyle \delta }$의 곱으로 대체된다$.$

$T{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle {\mathcal{L}}_{}}$ ${\displaystyle n_{}}$,${\displaystyle {}_{}}$±${\displaystyle {}_{}}$(${\displaystyle \Delta }$) ${\displaystyle {\mathcal {\tL}_{n},\pm }(\delta$)의 치수는 카탈로니아 번호 $1{\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{n}{}}$+ ${\displaystyle \frac{1}{}}$ ($){\${1$}{n+1}}{\binom {n}{n}}}}}}}}}}}}}}$이다$.$이 평면 대수학은 템플리-리브 대수학의 개념을 나타낸다.

호프 대수

대수적으로 폐쇄된 분야에 대한 반이행과 코세미이행 Hopf 대수학은 생성자와 관계에 의해 정의된 평면대수로 암호화되며, 0이 아닌 계량 ${\displaystyle \delta}}$와 깊이 2의 깊이와 연결된, 불가역, 구형, 비 퇴행성 평면대수에 대한 "상" (최대 이소모르핀)으로 암호화된다.^[7]

Note that connected means ${\displaystyle \dim({\mathcal {P}}_{0,\pm })=1}$ (as for evaluable below), irreducible means ${\displaystyle \dim({\mathcal {P}}_{1,+})=1}$, spherical is defined below, and non-degenerate means that the traces (defined below) are non-degenerate.

하위 인자 평면 대수

정의

하위 인자 평면 대수학(subfactor planar 대수학$)$은 평면${\displaystyle }$algebra{\$displaystyle \star }$ -algebra$$${\displaystyle }$(${\displaystyle {Pn}_{,}}$ ±${\displaystyle {}_{}{}_{}}$) ${\displaystyle n_{}}${ ${\displaystyle {N\mathbb{}}_{}}$ ${\$p}}}{\$mathcal{P},\pm}}_$${n\in \mathb{N}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.$

(1) 유한 치수: (Pn , ±)$<$ {\$displaystyle \dim({\mathcal{P}_${n,\pm$}}}}<\inflty }$

(2) 평가 대상:${\$

(3) 구형: $t{\displaystyle }$ ${\displaystyle r}$ ${\displaystyle :=}$ ${\displaystyle t}$ ${\displaystyle r_{}}$= ${\displaystyle t}$ ${\displaystyle {}_{}}$ ${\displaystyle l_{}}$ ${\$

(4) 양수: ⟨ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle ⟩}$= ${\displaystyle t}$ ${\displaystyle r}$(${\displaystyle {}^{}}$ ${\displaystyle {\star }^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle )}$ ${\displaystyle \langle a\vert b\rangle =tr(b^{\star }a)}$는 내부 제품을 정의한다$$.

(2) 및 (3)에 의해 닫힌 문자열(shaded 또는 not)은 동일한 상수 $\Delta {\displaystyle }$ ${\displaystyle \delta }$에 대해 계산된다는 점에 유의하십시오$.$

접선 작용은 다음과 같이 조정자를 다룬다.

${\displaystyle Z_{T}(a_{1}\otimes a_{2}\otimes \cdots \otimes a_{r}^{\star }}=Z_{T^{\star }}{{1}}^{{2}^{\star }\otimes \cdots \otimes a_{r}^{r}}{\star }}}}}$

with ${\displaystyle T^{\star }}$ the mirror image of ${\displaystyle T}$ and ${\displaystyle a_{i}^{\star }}$ the adjoint of ${\displaystyle a_{i}}$ in ${\displaystyle {\mathcal {P}}_{n_{i},\epsilon _{i}}}$.

예시 및 결과

No-host 정리:평면 대수 ${\displaystyle \mathcal{T}}$ L${\displaystyle }$(${\displaystyle \Delta }$) ${\displaystyle {\mathcal {TL}(\delta )}$에는 귀신이 없다$$(즉, 가 $원소{\displaystyle }$ a ${\displaystyle$ a$},$ 0인 경우 $\displaysty style$

${\displaystyle \in \{2\cos(\pi /n) n=3,4,5,...\}\컵 [2,+\큰 ]}$

위와 같은$$ $\Delta {\displaystyle }$ ${\displaystyle \delta}$의 경우 $I{\displaystyle \mathcal{}}$ ${\$을(를) null 이상( ideal${\displaystyle )}$으로 한다($$ (${\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle \langle a\langle =0}$을(를)으로 하는 $요소$에서 생성$).$Then the quotient ${\displaystyle {\mathcal {TL}}(\delta )/{\mathcal {I}}}$ is a subfactor planar algebra, called the Temperley–Lieb-Jones subfactor planar algebra ${\displaystyle {\mathcal {TLJ}}(\delta )}$. Any subfactor planar algebra with constant ${\displaystyle \delta }$ admits ${\displaystyle }$${\displaystyle \mathcal{T}}$ ${\displaystyle \mathcal{L}}$ ${\displaystyle \mathcal{J}}$ (${\displaystyle \Delta }$) ${\displaystyle {\mathcal {TLJ}(\delta )}$을(를) 평면 아발지브라(planar subalgebra)로$$ 표시한다.

A planar algebra ${\displaystyle ({\mathcal {P}}_{n,\pm })}$ is a subfactor planar algebra if and only if it is the standard invariant of an extremal subfactor ${\displaystyle N\subseteq M}$ of index ${\displaystyle [M:N]=\delta ^{2}}$, with ${\displaystyle {\mathcal{P}}_{n,+}=N^{\prime }\cap M_{n-1}}$${\displaystyle {\mathcal {P}}_{n,+}=N'\cap M_{n-1}}$ and ${\displaystyle {\mathcal {P}}_{n,-}=M'\cap M_{n}}$.^{[8] [9] [10]} A finite depth or irreducible subfactor is extremal (${\displaystyle tr_{N'}=tr_{M}}$ on ${\displaystyle N'\cap M}$).

유한한 그룹(그리고 보다 일반적으로는 유한 치수 $Hopf{\displaystyle {\mathrm{}}^{}}$ C${{\rm{C}^{\rm${C$}}}}}}}}}-$algebra$$, Kac 대수라고 함)를 부호화하는 하위 인자 평면 대수학이 있다.A (마인드 치수) Kac 대수학 "상응"(이형성까지)은 깊이 2의 불가해한 하위 인자 평면 대수학으로 한다.^{[11] [12]}

유한군 포함과 관련된 하위 인자 평면 대수로는 (핵심 없는) 포함을 항상 기억하지 못한다.^{[14] [15]}

A Bisch-Jones subfactor planar algebra ${\displaystyle {\mathcal {BJ}}(\delta _{1},\delta _{2})}$ (sometimes called Fuss-Catalan) is defined as for ${\displaystyle {\mathcal {TLJ}}(\delta )}$ but by allowing two colors of string with their own constant ${\displaystyle \delta _{$$1$.},$$ 2 {\$displaystyle \cHB _{$2}}, ${\displaystyle {위}_{}}$와 같이 $\Delta {\displaystyle {}_{}}$i {\$displaystyle \cHB_{i}}.$그것은 중간 계수를 가진 모든 하위 인자 평면 대수의 평면 하위 대수로서, $[{\displaystyle K}$: N ${\displaystyle ]}$= ${\displaystyle {}_{}^{}}$ ${\displaystyle {1\mathrm{}}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\$}}$$및$$${\displaystyle }$[${\displaystyle M}$: ${\displaystyle K}$ ${\displaystyle ]}$= ${\displaystyle {\Delta \mathrm{}}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\$

> 4 ${\displaystyle \delta ^{2}]4}$의 첫 번째 유한 깊이 하위 인자 평면 대수를 해거업 하위 인자 평면 대수라고 한다.^[18] ${\displaystyle 인덱스\mathrm{}}({\displaystyle 5}$+ ${\displaystyle \sqrt{13}}$)${\displaystyle }$/ 2${\displaystyle }$~ ${\displaystyle 4.303}$ ${\displaystyle(5+{\sqrt{13})/2\sim$ 4$.303}$을(를) 가지고 있다$.$

하위 인자 평면 알헤브라는 최대 $5{\displaystyle \mathrm{}}$ $[\displaystyle 5}$에서^[19] 약간 더 떨어진 곳에서 지수에 대해 완전히 분류된다.^[20] 이 분류는 우페 해거업에 의해 시작되었다.^[21] 그것은 내장 정리 및 해파리 알고리즘과 함께 가능한 주요 그래프의 목록을 사용한다.^[23]

하위 인자 평면 대수학에서는 보조 인자(즉, 표준 불변성이 완전함)를 준수할 수 있는 경우 이를 기억한다.^[24] 유한한 깊이 하이퍼피니트 하위요인은 수용 가능하다.

비-어메인 사례에 대하여: 모두 동일한 표준 불변성을 갖는 지수 6의 비분류성 하이퍼피니트 하위요소가 분류할 수 없이 많다.^[25]

푸리에 변환 및 2중 거부

$N{\displaystyle }$ ${\displaystyle \subset }$ ${\displaystyle M}$ ${\displaystyle N\subset M}$을(를) 유한 지수 하위 요인이 되게$$ 하고, $P{\displaystyle \mathcal{}}$ ${\${\$mathcal{P}$ 해당$$ 하위 인자 평면 대수인 것으로 한다.$P{\displaystyle \mathcal{}}$ ${\$이(가${\displaystyle {)}_{}}$ 복구할$$ 수 없는 상태라고 가정하십시오(${\displaystyle {예}_{\mathrm{}}}$: P${\displaystyle {}_{}}$1, + = ${\displaystyle {}^{}}$ ${\displaystyle \prime }$ ${\displaystyle {1\mathrm{}}_{}M\mathbb{}}$ 1 =$$C {\$displaystyle {\mathcal {P}}{1,+}=N'\cap M_{1}=\mathb {C}).$$N{\displaystyle }$ ${\displaystyle \subset }$ ${\displaystyle K}$ ${\displaystyle \subset }$ M ${\displaystyle N\subset K\subset M}$을(를) 중간 하위 요인이 되도록$$ 한다.Let the Jones projection ${\displaystyle e_{K}^{M}:L^{2}(M)\to L^{2}(K)}$. Note that ${\displaystyle e_{K}^{M}\in {\mathcal {P}}_{2,+}}$. Let ${\displaystyle id:=e_{M}^{M}}$ and ${\displaystyle e_{1}:=e_{N}^{M}$$}$.

$t{\displaystyle }$ ${\displaystyle r(}$ ${\displaystyle {e\mathrm{}}_{}}$ ${\displaystyle {}_{}}$)${\displaystyle }$= ${\displaystyle \Delta {}^{}}$- ${\displaystyle 2^{}}$=${\displaystyle }$[ ${\displaystyle {\mathrm{M}}^{}}$: N ${\displaystyle {}^{}}$- 1 ${\$ ${\displaystyle \mathrm{t<img\; alt="\{\backslash displaystyle\; tr(e\_\{1\})=\backslash delta\; ^\{-2\}=[M:N]^\{-1\}\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/9fd63195a24be73213cac05d2a89830dd84f65db"\; style="vertical-align:\; -0.838ex;\; width:25.488ex;\; height:3.176ex;"\; papago-attr-id="226">}(i}$ ${\displaystyle d}$ ${\displaystyle )}$= 1 ${\displaysty tr(id)=1$

Let the bijective linear map ${\displaystyle {\mathcal {F}}:{\mathcal {P}}_{2,\pm }\to {\mathcal {P}}_{2,\mp }}$ be the Fourier transform, also called ${\displaystyle 1}$-click (of the outer star) or ${\displaystyle 90^{\circ }}$ rotation; and let ${\displaystyle a*b}$$$ ${\displaystyle a}$ 및$$ $b{\displaystyle }$ ${\displaystyle b}$의 조합물이다$.$

코프로덕트라는 단어는 콘볼루션 제품의 축소판이라는 점에 유의하십시오.2진법이다.

duct${\displaystyle b}$= ${\displaystyle F\mathcal{}{}^{}}$(${\displaystyle F}$ -${\displaystyle {}^{}}$ ( ) F - ${\displaystyle 1^{}}$( ${\displaystyle b}$)${\displaystyle }$. ${\displaystyle a*b={\mathcal {{F}}({\mathcal {{F}}})(a){\mathcal{F}}^{-$1}^{-$1}(b$)를 만족한다$.$$}$

모든 양성 연산자 $a{\displaystyle }$, ${\displaystyle b}$ ${\displaystyle$ a$,b$의 경우,${\displaystyle b}$ b ${\displaystyle a*b}$도 양수이며$$, 이는 도식으로 볼 수 있다.

${\displaystyle :=F}$(${\displaystyle F}$($){\displaystyle{\overline{a}}:$$={\mathcal{F}({\mathcal{F})(a)}}$은(는$$) 역방향 a ${\$$displaystyle a}$이다($$${\displaystyle {180}^{}}$˚ $displaysty 180^{\circle }).$지도 $F{\displaystyle {\mathcal{}}^{}}$ ${\$는 외부 별의 네 $개$의 1 ${\displaystyle 1}$클릭에$$ 해당하므로$$, ID 맵이고, 그 다음 }'은${\displaystyle (}$는) ${\displaystyle {\overline{a}=a}}$에 해당된다$.$

Kac 대수학 사례에서 역행은 정확히 대척점이며,^[12] 유한 집단의 경우 역행과 일치한다.

biprojection은 투영 $b{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle {\mathcal{}}_{}}$ ${\displaystyle 2_{\mathrm{}}}$$$,${\displaystyle {}_{}}$+ ${\displaystyle {}_{}}${ ${\displaystyle 0\}}$ ${\displaystyle b\in {\p}_{2,+}\setminus \{0\}}}$을(를$)$ $가진$ 투영 b ($)$이며$,$ 투영 배수는 F $b$)이다$.$$e{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$= ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$ M ${\$ 및$$ $i{\displaystyle d}$ = ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}${\$displaystyle id=e_{M}^{M}}}}}$은(는) 2중 거부이므로$$ 다음과 같이 볼 수 있다.

투영 b{\displaystyle b}은 biprojection iff의 KM{\displaystyle e_{K}^{M}e 중간subfactor N⊂ K⊂ M{N\subset K\subset M\displaystyle}[27]의 존스 프로젝션},iff e1≤ b)b¯=λ −과λ b∗ b, 1)δ tr(b){\displaystyle e_{1}\leq b={\overline{b}}=\la.mbda$b*b,{\text{{}\}\boda ^{-1}=\b(b$ .

갈루아 대응: Kac 대수학 사례에서, 두피거부는 왼쪽 코이데탈 아발게브라와 1-1이며, 유한집단의 경우 하위집단에 해당한다.

모든 불가해한 하위 인자 평면 대수에서, 2중 불합격의 집합은 유한 집단의${\displaystyle }$간격에 대해${\displaystyle }$[${\displaystyle e}$ ${\displaystyle 1}$,${\displaystyle {}_{}i}$] ${\displaystyle [e_{1$}id$]\}$ 형식인 [H, ${\displaystyle G}$]${\displaystyle [H,G]}$의 유한 격자 형식이다$.$

바이프로스를 이용하여 중간 소인수 평면 알헤브라를 만들 수 있다.^{[31] [32]}

불확도 원리는 수정 불가능한 하위 인자 평면 대수 $P{\displaystyle \mathcal{}}$ ${\$까지 확장된다$.$

Let ${\displaystyle {\mathcal {S}}(x)=Tr(R(x))}$ with ${\displaystyle R(x)}$ the range projection of ${\displaystyle x}$ and ${\displaystyle Tr}$ the unnormalized trace (i.e. ${\displaystyle Tr=\delta ^{n}tr}$ on ${\displaystyle {\mathc$$al{P}_{n,\pm }}.$

비확실성 원칙:^[33] $x{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle {\mathcal{}}_{}}$ ${\displaystyle 2_{\mathrm{}}}$,${\displaystyle {}_{}}$± ${\$ $\}\}$을(를) 0이 아닌 상태로 두십시오.그러면

${\displaystyle {\mathcal {S}(x){\mathcal {S}({\mathcal {F}(x))\geq \delta ^{2}}$

$x{\displaystyle }$ ${\displaystyle x}$ 및$$ $F{\displaystyle \mathcal{}(x}$ ${\displaystyle )}$ ${\displaystyle {\mathcal {F}(x)}$이(가) 양수라고 가정하면, $x{\displaystyle }$ ${\displaystyle x}$이(가) 양수인 경우에만 동등성이 유지된다.더 일반적으로, 평등은 만약 $x{\displaystyle }$ ${\displaystyle x}$이(가) 바이프로주사의 양방향일 경우에만 유지된다.

참조