존스 다항식
Jones polynomial매듭 이론의 수학적 분야에서 존스 다항식은 1984년 본 존스가 발견한 매듭 다항식이다.[1][2]구체적으로는 각 방향 매듭에 할당하거나 / 22}}의 Laurent 다항식을 정수 계수로 연결하는 방향 매듭 또는 링크의 불변성이다.[3]null
브래킷별 정의
매듭 다이어그램으로 제공된 방향 링크 이(가) 있다고 가정해 보십시오우리는 우리가 로 나타내는 루이까우프만의 브래킷 다항식을 사용하여존스 다항식 V ( 을 정의할 것이다 여기서 브래킷 다항식은 정수 계수를 가진 A 변수에서 Laurent 다항식이다.null
먼저 보조 다항식(평준화된 브래킷 다항식이라고도 함)을 정의한다.
여기서 ( ) 은(는) 다이어그램에서 L {\의 쓰기를 나타낸다.다이어그램의 쓰기는 양의 교차 횟수( 그림의 L+ 에서 음의 교차 횟수(- 를 뺀 값이다.그 글은 매듭에 불변하는 것이 아니다.null
( ) 은(는) 세 개의 레이디마이스터 움직임에 L L의 도표 변경에 따라 불변하므로 매듭 불변형이다.타입 II 및 III 레이디메이스터 이동에 따른 비침습은 그러한 이동에 따른 브래킷의 비침습에서 따른다.브래킷 다항식은 타입 I 레이데마이스터 이동 -A ± 3의 인수에 의해 변경되는 것으로 알려져 있다.에 주어진 다항식의 정의는 I 타입 이동 시 +1 1또는- 1 에 의해 적절히 쓰기 작업이 변경되기 때문에 이 변경을 무효화하도록 설계되었다.null
Now make the substitution in to get the Jones polynomial . This results in a Laurent polynomial with integer coefficients in the variable .
접기용 존스 다항식
이 접선용 존스 다항식 구조는 링크의 카우프만 브라켓을 단순 일반화한 것이다.이 공사는 블라디미르 투레프가 개발하여 1990년에 간행하였다.[4]null
을(를) 음이 아닌 정수로 하고 k 는 {\ 끝의 모든 동위원소 유형의 접선도를 나타내며 교차점이 없고 닫힌 구성 요소(스무팅)가 없다.Turaev's construction makes use of the previous construction for the Kauffman bracket and associates to each -end oriented tangle an element of the free -module , where is the ri변수 / 에 정수 계수가 있는 Laurent 다항식의 ng
브레이드 표현에 의한 정의
존스가 다항식을 처음 공식화한 것은 연산자 알제브라를 연구한 데서 비롯되었다.존스의 접근 방식에서, 그것은 통계 역학에서 포츠 모델과 같은 특정 모델을 연구하면서 원래부터 생겨난 대수학으로 특정 땋은 표현에 대한 일종의 "추적"에서 비롯되었다.null
링크 L을 제공하라.알렉산더의 정리는 그것이 n 가닥으로 말하자면 땋은 자리의 흔적 폐쇄라고 말한다.Now define a representation of the braid group on n strands, Bn, into the Temperley–Lieb algebra with coefficients in and . 표준 브레이드 생성기 i 는 + - 로 전송된다. 여기서 , e, e , e - 1 1는 템플리-리브 대수학의 표준 생성기다.이것이 표현을 정의한다는 것을 쉽게 확인할 수 있다.null
이전에 에서 얻은 브레이드 단어 을(를) 선택하고 {를 계산하십시오. 여기서tr은 displaystytrace이렇게 하면 이(가) 제공되며 여기서 은(는) 브래킷 다항식이다.이것은 루이 카우프만이 그랬던 것처럼 템플리-리브 대수학을 특정 다이어그램 대수로서 고려함으로써 알 수 있다.null
이 접근방식의 장점은 R-매트릭스 표현과 같은 다른 알헤브라와 유사한 표현을 선택하여 "일반화된 존스 불변제"로 이어질 수 있다는 것이다.null
특성.
존스 다항식(Jones polyomial)은 어떤 도표에서든 1 값을 취하며 다음과 같은 스키닌 관계를 만족하는 것이 특징이다.
여기서 + L- 은 아래 그림에 표시된 교차 변경이나 스무딩에 의해 다른 하나의 작은 영역을 제외하고 동일한 세 가지 방향의 링크 다이어그램이다.
브래킷에 의한 Jones 다항식의 정의는 K{\K에 대해 ( K) 1}의t- 1 {\ t^{-을 대체하여 해당 미러 이미지의 Jones 다항식이 제공됨을 쉽게 보여줄 수 있다따라서, 그것의 거울 이미지와 동등한 매듭인 암피시알 매듭은 그것의 다항식에 팔린드로믹 엔트리를 가지고 있다.이러한 관계를 사용하는 계산의 예는 스키인 관계에 대한 기사를 참조하십시오.null
이 불변성의 또 다른 주목할 만한 속성은 교번 링크의 존스 다항식이 교번 다항식이라는 것을 말한다.이 재산은 1987년 Morwen Thisttwaite에[5] 의해 증명되었다.이 마지막 재산에 대한 또 다른 증거는 헤르난도 부르고스 소토(Hernando Burgos-Soto) 때문인데, 그는 또한 그 재산의 뒤엉킨[6] 부분에 대해서도 연장을 해주었다.null
컬러 존스 다항식
양의 정수 의 경우 - 컬러 Jones 다항식 t) 은 존스 다항식의 일반화다.레셰티킨-이다.Turaev invariant associated with the -irreducible representation of the quantum group . In this scheme, the Jones polynomial is the 1-colored Jones polynomial, the Reshetikhin-Turaev invariant associated to the standard representation(불확실성 및 2차원) ( l2 2 링크의 가닥을 표현에 의해 "색"이라고 생각하므로 이름이 붙는다.null
More generally, given a link of components and representations of , the -colored Jones 다항식 V ,…, k( , ) 은 레셰티킨–이다. ,…, 과(여기서 구성품이 주문되었다고 가정함). 및 W 두 가지 표현을 사용할 경우 색상이 지정된 Jones 다항식은 다음 두 가지 속성을 충족한다[7]
- ⊕ (L ,) = V( L, )+ W( , ) ,
- , where denotes the 2-cabling of .
이러한 성질은 색깔 있는 존스 다항식이 레셰티킨-투레프 불변제라는 사실에서 추론된다.null
을(를) 매듭짓게 하라.Kauffman 브라켓 덕분에 Thermley-Lieb 대수학의 로서 K 의 도표를 K K}의 존스 다항식 다항식을 복구한다는 사실을 상기하십시오 로 K 의 N - 컬러 다항목을 조합하여 설명할 수 있다.ng Jones-Wenzl idempotents 다음과 같다.
- 의 displaystyle } K을(를) 고려하십시오
- 템플리-리브 대수학의 한 요소로 간주한다.
- N {\ 평행 가닥에 Jones-Wenzl idempotents를 삽입한다
( ) 의 결과 요소는 - 컬러 Jones 다항식이다.자세한 내용은 의 부록 H를 참조하십시오.null
다른 이론과의 관계
체르-시몬스 이론과 연계
으로서 먼저 에드워드 Witten,[9] 주어진 매듭 γ{\displaystyle \gamma}의 존스 다항식은three-sphere에 게이지 그룹 SU(2){\displaystyle \mathrm{SU}(2)}을 사용하여 윌슨 고리 WF(γ){\displaystyle W_{F}의 진공 기대 값을 계산할 Chern–Simons 이론을 고려하여 얻을 수 있다.(\g {\과와 관련된과와) S U( )의 표현 F {\ F과와 {\
양자 매듭 불변성과의 연결
e 를 존스 다항식의 t 에 대체하고 이를 일련의 h로 확장하여 매듭 의 바실리예프 불변량(또는 유한형 불변량을 통일하기 위해 막심 콘체비치.콘체비치 적분을 건설했다.자코비 코드 다이어그램으로 명명된 1, 3값 화음 다이어그램의 무한 합인 콘체비치 적분 값은 Dror Bar-Natan이 연구한 l }} 중량 시스템과 함께 존스 다항식을 재현한다.null
볼륨 추측과 연결
리나트 카샤에프는 일부 쌍곡 매듭에 대한 수학적 조사를 통해 단결의 n번째 뿌리를 n차원 표현에 해당하는 색색의 존스 다항식의 매개변수로 대체하고, n이 무한대로 성장함에 따라 제한 값을 지정하면 매듭의 쌍곡 볼륨을 보완할 수 있다는 것을 발견했다.(볼륨 콘제 참조)cture)
호바노프 호몰로지와의 연계
2000년에 미하일 코바노프는 매듭과 고리를 위한 특정한 체인 콤플렉스를 건설했고 그것으로부터 유도된 호몰로지(homology)가 매듭 불변성임을 보여주었다(Kovanov homology 참조).Jones 다항식은 이 호몰로학의 오일러 특성으로 설명된다.null
문제 열기
- 존스의 다항식과의 비종교적인 매듭이 언노트의 매듭과 동일한가?Morwen Thisttwaite의 작업에 의한 해당 언링크와 동등한 존스의 다항식과의 비종교적 연계가 있는 것으로 알려져 있다.
- 문제성존스 다항식의 일반 3-매니폴드로의 확장
"원래 존스 다항식은 3-sphere의 1-링크(3-볼, 3-공간 3 에 대해 정의되었다.3-매니폴드의 1-링크에 대한 존스 다항식을 정의할 수 있는가?'
그러한 접근법은 Skin 모듈이라는 이름으로 Jozef H. Przytycki에 의해 제안되었다.특히 카우프만 브래킷 스키인 모듈과 HOMFLYPT 스키인 모듈.[10]null
이 문제의 배경과 내역은 이 문서의[11] 1.1절을 참조하십시오.카우프만은 폐쇄 지향 표면의 제품 다지관과 폐쇄 간격의 경우 가상 1코트를 도입해 솔루션을 제출했다.[12]그것은 다른 경우에는 열려 있다.존스 다항식 링크가 통합된 비튼의 경로는 어떤 콤팩트한 3-매니폴드의 링크에 대해서도 정식으로 작성되지만, 미적분은 3-sphere(3-ball 또는 3-space R 이외의 경우에도 물리학 수준에서도 수행되지 않는다.이 문제는 물리학 수준에서도 열려 있다.알렉산더 다항식의 경우 이 문제가 해결된다.null
참고 항목
메모들
- ^ Jones, Vaughan F.R. (1985). "A polynomial invariant for knots via von Neumann algebra". Bulletin of the American Mathematical Society. (N.S.). 12: 103–111. doi:10.1090/s0273-0979-1985-15304-2. MR 0766964.
- ^ Jones, Vaughan F.R. (1987). "Hecke algebra representations of braid groups and link polynomials". Annals of Mathematics. (2). 126 (2): 335–388. doi:10.2307/1971403. JSTOR 1971403. MR 0908150.
- ^ "Jones Polynomials, Volume and Essential Knot Surfaces: A Survey" (PDF).
- ^ Turaev, Vladimir G. (1990). "Jones-type invariants of tangles". Journal of Mathematical Sciences. 52: 2806–2807. doi:10.1007/bf01099242. S2CID 121865582.
- ^ Thistlethwaite, Morwen B. (1987). "A spanning tree expansion of the Jones polynomial". Topology. 26 (3): 297–309. doi:10.1016/0040-9383(87)90003-6.
- ^ Burgos-Soto, Hernando (2010). "The Jones polynomial and the planar algebra of alternating links". Journal of Knot Theory and Its Ramifications. 19 (11): 1487–1505. arXiv:0807.2600. doi:10.1142/s0218216510008510. S2CID 13993750.
- ^ Gukov, Sergei; Saberi, Ingmar (2014). "Lectures on Knot Homology and Quantum Curves". Topology and Field Theories. Contemporary Mathematics. Vol. 613. pp. 41–78. arXiv:1211.6075. doi:10.1090/conm/613/12235. ISBN 9781470410155. S2CID 27676682.
- ^ 오쓰키, 양자 불변제: 매듭, 3마니폴드, 그리고 그 집합에 관한 연구
- ^ Witten, Edward (1989). "Quantum Field Theory and the Jones Polynomial" (PDF). Communications in Mathematical Physics. 121 (3): 351–399. Bibcode:1989CMaPh.121..351W. doi:10.1007/BF01217730. S2CID 14951363.
- ^ Przytycki, Józef H. (1991), "Skein modules of 3-manifolds", Bulletin of the Polish Academy of Sciences, 39 (1–2): 91–100, arXiv:math/0611797
- ^ Kauffman, Louis H.; Ogasa, Eiji; Schneider, Jonathan (2018), A spinning construction for virtual 1-knots and 2-knots, and the fiberwise and welded equivalence of virtual 1-knots, arXiv:1808.03023
- ^ Kauffman, L.E. (1998), Talks at MSRI Meeting in January 1997, AMS Meeting at University of Maryland, College Park in March 1997, Isaac Newton Institute Lecture in November 1997, Knots in Hellas Meeting in Delphi, Greece in July 1998, APCTP-NANKAI Symposium on Yang-Baxter Systems, Non-Linear Models and Applications at Seoul, Korea in October 1998, Virtual knot theory, European J. Combin. 20 (1999) 663-690, arXiv:math/9811028
참조
- Adams, Colin (2000-12-06). The Knot Book. American Mathematical Society. ISBN 0-8050-7380-9.
- Jones, Vaughan. "The Jones Polynomial" (PDF).
- Jones, Vaughan (1987). "Hecke algebra representations of braid groups and link polynomials". Annals of Mathematics. 126 (2): 335–388. doi:10.2307/1971403. JSTOR 1971403.
- Kauffman, Louis H. (1987). "State models and the Jones polynomial". Topology. 26 (3): 395–407. doi:10.1016/0040-9383(87)90009-7. (대괄호 다항식별 정의 및 땋은 표현에 의한 Jones의 공식과 관련성 설명)
- Lickorish, W. B. Raymond (1997). An introduction to knot theory. New York; Berlin; Heidelberg; Barcelona; Budapest; Hong Kong; London; Milan; Paris; Santa Clara; Singapore; Tokyo: Springer. p. 175. ISBN 978-0-387-98254-0.
- Thistlethwaite, Morwen (2001). "Links with trivial Jones polynomial". Journal of Knot Theory and Its Ramifications. 10 (4): 641–643. doi:10.1142/S0218216501001050.
- Eliahou, Shalom; Kauffman, Louis H.; Thistlethwaite, Morwen B. (2003). "Infinite families of links with trivial Jones polynomial". Topology. 42 (1): 155–169. doi:10.1016/S0040-9383(02)00012-5.
- Przytycki, Józef H. (1991). "Skein modules of 3-manifolds". Bulletin of the Polish Academy of Sciences. 39 (1–2): 91–100. arXiv:math/0611797.
외부 링크
- "Jones-Conway polynomial", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Morwen Thisttwaite의 Jones 다항식 링크
- "The Jones Polyomial"(존스 다항식) 'The Noth Atlas.

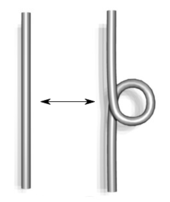


















![\mathrm{R}[S_k]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0317a361840afc9f107aa41811d61e79572eedf)


![{\displaystyle \mathbb {Z} [A,A^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/471c9cc58033dff68253c7995a3cb3c9753af5f1)



 템플리-리브 대수학의 표준 생성기다.이것이 표현을 정의한다는 것을 쉽게 확인할 수 있다.null
템플리-리브 대수학의 표준 생성기다.이것이 표현을 정의한다는 것을 쉽게 확인할 수 있다.null
 계산하십시오. 여기서
계산하십시오. 여기서


 (는) 브래킷 다항식이다.이것은
(는) 브래킷 다항식이다.이것은 




 대체하여 해당 미러 이미지의 Jones 다항식이 제공됨을 쉽게 보여줄 수 있다
대체하여 해당 미러 이미지의 Jones 다항식이 제공됨을 쉽게 보여줄 수 있다


















 대체하고 이를 일련의 h로 확장하여 매듭
대체하고 이를 일련의 h로 확장하여 매듭 


