다각형 사슬

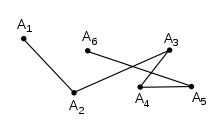
Polygonal chain
단순한 폴리곤 체인
자체 교차 폴리곤 체인
닫힌 다각형 체인

기하학에서 다각형 체인은 연결된 일련의 선분입니다.좀 더 형식적으로 다각형 PP는 정점이라고 일련의점 A2 …,에 의해 지정된 곡선입니다.곡선 자체는 연속된 정점을 연결하는 선 세그먼트로 구성됩니다.

이름.

다각형 사슬은 다각형 곡선,[1] 다각형 경로,[2] 폴리선,[3] 부분 선형 곡선,[3] 파선[4], 또는 지리 정보 시스템에서는 라인스트링 또는 선형 [5]링이라고도 할 수 있다.

바리에이션

단순 폴리곤 체인은 연속된 세그먼트(또는 처음과 마지막)만 해당 끝점에서 교차하는 체인입니다.

닫힌 다각형 사슬은 첫 번째 정점이 마지막 정점과 일치하거나 또는 첫 번째 정점과 마지막 정점이 [6]선분으로 연결된 사슬이다.평면에서 단순 닫힌 폴리곤 체인은 단순 폴리곤의 경계입니다.종종 "폴리곤"이라는 용어는 "닫힌 다각형 체인"의 의미로 사용되지만, 경우에 따라 다각형 영역과 다각형 체인 간에 구분을 그리는 것이 중요합니다.

다각형 체인은 L에 수직인 모든 선이 한 번에 체인과 교차하도록 직선 L이 있는 경우 모노톤이라고 합니다.모든 사소한 단조 다각형 사슬이 열려 있습니다.이에 비해 모노톤 폴리곤은 정확히 두 개의 모노톤 [7]체인으로 분할할 수 있는 폴리곤(폐쇄 체인)입니다.부분 선형 함수의 그래프는 수평선에 대해 단조로운 사슬을 형성합니다.

n=17개의 점 집합은 4개의 동일한 부호 기울기를 가진 다각형 경로를 가진다.

특성.

n개 의{\ n개 이상의 포인트 세트에는 모든 슬로프가 동일한 기호를 갖는 최소n - { 개의 다각형 경로가 포함됩니다.이것은 Erdss-Szekeres 정리의 결과이다.

적용들

폴리곤 체인은 종종 보다 복잡한 곡선을 근사하는 데 사용될 수 있습니다.이 맥락에서 라메르-더글라스-피커 알고리즘을 사용하여 정확한 [8][9]근사치 역할을 하는 세그먼트가 적은 다각형 체인을 찾을 수 있습니다.

그래프 그리기에서는 모서리를 직선 세그먼트로 그리면 교차, 모서리-버텍스 충돌 또는 기타 바람직하지 않은 피쳐가 발생하는 그리기 스타일에서 다각형 체인이 그래프의 모서리를 나타내는 데 자주 사용됩니다.이러한 맥락에서 도면의 시각적 혼란을 줄이기 위해 가능한 한 적은 세그먼트와 벤드로 모서리를 그리는 것이 좋습니다. 벤딩 수를 최소화하는 문제를 벤딩 [10]최소화라고 합니다.

폴리곤 체인은 컴퓨터 지오메트리의 기본 데이터 유형이기도 합니다.예를 들어 Lee와 Preparata의 점 위치 알고리즘은 임의의 평면 분할을 2진수 검색으로 해결할 수 있는 단조 사슬의 순서 있는 시퀀스로 분해함으로써 동작한다.이 방법은 나중에 점 위치 [11]문제에 대해 최적의 시간 경계를 제공하도록 개량되었다.

지리정보시스템에서, 라인링은 어떤 선형 지오메트리를 나타낼 수 있으며, 잘 알려진 텍스트 마크업을 사용하여 설명될 수 있습니다.LineString또는MultiLineString.[5] 리니어 링(또는LinearRing)는 폴리곤 지오메트리를 작성하는 데 사용되는 닫힌 폴리곤 체인입니다.

「 」를 참조해 주세요.

  • 체인(대칭 위상), 1차원의 경우 다각형 체인을 포함하는 단순성의 형식 조합
  • 복합 베지어 곡선, 폴리곤 체인의 각 직선을 매끄러운 곡선으로 대체하는 일반화입니다.
  • 연결 거리, 폴리곤 내에서 두 점을 연결하는 최단 체인의 세그먼트 수
  • 부분 회귀
  • 추상 그래프의 유사한 개념인 경로(그래프 이론)
  • 단조로운 폴리곤 체인의 3D 일반화인 다면체 지형
  • 나선형 다각형 사슬인 나선형
  • 매듭을 닫힌 다각형 체인으로 나타내는 데 기반하는 매듭 불변량인 스틱 번호
  • 다각측량, 측량 시 적용

레퍼런스

  1. ^ 를 클릭합니다Gomes, Jonas; Velho, Luiz; Costa Sousa, Mario (2012), Computer Graphics: Theory and Practice, CRC Press, p. 186, ISBN 9781568815800.
  2. ^ 를 클릭합니다Cheney, Ward (2001), Analysis for Applied Mathematics, Graduate Texts in Mathematics, vol. 208, Springer, p. 13, ISBN 9780387952796.
  3. ^ a b 를 클릭합니다Boissonnat, Jean-Daniel; Teillaud, Monique (2006), Effective Computational Geometry for Curves and Surfaces, Springer, p. 34, ISBN 9783540332596.
  4. ^ Muggeo, Vito M. R. (May 2008), "segmented: An R package to fit regression models with broken-line relationships" (PDF), R News, 8 (1): 20–25
  5. ^ a b Open Geospatial Consortium (2011-05-28), Herring, John R. (ed.), OpenGIS® Implementation Standard for Geographic information - Simple feature access - Part 1: Common architecture, 1.2.1, Open Geospatial Consortium, retrieved 2016-01-15
  6. ^ 를 클릭합니다Mehlhorn, Kurt; Näher, Stefan (1999), LEDA: A Platform for Combinatorial and Geometric Computing, Cambridge University Press, p. 758, ISBN 9780521563291.
  7. ^ 를 클릭합니다O'Rourke, Joseph (1998), Computational Geometry in C, Cambridge Tracts in Theoretical Computer Science, Cambridge University Press, p. 45, ISBN 9780521649766.
  8. ^ 를 클릭합니다Ramer, Urs (1972), "An iterative procedure for the polygonal approximation of plane curves", Computer Graphics and Image Processing, 1 (3): 244–256, doi:10.1016/S0146-664X(72)80017-0.
  9. ^ 를 클릭합니다Douglas, David; Peucker, Thomas (1973), "Algorithms for the reduction of the number of points required to represent a digitized line or its caricature", The Canadian Cartographer, 10 (2): 112–122, doi:10.3138/FM57-6770-U75U-7727.
  10. ^ 를 클릭합니다Tamassia, Roberto (1987), "On embedding a graph in the grid with the minimum number of bends", SIAM Journal on Computing, 16 (3): 421–444, doi:10.1137/0216030.
  11. ^ 를 클릭합니다Edelsbrunner, Herbert; Guibas, Leonidas J.; Stolfi, Jorge (1986), "Optimal point location in a monotone subdivision", SIAM Journal on Computing, 15 (2): 317–340, doi:10.1137/0215023.