쿼츠 크리스털 마이크로밸런스

쿼츠 결정 마이크로 밸런스(QCM)(쿼츠 마이크로 밸런스(QMB)라고도 하며, 쿼츠 결정 나노밸런스(QCN)라고도 함)는 쿼츠 결정 공명기의 주파수 변화를 측정하여 단위 면적당 질량 변동을 측정한다. 공명은 음향 공명기의 표면에 산화물 성장/디케이 또는 필름 침적으로 인해 작은 질량의 추가 또는 제거에 의해 방해된다. QCM은 진공 상태, 가스 단계("가스 센서", King에서^[1] 처음 사용)에서 그리고 최근에는 액체 환경에서 사용될 수 있다. 진공 상태에서 박막 증착 시스템의 증착 속도를 모니터링하는 데 유용하다. 액체에서는 인식 부위로 기능화된 표면에 대한 분자(특히 단백질)의 친화력을 결정하는 데 매우 효과적이다. 바이러스나 폴리머와 같은 더 큰 실체도 조사된다. QCM은 또한 생체 분자 간의 상호작용을 조사하는데 사용되었다. 주파수 측정은 고정밀(아래 설명)으로 쉽게 이루어지기 때문에 1μg/cm² 이하의 수준으로 질량 밀도를 측정하는 것이 용이하다. 주파수 측정에 더하여, 분산 계수(공명 대역폭과 동일)를 종종 측정하여 분석을 돕는다. 소산 인자는⁻¹ 공명의 역품질 인자 Q = w/f_r(아래 참조)로, 시스템의 감쇠도를 정량화하며 표본의 점탄성 특성과 관련이 있다.

일반

Quartz는 압전 효과를 경험하는 결정체 계열의 한 구성원이다. 압전 효과는 고출력, 센서, 액추에이터, 주파수 표준, 모터 등에서 응용 프로그램을 발견했으며, 인가 전압과 기계적 변형 사이의 관계는 잘 알려져 있다. 이는 전기적 수단으로 음향 공진을 프로빙할 수 있다. 쿼츠 크리스탈에 교류를 적용하면 진동이 유발된다. 적절하게 절단된 결정의 전극 사이에 교류와 함께 스탠딩 전단파가 발생한다. 주파수와 대역폭의 비율인 Q 계수는 10까지⁶ 올라갈 수 있다. 이렇게 좁은 공명은 매우 안정된 발진기와 공진 주파수의 결정에 높은 정확도로 이어진다. QCM은 이러한 용이성과 정밀성을 이용하여 감지한다. 공통 장비는 4~6MHz 범위에서 기본 공명 주파수를 가진 결정에서 1Hz까지 분해능을 낮출 수 있다. QCM의 일반적인 설정에는 수냉관, 리테이닝 장치, 마이크로닷 피드쓰루를 통한 주파수 감지 장비, 진동원, 측정 및 기록 장치가 포함된다.

석영 결정의 진동 빈도는 결정의 두께에 따라 부분적으로 좌우된다. 정상 작동 중에는 다른 모든 영향 변수가 일정하게 유지되므로 두께 변화는 주파수의 변화와 직접적인 상관관계가 있다. 질량이 결정 표면에 축적되면 두께가 증가하며, 결과적으로 초기 값보다 진동 빈도가 감소한다. 몇 가지 간단한 가정으로, 이러한 주파수 변화는 Sauerbrey 방정식을 사용하여 질량 변화에 정확하게 계량되고 상관될 수 있다.^[2] 박막의 특성을 측정하는 다른 기법으로는 타원측정법, 표면 플라스몬 공명(SPR) 분광법, 다중 파라미터 표면 플라스몬 공명법 및 이중 편광 간섭법 등이 있다.

중력 및 비중력 QCM

쿼츠 크리스탈 공명기의 고전적 감지 적용은 마이크로중력측정법이다.^{[3][4][5][6][7][8]} 두께 모니터라고 불리는 많은 상업용 계기들이 이용 가능하다. 이 장치들은 사우어브레이 관계를 이용한다.^[2] 박막의 경우 공명 주파수는 보통 판의 총 두께에 반비례한다. 후자는 필름이 수정 표면에 침전될 때 증가한다. 모노레이어 감도는 쉽게 도달할 수 있다. 그러나 필름 두께가 증가하면 점탄성 효과가 발휘된다.^[9] 1980년대 후반에는 대형 댐핑의 결과를 극복하기 위한 적절한 조치가 취해진다면 QCM도 액체로 작동할 수 있다는 점을 인식했다.^[10][11] 다시 말하지만, 점탄성 효과는 공진 특성에 강하게 기여한다.

오늘날 마이크로웨이잉은 QCM의 여러 용도 중 하나이다.^[12] 점도와 보다 일반적인 점성, 점성 성질의 측정도 매우 중요하다. "비중력" QCM은 결코 기존의 QCM의 대안이 아니다. 중력 측정 이외의 목적으로 석영 공진기를 사용하는 많은 연구자들은 석영 결정 공진기를 QCM이라고 계속 불러왔다.사실 '균형'이라는 용어는 힘의 균형이라는 의미에서 이해된다면 무중력 적용에도 일리가 있다. 공진에서 표본에 의해 결정체에 가해지는 힘은 결정 내부의 전단 경사도에서 발생하는 힘에 의해 균형을 이룬다. 이것이 소하중 근사치의 본질이다.

QCM은 관성 질량을 측정하며, 따라서 높은 공진 주파수로 작동함으로써 재료가 표면에 추가(또는 제거)될 때 관성의 작은 변화에 매우 민감하게 만들 수 있다. 그에 비해 중력 질량 측정의 민감도는 지구의 중력장 강도에 의해 제한된다. 우리는 보통 균형을 중력 질량을 측정하는 방법이라고 생각하는데, 이는 지구가 무게를 재는 신체에 가하는 힘에 의해 측정된다. 몇 가지 실험에서는 추적 가능한(중력 질량) 중량과 QCM 측정값을 비교하여 QCM과 SI 시스템 사이의 직접적인 연관성을 입증했다.^[13]

결정 α–쿼츠는 두께-바닥 공진기에 있어 단연 가장 중요한 물질이다. 랑가사이트(LaGaSiO₃₅₁₄, "LGS")와 갈륨-정인산염(GaPO₄)은 주로 고온에서 사용하기 위해 석영에 대한 대안으로 조사된다.^[14][15] 이러한 장치는 석영으로 만들어지지 않았음에도 불구하고(그리고 중력 측정에는 사용될 수도, 사용하지 않을 수도 있다) "QCM"이라고도 불린다.

표면 음향파 기반 센서

QCM은 표면의 음향파를 기반으로 한 광범위한 종류의 감지 기구의 구성품이다. 유사한 작동 원리를 공유하는 계측기는 전단 수평 표면 음향파(SH-SW) 장치,^[16][17] 사랑파 장치^[18] 및 비틀림 공명기 등이다.^[19][20] 표면 음향파 기반 장치는 결정 표면에서 음향파의 반사율이 인접 매체의 임피던스(응력 대 속도 비율)에 따라 달라진다는 사실을 이용한다. (온도나 압력에 대한 일부 음향센서는 결정 내부의 음속은 온도, 압력 또는 휨에 따라 결정된다는 사실을 이용한다. 이러한 센서는 표면 효과를 이용하지 않는다.) 표면-음향파 기반 감지라는 맥락에서 QCM은 "풍선 음향파 공명기(BAW-리소네이터)" 또는 "두경-표면 공명기"라고도 불린다. 비적재 BAW 공명기의 변위 패턴은 결정 표면에 안티노드가 있는 스탠딩 전단파다. 이것은 분석을 특히 쉽고 투명하게 만든다.

기악기

공명 결정체

QCM이 처음 개발되었을 때 천연 석영을 채취하여 품질에 따라 선별한 후 실험실에서 절단하였다. 그러나 오늘날 대부분의 결정체들은 씨앗 결정체를 사용하여 재배된다. 씨앗 결정체는 결정 성장을 위한 고정점과 템플릿의 역할을 한다. 성장한 크리스털은 이후 1~30MHz 범위에서 두께 전단 공진을 지원하는 얇은 모발 디스크로 자르고 다듬는다. 응용 프로그램에서는 "AT" 또는 "SC" 지향 컷(아래 설명)이 널리 사용된다.^[21]

전기기계 커플링

QCM은 양쪽에 전극이 증발된 얇은 압전판으로 구성된다. 피에조 효과로 인해 전극을 가로지르는 AC 전압은 전단 변형을 유도하며, 그 반대의 경우도 마찬가지다. 전자기계 결합은 전기적 수단으로 음향 공진을 감지하는 간단한 방법을 제공한다. 그렇지 않으면 그것은 중요하지 않다. 그러나 전자기계 커플링은 압전 경화를 통해 공명 주파수에 약간의 영향을 미칠 수 있다. 이 효과는 감지를 위해 사용될 수 있지만 대개는 피한다.^[22] 전기적 및 유전적 경계 조건을 잘 제어하는 것이 필수적이다. 전면 전극(시료와 접촉하는 전극)의 접지도 한 가지 옵션이다. π 네트워크도 같은 이유로 채용되는 경우가 있다.^[23] π-네트워크는 저항기의 배열로, 두 전극을 거의 단락시킨다. 이것은 장치가 전기적 동요에 덜 취약하게 만든다.

액체 및 기체의 전단파 붕괴

대부분의 음향파 기반 센서는 전단파(횡단파)를 사용한다. 전단파는 액체와 기체 환경에서 빠르게 붕괴한다. 압축파(종방향)는 대량으로 방사되며, 잠재적으로 반대쪽 세포벽에서 결정으로 반사될 수 있다.^[24][25] 그러한 반사는 횡파로 피한다. 5 MHz-쉘 파동의 물 침투 범위는 250 nm이다. 이 유한한 침투 깊이는 QCM 표면 특정으로 렌더링한다. 또한 액체와 기체는 전단음향 임피던스가 다소 작아서 진동만 약하게 축축하게 한다. 음향 공진기의 예외적으로 높은 Q-요인은 환경에 대한 약한 결합과 연결된다.

운전모드

QCM을 구동하는 경제적인 방법은 오실레이터 회로를 사용한다.^[26][27] 오실레이터 회로는 오실레이터가 클럭 역할을 하는 시간 및 주파수 제어 애플리케이션에서도 널리 사용된다. 다른 작동 모드로는 임피던스 분석,^[28] QCM-I 및 링다운 ^[29][30]QCM-D가 있다. 임피던스 분석에서 주행 주파수의 함수로서의 전기 전도성은 네트워크 분석기를 통해 결정된다. 공진 곡선을 전도도 곡선에 적합시킴으로써 공명의 주파수와 대역폭을 적합 파라미터로 얻는다. 링 다운에서는 신나는 전압이 갑자기 꺼진 후 전극 사이의 전압을 측정한다. 공명기는 붕괴 사인파를 방출하며, 여기서 공진 파라미터는 진동 기간과 붕괴 속도에서 추출된다.

에너지 트랩

수정의 앞면과 뒷면에 있는 전극은 대개 열쇠구멍 모양으로 되어 있어 공명기가 림보다 중앙에 더 두꺼워진다. 전극의 질량은 에너지 트래핑이라고 불리는 메커니즘에 의해 결정 디스크의 중심에 변위장을 구속한다.^[31] 두께-바닥 진동 진폭은 디스크 중앙에서 가장 크다. 이것은 질량 감도가 가장 작은 전극의 둘레 바로 바깥에서 0으로 완만하게 감소하면서 중앙에서도 정점을 찍은다는 것을 의미한다.^[32] 따라서 질량 민감도는 결정표면에 걸쳐 매우 불균일하며, 이 불균일성은 금속 전극의 질량 분포(혹은 비 평면 공진기의 경우 석영 결정 두께 그 자체)의 함수다. 에너지 트래핑은 크리스탈을 음향 렌즈로 바꾸고 파동은 크리스탈의 중심에 집중한다. 과도한 댐핑 없이 크리스털을 가장자리에 장착할 수 있으려면 에너지 트래핑이 필요하다. 에너지 트래핑은 다른 평면파 전선을 약간 왜곡시킨다. 평면 두께-시어 모드로부터의 편차는 변위 패턴에 휨 기여를 수반한다. 휨파는 인접한 매질로 압축파를 방출하는데, 이는 액체 환경에서 결정체를 운용할 때 문제가 된다.

오버톤스

평면 공진기는 다수의 오버톤에서 작동할 수 있으며, 일반적으로 결정 표면에 평행한 결절면의 수에 의해 인덱싱된다. 두 개의 결정 표면에서 서로 반대되는 부호 전하를 유도하기 때문에 홀수 고조파만 전기적으로 흥분할 수 있다. 오버톤은 공명기의 평면에 수직인 결절면을 갖는 조화 측면 대역(비동기 모드)과 구별되어야 한다. 이론과 실험 사이의 최상의 일치점은 n = 5와 n = 13 사이의 오버론 주문을 위해 광학적으로 광학적으로 광학적으로 광학한 결정으로 도달한다. 낮은 고조파에서는 에너지 트랩이 불충분하고, 고조파에서는 고조파 사이드 밴드가 주공명을 방해한다.

운동 진폭

측면 변위의 진폭은 거의 나노미터를 초과하지 않는다. 좀 더 구체적으로 말하자면

${\displaystyle u_{0}={\frac {4}{\왼쪽(n\pi \오른쪽)^{2}}dQ_{\mathrm{el}}}}$

u₀ 측면 변위 진폭, 오버론 순서 n, 압전 변형 계수 d, 품질 계수 Q, 전기 구동 진폭 U_el. 압전 변형률 계수는 AT-컷 쿼츠 결정의 경우 d = 3.1·10m^‑12/V로 주어진다. 진폭이 작기 때문에 스트레스와 스트레스는 보통 서로 비례한다. QCM은 선형 음향 범위에서 작동한다.

온도와 스트레스의 영향

음향 공진기의 공명 주파수는 온도, 압력 및 휨 스트레스에 따라 달라진다. 온도-주파수 커플링은 특수 크리스털 컷을 적용하여 최소화한다. 널리 사용되는 온도 보상 석영 절단기는 AT-cut이다. QCM의 작동에는 온도와 응력의 세심한 관리가 필수적이다.

AT-컷 크리스털은 특이하게 회전하는 Y축 컷으로, 크리스털 상단과 하단이 진동 시 반대 방향(두께 전단 진동)^[33][34]으로 움직인다. AT-컷 크리스털은 쉽게 제조된다. 그러나 이러한 극한 온도(상온 대비, ~25°C)의 온도 구배 때문에 생기는 내부 스트레스로 인해 쉽게 교란되기 때문에 고온과 저온에서 한계가 있다. 이러한 내부 응력 지점은 결정에서 바람직하지 않은 주파수 이동을 생성하여 정확도를 떨어뜨린다. 온도와 빈도의 관계는 세제곱이다. 입방 관계는 상온에 가까운 변곡점이 있다. 따라서 AT-컷 쿼츠 결정은 상온 또는 근접한 온도에서 작동할 때 가장 효과적이다. 상온 이상의 용도에 대해서는 수냉이 도움이 되는 경우가 많다.

응력 보상(SC)결정은 시스템이 고온에서 작동 중일 때 온도 구배로 인한 주파수 변화를 최소화하고 수냉 의존도를 낮추는 이중 회전 절단 방식으로 이용할 수 있다.^[35] SC 절삭 결정의 변곡점은 ~92 °C이다. 고온 변곡점 외에도 입방 관계가 부드러워지고 변곡점으로부터의 온도 편차의 영향을 덜 받는다. 그러나 제조 공정이 까다로워 더 비싸고 상업적으로 널리 보급되지 않는다.

전기화학 QCM

QCM은 다른 표면 분석 기기와 결합할 수 있다. 특히 전기화학 QCM(EQCM)이 발달했다.^[36][37][38] EQCM을 사용하여 전극을 통과하는 총 전하량에 대한 전기화학 반응 동안 전극 표면에 축적된 질량의 비율을 결정한다. 이 비율을 현재의 효율이라고 한다.

분산 프로세스의 수량화

QCM-I, QCM-D와 같은 고급 QCM의 경우 공진 주파수인_r f와 대역폭인 w를 모두 분석에 사용할 수 있다. 후자는 진동에서 에너지를 빼내는 과정을 정량화한다. 여기에는 홀더에 의한 댐핑과 전극 또는 결정 내부의 옴 손실이 포함될 수 있다. 문헌에서 w자체 이외의 일부 매개변수는 대역폭을 정량화하는 데 사용된다. Q-요인(품질 인자)은 Q = f/w로_r 주어진다. "분산 인자" D는 Q-요인의 역이다. D = Q⁻¹ = w/f_r. 반대역폭 γ은 γ = w/2이다. γ의 사용은 결정의 움직임을 지배하는 방정식의 복잡한 공식화에 의해 동기 부여된다. 복잡한 공명 주파수는 f_r^* = f_r + I γ으로 정의되며, 여기서 가상의 부분인 γ은 절반의 최대 대역폭이다. 복잡한 표기법을 사용하면 동일한 (복잡한) 방정식 집합 내에서 주파수 Δf와 대역폭 Δγ의 이동을 처리할 수 있다.

공진기의 운동 저항인 R도₁ 소산의 척도로 사용된다. R은₁ 첨단 발진기 회로를 기반으로 하는 일부 계측기의 출력 파라미터다. R은₁ 일반적으로 대역폭에 엄격히 비례하지는 않는다(BvD 회로에 따라야 하지만, 아래 참조). 또한 절대적으로 R₁(주파수가 아닌 전기적 수량)은 대역폭보다 교정 문제에 의해 더 심각한 영향을 받는다.^[39]

등가 회로

음향 공진기의 모델링은 흔히 동등한 전기 회로와 함께 발생한다.^[40] 등가 회로는 연속체 역학 설명^[41] 및 음향 반사성의 측면에서 설명과 대수적으로 동등하다.^[42] 그것들은 공명기의 특성 및 하중 시 그 변화를 그래픽으로 표현한다. 이러한 표현은 단순한 만화만이 아니다. 하중의 추가에 대응하여 공명 파라미터의 이동을 예측하는 툴이다.

등가 회로는 전자기계 유추에 구축된다. 저항기 네트워크를 통한 전류와 동일한 방식으로 이들의 배열과 인가 전압에서 기계적 요소 네트워크의 변위를 예측할 수 있으며, 네트워크 위상과 인가된 힘으로부터 기계적 요소 네트워크의 변위를 예측할 수 있다. 전기-기계적 비유가 전류를 흐르는 전압과 속도에 힘을 매핑한다. 힘과 속도의 비율을 "기계 임피던스"라고 부른다. 주: 여기서 속도는 음속이 아니라 변위의 시간 파생물을 의미한다. 또한 전기 음향 유추도 있는데, 그 안에서 응력(힘보다는 스트레스)이 전압에 매핑된다. 음향학에서는 힘이 영역으로 정규화된다. 응력과 속도의 비율은 (기계 임피던스와 유사하게) "음향 임피던스"라고 불러서는 안 된다. 왜냐하면 이 용어는 이미 물질의 속성_ac Z = cc와 음속의 밀도와 c 속도를 위해 사용되고 있기 때문이다. 결정 표면에서 응력과 속도의 비율을 로드 임피던스, Z라고_L 한다. 동의어 용어는 "표면 임피던스"와 "음향 부하"^[27]이다. 로드 임피던스는 일반적으로 재료 상수 Z_ac = ρc = (Gρ)^1/2와 같지 않다. 전파 평면파에 대해서만 Z와_L Z의_ac 값이 동일하다.

전자-기계적 비유를 통해 저항기, 인덕턴스 및 캐패시턴스의 기계적 등가물이 제공되며, 이 경우 대시팟( 드래그 계수, ξ_p), 포인트 질량(질량_p, m), 스프링(스프링 상수, κ로_p 수량화됨)이다. 대시보드의 경우, 정의에 의한 임피던스는 F의 힘과 (du/dt) 속도를 갖는 Z_m=F / (du/dt)이다_m. 진동 운동 u(t) = u₀ exp(iΩt)을 수행하는 점 질량의 경우, Z_m = iΩm이_p 있다. 스프링은_m Z =κ_p/(iΩ)에 따른다. 압전 커플링은 변압기로 묘사된다. 파라미터 φ로 특징지어진다. φ은 통상적인 변압기(회전비)에 대해서는 치수가 없는 반면, 전자기계 커플링의 경우 치수 충전/길이도 있다. 변압기는 기계 임피던스 Z가_m 전기 포트에서 전기 임피던스 Z로_el 나타난다는 점에서 임피던스 컨버터 역할을 한다. Z는_elel Z = φ² Z로_m 주어진다. 평면 압전 결정의 경우 φ = Ae/d_q 값을 취하고 여기서 e는 압전 응력 계수^[28](AT-컷 쿼츠의 경우 e = 9.65·10⁻² C/m²), d는_q 플레이트의 두께다. 변압기는 종종 명시적으로 묘사되지 않는다. 오히려 기계적 요소를 전기적 요소(캐패시터가 스프링 등을 대체함)로 직접 묘사한다.

전기-기계적 유추의 적용에는 함정이 있는데, 이는 네트워크가 어떻게 그려지는가와 관련이 있다. 샘이 대쉬팟에 끌리면 보통 두 원소를 직렬로 그린다. 그러나 전자-기계적 유추를 적용할 때는 두 요소를 병렬로 배치해야 한다. 두 개의 병렬 전기 요소에 대해 전류는 가법적이다. 대쉬팟 뒤에 스프링을 놓을 때 속도(= 전류)가 추가되므로 이 어셈블리는 병렬 네트워크로 표시되어야 한다.

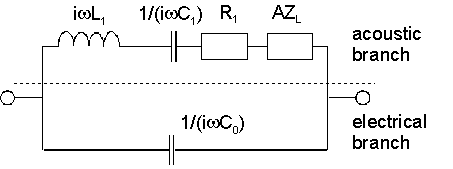
오른쪽 그림은 BvD(Butterworth-van Dyke) 등가 회로를 보여준다. 결정의 음향 특성은 모션 인덕턴스, L₁, 모션 캐패시턴스, C로₁ 표현되며 모션 저항₁ R. Z는_L 로드 임피던스다. 부하 Z는_L 단일 측정으로 결정할 수 없다는 점에 유의한다. 적재 상태와 적재되지 않은 상태의 비교에서 유추한다. 일부 저자는 부하_L Z 없이 BvD 회로를 사용한다. 이 회로를 "4요소 네트워크"라고도 한다. 그런₁ 다음 L₁, C₁, R 값은 부하가 있는 상태에서 값을 변경한다(원소_L Z가 명시적으로 포함되는 경우에는 그렇지 않음).

소부하 근사치

BvD 회로는 공명 파라미터를 예측한다. 주파수 그 자체보다 주파수 이동이 훨씬 작은 한 다음과 같은 단순한 관계가 유지된다는 것을 보여줄 수 있다.^[5]

${\displaystyle {\frac {\delta f^{*}{f_{f}}={\frac {i}{\pi Z_{q}}Z_{L}}}}$

f는_f 기본의 빈도다. Z는_q 물질의 음향 임피던스다. AT-컷 쿼츠의 경우, 그_q 값은 Z = 8.8·10⁶ kg m⁻²⁻¹ s이다.

소부하 근사치는 QCM 데이터 해석의 중심이다. 임의 샘플을 보관하고 있으며 평균적인 의미로 적용할 수 있다.^{[nb 1][43]} 표본이 세포배양, 모래더미, 거품, 구(球) 또는 방수( ves水)의 집합체, 물방울과 같은 복잡한 물질이라고 가정한다. 결정표면(부하 임피던스, Z_L)에서 표본의 평균 응력 대 속도 비율을 이런저런 방법으로 계산할 수 있다면 QCM 실험의 정량적 분석에 도달한다.^[44] 그렇지 않으면 그 해석은 질적으로 유지될 수밖에 없을 것이다.

소부하 근사치의 한계는 주파수 이동이 클 때 또는 Δf와 Δ(w/2)의 오버론 의존도를 상세히 분석하여 표본의 점탄성 특성을 도출할 때 주목한다. 좀 더 일반적인 관계는

${\displaystyle Z_{L}=-iZ_{q}\tan \left(\pi {\fracta f}{f}}}\오른쪽)}$

이 방정식은 Δf에 내포되어 있으며,^* 반드시 수치로 풀어야 한다. 근사치 해결책도 존재하며, 이는 소부하 근사치를 벗어난다. 소부하 근사치는 섭동 분석의 첫 번째 순서 솔루션이다.^[45]

부하 임피던스의 정의는 응력과 속도가 비례하여 그 비율이 속도와 무관하다고 암묵적으로 가정한다. 이 가정은 크리스탈이 액체와 공기로 작동될 때 정당화된다. 그러면 선형 음향의 법칙은 유지된다. 그러나 결정이 거친 표면에 닿으면 응력이 다소 작은 하중을 견디는 빈도의 유한한 수에 걸쳐 전달되기 때문에 스트레스는 쉽게 변형률(및 속도)의 비선형 함수가 될 수 있다. 접촉 지점에서의 응력이 높으며, 미끄러짐, 부분 미끄러짐, 항복 등의 현상이 나타나게 된다. 이것들은 비선형 음향의 일부분이다. 이 문제를 다루는 소부하 방정식의 일반화가 있다. 만약 스트레스인 ((t)이 시간적으로 주기적이며, 자신이 가지고 있는 결정 진동과 동기적이라면.

${\displaystyle {\fracta f}{f_{f}}={\frac {1}{\pi Z_{q}}\,{\frac {2}{\nomega u_{0}}}\langle \sigma \left(t\right)\cos \reft}$

${\displaystyle {\fracta(w/2)}{f_{f}}}={\frac {1}{\pi Z_{q}}\,{\frac {2}{\nomega u_{0}}}\langle \langle \left(t\opt)\{{t}}}}$

각괄호는 시간 평균을 나타내며 σ(t)은 외부 표면이 가하는 (작은) 응력이다. 함수 σ(t)는 조화가 될 수도 있고 아닐 수도 있다. 공진 매개변수가 주행 전압에 의존하는지 확인함으로써 비선형 거동을 항상 시험할 수 있다. 선형 음향 장치가 유지되면 드라이브 레벨에 의존하지 않는다. 그러나 쿼츠 결정에는 본질적인 드라이브 레벨 의존성이 있으므로 결정과 샘플 간의 비선형 상호작용과 혼동해서는 안 된다는 점에 유의하십시오.

점탄성 모델링

가정

많은 실험 구성의 경우, 샘플 속성에 대한 주파수 및 대역폭의 이동과 관련된 명시적 식이 있다.^{[46][47][48][49]} 방정식의 기초가 되는 가정은 다음과 같다.

• 공명기와 모든 피복층은 횡방향으로 균일하고 무한하다.
• 결정의 왜곡은 파장 벡터가 표면 정상(두께-표면 모드)에 수직인 횡단 평면 파형에 의해 발생한다. 변위 패턴에 대한 압축파도^[23][24] 휨 기여도 없다.^[50] 공명기의 평면에는 결절선이 없다.
• 모든 스트레스는 스트레인에 비례한다. 선형 점탄성은 유지된다.^[51]
• 압전 경직은 무시될 수 있다.

반무한 점탄성 매체

반무한 매체의 경우, 사람은^[52][53][54]

${\displaystyle {\frac {\Delta f^{*}}{f_{f}}}={\frac {i}{\pi Z_{q}}}\,{\frac {\sigma }{\dot {u}}}={\frac {i}{\pi Z_{q}}}Z_{\mathrm {ac} }={\frac {i}{\pi Z_{q}}}{\sqrt {\rho i\omega \eta }}}$

${\displaystyle ={\frac {1}{\pi Z_{q}}\,{\frac {-1+i}{\rho \rho \omega \left(\eta ^{\eta ^}-i\eta ^{\premium \primium \}}\primium }\}\}\crimprimyprimium }\}\right)}}}={\frac {i}{\pi Z_{q}}{\sqrt {\rho \left(G^{\premium }+iG^{\prime \prime \prime \primium }\primium \primyprime}\}\}}}}$

η'과 η'은 각각 점도의 실제와 상상의 부분이다. Z_ac = ρc =(G ρ)^1/2는 매질의 음향 임피던스다. ρ은 밀도, c, 음속의 속도, G = i Ωη은 전단계수다. 뉴턴 액체의 경우(η' = const, η' = 0), Δf와 Δ(w/2)는 동일하고 반대다. 그들은^1/2 오버톤 질서의 제곱근으로 확장된다. 점성 액체( for' = η(Ω), η'≠ 0)의 경우 복합 점도는 다음과 같이 구할 수 있다.

${\displaystyle \eta ^{\py ^}=-{\frac {\pi Z_{q}^{2}}:{\rho_{\mathrm {Liq}\\}\f}\{\frac {\Delta f\delta \lef(w/2\오른쪽)}{f}{f}:{2}}:$

${\displaystyle \eta ^{\prime \prime }={\frac {1}{2}}{\frac {\pi Z_{q}^{2}}{\rho _{\mathrm {Liq} }\,f}}\,{\frac {\left(\left(\Delta \left(w/2\right)\right)^{2}-\Delta f^{2}\right)}{f_{f}^{2}}}}$

중요한 것은, QCM은 결정 표면에 가까운 영역만 탐사한다는 것이다. 전단파는 갑자기 액체로 분해된다. 물에서 침투 깊이는 5 MHz에서 약 250 nm이다. 표면 거칠기, 표면의 나노 버블, 미끄러짐, 압축파 등은 점도의 측정을 방해할 수 있다. 또한 MHz 주파수에서 결정되는 점도가 저주파 점도와 다른 경우도 있다. 이 점에서 비틀림 공명기^[20](주파수가 약 100 kHz)는 두께-헤어 공진기보다 적용에 가깝다.

관성하중(Sauerbrey 방정식)

결정(예: 박막)에 단단하게 결합되는 얇은 샘플에 의해 유도되는 주파수 이동은 사우어브레이 방정식으로 설명된다. 응력은 σ = -Ωum을²_0F 의미하는 관성에 의해 제어된다. 여기서 u는₀ 진동 진폭이고 m은_F 단위 면적당 (평균) 질량이다. 이 결과를 찾은 작은 부하 근사치에 삽입

${\displaystyle {\frac {\Delta f^{*}}{f_{f}}}\approx {\frac {i}{\pi Z_{q}}}{\frac {-\omega ^{2}u_{0}m_{\%\mathrm {F} }}{i\omega u_{0}}}=-{\frac {2\,f}{Z_{q}}}m_{\mathrm {F} }}$

필름의 밀도가 알려지면 단위 면적당 질량(m_F)에서 두께 d로_F 변환할 수 있다. 이렇게 파생된 두께를 Sauerbrey thickness라고도 부르는데, 이는 주파수 이동에 Sauerbrey 방정식을 적용하여 파생된 것임을 보여준다. 사우어브레이 방정식이 유지된다면 대역폭의 변화는 0이다. 따라서 대역폭을 확인하는 것은 Sauerbrey 방정식의 적용 가능성을 확인하는 것과 같다.

사우어브레이 방정식은 1959년 귄터 사우어브리에 의해 처음 도출되었으며 압전 결정의 진동 주파수 변화와 그 위에 축적된 질량의 상관관계를 가진다. 그는 크리스탈을 오실레이터 회로의 주파수 결정 요소로 사용하여 공명 주파수와 그 변화를 측정하는 방법을 동시에 개발했다. 그의 방법은 주파수를 질량으로 변환하기 위한 석영 결정 마이크로밸런스 실험에서 계속해서 1차 도구로 사용되고 있다.

필름을 두께의 확장으로 취급하기 때문에, Sauerbrey의 방정식은 (a) 축적된 질량이 결정과 동일한 음향 특성을 가지고 있고 (b) 주파수 변화가 작은 시스템(Δf / f < 0.05)에만 적용된다.

주파수 변화가 5% 이상일 경우, 즉 Δf / f > 0.05 이상일 경우 질량 변화를 판단하기 위해 Z 일치 방법을 사용해야 한다.^[9][54] Z 일치 방법의 공식은 다음과 같다.

${\dplaystyle \tan \left({\frac {\pi \Delta f}{f_}}}\right}={\frac {-Z_{q}}}}}}}}}\tan \left(k_{mathrm}{F}{F}}}}\mathrmathrmathrmatrmatmatmatmatmatrmatmatmatm) {F}}}}}\rig}\rig}\rig)$

k는_F 필름 내부의 파동 벡터로서 두께가 d이다_F. k_F = 2·164·f /c_F = 2·164·f_F·16_F / Z와_F d_F = m / ρ_F 수율

${\displaystyle \Delta f=-{\frac {f_{f}}{\pi }}\left(\arctan {\frac {Z_{\mathrm {F} }}{Z_{q}}}\tan \left({\frac {2\pi f}{Z_{\mathrm {F} }}}m_{\mathrm {F} }\right)\right)}$

점탄성 필름

점탄성 필름의 경우 주파수 시프트는

${\displaystyle {\frac {\delta f^{*}{f_{f}}}={\frac {-1}{\pi Z_{q}}}}Z_{\mathrm {F}}}}\tan \left(k_{\mathrmatrm {F}}}}\rig)$

여기서 Z는_F 필름의 음향 임피던스(Z_F = ρc_FF = (ρG_Ff)=^1/2 (ρG)= (ρ_F/J_f)),^1/2 k는_F 파동 벡터, d는_F 필름 두께다. J는_f 이 영화의 점탄성 준수, is은_F 밀도다.

접선의 극(k_F d_F = π/2)은 필름 공진을 정의한다.^[55][56] 필름 공명에서는 d_F = λ/4가 있다. 실험과 이론의 일치점은 종종 영화 공명에 가깝지 않다. 일반적으로 QCM은 소리의 파장의 1/4보다 훨씬 작은 필름 두께에 대해서만 잘 작동한다(필름의 부드러움과 오버론 오더에 따라 몇 마이크로미터에 대응함).

QCM으로 결정되는 필름의 속성은 음향 임피던스 Z_F = cc와_FF 단위 면적당 질량_F m = d_F/d인_F 두 파라미터로 완전히 지정된다는 점에 유의하십시오. 파형 번호 k_F = Ω/c는_F Z와_F m에서_F 대수적으로 독립적이지 않다. 필름의 밀도를 독립적으로 알 수 없는 한 QCM은 단위 면적당 질량을 측정할 수 있을 뿐 기하학적 두께 자체는 절대 아니다.

액체 속의 점탄성 필름

액체 환경에 몰입한 필름의 경우 주파수 시프트는^[57][58]

${\displaystyle {\frac {\Delta f^{*}}{f_{f}}}={\frac {-Z_{\mathrm {F} }}{\pi Z_{q}}}{\frac {Z_{\mathrm {F} }\tan \left(k_{\mathrm {F} }d_{\mathrm {F} }\right)-iZ_{\mathrm {Liq} }}{Z_{\mathrm {F} }+iZ_{\mathrm {Liq} }\tan \left(k_{\mathrm {F} }d_{\mathrm {F} }\right)}}}$

F와 Liq 지수는 필름과 액체를 나타낸다. 여기서 기준 상태는 액체에 담근 결정(필름으로 덮이지 않음)이다. 박막의 경우 테일러가 위의 방정식을 d로_F 첫 번째 순서로 확장하여 양보할 수 있다.

${\displaystyle {\frac {\Delta f^{*}}{f_{f}}}={\frac {-m_{\mathrm {F} }}{\pi Z_{q}}}\left(1-{\frac {Z_{\mathrm {Liq} }^{2}}{Z_{\mathrm {F} }^{2}}}\right)={\frac {-m_{\mathrm {F} }}{\pi Z_{q}}}\left(1-J_{\mathrm {F} }{\frac {Z_{\mathrm {Liq} }^{2}}{\rho _{\mathrm {F} }}}\right)}$

괄호 안의 항을 제외하고, 이 방정식은 사우어브레이 방정식과 동등하다. 괄호 안의 용어는 액체에서 부드러운 층이 단단한 층보다 작은 사우어브레이 두께로 이어진다는 사실을 다루는 점탄성 보정이다.

점탄성 상수의 유도

주파수 이동은 소재의 음향 임피던스에 따라 달라지며, 후자는 소재의 점탄성 특성에 따라 달라진다. 따라서 원칙적으로 복잡한 전단계(또는 동등하게 복잡한 점성)를 도출할 수 있다. 그러나 명심해야 할 몇 가지 주의사항이 있다.

• 점탄성 매개변수 자체는 대개 주파수(따라서 명시적 순서)에 따라 달라진다.
• 관성과 점탄성의 영향을 분리하는 것은 종종 어렵다. 필름 두께를 독립적으로 알지 않는 한 고유한 피팅 결과를 얻기 어렵다.
• 전극 효과가 중요할 수 있다.
• 공기 중에 있는 필름의 경우 필름이 매우 부드럽지 않은 한 소부하 근사치를 섭동 이론의 해당 결과로 대체해야 한다.

액체의 박막의 경우 필름의 탄성 준수와 Δ(w/2)의 비율에 대한 J_F'와 Δf와 관련된 대략적인 분석 결과가 있다. 전단 적합성은 전단 계수 G의 역행이다. 박막 한계에서 Δ(w/2)와 –Δf의 비율은 필름 두께와 무관하다. 그것은 그 영화의 본질적인 특성이다. 가지고^[59] 있다

${\displaystyle {\fract {\delta \left(\omega /2\오른쪽)}{-\Delta f}\\cHBFF}^{\\prime}}}}}$

공기^[60] 중의 박막의 경우 유사한 분석 결과가

${\displaystyle \Delta \left(\omega /2\오른쪽)={\frac {8}{3\rho_{\matrm {F}{{q}f}^{f}^{\4}m_{{3}n^{3}\pi{2}J^{primeprim}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}primefrimefrimefrimeprimefrim$

여기 J''는 점성 전단 준수다.

사우어브레이 두께 해석

QCM 실험에서 나오는 주파수 이동에 대한 정확한 해석은 도전이다. 실무자들은 흔히 Sauerbrey 방정식을 데이터에 적용하고 결과 면적 질량(단위 면적당 질량), "Sauerbrey 질량" 및 해당 두께 "Sauerbrey 두께"를 용어화한다. Sauerbrey 두께는 확실히 다른 실험을 비교하는 데 도움이 될 수 있지만, 기하학적 두께로 순진하게 식별되어서는 안 된다. 가치 있는 고려사항은 다음과 같다.

a) QCM은 항상 면적 질량 밀도를 측정하며 기하학적 두께는 측정하지 않는다. 면적 질량 밀도에서 두께로 변환하려면 일반적으로 독립적인 입력으로서 물리적 밀도가 필요하다.

b) QCM 데이터에서 점탄성 보정 계수를 유추하기 어렵다. 단, 보정계수가 단결성과 크게 다를 경우, 대역폭 Δ(w/2)에 영향을 미치고 또한 오버론 오더에 의존한다고 예상할 수 있다. 반대로 그러한 영향이 없는 경우(Δ(w/2_F²) Δf, 사우어브레이 두께는 모든 오버론 주문에서 동일) Δ1로_Liq² 가정할 수 있다.

c) 복잡한 시료는 종종 횡으로 이질적인 경우가 많다.

d) 복잡한 시료는 종종 흐릿한 인터페이스를 가진다. "불투명한" 인터페이스는 종종 점탄성 보정을 초래하고 그 결과, 0이 아닌 Δ(w/2)는 물론 지나치게 의존적인 Sauerbrey 질량으로 이어진다. 그러한 효과가 없을 경우, 필름의 외부 인터페이스가 날카롭다고 결론을 내릴 수 있다.

e) (b)에서 논한 바와 같이 점탄성 보정이 경미한 경우, 이는 결코 필름이 용매에 의해 부풀지 않았음을 의미하지 않는다. 단지 (스울렌) 필름이 주위 액체보다 훨씬 단단하다는 것을 의미할 뿐이다. 습식 샘플에 대한 QCM 데이터만으로는 붓기 정도를 추론할 수 없다. 부기의 양은 젖은 두께와 마른 두께를 비교한 것으로 유추할 수 있다. 부기의 정도는 표면 플라스몬 공명(SPR) 분광법이나 타원측정법에 의해 결정되는 광학 두께와 음향 두께(Sauerbrey 의미)를 비교하여도 접근 가능하다. 필름에 포함된 용제는 일반적으로 음향 두께에 기여하는 반면(이동 중 참여하기 때문에), 시신 두께에는 기여하지 않는다(용제 분자의 전자 편광성은 필름 내부에 위치할 때 변하지 않기 때문이다). 건조 질량과 습식 질량의 차이는 예를 들어 나노셀룰로오스의^[61][62] 단백질 흡착과 다른 부드러운 물질에서 QCM-D와 MP-SPR로 나타난다.^[63]

포인트 연락처

점탄성 특성에 관한 방정식은 평면 레이어 시스템을 가정한다. 또한 결정이 하중을 견디는 작은 빈도에 걸쳐 이산 물체와 접촉할 때 주파수 이동이 유도된다. 그러한 접촉은 종종 거친 표면과 마주친다. 응력 속도비는 평균 응력 속도비로 대체될 수 있다고 가정하며, 여기서 평균 응력은 결정의 활성 영역으로 나눈 횡력이다.

종종 외부 물체가 너무 무거워서 관성으로 인한 결정의 MHz 진동에는 관여하지 않는다. 그런 다음 실험실 프레임에 놓인다. 결정 표면이 횡방향으로 이동될 때, 접촉은 결정 표면에 복원력을 발휘한다. 응력은 접점 밀도 N과_S 이들의 평균 스프링 상수인 κ에_S 비례한다. 스프링 상수는 복잡할 수 있으며(예_S^*_S: 점탄성_S 효과로 인해) 상상의 부분은 결정 진동에서 에너지의 철수를 정량화한다. 그러한 상황에 대해 작은 부하 근사치는 예측한다.

${\displaystyle {\fraca {\delta f^{*}{f_{f}}={\frac {N_{S}}{\pi Z_{q}}}{\frac {\cappa _{S}^{S}}}}}{\opega }}}}}}}}}}}}}}}}}}$

QCM은 다중 파괴 접점의 전단 강성에 대한 비파괴 시험을 허용한다.

참고 항목

• 사우어브레이 방정식
• 사우어브레이 상수
• 사우어브레이 층
• 체중계
• 압전성
• 박막 두께 모니터
• 방산 모니터링(QCM-D)이 포함된 쿼츠 크리스털 마이크로 밸런스
• 테이퍼 소자 진동 마이크로 밸런스(TEOM)

메모들

참조

추가 읽기

• Quartz Crystal Microbalance with Dissolation monitoring
• 웨이백 머신에서 QCM이란?(2007년 6월 29일 보관)
• 웨이백 머신에서 쿼츠 크리스털 마이크로밸런스(2009년 8월 14일 보관)
• 아카이브에서 박막 증가를 모니터링하기 위한 진공 애플리케이션(HV 및 UHV)용 Quartz crystal 마이크로밸런스 오늘(2013년 2월 3일 아카이브)
• 오늘(2013년 1월 6일 자료 보관)에서 QCM의 동작을 모델링하는 자습서
• 임피던스 분석 및 소산 모니터링을 통한 QCM-I의 원리

외부 링크

• QCM 미니 FAQ