구조강성
Structural rigidity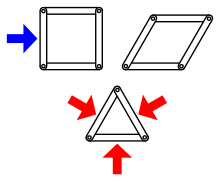
이산형 기하학 및 역학에서 구조 강성은 유연한 링크나 경첩에 의해 연결된 강체로 형성된 앙상블의 유연성을 예측하기 위한 결합 이론이다.
정의들
강성은 적용된 힘 하에서 구부러지거나 구부러지지 않는 구조물의 특성이다. 경직성의 반대는 유연성이다. 구조 강성 이론에서 구조는 직선 막대(선형 세그먼트)와 같은 단순한 기하학적 형태를 취하는 것으로 가정되는, 스스로 강체인 물체의 집합에 의해 형성되며, 유연한 경첩에 의해 연결된 물체의 쌍을 가지고 있다. 구조물은 구부릴 수 없는 경우 경직된다. 즉, 경첩에서 단단한 구성 요소의 모양과 연결부의 패턴을 보존하는 구조물의 연속적인 움직임이 없는 경우.
본질적으로 다른 두 종류의 경직성이 있다. 유한 또는 거시적 강성은 구조가 양의 양만큼 구부러지거나 접히거나 구부러지지 않는다는 것을 의미한다. 극소 강성은 이론상으로도 감지할 수 없을 정도로 작은 양으로도 구조가 굴절되지 않는다는 것을 의미한다.(기술적으로 그것은 특정 미분방정식에 0이 아닌 용액이 없다는 것을 의미한다) 유한 강성의 중요성은 명백하지만, 이론상 극히 적은 유연성이 실제의 극소량 굴곡과 그에 따른 구조물의 열화에 해당하기 때문에 극소수의 강성도 또한 중요하다.
강체 그래프는 구조적으로 강체인 유클리드 공간에 그래프를 내장한 것이다.[1] 즉, 가장자리를 강성봉으로 교체하여 형성된 구조와 유연한 경첩에 의한 정점이 강성이면 그래프가 강성이다. 경직되지 않은 그래프를 플렉시블이라고 한다. 좀 더 공식적으로, 정점을 연속적으로 이동할 수 있는 경우, 인접 정점 사이의 거리를 보존하고, 일부 비인접 정점 사이의 거리가 변경되는 결과를 가진 경우 그래프 임베딩은 유연하다.[2] 후자의 조건은 간단한 번역과 회전과 같은 유클리드적 합성을 배제한다.
또한 일부 가장자리는 압축 요소(더 긴 길이까지 확장할 수 있지만 더 짧은 길이로 수축할 수는 없음)를 나타내는 그래프와 다른 가장자리는 장력 요소(축소할 수는 있지만 늘어나지 않는 것)를 나타내는 그래프에 대해서도 경성 문제를 고려할 수 있다. 이러한 유형의 가장자리가 있는 강체 그래프는 시제 그래프의 수학적 모델을 형성한다.
경성수학
구조물을 지을 필요 없이 이론적 분석을 통해 구조물의 경직성을 어떻게 예측하느냐가 근본적인 문제다. 이 영역의 주요 결과는 다음과 같다.
- 어떤 차원에서도 로드 앤 힝기 연결의 강성은 매트로이드로 설명된다. 2차원 강성 매트로이드(평면의 최소 강성 그래프)의 기초는 라만 그래프다.
- 코치의 정리에는 얼굴 가장자리를 따라 경첩으로 연결된 단단한 판으로 구성된 3차원 볼록 다면체가 단단한 구조를 형성한다고 되어 있다.
- 융통성 있는 폴리헤드라, 단단하지 않은 비콘벡스 폴리헤드라는 라울 브리카드, 로버트 코넬리 등이 시공했다. 현재 입증된 벨로우즈 추측에 따르면, 유연한 다면체의 어떤 연속적인 움직임도 그 부피를 보존해야 한다고 한다.
- 경직될 프레임워크가 교차 브레이싱으로 대각선이 추가된 사각 격자인 그리드 브레이싱 문제에서 구조물의 경직성은 기초적인 양분 그래프의 연결성에 관한 문제로 번역함으로써 분석할 수 있다.[3][4]
그러나, 다른 많은 단순한 상황에서 상당한 수학 이론이 존재함에도 불구하고 구조물의 경직성을 수학적으로 분석하는 방법은 아직 항상 알려져 있지 않다.
역사
구조 경직성의 수학적 이론의 창시자 중 한 명은 위대한 물리학자 제임스 서클 맥스웰이었다. 20세기 후반에는 21세기에도 계속되는 경직성에 대한 수학 이론의 허울이 사라졌다.
"힘의 작용에 따른 골격의 평형 및 편향 이론은 품질의 경직성에 영향을 미치고 있다. 그 틀이 ...인 경우에는. 추가 연결 조각에 의해 강화되다... 3차원의 경우, 힘의 정규방정식에 의해, 모든 점에는 평형을 결정하기 위한 3개의 방정식이 있을 것이고, 만약 s가 점의 수와 연결의 수인 경우 e 미지의 수량 사이에 3s 방정식을 제공할 것이다. 그러나 각 조각의 작용과 반작용의 균등성 때문에 반드시 힘에 의해 충족되어야 하는 6개의 계통 평형 방정식이 있다. 따라서 e==3s-6이면 영원한 힘의 영향은 여러 조각에서 긴장이나 압력을 생성하는 데 분명할 것이다. 그러나 e>3s-6이면 이러한 힘은 확실치 않을 것이다."[맥스웰 1864년][citation needed]
참고 항목
메모들
- ^ Weisstein, Eric W. "Rigid Graph". MathWorld.
- ^ Weisstein, Eric W. "Flexible Graph". MathWorld.
- ^ Baglivo, Jenny A.; Graver, Jack E. (1983), "3.10 Bracing structures", Incidence and Symmetry in Design and Architecture, Cambridge Urban and Architectural Studies, Cambridge, UK: Cambridge University Press, pp. 76–87, ISBN 9780521297844
- ^ Graver, 잭 E.(2001년), 골조에 계산하는 것:수학 에이드에 강체 구조물, 그 Dolciani 수학 Expositions의 설계, 25vol., 워싱턴, DC:수학 협회는 미국의, 아이 에스비엔 0-88385-331-0, MR1843781.특정 섹션 1.2("송전망은 상쾌한 문제",를 대신하여 서명함. 4–12), 1.5("더욱 그리드 문제에 대해",를 대신하여 서명함. 19–22), 2.6("스마트 그리드는 전력망 문제의 해결책은",를 대신하여 서명함. 50–55), 4.4("텐서:긴장 bracings", 특히를 대신하여 서명함. 158–161)을 보세요.
참조
- Alfakih, Abdo Y. (2007), "On dimensional rigidity of bar-and-joint frameworks", Discrete Applied Mathematics, 155 (10): 1244–1253, doi:10.1016/j.dam.2006.11.011, MR 2332317.
- Connelly, Robert (1980), "The rigidity of certain cabled frameworks and the second-order rigidity of arbitrarily triangulated convex surfaces", Advances in Mathematics, 37 (3): 272–299, doi:10.1016/0001-8708(80)90037-7, MR 0591730.
- Crapo, Henry (1979), "Structural rigidity", Structural Topology (1): 26–45, 73, hdl:2099/521, MR 0621627.
- Maxwell, J. C. (1864), "On reciprocal figures and diagrams of forces", Philosophical Magazine, 4th Series, 27 (182): 250–261, doi:10.1080/14786446408643663.
- Rybnikov, Konstantin; Zaslavsky, Thomas (2005), "Criteria for balance in abelian gain graphs, with applications to piecewise-linear geometry", Discrete and Computational Geometry, 34 (2): 251–268, arXiv:math/0210052, doi:10.1007/s00454-005-1170-6, MR 2155721, S2CID 14391276.
- Whiteley, Walter (1988), "The union of matroids and the rigidity of frameworks", SIAM Journal on Discrete Mathematics, 1 (2): 237–255, doi:10.1137/0401025, MR 0941354



