비서문제

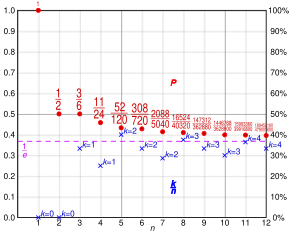
비서 문제는 응용 확률, 통계, 결정 이론 분야에서 광범위하게 연구되는 최적 정지 이론을^[1][2] 포함하는 시나리오를 보여줍니다.결혼 문제, 술탄의 지참금 문제, 까다로운 구걸 문제, 최선의 선택 문제라고도 합니다.

문제의 기본 형태는 다음과 같습니다. ${\displaystyle n}$ 순위가$$ 매겨진 지원자 중에서 최고의 비서를 채용하려는 관리자를 상상해 보십시오.지원자들은 무작위로 한 명씩 면접을 봅니다.면접 직후에 각 지원자에 대한 결정이 내려져야 합니다.신청자는 일단 기각되면 회수할 수 없습니다.면접 과정에서 관리자는 지금까지 면접한 모든 지원자 중에서 지원자의 순위를 매길 만큼 충분한 정보를 얻지만, 아직 보지 못한 지원자의 자질에 대해서는 알지 못합니다.문제는 가장 적합한 지원자를 선택할 확률을 최대화하기 위한 최적의 전략(정지 규칙)에 대한 것입니다.결정을 끝까지 미룰 수 있다면, 이는 실행 중인 최대치(그리고 누가 달성했는지)를 추적하고, 마지막에 전체 최대치를 선택하는 간단한 최대 선택 알고리즘으로 해결할 수 있습니다.문제는 결정이 즉각 내려져야 한다는 것입니다.

지금까지 알려진 가장 짧은 엄격한 증명은 오즈 알고리즘에 의해 제공됩니다.최적의 승리 확률은 항상 최소 $1{\displaystyle \mathrm{}/e}$ ${\displaystyle 1/e}($여기서 e는 자연 로그의 기본)이며 후자는 훨씬 더 큰 일반성에서도 성립함을 의미합니다.최적 정지 규칙은 면접을 본 첫 ${\displaystyle \mathrm{번째}}$ ~${\displaystyle n}$/ e ${\displaystyle \sim n$/ $e}$명의$$ 지원자를 항상 거부한 후 지금까지 면접을 본 모든 지원자보다 나은 첫 번째 지원자에게 정지(또는 이런 일이 일어나지 않을 경우 마지막 지원자에게 계속)하도록 규정합니다.때때로 이 전략은 ${\displaystyle 1}$/ e ${\displaystyle 1/e}$ 정지$$ 규칙이라고 불리는데, $왜냐하면{\displaystyle }$ 이 전략으로 가장 좋은 지원자가 정지할 확률은 n$${\$displaystyle n}$의 중간 값에 $대해$ 이미${\displaystyle }$1 / ${\displaystyle e}${\$displaystyle$ 1$/e}$이기 때문입니다$.$ 비서 문제가 이렇게 주목을 받는 이유 중 하나는 p에 대한 최적 정책 때문입니다.문제(정지 규칙)는 단순하며 지원자가 1억 명이든 1억 명이든 관계없이 약 37%의 시간 동안 단일 최적 후보를 선택합니다.

공식화

여러 가지 변형이 있지만 기본적인 문제는 다음과 같이 설명할 수 있습니다.

• 채워야 할 자리가 하나 있습니다.
• 그 자리에 지원자가 n명이고, n의 값이 알려져 있습니다.
• 지원자들은, 모두 함께 본다면, 분명하게 최고에서 최악의 순위를 매길 수 있습니다.
• 지원자들은 무작위 순서로 순차적으로 면접을 받으며, 각 순서는 동일하게 진행됩니다.
• 면접 직후 면접 지원자는 합격 또는 불합격 처리되며, 그 결정은 취소할 수 없습니다.
• 지원자의 합격 또는 불합격 결정은 지금까지 면접한 지원자들의 상대적인 순위만을 기준으로 할 수 있습니다.
• 일반적인 솔루션의 목적은 전체 그룹 중에서 가장 적합한 지원자를 선택할 확률이 가장 높은 것입니다.이는 예상 보수를 최대화하는 것과 같으며, 최고의 지원자에게는 보수를, 그렇지 않으면 0으로 정의됩니다.

지원자는 이전에 면접을 본 모든 지원자들보다 면접을 잘 본 지원자로 정의됩니다.스킵은 "인터뷰 후 즉시 거절"이라는 뜻으로 사용됩니다.문제의 목표는 단일 최우수 지원자를 뽑는 것이기 때문에, 합격자는 후보자들만 고려할 것입니다.이러한 맥락에서 "후보자"는 순열에서의 기록의 개념에 해당합니다.

최적 정책 도출

문제에 대한 최적의 정책은 중지 규칙입니다.그 아래 면접관은 첫 번째 r - 1 지원자를 거부하고(이들 r - 1 지원자 중에서 지원자 M이 가장 우수한 지원자가 되도록 하라), 다음에 지원자 M보다 더 나은 첫 번째 후속 지원자를 선택합니다.최적의 전략은 이 부류의 전략에 있음을 알 수 있습니다.^{[citation needed]}(전체적으로 최고의 지원자가 될 수는 없기 때문에 지금까지 본 지원자 중 최고가 아닌 지원자를 절대로 선택해서는 안 됩니다.)임의 절단자의 경우, 가장 적합한 지원자가 선택될 확률은

${\displaystyle {\begin{aligned}P(r)&=\sum _{i=1}^{n}P\left({\text{applicator}}}i{\text{selected}}\cap {\text{applicant }i{\text{ is best}}\right)\&=\sum _{i=1}^{n}P\left({\text{응용자}}}i{\text{선택되었습니다}{\text{applicant }}i{\text{ is 뭔들}\right)\cdot P\left({\text{응용자}}i{\text{ is 뭔들}\right)\\&=\left[\sum _{i=1}^{r-1}0+\sum _{i=r}^{n}P\left(\left).{\begin{array}{l}{\text{첫 번째 }}{i-1{\text{응용자}}\{\text{는 첫 번째 }}r-1{\text{응용자}}\end{array}}\right{\text{가 가장 좋습니다}\right}\cdot{\frac{1}{n}\&=\left]\cdot{{i=r}^{n}{\frac{r-1}}\right]\cdot{\frac{1}{n}}\&={\frac{r-1}{n}}\sum{i=r}^{n}{\frac{1}}}\sum{i=r}^{n}{\frac{1}}.\end{aligned}}$

합은 r = 1에 대해 정의되지 않지만, 이 경우 유일하게 실현 가능한 정책은 첫 번째 지원자를 선택하는 것이므로 P(1) = 1/n입니다.이 합계는 지원자 i가 가장 우수한 지원자인 경우, 첫 번째 i - 1 지원자 중 가장 우수한 지원자가 거부된 첫 번째 r - 1 지원자 중에 있는 경우에만 선택된다는 점에 주목함으로써 얻어집니다.n이 무한대가 되도록 하고 $x{\displaystyle }$ ${\displaystyle x}$를 (r-1)/n의 극한으로 쓰고 (i-1)/n을 t로 하고 1/n을 dt로 하면 합은 적분으로 근사할 수 있습니다.

${\displaystyle P(x)=x\int _{x}^{1}{\frac {1}{t}}\,dt=-x\ln(x)\;.}$

$x{\displaystyle }$ ${\displaystyle x}$에 대하여 P(x)의 도함수를$$취하여 0으로 설정하고 x에 대하여 풀면, 최적 x는 1/e와 같다는 것을 알 수 있습니다.따라서 최적 컷오프는 n이 증가함에 따라 n/e로 경향이 있으며, 최적 지원자는 확률 1/e로 선택됩니다.

n의 작은 값의 경우 표준 동적 프로그래밍 방법을 통해 최적 r을 얻을 수도 있습니다.n의 여러 값에 대해 최적의 대안 P를 선택할 수 있는 최적 임계값 r과 확률이 다음 표에 나와 있습니다.^{[note 1]}

${\displaystyle n}$	1	2	3	4	5	6	7	8	9	10
${\displaystyle r}$	1	1	2	2	3	3	3	4	4	4
${\displaystyle P}$	1.000	0.500	0.500	0.458	0.433	0.428	0.414	0.410	0.406	0.399

고전적인 비서 문제에서 가장 적합한 지원자를 선택할 확률은 $1{\displaystyle /e}$ ≈ ${\displaystyle 0.368}$ ${\displaystyle 1/e\약 0.368}$로 수렴합니다$.$

대안해

이 문제와 몇 가지 수정 사항은 다른 응용 프로그램도 있는 오즈 알고리즘에 의해 간단한 방식으로 해결할 수 있습니다(최적성의 증명을 포함하여.이 알고리즘에 의해 해결될 수 있는 비서 문제에 대한 수정에는 지원자의 무작위 가용성, 의사 결정자가 관심을 가질 수 있는 보다 일반적인 가설, 지원자를 위한 그룹 인터뷰 및 무작위 수의 지원자를 위한 특정 모델이 포함됩니다.^{[citation needed]}

한계

비서 문제의 해결은 지원자들이 의사결정 전략에 대해 전혀 알지 못한다고 가정하는 것이 정당한 경우에만 의미가 있습니다. 왜냐하면 초기 지원자들은 전혀 기회가 없고 그렇지 않으면 나타나지 않을 수 있기 때문입니다.

고전적인 비서 문제의 해결책을 응용할 때 한 가지 중요한 단점은 ${\displaystyle n}$ $지원자$의 수를 미리 알아야 한다는$$ 것이며, 이는 거의 그렇지 않습니다.이 문제를 극복하기 위한 하나의 방법은 지원자의 수를 P${\displaystyle (N}$ = ${\displaystyle k{}_{}}$ ${\displaystyle k_{}}$ = ${\displaystyle {1,}_{}}$ ${\displaystyle 2_{}}$,${\displaystyle {}_{}}$⋯ ${\displaystyle P(N$= k$)_{k$ = $1,$ 2$,\cdots }}$의 알려진 분포를 갖는 랜덤 변수 $N$ ${\displaystyle N}$이라고 가정하는 것입니다(Presman and Sonin, 1972).그러나 이 모델의 경우 일반적으로 최적 솔루션이 훨씬 더 어렵습니다.또한 최적의 성공 확률은 이제 더 이상 1/e 정도가 아니라 일반적으로 더 낮습니다.이는 지원자 수를 모르는 것에 대한 '대가'가 있다는 맥락에서 이해할 수 있습니다.하지만 이 모델은 가격이 높습니다.$N{\displaystyle }$ ${\displaystyle N}$ 분포의 선택에 따라 최적 승 확률이 0에 가까워질 수 있습니다$.$이 새로운 문제에 대처할 수 있는 방법을 모색하던 중, 이른바 1/e-law of best selection을 산출하는 새로운 모델이 등장했습니다.

최선의 선택의 전자 법칙 1/

모델의 본질은 삶이 순차적이고 현실 세계의 문제가 실시간으로 발생한다는 생각에 기반을 두고 있습니다.또한 특정 이벤트(지원자의 도착)가 발생할 특정 이벤트의 수에 대한 분포를 추정하는 것보다 더 자주 발생해야 하는 시간을 추정하는 것이 더 쉽습니다.이 아이디어는 다음과 같은 접근법, 이른바 통합 접근법(Unified Approach, 1984)으로 이어졌습니다.

모델은 다음과 같이 정의됩니다.순위가 매길 수 있는 지원자의$$ 알 수 없는 $숫자{\displaystyle }$N {\$displaystyle N}$ 중에서$$ 일정 시간 간격${\displaystyle }$[${\displaystyle 0,T]}${\$displaystyle [0,T]}$에서 지원자를 선택해야 합니다.목표는 서로 다른 순위의 모든 도착 순서가 동일할 가능성이 있다는 가설 하에서 가장 좋은 것만 선택할 확률을 최대화하는 것입니다.모든 지원자가${\displaystyle }$[${\displaystyle 0,}$ ${\displaystyle T]}$ ${\displaystyle [0,T]}$의 도착 시간 $밀도{\displaystyle }$ f ${\displaystyle f}$를 동일하지만 서로 독립적이라고 가정하고$$, F ${\displaystyle F}$가 해당 도착 시간 분포 함수를 나타내도록$$ 합니다. 즉,

${\displaystyle F}$( ${\displaystyle t}$ $=$ ${\displaystyle {}_{}^{}}$ 0 ${\displaystyle t_{}^{}}$ ${\displaystyle {}_{}^{}}$ (${\displaystyle }$s${\displaystyle }$) ${\displaystyle \mathrm{ds}}$ ${\displaystyle$)=\$int _{0}^{t}f(s)ds$ ${\displaystyle 0}$ ${\displaystyle \le }$ ${\displaystyle t}$ ${\displaystyle \le }$ ${\displaystyle T}$ ${\displaystyle \,0\leq t\leq$ T$}$입니다$.$

${\displaystyle$\tau } τ을 ${\displaystyle \mathrm{F}(}$τ${\displaystyle )}$ = 1 /${\displaystyle e}$라고 합니다${\displaystyle .}$ ${\displaystyle$ F$(\tau$) = $1$/ $e}$ τ까지 모든 지원자를 기다렸다가 관찰하는 전략을 고려하고$,$ 가능하면 이전의 모든 지원자보다 더 나은 ${\displaystyle$\tau } 시간 후 첫 번째 후보를 선택합니다.그렇다면 1/e-strategy라고 불리는 이 전략은 다음과 같은 속성을 가집니다.

1/e-전략

(i) $N개$의 모든 {\$displaystyle N}$에 대해 1/e 이상의 성공$$ 확률을 산출합니다.

$($ii) $N{\displaystyle }$ ${\displaystyle N}$을 모르는 선택자를 위한 최소 최대 최적 전략,

(iii) 신청자가 한 명 이상 있는 경우, 정확하게 1/e의 확률로 전혀 선택하지 않습니다.

1984년 F에 의해 증명된 1/e-law. 토마스 브루스, 깜짝 놀랄 일로 왔습니다.그 이유는 알려지지 않은 $N{\displaystyle }$ ${\displaystyle N}$의 모델에서는 이전에 약 1/e의 값이 도달할 수 없는 것으로 간주된 반면$,$ 이 값 1/e는 이제 성공 확률의 하한으로 달성되었으며, 이 값은 거의 틀림없이 가설이 훨씬 약한 모델에서 달성되었기 때문입니다(예:수학. 복습 85:m).

그러나, (i) 및 (ii)를 달성하는 다른 많은 전략들이 있으며, 더욱이 모든 $N{\displaystyle }$ ${\displaystyle N}$> 2에 대해 1/e-전략보다 동시에 더 나은 성능을 발휘합니다.간단한 예는 최소 한 명의 지원자가 이 시간 이전에 도착한 경우 시간 τ 후 첫 번째 $상대적$으로 가장 좋은 후보를 선택($가능$한 경우$)$하고, 그렇지 않은 경우 시간 τ 후 두 번째 상대적으로 가장 좋은 후보를 선택(가능한 경우$)$하는 전략입니다$.$

1/e-law는 숫자 1/e의 유사한 역할 때문에 위에서 설명한 고전적인 비서 문제의 해결책과 혼동되기도 합니다.그러나 1/e-law에서는 이 역할이 더 일반적입니다.또한 결과는 알려지지 않은 지원자 수를 유지하고 도착 시간 분포 F를 기반으로 한 모형이 지원자에게 더 다루기 쉽기 때문에 더 강력합니다.

구골놀이

"누가 비서 문제를 풀었는가?"(Ferguson, 1989)^[1]라는 기사에서 비서 문제는 1960년 2월 마틴 가드너의 "사이언티픽 아메리칸" 수학 게임 칼럼에 처음 등장했다고 합니다.

누군가에게 그가 원하는 만큼 많은 종이를 가져가라고 부탁하고, 각각의 종이에 다른 양수를 적으세요.숫자는 1의 작은 분수부터 구골 크기의 숫자(1 다음에 0이 100개 있음) 또는 그 이상의 범위에 이를 수 있습니다.이 전표들은 엎어져서 테이블 윗면에 걸쳐져 있습니다.한 번에 한 번씩, 당신은 그 전표들을 위로 향하게 합니다.목적은 시리즈 중 가장 큰 것으로 추측되는 숫자에 도달하면 회전을 멈추는 것입니다.다시 돌아가서 이전에 돌린 전표를 고를 수는 없습니다.전표를 모두 넘기면 당연히 마지막에 돌린 것을 골라야 합니다.^[4]

퍼거슨은 두 명의 적대적인 선수가 있는 제로섬 게임으로 비서 게임이 미해결 상태로 남아있다고 지적했습니다.^[1]이 게임에서:

• 정보가 있는 플레이어인 Alice는 $n개$의 ${\displaystyle n}$개의$$ 카드에 비밀스럽게 구별된 숫자를 씁니다.
• 멈춤 선수인 밥은 실제 값을 관찰하고 언제든 카드 돌리기를 멈출 수 있으며, 마지막으로 돌린 카드가 전체 최대 숫자를 가질 경우 승리합니다.
• Bob은 가능한 한 가장 높은 확률로 최대 수를 추측하고 싶어하지만 Alice의 목표는 이 확률을 가능한 낮게 유지하는 것입니다.

기본 비서 문제와의 차이점은 두 가지입니다.

• 앨리스는 무작위로 균일하게 숫자를 쓸 필요가 없습니다.그녀는 밥을 속이기 위해 어떤 공동 확률 분포에 따라 그것들을 쓸지도 모릅니다.
• Bob은 카드에 쓰인 실제 값을 관찰하고, 이 값을 자신의 결정 절차에 사용할 수 있습니다.

전략분석

앨리스는 먼저 n개의 숫자를 적고, 그 다음에 섞습니다.따라서 그들의 순서는 중요하지 않습니다. 즉, 앨리스의 숫자는 교환 가능한 랜덤 변수 시퀀스 $X{\displaystyle {}_{}}$ 1,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$, ${\displaystyle ...,X_{}}$ ${\displaystyle {}_{}}$ ${\$ ..., $X_{n}$이어야 합니다$.$ 앨리스의 전략은 가장 까다로운 교환 가능한 랜덤 변수 시퀀스를 선택하는 것입니다.

Bob의 전략은 X ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 2_{}}$ ${\displaystyle ...,X_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle X_{1}, X_{2$}, $..., X_{n}$ 시퀀스에 대한 정지 규칙 τ ${\displaystyle \tau}$로 형식화할 수 있습니다$.$

Bob에 대한 정지 규칙 τ ${\displaystyle \tau$}은$($는) 상대적 순위 ${\displaystyle {X1}_{}}$ ${\displaystyle {X2}_{}}$ ${\displaystyle ...,{Xn}_{}}$ ${\displaystyle X_{1}, X_{2$}, $..., X_{n},$및 숫자 값에 의존하지 않는 경우 상대적 순위 정지 전략이라고 합니다.즉, 마치 앨리스가 자신의 번호를 고른 후 누군가가 몰래 개입하여 ${\displaystyle {X1\mathrm{}}_{}}$ ${\displaystyle {X2\mathrm{}}_{}}$ ${\displaystyle ...,}$ ${\displaystyle {Xn}_{}}$ ${\$ ..., $X_{n}$의 각 번호를 상대 순위(무작위로 관계를 끊음)로$$ 변경한 것과 같습니다.예를 들어 $0{\displaystyle .2,}$ ${\displaystyle 0.3,}$ ${\displaystyle 0.3,}$ ${\displaystyle 0.1}$ ${\displaystyle 0.2, 0.3, 0.3, 0.1}$이(가$$) $동일$한${\displaystyle \mathrm{확률}}$로${\displaystyle 2,}$ ${\displaystyle 3}$,$$4, 1 {\$displaystyle 2$, $3,$ 4, 1${\displaystyle \}}$ ${\displaystyle \mathrm{또는}}$ ${\displaystyle 2,}$ ${\displaystyle 4}$, 3$,$ 1 {\$displaystyle 2,$ 4,$3,$ 3, 1}로$$ 변경됩니다.이렇게 하면 앨리스가 $\{{\displaystyle }$${\displaystyle 1,}$${\displaystyle 2,...,n\}}$ $\{\backslash {\displaystyle }$$displaystyle \{1,2,...,n\}${\displaystyle \{1${\displaystyle ,2,...,n\}}$ ${\displaystyle \{1,2,...,n\}$ $\{\backslash {\displaystyle }$displaystyle \{1,${\displaystyle 2,...,\mathrm{n<img\; alt="\{\backslash displaystyle\; \backslash \{1,2,...,n\backslash \}\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/d413a9d1a2271319b451a05b57d6a33d9420bb9c"\; style="vertical-align:\; -0.838ex;\; width:12.248ex;\; height:2.843ex;">}\}}$ ${\displaystyle \{1,2,...,n$최적 상대 순위 정지 전략은 위에서 주어진 비서 문제에 대한 최적 정지 규칙이며, 승리 확률이 있습니다.

그렇다면 앨리스의 목표는 밥이 상대적 순위의 멈춤 전략보다 더 잘할 수 없도록 하는 것입니다.

게임 규칙에 따라 앨리스의 시퀀스는 교환 가능해야 하지만 게임을 잘하기 위해서 앨리스는 독립적으로 선택해서는 안됩니다.Alice가 어떤 고정된 분포로부터 독립적으로 표본을 추출하면 Bob이 더 잘 할 수 있게 됩니다.이를 직관적으로 확인하려면 $n$ = ${\displaystyle 2}$ ${\displaystyle$n = $2$이고 Alice가 정규 $분포$ N${\displaystyle }$(${\displaystyle 0,}$ ${\displaystyle 1)}${\$displaystyle$ N ($0,$ 1$)}$에서$$두 숫자를 독립적으로 선택한다고 가정합니다.그런 다음 Bob이 한 숫자를 넘겨서${\displaystyle -3}$ ${\displaystyle -3}$을$($를) 본다면 두 번째 숫자를 자신 있게 넘길 수 있고, Bob이 한 숫자를 넘겨서 $+{\displaystyle 3}$ ${\displaystyle +3}$을(를) 본다면 첫 번째 숫자를 자신 있게 고를 수 있습니다$.$앨리스는 양의 상관 관계가 있는$$ X ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$을(를) 선택하여 더 잘 할 수 있습니다.

따라서 완전히 공식적인 진술은 다음과 같습니다.

임의의 정지 규칙 τ ${\displaystyle \tau }$에 대해 X${\displaystyle {}_{}{n}_{}}${\$displaystyle X_{1},..., X_{n}$의 교환 가능한 랜덤 변수 $시퀀스$가 있습니까$?$

$${\displaystyle Pr(X_{\tau }=\max _{i\in 1:n}X_{i})\leq \max _{r\in 1:n}{\frac {r-1}{n}}\sum _{i=r}^{n}{\frac {1}{i-1}}$$

?

해결책

$n$ = ${\displaystyle 2}$ ${\displaystyle$n = $2}$의 경우 Bob이 최적의 상대 순위 중지 전략을 수행하면 Bob이 이길 확률은 1/2입니다$.$놀랍게도, 앨리스는 미니맥스 전략이 없는데, 이것은 T. 커버의^[5] 역설과 두 봉투의 역설과 밀접한 관련이 있습니다.구체적으로, Bob은 임의의 숫자 $Y{\displaystyle }$ ${\displaystyle Y}$를 샘플링하는 전략을 구사할 수 있습니다$.$ 만약 X > ${\displaystyle X_{1}$ >$Y}$을를$)$ ${\displaystyle {선택}_{}}$한 $다음{\displaystyle {}_{}}$ X 1 {\displaystyle $X_{1}}$을$($를) 선택한 다음 $X{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$을(를) 선택합니다$.$ 이제 Bob은 1/2보다 엄격하게 큰 확률로 이길 수 있습니다.앨리스의 숫자가 다르다면 $Y$ ∉에 조건부${\displaystyle }$[${\displaystyle min}$ (${\displaystyle }$X ${\displaystyle 1_{}}$ X ${\displaystyle 2_{}}$),${\displaystyle max}$( ${\displaystyle {}_{}}$ ${\displaystyle 1_{}}$ X ${\displaystyle 2_{}}$)${\displaystyle }$] ${\displaystyle Y\not \in [\min(X_{1}, X_{2}),\max(X_{1}, X_{2})},$Bob은 확률 1/2로 이기지만 $Y$ ∈에 조건부 ${\displaystyle [min}$ (${\displaystyle {}_{}}$ ${\displaystyle 1_{}}$ X ${\displaystyle 2_{}),}$ ${\displaystyle max}$( ${\displaystyle {}_{}}$ ${\displaystyle 1_{}{}_{}}$ X ${\displaystyle {}_{}}$)${\displaystyle }$] ${\displaystyle Y\in [\min(X_1}, X_{2}),\max(X_{1}, X_{2}},$Bob은 확률 1/2로 이기며,ility 1.

난수 $Y$ ${\displaystyle Y}$는 $Y$ ∈ ${\displaystyle [min({X1}_{}}$ ${\displaystyle {X2}_{}),}$ ${\displaystyle max}$(${\displaystyle {X1}_{}}$ ${\displaystyle Y\in [\min(X_{1}, X_{2}),\max(X_{1}, X_{2}]}$이(가) 0이 아닌 확률이면 임의 분포에서 샘플링할 수 있습니다.

그러나ϵ> 0 {\$displaystyle$ \epsilon >$0}$에대해 앨리스는 Bob의 승리 확률이 최대 $1{\displaystyle /2}$ +${\displaystyle }$ϵ ${\displaystyle 1/2 +\epsilon$}이$($${\displaystyle {가}_{}}$) 되도록 교환 가능한 시퀀스 ${\displaystyle X_{}}$ 1${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$2 {\$displaystyle X_{1}, X_{2}}$을(를) 구성할 수 있습니다$.$

그러나 > ${\displaystyle n>2}$의 경우 대답은 yes입니다앨리스는 Bob이 상대적 순위를 기반으로 고전적인 중지 전략을 사용하는 것보다 더 잘 놀 수 없는 방식으로 난수(의존적 난수 변수)를 선택할 수 있습니다.^[6]

휴리스틱 성능

기사의 나머지 부분은 알려진 지원자 수의 비서 문제를 다시 다루고 있습니다.

Stein, Seale & Rapoport 2003은 비서 문제에 사용될 수 있는 심리적으로 그럴듯한 휴리스틱에 대한 예상 성공 확률을 도출했습니다.그들이 조사한 휴리스틱은 다음과 같습니다.

• 컷오프 규칙(CR): 첫 번째 y명의 지원자 중 어느 누구도 수락하지 마십시오. 그 후, 첫 번째로 조우한 지원자(즉, 상대 순위 1위의 지원자)를 선택합니다.이 규칙은 y = r인 고전적인 비서 문제에 대한 최적의 정책을 특별한 경우로 가지고 있습니다.
• 후보 카운트 규칙(CCR): y번째 후보를 선택합니다.참고로, 이 규칙은 반드시 지원자를 건너뛰는 것은 아니며, 지원자 순서에서 의사결정자가 얼마나 깊은지는 고려하지 않고, 얼마나 많은 지원자가 관찰되었는지만 고려합니다.
• 연속 비후보 규칙(SNCR): y명의 비후보자(즉, 상대적 순위가 1위인 지원자)를 관찰한 후 첫 번째로 조우한 후보자를 선택합니다.

각 휴리스틱에는 단일 매개변수가 있습니다.그림(오른쪽 shown)은 n = 80의 문제에 대한 y의 함수로 각 휴리스틱에 대한 예상 성공 확률을 표시합니다.

기본 보수 변형

한 명의 최고 지원자를 찾는 것은 다소 엄격한 목표처럼 보일 수 있습니다.면접관은 낮은 평가를 받는 지원자보다 높은 평가를 받는 지원자를 채용하고, 최고를 얻는 것에만 관심을 가질 것이라고 상상할 수 있습니다.즉, 면접관은 반드시 최고가 아닌 지원자를 선택함으로써 어느 정도의 가치를 도출하고, 도출된 가치는 선택된 한 명의 가치에 따라 증가합니다.

이 문제를 모형화하려면 ${\displaystyle n}$의 지원자가 [0, 1]의 균일한 분포에서 추출한 랜덤 변수 X인 "true" 값을 갖는다고 가정합니다.앞서 설명한 고전적인 문제와 유사하게 면접관은 각 지원자가 지금까지 최고인지(지원자)만 관찰하고, 현장에서 각 지원자를 합격 또는 불합격시켜야 하며, 도달한 경우에는 마지막 지원자를 합격시켜야 합니다(분명히 말하면 면접관은 각 지원자의 실제 상대적 서열을 배우지 않습니다).지원자의 상대적 서열 1위 여부만 학습합니다.그러나 이 버전에서는 선택한 지원자의 실제 값에 의해 보상이 제공됩니다.예를 들어, 지원자가 참값이 0.8인 지원자를 선택하면 0.8이 됩니다.면접관의 목표는 선발된 지원자의 기대 가치를 극대화하는 것입니다.

지원자의 값은 [0, 1]의 균일한 분포로부터 i.i.d. 도면이므로, $x$ ${\displaystyle t_{}}$ = ${\displaystyle max}${ x ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 2_{}}$ ${\displaystyle \dots ,}$x ${\displaystyle t_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle x_{t$}=\$max \left\{x_{1}, x_{2},\ldots, x_{t}\right\}$가 주어집니다.

${\displaystyle E_{t}=E\left(X_{t} I_{t}=1\right)={\frac {t}{t+1}}}$

고전적 문제에서와 같이 최적의 정책은 임계값에 의해 제공되며, 이 문제에 대해 면접관이 후보자를 수락하기 시작해야 $하는$c ${\displaystyle$ c$}$로 표시됩니다.Bearden은 c가 ⌊ ${\displaystyle n}$ ⌋${\displaystyle \lfloor${\sqrt {$n}}\rfoor}$ ${\displaystyle 또는}$ ⌈ n ⌉$$\$lceil${\$sqrt {n}\rceil}$임을 보여주었습니다$.$ (사실, $n$ ${\displaystyle {\sqrt {n}}$에 가장 가까운 것 중 하나입니다.)이는 $n개$의 ${\displaystyle n}$개의$$ 지원자에 문제가 발생했을 때 일부 임의 임계값 $1{\displaystyle \mathrm{}}$ ${\displaystyle \le }$ ${\displaystyle c}$ ${\displaystyle \le }$ ${\displaystyle n}$ ${\displaystyle 1\leq c\leq n}$에 대한 예상 보상이$$

${\displaystyle V_{n}(c)=\sum _{t=c}^{n-1}\left[\prod_{s=c}^{t-1}\left]\frac {s-1}{s}\right)\right]\left]\left ({\frac {1}{t+1}\right)+\left[\prod_{s=c}^{n-1}\left ({\frac {s-1}{s}\right)\right]{\frac {1}{2}}={\frac {2cn-{c}^{2}+c-n}{2cn}}}.$

${\displaystyle {vn}_{}}$ (${\displaystyle {}_{}c}$) ${\displaystyle V_{n}(c)}$을(를) c로 구별하면 다음을 얻을 수 있습니다.

${\displaystyle {\frac {\partial V}{\partial c}}={\frac {-{c}^{\,2}+n}{2{c}^{\,2}n}}}.$

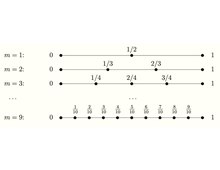
$c$ ${\displaystyle c}$의 모든 허용 값에 대해 ∂ /∂ < 0 ${\displaystyle \$partial ^{,$2}V/\partial$ c$^{,2}<0}$이므로$$V ${\displaystyle$ V$}$는 ${\displaystyle c}$ = n ${\displaystyle$c = {\$sqrt {n}}$에서 최대화됩니다$.$ V는 $c$ ${\displaystyle c}$에서 볼록하므로 최적 정수 값 임계값은$$⌊ ${\displaystyle n}$ ⌋ ${\displaystyle \lfloor {\sqrt {n}$이어야 합니다.$\rfloor}$ 또는 $⌈$ ${\displaystyle n}$ $⌉$ ${\displaystyle} \lceil {\$sqrt {$n}}\rceil}.$ $따라서$$$n ${\displaystyle$ n$}$의 대부분의 값에 대해 면접관은 단일 최고 지원자를 선택하는 것이 목표인 고전 버전보다 기본 보수 버전에서 지원자를 더 빨리 받기 시작합니다.이는 점근적 결과가 아닙니다.$n개$의$$모든 {\$displaystyle n}$에 대해 유지되지만 알려진 분포에서 예상되는 값을 최대화하는 데 최적의 정책이 아닙니다$.$알려진 분포의 경우, 동적 프로그래밍을 통해 최적의 플레이를 계산할 수 있습니다.

Palley and Kremer(2014)^[8]가 도입한 이 문제의 보다 일반적인 형태는 각 신규 지원자가 도착할 때 면접관이 이전에 관찰한 모든 지원자에 대한 순위를 관찰한다고 가정합니다.이 모델은 면접관이 도착했을 때 새로운 후보를 평가하기 위해 사용할 수 있는 일련의 과거 데이터 포인트를 축적함으로써 그들이 탐색 과정을 계속하면서 학습한다는 개념과 일치합니다.소위 부분 정보 모델의 이점은 면접관이 각 지원자의 가치에 대한 완전한 정보를 제공받은 경우 상대적인 순위 정보가 주어졌을 때 달성된 결정 및 결과를 해당하는 최적의 결정 및 결과와 직접 비교할 수 있다는 것입니다.지원자가 알려진 분포로부터 독립적으로 추첨되고 면접관이 선정된 지원자의 기대 가치를 극대화하기 위해 노력하는 이 완전 정보 문제는 원래 Moser(1956),^[9] Sakaguchi(1961),^[10] Karlin(1962)에 의해 해결되었습니다.

기타 수정사항

비서 문제에는 단순하고 우아한 해결책도 있는 여러 가지 변형이 있습니다.

한 번의 시도로 차선책을 선택합니다.

한 가지 변형은 가장 좋은 것을 선택하려는 욕구를 두 번째로 좋은 것을 선택하려는 욕구로 대체합니다.^[11][12][13]로버트 J. 밴더베이는 이것을 "포스트닥" 문제라고 부르며, "최고"는 하버드 대학에 갈 것이라고 주장합니다.이 문제의 경우 짝수 지원자의 성공 확률은 정확히 $0{\displaystyle \frac{\mathrm{.}{}^{}}{(n}}$- ${\displaystyle \frac{1)}{}}$ ${\$입니다$.$ 이 확률은 n이 차선보다 최선을 선택하기 쉽다는 사실을 나타내는 무한대의 경향이 있으므로 1/4 경향이 있습니다.

발차기를 이용해서 제일 좋은 것을 고르세요.

k개의 후보 중에서 k개의 최고 비서를 뽑는 문제를 고려해보세요.

일반적으로 최적의 결정 방법은 $r{\displaystyle }$=${\displaystyle }$⌊ ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{ke1}^{}}{}}$ / k ⌋ {\$displaystyle$ r =\$left\l$ floor ${\frac {n}{$ke$^{1/$k}}\$right\rfloor }$개의 후보를 하나도 선택하지 않고 관찰한 후, 후보가 부족하거나 선택할 때까지 첫 $번째$ r개의 ${\displaystyle$ r$}$개의 후보보다 우수한 모든 후보를 선택합니다.$k$ ${\displaystyle k}$이(가) 일정하게 유지되고${\displaystyle }$n${\displaystyle \mathrm{}}$→$$∞ {\$displaystyle$n\$to$ \infty$}$인 경우$$성공 확률은 $1$ ${\displaystyle \frac{\mathrm{ek}}{}}$ ${\frac {1}{ek}}$로 수렴됩니다$.$ Vanderbe 1980에서 $k$ = ${\displaystyle n}$/ 2 ${\displaystyle$k=$n/2}$인 경우$$성공 확률은 1 ${\displaystyle \frac{n}{}}$/ ${\displaystyle \frac{2}{}}$+ ${\displaystyle \frac{1}{}}$ ${\frac {1}{n/2+1}}$입니다$.$

여러 번 시도하여 최상의 것을 고릅니다.

이 변형에서는 플레이어에게 $r{\displaystyle }$ ${\displaystyle r}$개의 선택이$$ 허용되며, 어떤 선택이 최선일 경우 승리합니다.이 문제에 대한 최적의 전략은 임계값 집합$({\displaystyle {}_{}}$ ${\displaystyle 1_{}}$ a ${\displaystyle 2_{}}$ ${\displaystyle ...,}$ ${\displaystyle r_{}}$)${\displaystyle (a_{1}, a_{2$}, $..., a_{r})}$로 정의된 전략 클래스에 속합니다 여기서 a > a >⋯ > ${\displaystyle a_{1}> a_{2}>\cdots$> $a_{r}}.$

구체적으로$,$ $1{\displaystyle \mathrm{}}$ {\$displaystyle 1}$부터 r ${\displaystyle$ r$}$까지의 ${\displaystyle r}$의 수락 문자가$$ 있다고 가정합니다$.$ 각각 하나의 문자를 보유한 ${\displaystyle r}$의 응용 프로그램 담당자가 있다고 가정합니다.후보자들을 계속 인터뷰해서 모든 지원 담당자들이 볼 수 있는 차트에 순위를 매깁니다.이제 $i{\displaystyle }$ ${\displaystyle i}$ 장교가 모든$$ $후보자{\displaystyle \mathrm{}}$ 1 ${\displaystyle 1}$보다 우수한 첫 번째 후보자에게 ${\displaystyle {합격}_{}}$통지서를 i {\$displaystyle$ a_{$i}}$에게 보냅니다$.$ (미전송 합격 통지서는 기본적으로 최종 지원자에게 주어지는데, 이는 표준 비서 문제와 동일합니다.)^[15]

$n$ → ∞ ${\displaystyle n\rightarrow \infty}$ 제한에서, 각 ${\displaystyle {ai}_{}}$~ ${\displaystyle {}^{}}$- ${\displaystyle {{ki}_{}}^{}}${\$displaystyle a_{i}\sim$ ne$^{-k_{i$ 일부 $유리수$ ${\displaystyle {ki}_{}}${\$displaystyle k_$에 대하여.

이길 확률

$r$ = ${\displaystyle 2}$ ${\displaystyle$r=$2}$일 때$,$ 이길 $확률$은 e${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$+ ${\displaystyle {}^{}}$ -${\displaystyle 3^{}}$ ${\displaystyle {\frac{2}{}}^{},}$ (${\displaystyle n}$ → ∞${\displaystyle }$) ${\displaystyle e^{-1}$ + e$^{-{\frac {3}{2}},$ ($n\rightarrow$ \$infty$ $)\}.$ 보다 일반적으로 $양$의 정수$$r {\$displaystyle r}$일 때,$$이길 $확률$은 p${\displaystyle {}_{}}$1 + ${\displaystyle p_{}}$ 2${\displaystyle {}_{}}$+${\displaystyle }$⋯ + ${\displaystyle p_{}}$r {\$displaystyle p_1}$ + $p_{2$} $+\cdots + p_{r$},$$여기서 ${\displaystyle {pi}_{}}$ = ${\displaystyle \underset{}{lim}}$ n${\displaystyle \underset{}{\to }}$∞ ${\displaystyle p_{i$ ${n\rightarrow \infty}}{\frac {a_{i}}{n$의 ${\displaystyle \frac{a_{}}{}}$입니다.

^[15] ${\displaystyle {\mathrm{e}}^{}}$- $1{\displaystyle }$+ ${\displaystyle {}^{}}$-$$3 2 + e - $47$ 24 +$e$${\displaystyle {}^{}}$-$$${\displaystyle {\frac{2761}{}}^{}}$ ${\displaystyle {\frac{1152}{}}^{}}${\$displaystyle e$$1}$ +$e^{\frac {3}{2}}}$ + $e^{-{\frac${47$}{24}}$ + $e^{-{\frac {2761}{1152}}}$까지 계산됩니다$.$

Matsui & Ano 2016은 일반적인 알고리즘을 제공했습니다.예를 들어 ${\displaystyle {p5}_{}}$ = ${\displaystyle {}^{}}$ -${\displaystyle {\frac{4162637}{}}^{}}$ ${\displaystyle {\frac{1474560}{}}^{}}$ ${\displaystyle p_{5$ = e$^{-{\frac {4162637}{1474560}}}.$

실험연구

실험심리학자와 경제학자들은 비서 문제 상황에서 실제 사람들의 의사결정 행동을 연구했습니다.^[17]대부분의 경우, 이 연구는 사람들이 너무 빨리 검색을 중단하는 경향이 있다는 것을 보여주었습니다.이것은 적어도 부분적으로 후보자들을 평가하는 비용에 의해서 설명될 수 있습니다.실제 환경에서는 의사결정 대안이 순차적으로 발생하는 문제에 직면할 때마다 사람들이 충분히 검색하지 않는다는 것을 의미할 수 있습니다.예를 들어, 고속도로를 따라 어느 주유소에 주유소를 세울지 결정하려고 할 때, 사람들은 주유소를 멈추기 전에 충분히 검색하지 못할 수도 있습니다.만약 사실이라면, 그들은 더 오래 검색했을 때보다 기름값을 더 지불하는 경향이 있을 것입니다.사람들이 온라인으로 항공권을 검색할 때도 마찬가지일 것입니다.비서 문제와 같은 문제에 대한 실험적 연구를 행동 운영 연구라고 부르기도 합니다.

신경상관관계

동물과^[18][19] 인간 모두를 사용하는 지각적 의사 결정 작업에서 정보 통합 또는 신념의 표현에 대한 상당한 신경과학 연구가 있지만, 정보 수집을 중단하는 결정이 어떻게 도달하는지에 대해서는 상대적으로 거의 알려져 있지 않습니다.^[20]

연구자들은 기능성 MRI를 사용하여 건강한 지원자들의 비서 문제를 해결하는 신경 기초를 연구했습니다.^[21] 마르코프 의사 결정 과정(MDP)을 사용하여 검색을 계속하는 것과 현재 옵션을 약속하는 것의 값을 정량화했습니다.선택지를 선택하는 것과 거부하는 것을 결정하는 것은 두정 및 배측 전전두피질, 복측 선조체, 전방 절연체 및 전방 천자와 관련이 있습니다.따라서 이전에 증거 통합 및 보상 표현과 관련된 뇌 영역은 선택에 대한 결정을 유발하는 임계 교차를 인코딩합니다.

역사

비서 문제는 1949년 메릴 M에 의해 도입된 것으로 보입니다. 그 해 강연에서 약혼녀 문제라고 불렀던 플러드.그는 1950년대에 여러 차례 언급했는데, 예를 들어 1958년 5월 9일 퍼듀에서 열린 컨퍼런스 강연에서 이를 언급했고, 그 당시 아무 것도 출판되지 않았지만 결국 민속학에 널리 알려지게 되었습니다.1958년에 그는 레너드 길먼에게 편지를 보내 새뮤얼 칼린과 J. 로빈스를 포함한 12명의 친구들에게 최적의 전략을 설명하고 R. 팔레르모의 부록과 함께 모든 전략은 "첫 번째 p를 무조건 거부하고 다음에 더 나은 후보를 받아들인다"는 형식의 전략에 의해 지배된다는 것을 증명하는 편지를 보냈습니다.^[22]

첫번째 출판물은 1960년 2월 사이언티픽 아메리칸에 마틴 가드너에 의해 출판되었습니다.그는 존 H. 폭스 주니어와 L. 제럴드 마니로부터 그것에 대해 들은 적이 있는데, 그들은 1958년에 이와 동등한 문제를 독자적으로 생각해 냈습니다. 그들은 그것을 "구골의 게임"이라고 불렀습니다.Fox와 Marnie는 최적의 해결책을 알지 못했습니다. Gardner는 J. R. Founder와 함께 잡지에 게재하기 위해 정확한 분석을 제공한 Leo Moser에게 조언을 구했습니다.얼마 지나지 않아 몇몇 수학자들이 가드너에게 편지를 보내 그들이 포도나무를 통해 들었던 것과 같은 문제에 대해 이야기했는데, 이 모든 것들은 아마도 플러드의 원작으로 거슬러 올라갈 수 있습니다.^[23]

최선의 선택을 할 수 있는 1/e-law는 F에 기인합니다. 토마스 브루스.^[24]

퍼거슨은 광범위한 참고 문헌을 보유하고 있으며, 1875년 아서 케일리에 의해서도, 심지어 그 훨씬 전인 1611년(1613년), 첫 번째 부인이 사망한 후 2년 동안 11명의 결혼 후보자를 조사하는 데 시간을 보낸 요하네스 케플러에 의해서도 유사한 (그러나 다른) 문제가 고려되었다고 지적하고 있습니다.^[25]

조합 일반화

비서 문제는 다양한 직무가 여러 개 존재하는 경우로 일반화할 수 있습니다.역시 무작위 순서로 들어오는 지원자가$$ ${\displaystyle n}$입니다.후보자가 도착하면 음수가 아닌 숫자의 집합이 나타납니다.각 값은 작업 중 하나에 대한 그녀의 자격을 지정합니다.관리자는 지원자를 데려갈지 말지 결정해야 할 뿐만 아니라, 만약 그렇다면 그녀를 한 일에 영구적으로 배치해야 합니다.목표는 자격 요건의 합이 최대한 큰 과제를 찾는 것입니다.이 문제는 한 변의 $n개$의$${\$displaystyle n}$개$$ 노드가 무작위 순서로 온라인에 도착하는 에지 가중치 이중 그래프에서 최대 가중치 일치를 찾는 것과 동일합니다.따라서 온라인 초당 매칭 문제의 특별한 경우입니다.

비서 문제에 대한 고전적인 알고리즘을 일반화함으로써, 예상되는 자격의 합이 최적(오프라인) 할당보다 작은$$ ${\displaystyle$ e$}$의 인자일 뿐인 할당을 얻을 수 있습니다.^[26]

참고 항목

• 과제문제
• 오즈 알고리즘
• 최적정지
• 로빈스의 문제
• 탐색이론
• 안정적인 결혼문제

메모들

참고문헌

• Bearden, J.N. (2006). "A new secretary problem with rank-based selection and cardinal payoffs". Journal of Mathematical Psychology. 50: 58–9. doi:10.1016/j.jmp.2005.11.003.
• Bearden, J.N.; Murphy, R.O.; Rapoport, A. (2005). "A multi-attribute extension of the secretary problem: Theory and experiments". Journal of Mathematical Psychology. 49 (5): 410–425. CiteSeerX 10.1.1.497.6468. doi:10.1016/j.jmp.2005.08.002. S2CID 9186039.
• Bearden, J. Neil; Rapoport, Amnon; Murphy, Ryan O. (September 2006). "Sequential Observation and Selection with Rank-Dependent Payoffs: An Experimental Study". Management Science. 52 (9): 1437–1449. doi:10.1287/mnsc.1060.0535.
• Bruss, F. Thomas (June 2000). "Sum the odds to one and stop". The Annals of Probability. 28 (3): 1384–1391. doi:10.1214/aop/1019160340.
• Bruss, F. Thomas (October 2003). "A note on bounds for the odds theorem of optimal stopping". The Annals of Probability. 31 (4): 1859–1961. doi:10.1214/aop/1068646368.
• Bruss, F. Thomas (August 1984). "A Unified Approach to a Class of Best Choice Problems with an Unknown Number of Options". The Annals of Probability. 12 (3): 882–889. doi:10.1214/aop/1176993237.
• Flood, Merrill R. (1958). "Proof of the optimum strategy". Letter to Martin Gardner. Martin Gardner papers series 1, box 5, folder 19: Stanford University Archives.{{cite press release}}: CS1 메인 : 위치 (링크)
• Freeman, P.R. (1983). "The secretary problem and its extensions: A review". International Statistical Review / Revue Internationale de Statistique. 51 (2): 189–206. doi:10.2307/1402748. JSTOR 1402748.
• Gardner, Martin (1966). "3". New Mathematical Diversions from Scientific American. Simon and Schuster. [1960년 2월 출간된 자신의 칼럼을 추가 논평과 함께 재인쇄]
• Girdhar, Yogesh; Dudek, Gregory (2009). "Optimal Online Data Sampling or How to Hire the Best Secretaries". 2009 Canadian Conference on Computer and Robot Vision. pp. 292–298. CiteSeerX 10.1.1.161.41. doi:10.1109/CRV.2009.30. ISBN 978-1-4244-4211-9. S2CID 2742443.
• Gilbert, J; Mosteller, F (1966). "Recognizing the Maximum of a Sequence". Journal of the American Statistical Association. 61 (313): 35–73. doi:10.2307/2283044. JSTOR 2283044.
• Gnedin, A. (1994). "A solution to the game of Googol". Annals of Probability. 22 (3): 1588–1595. doi:10.1214/aop/1176988613.
• Gnedin, A. (2021). "The best choice problem with random arrivals: How to beat the 1/e-strategy". Stochastic Processes and Their Applications. 145: 226–240. doi:10.1016/j.spa.2021.12.008. S2CID 245449000.
• 힐, T.P. "멈춰야 할 때를 알고 있습니다."미국 과학자, Vol. 97, 126-133 (2009)(프랑스어 번역은 Pourla Science(2009) 7월호 커버스토리 참조)
• Ketelaar, Timothy; Todd, Peter M. (2001). "Framing Our Thoughts: Ecological Rationality as Evolutionary Psychology's Answer to the Frame Problem". Conceptual Challenges in Evolutionary Psychology. Studies in Cognitive Systems. Vol. 27. pp. 179–211. doi:10.1007/978-94-010-0618-7_7. ISBN 978-94-010-3890-4.
• Matsui, T; Ano, K (2016). "Lower bounds for Bruss' odds problem with multiple stoppings". Mathematics of Operations Research. 41 (2): 700–714. arXiv:1204.5537. doi:10.1287/moor.2015.0748. S2CID 31778896.
• Miller, Geoffrey F. (2001). The mating mind: how sexual choice shaped the evolution of human nature. Anchor Books. ISBN 978-0-385-49517-2.
• Sardelis, Dimitris A.; Valahas, Theodoros M. (March 1999). "Decision Making: A Golden Rule". The American Mathematical Monthly. 106 (3): 215. doi:10.2307/2589677. JSTOR 2589677.
• Seale, D.A.; Rapoport, A. (1997). "Sequential decision making with relative ranks: An experimental investigation of the 'secretary problem'". Organizational Behavior and Human Decision Processes. 69 (3): 221–236. doi:10.1006/obhd.1997.2683.
• Stein, W.E.; Seale, D.A.; Rapoport, A. (2003). "Analysis of heuristic solutions to the best choice problem". European Journal of Operational Research. 151: 140–152. doi:10.1016/S0377-2217(02)00601-X.
• Vanderbei, R. J. (November 1980). "The Optimal Choice of a Subset of a Population". Mathematics of Operations Research. 5 (4): 481–486. doi:10.1287/moor.5.4.481.
• Vanderbei, Robert J. (2012). "The postdoc variant of the secretary problem" (PDF). CiteSeerX 10.1.1.366.1718. {{cite journal}}:저널 요구사항 인용 journal=(도움말)

외부 링크

• OEIS sequence A054404 (n명의 딸과 술탄의 지참금 문제를 선택하기 전에 대기할 딸의 수)
• Weisstein, Eric W. "Sultan's Dowry Problem". MathWorld.
• Neil Bearden. "Optimal Search (Secretary Problems)". Archived from the original on 4 January 2017.
• Thomas S의 Optimal Stoping and Applications book퍼거슨

메모들