별의 맥동

이 문서에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 본 기사 또는 섹션은 검증할 수 있는 주요 주제를 언급하거나 관련되지 않은 자료의 합성을 포함할 수 있다. 관련 토론은 토크 페이지에서 확인할 수 있습니다.(2010년 9월) (이 템플릿메시지의 삭제 방법과 삭제 타이밍을 확인) 이 글은 위키피디아 편집자의 개인적인 감정을 기술하거나 주제에 대한 독창적인 주장을 제시하는 개인적인 성찰, 개인적인 에세이 또는 논쟁적인 에세이처럼 쓰여집니다. 백과사전 형식으로 다시 작성하여 개선하시기 바랍니다. (2010년 9월) (이 템플릿메시지의 삭제 방법과 삭제 타이밍에 대해 알아보기) 이 기사의 주요 기고자는 그 주제와 밀접한 관련이 있는 것으로 보인다.Wikipedia의 콘텐츠 정책, 특히 중립적인 관점을 준수하기 위해 청소가 필요할 수 있습니다.토크 페이지에서 더 자세히 논의해 주세요. (2010년 9월)(이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

별의 맥동은 별이 평형을 유지하려고 할 때 외부 층의 팽창과 수축에 의해 발생합니다.별의 반지름의 이러한 변동은 별의 광도에 상응하는 변화를 일으킵니다.천문학자들은 스펙트럼을 측정하고 도플러 ^[1]효과를 관찰함으로써 이 메커니즘을 추론할 수 있다.고전적인 세페이드, 거문고자리 RR 별, 진폭이 큰 방패자리 델타 별과 같이 큰 진폭으로 맥동하는 많은 고유 변광성들은 규칙적인 광도 곡선을 보인다.

이러한 규칙적인 행동은 헤르츠스프룽-러셀 도표에서 고전적 변광성의 고휘도/저온 쪽에 평행하게 놓여 있는 별의 변동성과 대조적이다.이들 거성은 약한 불규칙성부터 (대부분의 황소자리 RV 및 반규칙 변광성과 같이) 평균 주기 시간 또는 주기를 정의할 수 있는 경우 불규칙 변광성에 거의 반복성이 없는 경우까지 다양한 맥동을 겪는 것으로 관측된다.짧은 주기는 규칙적이고 긴 주기는 먼저 맥동 주기에서 비교적 규칙적인 변화를 보이고, 그 후 RV 황소자리 별에서와 같이 경미한 불규칙성이 나타나며, 그 ^[2][3]주기가 길어짐에 따라 서서히 변형을 일으킨다.별의 진화와 맥동 이론에 따르면 이 불규칙한 별들은 광도 대 질량(L/M) 비율이 훨씬 더 높습니다.

많은 별들은 비방사성 맥동성으로, 표준 ^[4][5]초로 사용되는 일반 변수보다 밝기 변동이 작습니다.

정규 변수

불규칙한 변동성의 전제조건은 별이 일정 주기의 시간 척도에 따라 진폭을 변경할 수 있어야 한다는 것입니다.즉, 맥동과 열 흐름 사이의 결합은 그러한 변화를 허용하기에 충분히 커야 한다.이 결합은 하나의 맥동 주기(주기)에서 주어진 정상 모드의 진폭에 대한 상대적 선형 성장 또는 붕괴 속도 θ(kappa)로 측정된다.정규 변수(Cepheids, RR Lyrae 등)의 경우, 수치적 항성 모델링과 선형 안정성 분석 결과 δ는 관련되고 들뜬 맥동 모드에 대해 최대 2%의 차수를 보인다.한편, 같은 타입의 분석에서는, L/M이 높은 모델에서는, δ가 상당히 큰(30%이상) 것을 알 수 있다.

정규 변수의 경우 상대 성장률이 작다는 것은 두 가지 뚜렷한 시간 척도, 즉 진동 주기와 진폭 변동과 관련된 더 긴 시간이 있음을 의미합니다.수학적으로 말하면, 역학에는 중심 다지관, 더 정확히 말하면 근중심 다지관이 있습니다.게다가 별의 맥동은 그 설명이 맥동 진폭의 제한적인 힘일 수 있다는 점에서 약하게 비선형적이라는 것이 밝혀졌습니다.이 두 가지 특성은 매우 일반적이며 인구 역학, 해양학, 플라즈마 물리학 등과 같은 많은 다른 분야의 진동계에서 발생합니다.

약한 비선형성과 진폭 변동의 긴 시간 척도는 맥동 시스템의 시간적 설명을 맥동 진폭의 시간적 설명으로만 단순화함으로써 주기의 짧은 시간 척도의 움직임을 제거할 수 있습니다.그 결과 진폭의 낮은 전력으로 잘린 진폭 방정식의 관점에서 시스템을 설명합니다.그러한 진폭 방정식은 다양한 기법에 의해 도출되었다. 예를 들어, 세속적인 항을 제거하는 푸앵카레-린드스테트 방법이나 다시간 점근 섭동 방법,^[6][7][8] 그리고 보다 일반적으로 정규 형태 ^[9][10][11]이론이다.

예를 들어, 두 개의 비공진 모드의 경우, RR Lyrae 변수에서 일반적으로 발생하는 상황, 두 개의 정규 모드 1과 2의 진폭₁ A와₂ A의 시간적 진화는 다음과 같은 일련의 상미분 방정식에 의해 제어된다.

${\displaystyle dA_{1}/dt=\kappa_{1}+(Q_{11}A_{1}^{2}+Q_{12}A_{2}^{2}A_{1}}$

${\displaystyle dA_{2}/dt=\kappa_{2}A_{2}+(Q_{21)A_{1}^{2}+Q_{22}A_{2}^{2}A_{2}}:$

여기서 Q는_ij 비공진 결합 ^[12][13]계수입니다.

이러한 진폭 방정식은 가장 낮은 차수의 중요하지 않은 비선형성으로 제한되었습니다.항성 맥동 이론에서 관심 있는 해법은 (시간이 무한대로 가는 경향이 있기 때문에) 점근해이다. 왜냐하면 진폭 변동에 대한 시간 척도는 핵 연소 시간 척도인 별의 진화 시간 척도에 비해 일반적으로 매우 짧기 때문이다.위의 방정식에는 단일 모드(A₁ ${\$ \$displaystyle \neq$} 0$$, A₂₁₂$$= 0) 또는 이중 모드₁(A$$ \$displaystyle \neq$$$} 0$$$,$ A ≠ \$display$style \$neq$ } 0, A${\displaystyle }$≠ \$display$style \$neq$$$} 0₂)에 대응하는 일정한 진폭을 갖는 고정 소수점 솔루션이 있습니다.이것은 별의 단일 주기 및 이중 주기 맥동에 해당합니다.물리적(즉, 음) 결합 계수에 대해 위의 방정식의 다른 점근적 해법이 존재하지 않는다는 것을 강조하는 것이 중요하다.

공진 모드의 경우 적절한 진폭 방정식에는 모드 간의 공진 커플링을 설명하는 추가 항이 있습니다.고전적인 (단일 주기적인) 세페이드들의 광곡선 형태학에서 헤르츠스프룽 진행은 기본 맥동 모드와 두 번째 오버톤 ^[14]모드 사이에서 잘 알려진 2:1 공명의 결과이다.진폭 방정식은 비방사성 항성 ^[15][16]맥동까지 확장될 수 있습니다.

맥동별의 전체 분석에서 진폭 방정식은 가능한 맥동 상태 사이의 분기도를 매핑할 수 있도록 합니다.이 그림에서 별의 진화 과정에서 맥동이 시작되는 불안정 띠의 경계는 ^[17]홉 분기점에 해당합니다.

중심 다지관의 존재는 주기의 시간 척도에서 혼돈(즉, 불규칙) 맥동의 가능성을 제거한다.공명진폭방정식은 혼돈해결을 허용하기에 충분히 복잡하지만, 이는 진폭의 시간적 변동에 있고 긴 시간 척도로 발생하기 때문에 매우 다른 혼돈입니다.

진폭 방정식이 적용될 때 맥동 진폭의 시간적 변화에서 장기간 불규칙한 동작이 가능하지만, 일반적인 상황은 아닙니다.실제로, 대부분의 관측과 모델링에서, 이러한 별들의 맥동은 일정한 푸리에 진폭으로 발생하며, 주기적 또는 다주기적(수리 문헌에서 준주기적)일 수 있습니다.

불규칙한 맥동

진폭이 큰 고유 변광성의 광도곡선은 수세기 동안 세페이드와 거문고자리 RR 별과 같은 극단적인 규칙성으로부터 소위 불규칙 변광성과 같은 극단적인 불규칙성까지 나타나는 행동을 보이는 것으로 알려져 왔다.모집단 II 별에서 이러한 불규칙성은 낮은 주기 W 처녀자리 변수에서 황소자리 RV 변수를 통해 반규칙형 변수들의 영역으로 점차 증가한다.항성 맥동의 저차원적 혼돈은 이 확립된 현상에 대한 현재의 해석이다.

세페이드족의 규칙적인 행동

세페이드들의 규칙적인 행동은 ^[18][19]1960년대부터 수치 유체역학으로 성공적으로 모델링되어 왔으며, 이론적인 관점에서 그것은 동력계의 ^[20]약한 산란성 때문에 생기는 중심 다양체의 존재로 쉽게 이해된다.이, 그 도구 힘없이 비선형성이다, 시스템의 진폭 equations[21][22]의 조건에 관한 자세한 설명과 맥동(제한하거나 주기), 그러한 근본적인 모드 진동, 또는 두번째 overtone 진동, 또는 더 많은 compli의 가능한 형식의 분기 도표(또한 분기 이론 보)의 건설을 허용한다.cated,여러 모드가 일정한 진폭으로 들뜨는 이중 모드 맥동.별의 진화 과정에서 맥동이 시작되는 불안정 띠의 경계는 홉 분기점에 해당합니다.

항성종족 II의 불규칙성

이와는 대조적으로, 큰 진폭의 종족 II 별들의 불규칙성은 설명하기가 더 어렵습니다.한 주기에 걸친 맥동 진폭의 변동은 큰 산란을 의미하므로 중심 매니폴드가 존재하지 않습니다.여러 가지 메커니즘이 제안되었지만 부족한 것으로 나타났습니다.첫째, 서로 부딪힐 수 있는 가까운 간격의 맥동 주파수가 여러 개 존재하지만, 적절한 항성 모형에는 그러한 주파수가 존재하지 않습니다.또 다른 더 흥미로운 제안은 변동은 확률적 ^[23]성격이지만 그렇게 큰 관측 진폭 변동에 에너지를 제공할 수 있는 메커니즘이 제안되거나 존재하지 않는다는 것이다.이제 불규칙 광선 곡선의 배후에 있는 메커니즘이 저차원 카오스 역학이라는 것이 입증되었다(카오스 이론 참조).이 결론은 두 가지 유형의 연구에 기초한다.

CFD 시뮬레이션

W Virginis 항성 모델의 시퀀스의 맥동에 대한 계산 유체 역학 수치 예측은 저차원 혼돈의 분명한 신호인 불규칙한 행동에 대한 두 가지 접근 방법을 보여줍니다.첫 번째 지표는 첫 번째 리턴 맵에서 비롯됩니다.첫 번째 리턴 맵에서는 하나의 최대 반지름 또는 다른 적절한 변수를 다음 변수에 대해 플롯합니다.모델의 시퀀스는 분기 또는 계단식 주기가 두 배로 증가하여 혼란을 초래하는 것을 보여줍니다.지도의 거의 2차 모양은 혼돈을 나타내며 말굽 지도를 ^[24][25]암시한다.모델의 다른 시퀀스는 다소 다른 경로를 따르지만 혼돈으로 가는 길, 즉 폼모-마네빌 또는 접선 분기 ^[26][27]경로를 따릅니다.

다음은 평균 표면 온도 T에 따라 다른 일련의 항성 모형에서 카오스까지의 주기가 두 배로 증가하는 유사한 시각화를 보여줍니다.그래프에는 항성 반지름(R_i, R_i+1, R_i+2) 값의 세 배가 표시되며, _{i+1 i+2} 여기서 지수는 연속된 시간 간격을 나타냅니다.

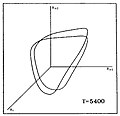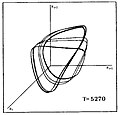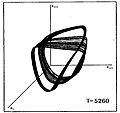P0	P2	P4	P8	밴딩 카오스	풀차오

저차원 혼돈의 존재는 또한 가장 낮은 불안정한 주기 궤도를 추출하고 위상 구조를 검사하는 모델 맥동의 더 정교한 분석에 의해 확인된다.기본 어트랙터는 Roessler 어트랙터처럼 밴드로 구성되어 있지만 ^[28]밴드 내에서 추가적인 반전이 있습니다.

관찰된 광선 곡선에서 전역 흐름 재구성

글로벌 흐름 재구성^[29] 방법은 단일 관측 신호 {s_i}을(를) 사용하여 신호를 생성한 동적 시스템의 속성을 추론합니다.첫 번째 N차원 '표준' ${\displaystyle S_{}}$ i $=$ ${\displaystyle {}_{}{i}_{}}$ , ${\displaystyle s_{}{i}_{}}$ -${\displaystyle {}_{}{1}_{}}$ , ${\displaystyle {}_{}{}_{}}$- ${\displaystyle 2_{}}$,${\displaystyle }$. s${\displaystyle {}_{}}$- N${\displaystyle {}_{}}$+ ${\displaystyle 1_{}}$({$displaystyle$S_{i}=$s_{i},s_{i-1},$s_${i-2})...$$s_{i-N+1}}$이(가) 구성됩니다.다음 단계는 시스템을 $i$에서 $시간{\displaystyle }$i + $({displaystyle$i$+$$1$로 이동시키는 비선형 $진화{\displaystyle }$ 연산자$M$({$displaystyle$ M$)$의 표현식을 찾는 것입니다. 즉, $Si$+ $1 = M(Si$은 tak의 정리에 따라 보증됩니다.내장 차원 N이 충분히 클 경우 재구성된 진화 연산자의 위상 특성은 물리적 시스템의 위상 특성과 동일하다.따라서 단일 관측 변수에 대한 지식으로부터 많은 독립 변수에 의해 지배되는 실제 물리적 시스템에 대한 특성을 추론할 수 있다.

이 접근법은 항성 R 방패자리에^[30][31] 대한 AAVSO 데이터에 적용되었다. 이 별의 불규칙한 맥동은 기초가 되는 4차원 역학에서 비롯되었다고 추론할 수 있다.다른 표현으로 표현하면, 이것은 인접한 4개의 관측치로부터 다음 관측치를 예측할 수 있다는 것을 의미합니다.물리적 관점에서 보면 시스템의 역동성을 설명하는 4가지 독립 변수가 있다고 합니다.가장 가까운 거짓 이웃의 방법은 4의 내장 치수를 입증합니다.계산된 랴푸노프 지수에서 추론한 R 스쿠티의 역학의 프랙탈 치수는 3.1과 3.2 사이에 있다.

진화 연산자의 고정점의 해석으로부터, 실니코프 ^[32]정리에 의해 기술된 시나리오인 제1의 맥동과 2:1의 공명 상태에 있는 제2의 안정된 맥동 모드에 비선형적으로 결합하는 불안정한 맥동 모드의 들뜸으로부터 맥동이 발생하는 것을 유추할 수 있다.

이 공명 메커니즘은 방패자리 R에만 국한된 것이 아니라 관측 데이터가 충분히 ^[33]양호한 다른 여러 별들을 유지하는 것으로 밝혀졌다.

「 」를 참조해 주세요.

• 맥동 백색왜성
• 맥동 무선 소스
• 별진학

레퍼런스