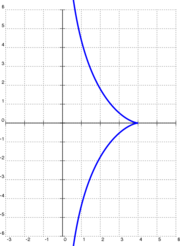
트랙트릭스

폴의 끝에 의해 생성된 트랙트릭스(지상에 평평하게 눕혀짐). 그것의 다른 끝은 한쪽으로 회전하면서 손가락에 의해 먼저 밀리고 끌려간다.

초기에

(4

.0

)

에 물체가 있는 트랙트릭스

트랙트릭스(Latin 동사 트롤리 "pull, drag"; 복수형: 트랙터)는 물체와 풀러 사이의 초기 선으로 직각으로 이동하는 트랙터(pulling) 지점에 부착된 선 세그먼트에 의해 수평면에서 마찰의 영향을 받아 물체가 움직이는 곡선이다. 그러므로 그것은 추구의 곡선이다. 1670년 클로드 페르라우트에 의해 처음 소개되었고, 이후 아이작 뉴턴(1676)과 크리스티아안 후이겐스(1693)가 연구하였다.^[1]

수학적 파생

물체가 오른쪽에 표시된 예에서 $(a,0)$ (또는 $(4,$ 0))에 있고, 원점에서 풀러가 있다고 가정하면, $a$ 는 당기는 나사산의 길이(오른쪽 예에서 4)이다. 그런 다음 풀러가 $y축$ 을 따라 양의 방향으로 움직이기 시작한다. 매 순간 실이 물체가 설명한 곡선 $y$ = $y (x)$ 에 접하여 풀러의 움직임에 의해 완전히 결정된다. 수학적으로 객체의 좌표가 ( $x,$ y $)$ 인 경우, 풀러의 y 좌표는 피타고라스 정리에 의해 $y$ + $부호(y)$ $\sqrt a 2$ – $x$ 이다². 나사산의 기울기가 곡선에 접하는 기울기와 같다고 쓰면 미분 방정식이 나온다.

{\frac {dy}{dx}=\pm {\frac {\sqrt {a^{2}-x^{2}}:{x}}}}}}

$초기$ 조건 $y (a)$ = 0. 그 해결책은

y=\int _{x}^{a}{\frac {\sqrt {a^{2}-t^{2}}}{t}}\,dt=\pm \left(a\ln {\frac {a+{\sqrt {a^{2}-x^{2}}}}{x}}-{\sqrt {a^{2}-x^{2}}}\right),

여기서 기호±는 풀러 이동 방향(양 또는 음)에 따라 달라진다.

이 해결책의 첫 번째 기간은 또한 쓰여질 수 있다.

a\backname {arsech} {\frac {x}{a},

여기서 $아치$ 는 역 쌍곡선 제분함수다.

풀러가 위쪽으로 움직이는지 아래쪽으로 움직이는지에 따라 해법 전의 기호가 달라진다. 두 가지 가지 가지 모두 트랙트릭스에 속하며, 끝 지점 $(a,0$ )에서 만난다 $.$

트랙트릭스의 기본

트랙트릭스의 필수 특성은 곡선의 $P$ 지점과 $P$ 에서 접선 선의 교차점 사이의 거리의 항상성과 곡선의 점증상이다.

트랙트릭스는 다음과 같은 여러 가지 방법으로 간주될 수 있다.

직선으로 (미끄럼 없이) 굴러가는 쌍곡선 나선형의 중심점이다.
이것은 중력장에 의해 두 지점에 부착된 완전히 유연하고 비탄력적이며 동질적인 끈을 설명하는 카트리네이션 함수의 비자발이다. 그 catenary 그 방정식 y()))cosh .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output .sf다.Rac.den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}x/a.
일정한 속도에서 일정한 방향(초기적으로 차량에 수직)으로 로프에 의해 당겨진 자동차의 뒷차축의 가운데에 의해 결정되는 궤적.
직선에서 구르는 원이 항상 수직으로 교차하는 (비선형) 곡선이다.

그 함수는 수평으로 점증하지 않는 것을 인정한다. 곡선은 Y축에 대해 대칭이다. $곡률$ 반경은 r = $요람$ $x / y$ 이다.

트랙트릭스가 가지고 있던 큰 함축은 그것의 점근에 대한 그것의 회전 표면의 연구였다: 유사권. 1868년 Eugenio Beltrami가 연구한 가우스 곡률의 일정한 표면으로서,^{[citation needed]} 유사권은 쌍곡 기하학의 국부적 모델이다. 이 아이디어는 카스너와 뉴먼이 <수학과 상상력>이라는 책에서 더 나아가서,^{[citation needed]} 그들은 트랙트릭스를 생성하기 위해 주머니 시계를 끌고 가는 장난감 기차를 보여준다.

특성.

트랙트릭스의 전멸로 Catelene.

곡선은 $x=t-\tanh(t),y=1/{\cosh(t)}$ = $x=t-\tanh(t),y=1/{\cosh(t)}$ - $x=t-\tanh(t),y=1/{\cosh(t)}$ $x=t-\tanh(t),y=1/{\cosh(t)}$ ( t $x=t-\tanh(t),y=1/{\cosh(t)}$ ) $x=t-\tanh(t),y=1/{\cosh(t)}$ , $x=t-\tanh(t),y=1/{\cosh(t)}$ = $x=t-\tanh(t),y=1/{\cosh(t)}$ / $x=t-\tanh(t),y=1/{\cosh(t)}$ $x=t-\tanh(t),y=1/{\cosh(t)}$ ( $x=t-\tanh(t),y=1/{\cosh(t)}$ ) ${\$ 등식으로 파라미터화할 수 있다 $x=t-\tanh(t),y=1/{\cosh(t)}$ ^[2]
정의된 기하학적 방법 때문에 트랙트릭스는 점근과 탄젠도 지점 사이의 탄젠트 부분의 길이가 일정하게 $a$ 인 특성을 가지고 있다.
$x$ = $x$ 와₁ $x$ = $x 2$ 사이의 한 가지 분기의 호 길이는 $ln$ $x 1 / x$ 이다₂.
트랙트릭스와 그 무증상 $pta 2 / 2$ 사이의 영역은 통합이나 마미콘의 정리를 이용하여 찾을 수 있다.
tractrix의 정규 분포(즉, tractrix의 방출)는 $y$ = $cosh$ $x / a$ 에 의해 주어지는 catwine(또는 체인 곡선)이다.
트랙트릭스를 그것의 점근에 회전시킴으로써 만들어진 혁명의 표면은 유사권이다.

실용화

1927년, P. G. A. H. Voigt는 경적을 통과하는 파도 전선이 일정한 반지름의 구형이라는 가정에 근거하여 경음기 확성기 디자인을 특허를 얻었다. 경음기 내 음의 내부반사로 인한 왜곡을 최소화하자는 취지다. 그 결과 생긴 모양은 트랙트릭스의 회전 표면이다.^[3]
판금 성형 기술에 중요한 응용이 있다. 특히 트랙트릭스 프로필은 깊은 도면을 하는 동안 판금속이 구부러지는 다이의 모서리에 사용된다.^[4]

톱니 벨트 풀리 디자인은 치아를 위한 트랙릭스 카트리네이션 모양을 사용하여 기계적 동력 전달을 위한 향상된 효율을 제공한다.^[5] 이 모양은 움직이는 톱니가 최소한의 미닫이 접촉으로 결합하고 분리되기 때문에 도르래와 결합하는 벨트 톱니의 마찰을 최소화한다. 원래 타이밍 벨트 디자인은 사다리꼴이나 원형 톱니 모양을 사용했는데, 이는 미끄럼과 마찰을 크게 일으킨다.

드로잉 머신

1692년 10~11월 크리스티아누 호이겐스는 트랙트릭스를 그리는 기계 3대를 묘사했다.^{[citation needed]}
1693년 고트프리드 빌헬름 라이프니즈는 이론적으로 어떤 1차 차등 방정식을 통합할 수 있는 "범용 견인 기계"를 고안했다.^[6] 그 개념은 트랙션 원리를 구현하는 아날로그 컴퓨팅 메커니즘이었다. 그 장치는 라이프니즈 시대의 기술로는 짓기 힘들었고, 결코 실현되지 않았다.
1706년에 존 퍼크는 쌍곡선 사분법을 실현하기 위해 견인 기계를 만들었다.^[7]
1729년에 Giovanni Poleni는 로그 기능을 그릴 수 있는 견인 장치를 만들었다.^[8]

이 모든 기계들의 역사는 H. J. M. Bos의^[9] 기사에서 볼 수 있다.

참고 항목

디니의 표면
$tanh$ , $sech$ , $csch$ , $arcosh$ 에 대한 쌍곡 함수
$ln$ 에 대한 자연 로그
$sgn용$ 부호함수
$죄$ , $cos$ , $tann$ , $arccot$ , $csc$ 에 대한 삼각 함수

메모들

^ Stillwell, John (2010). Mathematics and Its History (revised, 3rd ed.). Springer Science & Business Media. p. 345. ISBN 978-1-4419-6052-8., 345페이지 추출
^ O'Connor, John J.; Robertson, Edmund F., "Tractrix", MacTutor History of Mathematics archive, University of St Andrews
^ 경음기 라우드스피커 설계 페이지 4-5 (Wireless World, 1974년 3월)
^ Lange, Kurt (1985). Handbook of Metal Forming. McGraw Hill Book Company. p. 20.43.
^ "Gates Powergrip GT3 Drive Design Manual" (PDF). Gates Corporation. 2014. p. 177. Retrieved 17 November 2017. The GT tooth profile is based on the tractix mathematical function. Engineering handbooks describe this function as a “frictionless” system. This early development by Schiele is described as an involute form of a catenary.
^ Milici, Pietro (2014). Lolli, Gabriele (ed.). From Logic to Practice: Italian Studies in the Philosophy of Mathematics. Springer. ... mechanical devices studied ... to solve particular differential equations ... We must recollect Leibniz's 'universal tractional machine'
^ Perks, John (1706). "The construction and properties of a new quadratrix to the hyperbola". Philosophical Transactions. 25: 2253–2262. doi:10.1098/rstl.1706.0017. JSTOR 102681.
^ Poleni, John (1729). Epistolarum mathematicanim fasciculus. p. letter no. 7.
^ Bos, H. J. M. (1989). "Recognition and Wonder – Huygens, Tractional Motion and Some Thoughts on the History of Mathematics" (PDF). Euclides. 63: 65–76.

참조

Kasner, Edward; Newman, James (1940). Mathematics and the Imagination. Simon & Schuster. p. 141–143.
Lawrence, J. Dennis (1972). A Catalog of Special Plane Curves. Dover Publications. pp. 5, 199. ISBN 0-486-60288-5.

외부 링크

O'Connor, John J.; Robertson, Edmund F., "Tractrix", MacTutor History of Mathematics archive, University of St Andrews
"Tractrix". PlanetMath.
"Famous curves on the plane". PlanetMath.
수학월드의 트랙릭스
모듈: PHASER에서 Leibniz의 포켓 워치 ODE

[1] Stillwell, John (2010). Mathematics and Its History (revised, 3rd ed.). Springer Science & Business Media. p. 345. ISBN 978-1-4419-6052-8., 345페이지 추출

[2] O'Connor, John J.; Robertson, Edmund F., "Tractrix", MacTutor History of Mathematics archive, University of St Andrews

[3] 경음기 라우드스피커 설계 페이지 4-5 (Wireless World, 1974년 3월)

[4] Lange, Kurt (1985). Handbook of Metal Forming. McGraw Hill Book Company. p. 20.43.

[5] "Gates Powergrip GT3 Drive Design Manual" (PDF). Gates Corporation. 2014. p. 177. Retrieved 17 November 2017. The GT tooth profile is based on the tractix mathematical function. Engineering handbooks describe this function as a “frictionless” system. This early development by Schiele is described as an involute form of a catenary.

[6] Milici, Pietro (2014). Lolli, Gabriele (ed.). From Logic to Practice: Italian Studies in the Philosophy of Mathematics. Springer. ... mechanical devices studied ... to solve particular differential equations ... We must recollect Leibniz's 'universal tractional machine'

[7] Perks, John (1706). "The construction and properties of a new quadratrix to the hyperbola". Philosophical Transactions. 25: 2253–2262. doi:10.1098/rstl.1706.0017. JSTOR 102681.

[8] Poleni, John (1729). Epistolarum mathematicanim fasciculus. p. letter no. 7.

[9] Bos, H. J. M. (1989). "Recognition and Wonder – Huygens, Tractional Motion and Some Thoughts on the History of Mathematics" (PDF). Euclides. 63: 65–76.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Search