피타고라스 정리
Pythagorean theorem | |
| 유형 | 정리 |
|---|---|
| 들판 | 유클리드 기하학 |
| 진술 | 다리(a, b)에 있는 두 정사각형의 면적의 합은 빗변(c)에 있는 정사각형의 면적과 같습니다. |
| 기호문 | |
| 일반화 | |
| 결과들 | |
| 기하학. |
|---|
 |
| 기하학자 |
수학에서 피타고라스 정리 또는 피타고라스 정리는 유클리드 기하학에서 직각 삼각형의 세 변 사이의 기본적인 관계입니다. 빗변이 빗변(직각과 반대되는 변)인 정사각형의 넓이는 다른 두 변의 정사각형 넓이의 합과 같다는 것입니다.
이 정리는 변 a, b와 빗변 c의 길이와 관련된 방정식으로, 때때로 피타고라스 방정식이라고 불립니다.[1]
이 정리는 기원전 570년경에 태어난 그리스 철학자 피타고라스의 이름을 따서 지어졌습니다. 이 정리는 여러 가지 방법으로 여러 번 증명되었으며, 아마도 어떤 수학적 정리에서도 가장 많이 증명되었을 것입니다. 증명은 기하학적 증명과 대수학적 증명 모두를 포함하여 다양하며 일부는 수천 년 전으로 거슬러 올라갑니다.
유클리드 공간이 분석기하학에서 데카르트 좌표계로 표현될 때, 유클리드 거리는 피타고라스 관계를 만족합니다: 두 점 사이의 제곱 거리는 점 사이의 각 좌표 차이의 제곱의 합과 같습니다.
이 정리는 고차원 공간, 유클리드가 아닌 공간, 직각 삼각형이 아닌 물체, 그리고 전혀 삼각형이 아닌 n차원 입체인 물체로 다양하게 일반화될 수 있습니다. 피타고라스 정리는 문학, 연극, 뮤지컬, 노래, 우표, 만화 등에서 대중적으로 많이 언급되는 수학적 추상성, 신비성, 또는 지적 능력의 상징으로서 수학 외부의 관심을 끌어왔습니다.[citation needed]
구성된 제곱을 사용한 증명
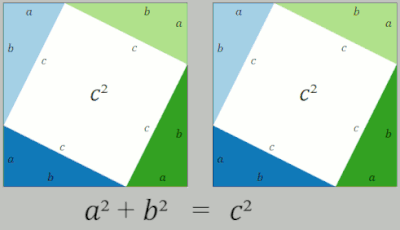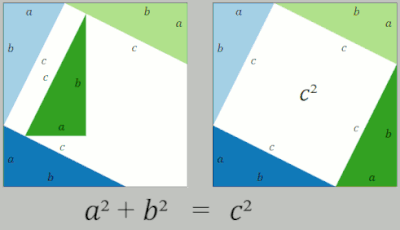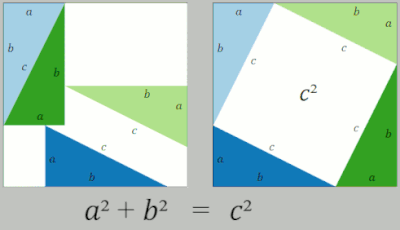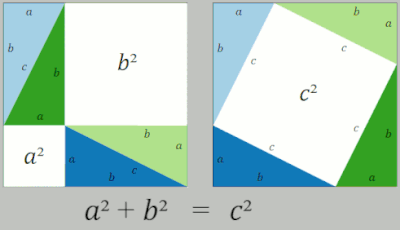
(흰색 공간의 면적은 삼각형의 번역 재배열 동안 일정하게 유지됩니다. 모든 순간에 면적은 항상 c²입니다. 그리고 마찬가지로 모든 순간에 항상 면적은 a²+b²입니다.
재배열 증명
한 재배열 증명에서, 두 개의 정사각형이 사용되는데, 그 정사각형의 변의 길이는 {\a+이고, 그 변의 길이는 a, b, c이고 빗변의 길이는 c입니다. 오른쪽 사각형은 사각형의 모서리가 삼각형에서 직각의 모서리와 대응하도록 배치되어 변의 길이가 c인 정사각형을 중앙에 형성합니다. 각 외부 사각형의 면적은(+ b) 2 + 이며, b + {\+이며 는 4개의 삼각형의 전체 면적을 나타냅니다. 왼쪽의 큰 정사각형 안에서, 네 개의 삼각형이 움직여 길이가 a와 b인 변을 가진 두 개의 비슷한 직사각형을 만듭니다. 새로운 위치에 있는 이 직사각형들은 이제 두 개의 새로운 정사각형을 묘사했습니다. 하나는 왼쪽 아래 모서리에 한 변의 길이가 a이고 다른 하나는 오른쪽 위 모서리에 한 변의 길이가 b인 정사각형입니다. 이 새로운 위치에서 이 왼쪽은 이제 의 제곱(+ b) 2 + b뿐만 아니라 + + 2 {\ + a^{+ b^{입니다 두 정사각형의 면적은(+ b) + b이므로 정사각형 면적의 다른 측도도 2 + 2 + = 2 + + a + b가 됩니다 방정식의 양변에서 4개의 삼각형의 넓이를 제거한 상태에서 것은 + = 2 입니다 {\^{ [2]
또 다른 증명에서는 두 번째 상자의 직사각형을 둘 다 정사각형의 연속된 모서리에 해당하는 하나의 모서리를 갖도록 배치할 수도 있습니다. 이러한 방식으로 두 개의 상자를 연속적으로 형성하며, 이번에는 2 및 2 를 사용하여 영역 a+ a + 2 + a를 사용하여 두 번째 정사각형을 만듭니다
영국 수학자 토마스 히스 경은 유클리드의 원소에서 명제 I.47에 대한 해설에서 이 증명을 하고, 피타고라스가 이 증명을 알고 있었을지도 모른다는 독일 수학자 칼 안톤 브레츠네이더와 헤르만 행켈의 제안을 언급합니다. 히스 자신은 피타고라스의 증명에 대한 다른 제안을 선호하지만, 그의 논의의 시작부터 "피타고라스 이후 첫 5세기 동안 우리가 소유하고 있는 그리스 문헌에는 이것 또는 그에 대한 다른 위대한 기하학적 발견을 명시하는 진술이 없다는 것"을 인정합니다.[3] 최근의 학문은 수학의 창조자로서 피타고라스가 어떤 역할을 수행할지에 대해 점점 더 많은 의문을 제기하고 있지만, 이에 대한 논쟁은 계속되고 있습니다.[4]
대수적 증명

이 정리는 도표의 아래 부분에서 보는 바와 같이 변이 c인 정사각형을 중심으로 대칭적으로 배열된 동일한 삼각형의 사본 4개를 사용하여 대수적으로 증명할 수 있습니다.[5] 이렇게 하면 정사각형이 더 커지는데, 정사각형의 변은 a + b이고 면적은 (a + b)입니다.2 네 개의 삼각형과 정사각형의 변 c는 더 큰 정사각형과 같은 면적을 가져야 합니다.
부여
유사한 증명은 변이 a, b, c인 직각 삼각형의 네 개의 복사본을 사용하며, 변이 c인 정사각형 안에 배열됩니다.[6] 삼각형은 영역 와 유사한 반면 작은 정사각형은 측면 b - a와 영역 (b - a)을 갖습니다.2 따라서 큰 정사각형의 면적은
하지만 이것은 c면과 c면이2 있는 정사각형이므로,
그 정리의 다른 증명
이 정리는 다른 어떤 것보다 더 알려진 증명을 가지고 있을 수 있습니다. (그 구별에 대한 또 다른 경쟁자인 2차 상호성의 법칙) 피타고라스 명제는 370개의 증명을 포함하고 있습니다.[7]
유사 삼각형을 사용한 증명

이 증명은 세 개의 유사 삼각형의 변의 비례성, 즉 유사 삼각형의 대응하는 어떤 두 변의 비율이 삼각형의 크기에 관계없이 동일하다는 사실에 근거합니다.
그림과 같이 직각이 C에 위치한 직각 삼각형을 ABC가 나타내도록 하자. 점 C에서 고도를 그리고 변 AB와의 교점을 Hit라고 부릅니다. 점 H는 빗변 c의 길이를 d와 d로 나눕니다. 새로운 삼각형인 ACH는 삼각형 ABC와 비슷한데, 그 이유는 둘 다 (고도의 정의에 의해) 직각을 가지고 있고, A에서의 각도를 공유하기 때문인데, 이는 그림에서 θ로 표시된 세 번째 각도가 두 삼각형 모두에서 동일할 것이라는 것을 의미합니다. 유사한 추론에 의해, 삼각형 CBH도 ABC와 유사합니다. 삼각형의 유사성을 증명하려면 다음 삼각형 공준이 필요합니다. 삼각형의 각의 합은 두 개의 직각이며 평행 공준과 같습니다. 삼각형의 유사성은 대응하는 변의 비율을 같게 합니다.
첫 번째 결과는 θ 각도의 코사인과 같고 두 번째 결과는 코사인과 같습니다.
이 비율은 다음과 같이 쓸 수 있습니다.
이 두 균등을 합하면 다음과 같은 결과를 얻을 수 있습니다.
단순화 후 피타고라스 정리를 보여줍니다.
역사에서 이 증명의 역할은 많은 추측의 대상입니다. 근본적인 의문은 유클리드가 왜 이 증명을 사용하지 않고 또 다른 증명을 발명했느냐는 것입니다. 한 가지 추측은 유사한 삼각형에 의한 증명이 비례 이론을 포함하고 있다는 것이며, 이는 원소의 후반부까지 논의되지 않은 주제이며, 그 당시에는 비례 이론이 더 발전할 필요가 있었다는 것입니다.[8]
재배열 없는 해부에 의한 아인슈타인의 증명
알버트 아인슈타인은 조각들이 움직일 필요가 없는 해부에 의한 증명을 했습니다.[9] 빗변 위의 정사각형과 다리 위의 두 개의 정사각형을 사용하는 대신 빗변을 포함하는 다른 모양과 빗변 대신 두 개의 다리 중 하나를 포함하는 두 개의 유사한 모양을 사용할 수 있습니다(세 변의 유사한 그림 참조). 아인슈타인의 증명에서 빗변을 포함하는 모양은 직각삼각형 그 자체입니다. 해부는 삼각형의 직각의 꼭짓점에서 빗변으로 수직을 떨어뜨려 삼각형 전체를 두 부분으로 나누는 것으로 구성됩니다. 그 두 부분은 원래의 직각삼각형과 같은 모양을 가지고 있으며, 원래의 삼각형의 다리를 빗변으로 가지고 있으며, 그 면적의 합은 원래의 삼각형의 그것입니다. 빗변의 제곱에 대한 직각삼각형의 넓이의 비율이 비슷한 삼각형의 경우에도 같기 때문에, 세 삼각형의 넓이 사이의 관계는 큰 삼각형의 변의 제곱에도 적용됩니다.
아인슈타인의 작도를 이용한 삼각법적 증명
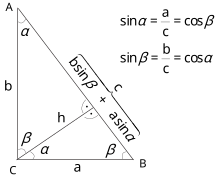
비슷한 삼각형을 사용한 증명과 아인슈타인의 증명 모두 직각 삼각형△ {\triangle}의 빗변에 대한 높이를 구성하는 것에 의존합니다 같은 구성은 사인의 정의를 직각 삼각형 안의 비율로 사용하여 피타고라스 정리의 삼각형 증명을 제공합니다.
그리하여
이 증명은 길이의 일부 비율이 사인으로 대체되는 유사 삼각형을 사용한 위의 증명과 본질적으로 동일합니다.[citation needed]
유클리드의 증명

요약하자면, 유클리드의 원소에 나오는 증명은 다음과 같이 진행됩니다. 큰 정사각형은 왼쪽과 오른쪽 직사각형으로 나누어져 있습니다. 삼각형은 왼쪽 직사각형의 절반 면적을 갖는 삼각형으로 구성됩니다. 그런 다음 가장 왼쪽에 정사각형 넓이의 절반을 갖는 또 다른 삼각형이 만들어집니다. 이 두 삼각형은 합동인 것으로 나타나 이 정사각형이 왼쪽 직사각형과 같은 면적을 가짐을 증명합니다. 이 인수 뒤에는 오른쪽 직사각형과 나머지 정사각형에 대한 유사한 버전이 뒤따릅니다. 빗변 위의 정사각형을 개혁하기 위해 두 개의 직사각형을 합하면, 그 넓이는 다른 두 정사각형의 넓이의 합과 같습니다. 자세한 내용은 다음과 같습니다.
A, B, C를 직각 A인 직각 삼각형의 꼭짓점이라 하자. 빗변 위의 사각형에서 빗변 반대쪽으로 A에서 수직인 a를 떨어 뜨립니다. 이 선은 빗변 위의 정사각형을 두 개의 직사각형으로 나누며, 각각은 다리 위의 두 정사각형 중 하나와 같은 면적을 갖습니다.
공식적인 증명을 위해서는 다음과 같은 네 가지 기본 레마타가 필요합니다.
- 만약 두 개의 삼각형이 한 변의 두 변을 다른 변의 두 변과 같게 하고, 그 변들이 포함하는 각도가 같다면, 삼각형은 합동입니다(변각 변).
- 삼각형의 면적은 같은 밑면에 있는 평행사변형의 면적의 절반이며 고도는 같습니다.
- 직사각형의 면적은 인접한 두 변의 곱과 같습니다.
- 정사각형의 넓이는 두 변의 곱과 같습니다(3에서 따옴).
다음으로, 각 위의 정사각형은 아래의 정사각형을 구성하는 두 개의 직사각형 중 하나와 차례로 관련된 다른 삼각형과 합동인 삼각형과 관련됩니다.[10]

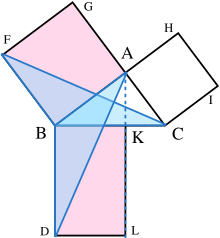
그 증명은 다음과 같습니다.
- ACB를 직각 CAB를 갖는 직각 삼각형이라고 가정합니다.
- BC, AB, CA의 각 변에는 CBDE, BAGF, ACIH 순으로 정사각형이 그려져 있습니다. 정사각형의 구성은 유클리드에서 바로 앞의 정리를 필요로 하며, 평행 공준에 의존합니다.[11]
- A부터 BD와 CE에 평행한 선을 그립니다. 각각 K와 L에서 BC와 DE를 수직으로 교차시킵니다.
- CF와 AD를 결합하여 삼각형 BCF와 BDA를 형성합니다.
- 각도 CAB와 BAG는 모두 직각이므로 C, A, G는 공선입니다.
- 각도 CBD와 FBA는 모두 직각이므로 각도 ABD는 각도 FBC와 같으며, 이는 둘 다 직각과 각도 ABC의 합이기 때문입니다.
- AB는 FB, BD는 BC, 각도 ABD는 각도 FBC와 같으므로 삼각형 ABD는 삼각형 FBC와 일치해야 합니다.
- A-K-L은 BD와 평행한 직선이기 때문에 직사각형 BDLK는 기본 BD를 공유하고 동일한 고도 BK, 즉 평행선 BD와 AL을 연결하는 공통 기본에 수직인 선을 갖기 때문에 삼각형 ABD의 두 배의 면적을 갖습니다(보조 2).
- C는 A 및 G와 공선이고, 이 선은 FB와 평행하므로, 정사각형 BAGF는 삼각형 FBC의 면적에서 두 배여야 합니다.
- 따라서 직사각형 BDLK는 정사각형 BAGF = AB와 같은 면적을 가져야 합니다.
- 그림의 다른 면에 3단계에서 10단계를 적용하면 직사각형 CKLE가 정사각형 ACIH = AC와 동일한 면적을 가져야 함을 유사하게 보여줄 수 있습니다.
- 이 두 결과를 더하면 AB + AC = BD × BK + KL × KC
- BD = KL 이므로 BD × BK + KL × KC = BD(BK + KC) = BD × BC
- 따라서 CBDE는 제곱이므로 AB + AC = BC입니다.
유클리드의 원소에서 1권의 명제 47에 나오는 이 증명은 빗변 위 정사각형의 넓이가 나머지 두 정사각형의 넓이의 합임을 보여줍니다.[12][13] 이것은 피타고라스가 사용한 증거로 추측되는 삼각형의 유사성에 의한 증명과는 상당히 구별됩니다.[14][15]
해부 및 재배열에 의한 증명
또 다른 재배열은 중간 애니메이션에 의해 제공됩니다. 큰 정사각형은 변 a, b, c가 있는 네 개의 동일한 직각 삼각형으로부터 작은 중앙 정사각형 주위에 끼워진 넓이 c로2 형성됩니다. 그런 다음 삼각형을 이동시켜 변 a와 b로 두 개의 직사각형을 만듭니다. 작은 정사각형과 이 직사각형을 결합하면 두 개의 넓이 a와2 b가2 생성되며, 이 정사각형의 넓이는 처음의 큰 정사각형과 같아야 합니다.[16]
세 번째, 가장 오른쪽 이미지도 증거를 제공합니다. 위쪽 두 정사각형은 파란색 및 녹색 음영으로 표시된 대로 분할되며, 다시 배열하면 빗변의 아래쪽 정사각형에 맞게 만들 수도 있고, 반대로 큰 정사각형은 다른 두 개를 채우는 조각으로 나눌 수도 있습니다. 한 도형을 조각으로 자르고 다른 도형을 얻기 위해 그것들을 재배열하는 이 방법을 해부라고 합니다. 이것은 큰 정사각형의 면적이 두 개의 작은 정사각형의 면적과 같다는 것을 보여줍니다.[17]
 |  |  |
면적 보존 전단에 의한 증명

첨부된 애니메이션에서 볼 수 있듯이 면적 보존 전단 매핑 및 번역은 직각에 인접한 면의 정사각형을 빗변 위의 정사각형으로 변환하여 정확하게 덮을 수 있습니다.[18] 각 전단은 바닥과 높이를 변경하지 않으므로 면적도 변경되지 않습니다. 번역은 모양을 전혀 변경하지 않기 때문에 영역을 변경하지 않습니다. 각 정사각형은 먼저 평행사변형으로 깎은 다음 빗변 위의 정사각형 한 부분으로 번역될 수 있는 직사각형으로 바뀝니다.
다른 대수적 증명
미래의 미국 대통령 제임스 A가 관련 증거를 발표했습니다. 가필드(당시 미국 대표) (도표 참조).[19][20][21] 사각형 대신 사다리꼴을 사용하는데, 사다리꼴은 안쪽 사각형의 대각선을 따라 이등분하여 위 증명의 두 번째 사각형에서 구성할 수 있으며, 그림과 같이 사다리꼴을 제공합니다. 사다리꼴의 면적은 정사각형 넓이의 절반, 즉
내부 사각형도 마찬가지로 반으로 줄이고 삼각형은 두 개만 있으므로 증명이 와 같이 진행되는데 2를 곱하여 결과를 주는 배를 제외하고는 제거됩니다.
미분을 사용한 증명
한 변의 변화가 어떻게 빗변의 변화를 일으키는지 연구하고 미적분학을 이용하면 피타고라스 정리에 도달할 수 있습니다.[22][23][24]
삼각형 ABC는 그림의 위쪽에 표시된 것처럼 직각 삼각형이며, BC는 빗변입니다. 동시에 아래 그림 부분에서 보는 바와 같이 길이 y를 빗대어 길이 x의 변 AC와 길이 a의 변 AB를 사용하여 삼각형 길이를 측정합니다.

측면 AC를 D로 약간 확장하여 x를 약간 dx 증가시키면 y도 dy 증가합니다. 이들은 (CE가 빗변에 수직이 되도록 선택된 E가 있는) 직각 삼각형인 CDE의 두 변을 형성하며, 이것은 ABC와 거의 유사한 직각 삼각형입니다. 따라서 각 변의 비율은 같아야 합니다. 즉,
이것은 으로 풀 수 방정식인 y dy = x x {\displaystyle y\,dy = x\, dx}로 다시 쓸 수 있습니다.
부여
상수는 x = 0, y = a에서 다음과 같은 식을 얻을 수 있습니다.
이것은 형식적인 증명이라기보다는 직관적인 증명에 가깝습니다. dx와 dy 대신 적절한 극한을 사용하면 더욱 엄격하게 증명할 수 있습니다.
컨버스
길이가 a, b, c인 삼각형이 주어졌을 때, a + b = c이면, 변 a와 b 사이의 각도는 직각입니다.
a + b = c가 되는 임의의 세 개의 양의 실수 a, b, c에 대하여, 삼각형 부등식의 반대 결과로 변 a, b, c가 있는 삼각형이 존재합니다.
이 역수는 유클리드의 원소(제1권, 명제 48)에 나타나 있습니다. "삼각형에서 한 변의 제곱이 나머지 두 변의 제곱의 합과 같다면, 나머지 두 변이 포함하는 각도는 옳습니다."[26]
코사인의 법칙을 사용하거나 다음과 같이 증명할 수 있습니다.
ABC를 한 변의 길이가 a, b, c이고 a + b = c인 삼각형이라고 하자. 길이가 a와 b인 변을 직각으로 포함하는 두 번째 삼각형을 구하여라. 피타고라스 정리에 따르면, 이 삼각형의 빗변은 첫 번째 삼각형의 빗변과 같은 길이 c = √a + b를 갖습니다. 두 삼각형의 변의 길이가 a, b, c이므로 삼각형은 합동이고 반드시 같은 각도를 가져야 합니다. 따라서 원래 삼각형에서 길이 a와 b의 변 사이의 각도는 직각입니다.
위의 증명은 피타고라스 정리 자체를 이용한 것입니다. 그 반대도 피타고라스 정리를 가정하지 않고도 증명할 수 있습니다.[27][28]
피타고라스 정리의 역행렬은 다음과 같이 삼각형이 옳은지 둔탁한지 급한지를 판단하는 간단한 방법입니다. 세 변 중에서 c가 가장 길고 a + b > c가 되도록 선택합니다(그렇지 않으면 삼각형 부등식에 따른 삼각형이 없습니다). 다음 문장이 적용됩니다.[29]
Edsger W. Dijkstra는 급삼각형, 우삼각형, 둔삼각형에 대한 다음 명제를 다음과 같이 표현했습니다.
- sgn(α + β − γ) = sgn(a2 + b2 − c2),
여기서 α는 a면과 반대각, β는 b면과 반대각, γ는 c면과 반대각, sgn은 부호함수입니다.
정리의 결과와 용도
피타고라스 세쌍둥이
피타고라스의 3배수는 a + b = c와 같은 3개의 양의 정수 a, b, c를 갖습니다. 즉, 피타고라스의 3배는 모든 세 변의 길이가 정수인 직각 삼각형의 변의 길이를 나타냅니다.[1] 그런 세쌍둥이는 일반적으로 (a, b, c)라고 써집니다. 잘 알려진 예로는 (3, 4, 5)와 (5, 12, 13)이 있습니다.
원시 피타고라스 3배수는 a, b, c가 코프리임(a, b, c의 최대 공약수는 1)인 것을 말합니다.
다음은 값이 100 미만인 원시 피타고라스 세쌍원소 목록입니다.
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
인버스 피타고라스 정리
a,, {\ a, c이고 가 인 직각 삼각형이 주어졌을 때(직각에서 수직으로 c c에 수직인 선). 피타고라스 정리는
역 피타고라스 정리가 다리 a a,를 d 와 연관시키는 반면[31]
방정식은 다음과 같이 변형될 수 있습니다.
where for any non-zero real . If the are to be integers, the smallest solution is then
가장 작은 피타고라스의 삼중 를 사용합니다 역 피타고라스 정리는 광학 방정식의 특별한 경우입니다.
여기서 분모는 정사각형이고 또한 변 이 정사각형인 7각 삼각형의 경우에도 마찬가지입니다.
감당할 수 없는 길이

피타고라스 정리의 결과 중 하나는 길이가 상쇄될 수 없는 선분(따라서 그 비율이 유리수가 아닌)을 직선 모서리와 나침반을 사용하여 구성할 수 있다는 것입니다. 피타고라스의 정리는 삼각형의 빗변이 제곱근 연산에 의해 변들과 관계가 있기 때문에, 헤아릴 수 없는 길이의 구성을 가능하게 합니다.
오른쪽 그림은 길이가 양의 정수의 제곱근 비율인 선분을 구성하는 방법을 보여줍니다.[32] 각 삼각형에는 측정을 위해 선택된 단위인 한 변("1"로 표시됨)이 있습니다. 피타고라스의 정리는 각 직각삼각형에서 빗변의 길이를 이 단위로 설정합니다. 만약 빗변이 완전 제곱이 아닌 양의 정수의 제곱근으로 단위와 관련되어 있다면, 그것은 √2, √3, √5와 같은 단위와 비교할 수 없는 길이의 구현입니다. 더 자세한 것은 2차 무리수를 참조하십시오.
헤아릴 수 없이 긴 길이는 피타고라스 학파의 정수론과 충돌했습니다. 피타고라스 학파는 공통 소단위의 정수배를 비교하여 비율을 다루었습니다.[33] 한 전설에 따르면, 메타폰툼의 히파수스(기원전 470년경)는 비이성적이거나 감당할 수 없는 존재를 알게 되었기 때문에 바다에서 익사했다고 합니다.[34] 히파수스의 공헌에 대한 신중한 논의는 프리츠에게서 발견됩니다.[35]
복소수

임의의 복소수에 대하여
절대값 또는 모듈러스는 다음에 의해 주어집니다.
따라서 r, x, y 세 가지 양은 피타고라스 방정식으로 연관되어 있습니다.
r은 양수 또는 0으로 정의되지만 x와 y는 양수일 수도 있고 음수일 수도 있습니다. 기하학적으로 r은 복소평면에서 원점 O 또는 영점으로부터 z의 거리입니다.
이를 일반화하여 두 점 사이의 거리, 즉1 z와2 z 사이의 거리를 구할 수 있습니다. 필요한 거리는 다음과 같습니다.
그래서 그들은 피타고라스 방정식의 버전과 관련이 있습니다.
유클리드 거리
데카르트 좌표에서의 거리 공식은 피타고라스 정리에서 유래합니다.[36] 만약 (x11, y)와 (x22, y)가 평면상의 점이라면, 유클리드 거리라고도 불리는 그들 사이의 거리는 다음과 같이 주어집니다.
보다 일반적으로, 유클리드 n-공간에서, 두 점 사이의 유클리드 거리, =( 1 2 ) {\displaystyle A\,=\, (a_{1}, a_{2},\dots, a_{n}} 및 B = (b 1, b 2, …, b) {\displaystyle B\,=\, (b_{1}, b_{2},\dots, b_{n}}는 피타고라스 정리의 일반화에 의해 다음과 같이 정의됩니다.
유클리드 거리 대신 이 값의 제곱(유클리드 거리 제곱, 또는 SED)을 사용하면 결과 방정식은 제곱근을 피하고 좌표의 SED의 합이 됩니다.
제곱 형태는 두 점의 매끄럽고 볼록한 함수로, 최소 제곱의 기초를 이루며 최적화 이론과 통계학에서 널리 사용됩니다.
다른 좌표계에서의 유클리드 거리
데카르트 좌표를 사용하지 않는 경우, 예를 들어 극좌표를 2차원으로 사용하거나 보다 일반적인 용어로 곡선좌표를 사용하는 경우, 유클리드 거리를 표현하는 공식은 피타고라스 정리보다 복잡하지만 그로부터 유도할 수 있습니다. 두 점 사이의 직선 거리가 곡선 좌표로 변환되는 전형적인 예는 물리학의 Legendre 다항식의 응용에서 찾을 수 있습니다. 그 공식들은 곡선 좌표와 데카르트 좌표를 연관시키는 방정식과 함께 피타고라스의 정리를 사용함으로써 발견될 수 있습니다. 예를 들어 극좌표(r, θ)는 다음과 같이 나타낼 수 있습니다.
그런 다음 위치(r, θ)와 (r, θ)가 있는 두 점을 거리 s로 구분합니다.
직각좌표에서의 거리에 대한 피타고라스 공식은 제곱을 수행하고 항을 결합하여 극좌표에서의 분리를 다음과 같이 산출합니다.
삼각함수 곱 대 합 공식을 사용합니다. 이 공식은 때때로 일반화된 피타고라스 정리라고 불리는 코사인의 법칙입니다.[37] 이 결과로부터 두 위치에 대한 반지름이 직각인 경우, 닫힌 각도 δ θ = π/2, 에 해당하는 되찾습니다: s = r 12 + r 22. {\displaystyle s^{2} = r_{1}^{2}+ r_{2 따라서 직각 삼각형에 유효한 피타고라스 정리는 임의의 삼각형에 유효한 보다 일반적인 코사인 법칙의 특별한 경우입니다.
피타고라스 삼각형 항등식

변 a, b, 빗변 c가 있는 직각 삼각형에서 삼각법은 변 a와 빗변 사이의 각도 θ의 사인과 코사인을 다음과 같이 결정합니다.
이를 통해 다음과 같은 결과를 얻을 수 있습니다.
마지막 단계는 피타고라스의 정리를 적용합니다. 사인과 코사인 사이의 이러한 관계는 때때로 근본적인 피타고라스 삼각형 항등식이라고 불립니다.[38] 비슷한 삼각형에서 변의 비율은 삼각형의 크기에 상관없이 같고, 각도에 따라 달라집니다. 결과적으로, 그림에서 단위 크기의 빗변이 있는 삼각형은 θ에서 크기의 반대쪽과 빗변 단위에서 크기의 cos θ의 인접한 쪽을 갖습니다.
크로스 제품 관련

피타고라스 정리는 비슷한 방법으로 교차곱과 점곱을 연결합니다.[39]
이것은 교차 곱과 점 곱의 정의에서 알 수 있습니다.
a와 b 모두에 대해 n개의 단위 벡터를 갖는 경우. 이러한 정의와 피타고라스 삼각형 항등식으로부터 관계는 다음과 같습니다.
크로스 제품을 정의하는 데도 사용할 수 있습니다. 다음 식을 재정렬하면 다음과 같이 얻을 수 있습니다.
이것은 예를 들어 7차원에서 교차 제품의 조건과 정의의 일부로 간주될 수 있습니다.[40][41]
공리로서
유클리드 기하학 공리 중 처음 네 개가 참이라고 가정하면 피타고라스 정리는 다섯 번째에 해당합니다. 즉 유클리드의 다섯 번째 공준은 피타고라스 정리와 그 반대를 의미합니다.
일반화
세 변의 유사한 수치
피타고라스 정리는 세 변의 정사각형 넓이를 넘어 비슷한 도형까지 일반화합니다. 이것은 기원전 5세기에 키오스의 히포크라테스에 의해 알려졌고,[42] 유클리드에 의해 그의 《요소》에 포함되었습니다.[43]
만약 어떤 사람이 직각 삼각형의 변에 대응하는 변을 가진 비슷한 도형(유클리드 기하학 참조)을 세운다면, 더 작은 두 변의 넓이의 합은 더 큰 변의 넓이의 합과 같습니다.
이 확장은 원래 삼각형의 변이 세 합동 도형의 대응하는 변이라고 가정합니다(따라서 유사한 도형 사이의 변의 공통 비율은 a:b:c입니다).[44] 유클리드의 증명은 볼록 다각형에만 적용되지만, 이 정리는 오목 다각형과 곡선 경계를 가진 유사한 도형에도 적용됩니다(그러나 도형의 경계 일부는 여전히 원래 삼각형의 변입니다).[44]
이 일반화의 기본 개념은 평면 도형의 넓이는 어떤 직선 차원의 제곱에 비례하고, 특히 어떤 변의 길이의 제곱에 비례한다는 것입니다. 따라서 A, B, C 영역이 있는 유사한 도형을 해당 길이 a, b, c인 측면에 세우면 다음과 같습니다.
그러나 피타고라스 정리에 의해 a + b = c 이므로 A + B = C 입니다.
반대로 피타고라스 정리를 사용하지 않고 비슷한 도형 3개에 대해 A + B = C임을 증명할 수 있다면, 우리는 그 정리의 증명을 구성하기 위해 거꾸로 작업할 수 있습니다. 예를 들어, 시작 중심 삼각형은 빗변 위의 삼각형 C로 복제되어 사용될 수 있고, 다른 두 변 위에 비슷한 직각 삼각형 두 개(A와 B)는 중심 삼각형을 고도로 나누어 구성됩니다. 따라서 두 개의 작은 삼각형의 넓이의 합은 세 번째 삼각형의 넓이의 합이므로 A + B = C이고 위 논리를 뒤집으면 피타고라스 정리 a + b = c가 됩니다. (재배치 없이 해부에 의한 아인슈타인의 증명도 참조)
 그린 영역 A + B = 블루 영역 C | 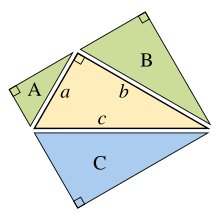 | 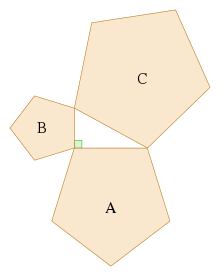 |
코사인의 법칙

피타고라스 정리는 임의의 삼각형에서 한 변의 길이와 관련된 더 일반적인 정리의 특별한 경우로, 코사인의 법칙은 다음과 같습니다.
θ \theta}가 π 2 {\displaystyle {\frac {\pi}{2}} 라디안 또는 90°일 때 cos θ = 0 {\displaystyle \cos {\theta} = 0}일 때 공식은 일반적인 피타고라스 정리로 줄어듭니다.
임의삼각형

변의 일반 삼각형의 임의의 선택된 각도에서 a, b, c는 밑면 θ의 등각이 선택된 각도와 동일하도록 이등변 삼각형을 새깁니다. 선택한 각도 θ이 c라 표시된 변의 반대라고 가정합니다. 이등변 삼각형을 새기는 것은 변 b와 변 r을 따라 c를 따라 각도 θ을 갖는 삼각형 CAD를 형성합니다. 두 번째 삼각형은 그림과 같이 a변과 c변의 길이가 서로 반대인 각 θ으로 형성됩니다. Thābit ibn Kurra는 세 삼각형의 변들은 다음과 같이 연관되어 있다고 말했습니다.[47][48]
각도 θ이 π/2에 가까워질수록 이등변삼각형의 밑면은 좁아지고, 길이 r과 s는 점점 더 적게 겹칩니다. θ = π/2일 때 ADB는 직각삼각형이 되고 r + s = c가 되어 원래의 피타고라스 정리를 되찾습니다.
한 증거는 삼각형 ABC가 삼각형 CAD와 같은 각도를 갖지만 순서가 반대라는 것을 관찰합니다. (두 삼각형은 꼭짓점 A의 각도를 공유하며, 둘 다 각도 θ을 포함하므로 삼각형 공준에 의해 동일한 세 번째 각도를 갖습니다.) 결과적으로 ABC는 하부 패널의 삼각형 DAC인 CAD의 반사와 유사합니다. θ에 대향하는 변과 인접하는 변의 비율을 취하면,
마찬가지로, 다른 삼각형의 반사를 위해서,
분수를 지우고 다음 두 관계를 추가합니다.
필요한 결과
이는 각도θ {\displaystyle \theta}가 둔각이므로 길이 r과 s가 겹치지 않는 경우에도 유효합니다.
평행사변형을 사용한 일반 삼각형
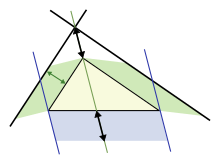
녹색영역 = 파란색영역

파푸스의 넓이 정리는 더 일반화된 것으로, 정사각형 대신에 세 변의 평행사변형을 사용하여 직각삼각형이 아닌 삼각형에 적용됩니다(물론 정사각형은 특별한 경우입니다). 위쪽 그림은 긴 면의 평행사변형이 그림과 같이 구성된 경우(화살표로 표시된 치수는 동일하고 아래쪽 평행사변형의 변을 결정하는 경우), 스케일 삼각형의 경우 가장 긴 면의 평행사변형의 면적이 다른 두 면의 평행사변형의 면적의 합임을 보여줍니다. 사각형을 평행사변형으로 대체한 것은 최초의 피타고라스의 정리와 분명히 유사하며, 서기[49][50] 4년에 알렉산드리아의 파푸스에 의해 일반화로 간주되었습니다.
아래 그림은 증명의 요소를 보여줍니다. 그림의 왼쪽에 초점을 맞춥니다. 왼쪽 녹색 평행사변형은 밑 b와 높이 h가 같기 때문에 아래 평행사변형의 왼쪽, 파란색 부분과 면적이 같습니다. 그러나 왼쪽 녹색 평행사변형도 위 그림의 왼쪽 녹색 평행사변형과 같은 면적을 갖는데, 그 이유는 밑면(삼각형의 왼쪽 위)과 삼각형의 그 변에 수직인 높이가 같기 때문입니다. 그림의 오른쪽에 대한 인수를 반복하면 아래 평행사변형은 두 개의 녹색 평행사변형의 합과 같은 면적을 갖습니다.
입체기하학


고체 기하학의 관점에서 피타고라스의 정리는 다음과 같이 3차원에 적용될 수 있습니다. 그림에 표시된 입방체를 생각해 보세요. 얼굴 대각선 AC의 길이는 피타고라스의 정리에서 다음과 같습니다.
이 세 변이 직각 삼각형을 형성하는 곳입니다. 대각선 AC와 수평 모서리 CD를 사용하여 몸체 대각선 AD의 길이는 다음과 같이 피타고라스 정리의 두 번째 적용에 의해 구합니다.
또는 한 단계에서 모든 작업을 수행합니다.
이 결과는 직교 성분 {vk}(서로 수직인 세 변)에 대한 벡터 v(대각 AD)의 크기에 대한 3차원 표현입니다.
이 한 단계 공식은 피타고라스 정리를 더 높은 차원으로 일반화한 것으로 볼 수 있습니다. 그러나 이 결과는 원래의 피타고라스 정리를 직교 평면의 연속된 직각 삼각형에 반복적으로 적용한 것에 불과합니다.
피타고라스 정리를 3차원으로 실질적으로 일반화한 것은 장 폴 드 구아 드 말베스의 이름을 딴 드 구아의 정리입니다. 정사면체에 직각의 모서리가 있는 경우(입방체의 모서리와 같은), 직각의 모서리와 반대쪽 면의 넓이의 제곱은 다른 세 면의 넓이의 제곱의 합입니다. 이 결과는 "n차원 피타고라스 정리"와 같이 일반화될 수 있습니다.[51]
를 R의n 직교 벡터라고 합니다. 정점이 1 0인 n차원 단순 S를 생각해 보자 ( 정점이 1 원점을 S의 "하이포텐 사용"으로, 나머지 (n - 1)차원 면을 "다리"로 포함하지 않음.) 그렇다면 S의 빗변 부피의 제곱은 n개의 다리 부피의 제곱의 합입니다.
이 문장은 그림의 사면체에 의해 3차원으로 설명됩니다. "하이포텐유즈"는 도형의 뒤쪽에 있는 사면체의 밑면이고, "다리"는 전경의 꼭짓점에서 나오는 세 개의 면입니다. 꼭짓점에서 밑부분의 깊이가 증가함에 따라 "다리"의 면적은 증가하는 반면 밑부분의 면적은 고정됩니다. 이 정리는 이 깊이가 오른쪽 꼭짓점을 생성하는 값에 있을 때 피타고라스 정리의 일반화가 적용됨을 시사합니다. 다른 표현으로:[52]
n-직각 n차원 심플렉스가 주어지면 오른쪽 꼭짓점에 반대하는 면의 (n - 1)-내용의 제곱은 나머지 면의 (n - 1)-내용의 제곱의 합과 같습니다.
내부제품공간

피타고라스 정리는 익숙한 2차원과 3차원 유클리드 공간의 일반화인 [53]내적 공간으로 일반화될 수 있습니다. 예를 들어, 함수 분석에서와 같이 함수는 내부 곱 공간에서 성분이 무한히 많은 벡터로 간주될 수 있습니다.[54]
내부 곱 공간에서 수직성의 개념은 직교성의 개념으로 대체됩니다: 두 벡터 와는 내부 곱⟩w⟨ {\{v},\mathbf {w} \rangle }가 0이면 직교합니다. 내적은 벡터의 내적을 일반화한 것입니다. 점 제품은 표준 내부 제품 또는 유클리드 내부 제품이라고 합니다. 하지만 다른 내부 제품은 가능합니다.[55]
길이의 개념은 다음과 같이 정의되는 벡터 v의 표준 ‖v ‖의 개념으로 대체됩니다.
내적 공간에서 피타고라스 정리는 임의의 두 직교벡터 v와 w에 대하여
여기서 벡터 v와 w는 벡터 합 v + w에 의해 주어진 빗변을 갖는 직각 삼각형의 변과 유사합니다. 피타고라스 정리의 이러한 형태는 내적인 성질의 결과입니다.
서 ⟨ v, ⟩ =⟨ w, v ⟩ = 0 \mathbf {v,\ w} \rangle =\langle \mathbf {w,\ v} \rangle = 0}은 직교성 때문입니다.
내부 곱 공간에서 비직교 벡터에 대한 피타고라스 정리의 추가적인 일반화는 평행사변형 법칙입니다.[56]
평행사변형의 변의 길이 제곱의 두 배는 대각선의 길이 제곱의 합이라는 뜻입니다. 이 동등성을 만족하는 모든 규범은 내적에 해당하는 사실상의 규범입니다.[56]
피타고라스 항등식은 2개 이상의 직교 벡터의 합으로 확장될 수 있습니다. 만약1 v, v2, ..., v가n 내적 공간에서 쌍대 직교 벡터라면, 피타고라스 정리를 이 벡터들의 연속적인 쌍(고체기하학의 절에서 3차원에 대해 설명한 바와 같이)에 적용하면 방정식은[57] 다음과 같이 됩니다.
n차원 공간의 m차원 객체 집합
피타고라스 정리의 또 다른 일반화는 어떤 차원이든 레베그 측정 가능한 물체 집합에 적용됩니다. 구체적으로, n차원 유클리드 공간의 하나 이상의 평행 m차원 평면에 있는 물체의 m차원 집합의 측정 제곱은 모든 m차원 좌표 부분 공간에 대한 물체의 직교 투영 측정의 제곱의 합과 같습니다.[58]
수학 용어로:
위치:
- 는 m차원(1차원의 길이, 2차원의 면적, 3차원의 부피 등) 단위입니다.
- 는 n차원 유클리드 공간의 하나 이상의 평행 m차원 평면에 있는 하나 이상의 중첩되지 않는 m차원 객체의 집합입니다.
- 는 m차원 객체 집합의 총 측도(합)입니다.
- 는 직교 좌표 부분 공간에 대한 원본 집합의 m차원 투영을 나타냅니다.
- 는 m차원 좌표 i i에 대한 m차원 집합 투영의 측도입니다 객체 투영은 좌표 부분공간에서 겹칠 수 있으므로 집합 내 각 객체 투영의 측도는 개별적으로 계산되어야 합니다. 그런 다음 주어진 좌표 부분공간의 사영 집합에 대한 총 측도를 제공하기 위해 추가된 모든 사영의 측도.
- 는 m차원 객체가 투영되는 n차원 공간(Rn)의 직교, m차원 좌표 부분공간의 수이다(m≤ n):
비유클리드 기하학
피타고라스 정리는 유클리드 기하학의 공리에서 파생된 것으로, 사실 피타고라스 정리가 어떤 직각 삼각형에 대해 실패했다면, 이 삼각형이 포함된 평면은 유클리드가 될 수 없습니다. 더 정확히 말하면, 피타고라스 정리는 유클리드의 평행(제5) 공준을 암시하고 암시합니다.[59][60] 따라서 비유클리드 기하학에서[61] 직각삼각형은 피타고라스 정리를 만족하지 않습니다. 예를 들어, 구면기하학에서 단위구의 팔분의 일을 경계로 하는 직각삼각형(a, b, c)의 모든 변의 길이는 π/2이고, 모든 각도는 직각이므로 + b = 2 2 > c 2 {\displaystyle a^{2}+b^{2이기 에 피타고라스 정리에 위배됩니다.2c}>c^{2
여기서 비유클리드 기하학의 두 가지 경우, 즉 구면 기하학과 쌍곡면 기하학이 고려됩니다. 각각의 경우, 비유클리드 삼각형의 경우와 마찬가지로 피타고라스 정리를 대체하는 결과는 적절한 코사인 법칙에서 따릅니다.
그러나 삼각형이 옳다는 조건을 A+B = C와 같이 두 개의 각도가 3분의 1에 합하는 조건으로 바꾸면 쌍곡기하학과 타원기하학에서 피타고라스 정리는 여전히 유효합니다. 그러면 두 변은 다음과 같이 연관됩니다. 지름이 a와 b인 원의 넓이의 합은 지름이 c인 원의 넓이와 같습니다.[62]
구면기하학

반지름 R인 구면 위의 임의의 직각 삼각형(예를 들어, 그림의 γ이 직각인 경우)에 대하여, 변들이 a, b, c인 경우, 변들 사이의 관계는 다음과 같은 형태를 취합니다.
이 식은 모든 구면 삼각형에 적용되는 코사인 구면 법칙의 특별한 경우로 유도될 수 있습니다.
구면 위의 무한소 삼각형(또는 이와 동등하게 무한반지름의 구면 위의 유한 구면 삼각형의 경우)의 경우, 직각 삼각형의 변 사이의 구면 관계는 피타고라스 정리의 유클리드 형태로 축소됩니다. 방법을 알기 위해서, 우리는 반지름이 R인 구 위에 고정된 변의 길이가 a, b, c인 구면 삼각형을 갖는다고 가정합니다. R이 무한대에 접근함에 따라 a/R, b/R 및 c/R 양은 0으로 감소하고 구 피타고라스 은 1 = 1=1로 감소하므로 점근적 확장을 살펴봐야 합니다.
코사인 함수에 대한 Maclaurin 급수는 = 1 -x 2 + O (x 4) {\textstyle \cos x = 1-{\tfrac {1}{2}}x^{2}+O{\left(x^{4}\right)}}로 표기할 수 있으며 나머지 항은 큰 O 표기법으로 표시됩니다. = /R {\displaystyle x = c/R}을 삼각형의 한 변이라 하고, 고정된 c에 대하여 R로 표현하면,
a와 b에 대해서도 마찬가지입니다. 각 코사인에 대한 점근 전개를 직각 삼각형에 대한 구면 관계로 대입하면 다음과 같은 결과가 나옵니다.
1을 뺀 다음 각 면을 부정하는 것,
2R을2 곱하면 고정된 a, b 및 변수 R에 대한 c의 점근적 전개는
유클리드 피타고라스 관계 2 = a + 2 {\textstyle c} = a} + b^{2반지름 R이 무한대에 가까워지면 나머지가 사라지기 때문에 극한에서 복구됩니다.
작은 직각 삼각형이 있는 구면 삼각법에서 실질적인 계산을 위해, 코사인은 유의성 손실을 피하기 위해 이중 각도 동일성 2 θ = 1 - 2 sin 2 θ {\displaystyle \cos {2\theta} = 1-2\sin ^{\theta }}를 사용하여 사인으로 대체할 수 있습니다. 그러면 구면의 피타고라스 정리는 교대로 다음과 같이 쓸 수 있습니다.
쌍곡기하학

가우스 곡률이 -1/R로2 균일한 쌍곡 공간에서 다리가 a, b, 빗변이 c인 직각 삼각형의 경우, 변 사이의 관계는 다음과 같은 형태를 취합니다.[64]
여기서 cosh는 쌍곡 코사인입니다. 이 공식은 모든 쌍곡 삼각형에 적용되는 코사인의 쌍곡 법칙의 특별한 형태입니다.[65]
γ를 사용하면 변 c의 반대쪽 꼭짓점의 각도입니다.
쌍곡 코사인인 cosh x ≈ 1 + x/2에 대해 Maclaurin 급수를 사용함으로써 쌍곡 삼각형이 매우 작아짐에 따라(즉, a, b, call이 0에 가까워짐에 따라) 직각 삼각형에 대한 쌍곡 관계가 피타고라스 정리의 형태에 접근함을 알 수 있습니다.
작은 직각 삼각형(a, b << R)에 대하여, 쌍곡 코사인을 제거하여 유의성의 손실을 피할 수 있으며,
아주 작은 삼각형
빗변이 c인 매우 작은 직각삼각형(Ka2, Kb2 << 1)에서 임의의 균일한 곡률 K(양, 영, 음)에 대하여, 다음과 같이 나타낼 수 있습니다.
미분기하학

피타고라스 정리는 미분기하학에서 볼 수 있는 무한소 삼각형에 적용됩니다. 3차원 공간에서 무한히 분리된 두 점 사이의 거리는 다음을 만족합니다.
ds를 사용하여 거리의 요소와 (dx, dy, dz) 두 점을 분리하는 벡터의 구성 요소를 사용합니다. 그런 공간을 유클리드 공간이라고 합니다. 그러나 리만 기하학에서 일반 좌표(데카르트뿐만 아니라)와 일반 공간(유클리드뿐만 아니라)에 유용한 이 표현의 일반화는 다음과 같은 형태를 취합니다.[66]
이를 미터 텐서라고 합니다. (가끔 언어의 남용으로 계수 g의ij 집합에 동일한 항이 적용됩니다.) 위치의 함수일 수 있으며 종종 곡선 공간을 설명합니다. 간단한 예는 곡선 좌표로 표현된 유클리드(평탄한) 공간입니다. 예를 들어 극좌표의 경우:
역사

피타고라스 정리가 한 번 발견된 것인지, 여러 곳에서 여러 번 발견된 것인지에 대해서는 논쟁이 있고, 최초의 증명 날짜와 마찬가지로 최초의 발견 날짜는 불확실합니다. 메소포타미아 수학의 역사학자들은 피타고라스가 태어나기 전인 천 년이 넘는 고대 바빌로니아 시대(기원전 20세기~16세기) 동안 피타고라스의 법칙이 널리 사용되었다고 결론지었습니다.[68][69][70][71] 정리의 역사는 피타고라스의 세쌍원소에 대한 지식, 직각삼각형의 변들 사이의 관계에 대한 지식, 인접한 각들 사이의 관계에 대한 지식, 그리고 어떤 연역 체계 내에서의 정리의 증명 등 네 부분으로 나눌 수 있습니다.
기원전 1800년에 쓰여진 이집트의 중세 왕국 베를린 파피루스 6619에는 피타고라스의 세쌍원소 6:8:10이 풀이인 문제가 포함되어 있지만 문제에는 삼각형이 언급되어 있지 않습니다. 라르사 근처에서 기원전 1800년에 쓰여진 메소포타미아의 정제 플림톤 322는 피타고라스의 세쌍원소와 밀접한 관련이 있는 많은 항목을 포함하고 있습니다.[72]
인도에서, 기원전 8세기에서 5세기 사이에 다양한 날짜가 제시된 [73]보더하야나 슐바 경전은 피타고라스의 세쌍원소 목록과 피타고라스 정리의 진술을 포함하고 있는데, 이는 이등변형 직각삼각형의 특별한 경우와 일반적인 경우 모두에 해당합니다(c.기원전 600년).[a]
비잔티움 신플라톤 철학자이자 수학자인 프로클로스는 서기 5세기에 저술한 두 가지 산술 규칙을 언급하고 있는데, "그 중 하나는 플라톤에게, 다른 하나는 피타고라스에게 귀속된다"[75]고 언급하고 있습니다. 피타고라스의 법칙(기원전 570년 – 기원전 495년)c.은 홀수에서 시작하여 다리와 빗변이 한 단위씩 다른 삼중항을 생성하고, 플라톤의 법칙(기원전 428년/427년 또는 424년/423년 – 348년/347년)은 짝수에서 시작하여 다리와 빗변이 두 단위씩 다른 삼중항을 생성합니다. 토마스 L에 의하면. 히스(Hath, 1861–1940), 피타고라스가 살고 난 후 5세기 동안 남아있는 그리스 문헌에는 피타고라스에 대한 이 정리의 특별한 귀속이 없습니다.[76] 그러나 플루타르코스와 키케로와 같은 작가들이 그 정리를 피타고라스의 것으로 돌렸을 때, 그들은 그 귀속이 널리 알려져 있고 의심할 여지가 없다는 것을 암시하는 방식으로 그렇게 했습니다.[77][78] 고전주의자 쿠르트 폰 프리츠(Kurt von Fritz)는 "이 공식이 개인적으로 피타고라스의 것으로 옳은지... 피타고라스 수학의 가장 오래된 시대에 속하는 것으로 안전하게 추정할 수 있습니다."[35] 기원전 300년경, 유클리드의 《유클리드의 원소》에서, 이 정리에 대한 현존하는 가장 오래된 공리적 증명이 제시됩니다.[79]

훨씬 이전에 알려진 내용이지만, 대략 기원전 1세기부터 남아있는 문헌에서, 중국의 본문인 저우비 수안징(周髀算经)은 (3, 4, 5)삼각형에 대한 피타고라스 정리에 대한 추론을 제공합니다. 중국에서는 그것을 "구구 정리"(勾股定理)라고 부릅니다. 한나라 (기원전 202년~기원후 220년) 동안, 피타고라스의 세쌍둥이는 직각삼각형에 [82]대한 언급과 함께 "수학기술 9장"에 등장합니다.[83] 어떤 이들은 이 정리가 중국에서 처음 생겨났다고 믿고 있는데, 이 정리는 주공의 천문학자이자 수학자의 이름을 따서 "상가오 정리" (商高定理)라고도 알려져 있는데, 그의 추론은 주비수안징에 있는 것의 대부분을 차지했습니다.
참고 항목
참고사항 및 참고사항
메모들
참고문헌
- ^ a b Judith D. Sally; Paul Sally (2007). "Chapter 3: Pythagorean triples". Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore. p. 63. ISBN 978-0-8218-4403-8.
- ^ 벤슨, 도날드. 증명의 순간 : 수학적 깨달음, pp. 172–173 (Oxford University Press, 1999).
- ^ Euclid (1956), pp. 351–352
- ^ Huffman, Carl (23 February 2005). "Pythagoras". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Winter 2018 Edition).Huffman, Carl (23 February 2005). "Pythagoras". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Winter 2018 Edition)."피타고라스가 수학자이자 과학자였는지에 대한 질문을 다루는데 있어서 출처에 대한 결정이 중요하다는 것은 이제 분명해야 합니다. 피타고라스가 수학자도 아니고 과학자도 아니었던 이 부분의 첫 다섯 단락에 그려진 우주에 대한 견해는 여전히 일치하고 있습니다."
- ^ Alexander Bogomolny. "Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #4". Cut the Knot. Retrieved 4 November 2010.
- ^ Alexander Bogomolny. "Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3". Cut the Knot. Retrieved 4 November 2010.
- ^ (loomis 1940)
- ^ (2007년 10월 39일자)
- ^ Schroeder, Manfred Robert (2012). Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. Courier Corporation. pp. 3–4. ISBN 978-0486134789.
- ^ 예를 들어 전단 매핑에 의한 피타고라스 정리 참조 Wayback Machine, Saint Louis University 웹사이트 Java 애플릿에서 아카이브된 2016-10-14
- ^ Jan Gullberg (1997). Mathematics: from the birth of numbers. W. W. Norton & Company. p. 435. ISBN 0-393-04002-X.
- ^ Heiberg, J.L. "Euclid's Elements of Geometry" (PDF). pp. 46–47.
- ^ "Euclid's Elements, Book I, Proposition 47". 교수님의 Java 애플릿을 사용한 웹 페이지 버전도 참조하십시오. 데이비드 E. 조이스, 클라크 대학.
- ^ Stephen W. Hawking (2005). God created the integers: the mathematical breakthroughs that changed history. Philadelphia: Running Press Book Publishers. p. 12. ISBN 0-7624-1922-9. 이 증명은 유클리드 증명을 확인하기 위해 컴퓨터 프로그램이 설정된 후 처음 등장했습니다.
- ^ 비율 이론은 피타고라스 이후 불과 2세기 만에 개발되었기 때문에 피타고라스의 증명은 일반적인 것이 아닐 수도 있습니다. (Maor 2007, 25쪽) 참조.
- ^ Alexander Bogomolny. "Pythagorean theorem, proof number 10". Cut the Knot. Retrieved 27 February 2010.
- ^ (Loomis 1940, p. 113, 기하학적 증명 22 및 그림 123)
- ^ Polster, Burkard (2004). Q.E.D.: Beauty in Mathematical Proof. Walker Publishing Company. p. 49.
- ^ 주간 수학 칼럼에 게재됨: 수학 날짜 달력과 에서 언급된 바와 같이: 1876년 4월 1일 Wayback Machine by V에서 2010년 7월 14일 보관. 프레데릭 리치
- ^ Lantz, David. "Garfield's proof of the Pythagorean Theorem". Math.Colgate.edu. Archived from the original on 2013-08-28. Retrieved 2018-01-14.
- ^ Maor, Eli, The Pythagorean Theorem, Princeton University Press, 2007: pp. 106-107.
- ^ Mike Staring (1996). "The Pythagorean proposition: A proof by means of calculus". Mathematics Magazine. Mathematical Association of America. 69 (1): 45–46. doi:10.2307/2691395. JSTOR 2691395.
- ^ Bogomolny, Alexander. "Pythagorean Theorem". Interactive Mathematics Miscellany and Puzzles. Alexander Bogomolny. Archived from the original on 2010-07-06. Retrieved 2010-05-09.
- ^ Bruce C. Berndt (1988). "Ramanujan – 100 years old (fashioned) or 100 years new (fangled)?". The Mathematical Intelligencer. 10 (3): 24–31. doi:10.1007/BF03026638. S2CID 123311054.
- ^ Judith D. Sally; Paul J. Sally Jr. (2007-12-21). "Theorem 2.4 (Converse of the Pythagorean theorem).". Roots to Research. American Mathematical Society. pp. 54–55. ISBN 978-0-8218-4403-8.
- ^ 유클리드의 원소들, 제1권, D.E.로부터의 명제 48. 클라크 대학의 조이스 웹페이지
- ^ Casey, Stephen, "피타고라스 정리의 역방향", Mathematical Gazet 92, 2008년 7월 309–313.
- ^ Mitchell, Douglas W., "92.47에 대한 피드백", Mathematical Gazet 93, 2009년 3월 156.
- ^ Ernest Julius Wilczynski; Herbert Ellsworth Slaught (1914). "Theorem 1 and Theorem 2". Plane trigonometry and applications. Allyn and Bacon. p. 85.
- ^ Dijkstra, Edsger W. (September 7, 1986). "On the theorem of Pythagoras". EWD975. E. W. Dijkstra Archive.
- ^ Alexander Bogomolny, 피타고라스의 역수 정리, https://www.cut-the-knot.org/pythagoras/PTForReciprocals.shtml
- ^ Law, Henry (1853). "Corollary 5 of Proposition XLVII (Pythagoras's Theorem)". The Elements of Euclid: with many additional propositions, and explanatory notes, to which is prefixed an introductory essay on logic. John Weale. p. 49.
- ^ Shaughan Lavine (1994). Understanding the infinite. Harvard University Press. p. 13. ISBN 0-674-92096-1.
- ^ 히파수스는 그 당시 항해 중이었고, 그의 동료들은 히파수스를 배 밖으로 내던졌습니다. 참조
- ^ a b Kurt Von Fritz (Apr 1945). "The Discovery of Incommensurability by Hippasus of Metapontum". Annals of Mathematics. Second Series. 46 (2): 242–264. doi:10.2307/1969021. JSTOR 1969021.
- ^ Jon Orwant; Jarkko Hietaniemi; John Macdonald (1999). "Euclidean distance". Mastering algorithms with Perl. O'Reilly Media, Inc. p. 426. ISBN 1-56592-398-7.
- ^ Wentworth, George (2009). Plane Trigonometry and Tables. BiblioBazaar, LLC. p. 116. ISBN 978-1-103-07998-8.Wentworth, George (2009). Plane Trigonometry and Tables. BiblioBazaar, LLC. p. 116. ISBN 978-1-103-07998-8.연습문제 116페이지
- ^ Lawrence S. Leff (2005). PreCalculus the Easy Way (7th ed.). Barron's Educational Series. p. 296. ISBN 0-7641-2892-2.
- ^ WS Massey (Dec 1983). "Cross products of vectors in higher-dimensional Euclidean spaces" (PDF). The American Mathematical Monthly. Mathematical Association of America. 90 (10): 697–701. doi:10.2307/2323537. JSTOR 2323537. S2CID 43318100. Archived from the original (PDF) on 2021-02-26.
- ^ Pertti Lounesto (2001). "§7.4 Cross product of two vectors". Clifford algebras and spinors (2nd ed.). Cambridge University Press. p. 96. ISBN 0-521-00551-5.
- ^ Francis Begnaud Hildebrand (1992). Methods of applied mathematics (Reprint of Prentice-Hall 1965 2nd ed.). Courier Dover Publications. p. 24. ISBN 0-486-67002-3.
- ^ 히스, T. L., 그리스 수학의 역사, 옥스포드 대학 출판부, 1921; 도버에 의해 재인쇄, 1981.
- ^ 유클리드의 요소: 책 VI, 명제 VI 31 "직각삼각형에서 직각을 나타내는 변의 도형은 직각을 포함하는 변의 도형과 유사하고 유사하게 묘사된 도형과 같습니다."
- ^ a b Putz, John F. and Sipka, Timothy A. "피타고라스 정리의 일반화에 관하여", The College Mathematics Journal 34 (4), 2003년 9월, 291-295쪽.
- ^ Lawrence S. Leff (2005-05-01). cited work. Barron's Educational Series. p. 326. ISBN 0-7641-2892-2.
- ^ Howard Whitley Eves (1983). "§4.8:...generalization of Pythagorean theorem". Great moments in mathematics (before 1650). Mathematical Association of America. p. 41. ISBN 0-88385-310-8.
- ^ Aydin Sayili (Mar 1960). "Thâbit ibn Qurra's Generalization of the Pythagorean Theorem". Isis. 51 (1): 35–37. doi:10.1086/348837. JSTOR 227603. S2CID 119868978.
- ^ Judith D. Sally; Paul Sally (2007-12-21). "Exercise 2.10 (ii)". Roots to Research: A Vertical Development of Mathematical Problems. American Mathematical Soc. p. 62. ISBN 978-0-8218-4403-8.
- ^ 이러한 공사에 대한 자세한 내용은
- ^ 클라우디 알시나, 로저 B. 넬센: 매력적인 증명: 우아한 수학으로의 여행. MAA, 2010, ISBN 9780883853481, 페이지 77–78 (단, 페이지 77, Google Books)
- ^ Rajendra Bhatia (1997). Matrix analysis. Springer. p. 21. ISBN 0-387-94846-5.
- ^ 이 일반화에 대한 확장된 논의는 예를 들어 Willie W를 참조하십시오. Wong Archive the Wayback Machine 2002, 일반화된 n차원 피타고라스 정리에서 2009-12-29.
- ^ Ferdinand van der Heijden; Dick de Ridder (2004). Classification, parameter estimation, and state estimation. Wiley. p. 357. ISBN 0-470-09013-8.
- ^ Qun Lin; Jiafu Lin (2006). Finite element methods: accuracy and improvement. Elsevier. p. 23. ISBN 7-03-016656-6.
- ^ Howard Anton; Chris Rorres (2010). Elementary Linear Algebra: Applications Version (10th ed.). Wiley. p. 336. ISBN 978-0-470-43205-1.
- ^ a b c Karen Saxe (2002). "Theorem 1.2". Beginning functional analysis. Springer. p. 7. ISBN 0-387-95224-1.
- ^ Douglas, Ronald G. (1998). Banach Algebra Techniques in Operator Theory (2nd ed.). New York, New York: Springer-Verlag New York, Inc. pp. 60–61. ISBN 978-0-387-98377-6.
- ^ Donald R Conant & William A Beyer (Mar 1974). "Generalized Pythagorean Theorem". The American Mathematical Monthly. Mathematical Association of America. 81 (3): 262–265. doi:10.2307/2319528. JSTOR 2319528.
- ^ Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd ed.). CRC Press. p. 2147. ISBN 1-58488-347-2.
The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.
- ^ Alexander R. Pruss (2006). The principle of sufficient reason: a reassessment. Cambridge University Press. p. 11. ISBN 0-521-85959-X.
We could include...the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate.
- ^ Stephen W. Hawking (2005). cited work. Running Press. p. 4. ISBN 0-7624-1922-9.
- ^ Victor Pambuccian (December 2010). "Maria Teresa Calapso's Hyperbolic Pythagorean Theorem". The Mathematical Intelligencer. 32 (4): 2. doi:10.1007/s00283-010-9169-0.
- ^ Barrett O'Neill (2006). "Exercise 4". Elementary Differential Geometry (2nd ed.). Academic Press. p. 441. ISBN 0-12-088735-5.
- ^ Saul Stahl (1993). "Theorem 8.3". The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. p. 122. ISBN 0-86720-298-X.
- ^ Jane Gilman (1995). "Hyperbolic triangles". Two-generator discrete subgroups of PSL(2,R). American Mathematical Society Bookstore. ISBN 0-8218-0361-1.
- ^ Tai L. Chow (2000). Mathematical methods for physicists: a concise introduction. Cambridge University Press. p. 52. ISBN 0-521-65544-7.
- ^ Neugebauer 1969, 36쪽.
- ^ 노이바우어 1969: p. 36 "다시 말해서, 직각 삼각형의 변의 길이에 있는 제곱의 합은 빗변의 길이의 제곱과 같다는 것이 바빌로니아 수학의 전체 기간 동안 알려졌습니다."
- ^ Friberg, Jöran (1981). "Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations". Historia Mathematica. 8: 277–318. doi:10.1016/0315-0860(81)90069-0.Friberg, Jöran (1981). "Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations". Historia Mathematica. 8: 277–318. doi:10.1016/0315-0860(81)90069-0.p. 306 "플림프턴 322는 그 종류의 독특한 텍스트이지만, 피타고라스 정리가 고대 바빌로니아 시대의 수학자들에게 잘 알려져 있었다는 것을 증명하는 몇 가지 다른 알려진 텍스트가 있습니다."
- ^ Høyrup, Jens. "Pythagorean 'Rule' and 'Theorem' – Mirror of the Relation Between Babylonian and Greek Mathematics". In Renger, Johannes (ed.). Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin (PDF). Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. pp. 393–407.Høyrup, Jens. "Pythagorean 'Rule' and 'Theorem' – Mirror of the Relation Between Babylonian and Greek Mathematics". In Renger, Johannes (ed.). Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin (PDF). Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. pp. 393–407.p. 406, "따라서 이 증거만으로 판단하자면, 피타고라스의 규칙은 기원전 2300년에서 1825년 사이에 Db-146에서2 처리된 문제에서 파생된 것으로 일반 측량사의 환경에서 발견되었을 가능성이 있습니다." (Db-146은2 직사각형의 넓이와 대각선이 주어진 면의 계산에 관한 에슈눈나의 고대 바빌로니아 점토판입니다.)
- ^ Robson, E. (2008). Mathematics in Ancient Iraq: A Social History. Princeton University Press.Robson, E. (2008). Mathematics in Ancient Iraq: A Social History. Princeton University Press.109쪽 "많은 고대 바빌로니아 수학자들… 직각삼각형의 대각선에 있는 사각형은 길이와 너비의 사각형의 합과 같은 면적을 가지고 있다는 것을 알고 있었습니다: 그 관계는 에슈누나, 시파, 수사, 에슈누나, 시파르, 그리고 일곱 개의 다른 판에 '대수'를 자르고 붙이는 단어 문제에 대한 작업된 해결책에서 사용되었습니다. 그리고 바빌로니아 남부의 알려지지 않은 장소."
- ^ Robson, Eleanor (2001). "Neither Sherlock Holmes nor Babylon: a reassessment of Plimpton 322". Historia Mathematica. 28 (3): 167–206. doi:10.1006/hmat.2001.2317.
- ^ Kim Plofker (2009). Mathematics in India. Princeton University Press. pp. 17–18. ISBN 978-0-691-12067-6.
- ^ Carl Benjamin Boyer; Uta C. Merzbach (2011). "China and India". A history of mathematics (3rd ed.). Wiley. p. 229. ISBN 978-0470525487.
Quote: [In Sulba-sutras,] we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid's Elements. (...)
- ^ Proclus (1970). A Commentary of the First Book of Euclid's Elements. Translated by Morrow, Glenn R. Princeton University Press. 428.6.
- ^ "Introduction and books 1,2". The University Press. March 25, 1908 – via Google Books.
- ^ (히스 1921년, 제1권, 페이지 144): "비록 이것이 전통에 의해 피타고라스라는 이름과 보편적으로 연관된 명제이지만, 피타고라스가 실제로 발견했다는 정말 믿을 만한 증거는 없습니다. 상대적으로 늦은 작가들은 그의 발견을 축하하기 위해 소를 제물로 바쳤다는 이야기를 덧붙입니다."
- ^ 역사적 증거에 대한 광범위한 논의가 (Euclid 1956, 페이지 351) 페이지=351에 제공됩니다.
- ^ Asger Aaboe (1997). Episodes from the early history of mathematics. Mathematical Association of America. p. 51. ISBN 0-88385-613-1.
...it is not until Euclid that we find a logical sequence of general theorems with proper proofs.
- ^ Robert P. Crease (2008). The great equations: breakthroughs in science from Pythagoras to Heisenberg. W W Norton & Co. p. 25. ISBN 978-0-393-06204-5.
- ^ 주비의 여러 문헌의 기원에 대한 다소 광범위한 논의는 다음과 같습니다.
- ^ 이 작품은 246개의 문제를 엮은 것으로, 그 중 일부는 기원전 213년의 책 불태우기에서 살아남아 서기 100년 이전에 최종적인 형태로 완성되었습니다. 서기 263년에 류휘가 광범위하게 언급했습니다. 특히 §3: 수학적 예술에 관한 9개의 장, pp. 71 ff를 참조하십시오.
- ^ Kangshen Shen; John N. Crossley; Anthony Wah-Cheung Lun (1999). The nine chapters on the mathematical art: companion and commentary. Oxford University Press. p. 488. ISBN 0-19-853936-3.
- ^ 특히 리지민; 참조.
- ^ Chen, Cheng-Yih (1996). "§3.3.4 Chén Zǐ's formula and the Chóng-Chã method; Figure 40". Early Chinese work in natural science: a re-examination of the physics of motion, acoustics, astronomy and scientific thoughts. Hong Kong University Press. p. 142. ISBN 962-209-385-X.
- ^ Wen-tsün Wu (2008). "The Gougu theorem". Selected works of Wen-tsün Wu. World Scientific. p. 158. ISBN 978-981-279-107-8.
인용된 작품
- Bell, John L. (1999). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development. Kluwer. ISBN 0-7923-5972-0.
- archive.org 의 온라인 텍스트
- Heath, Sir Thomas (1921). "The 'Theorem of Pythagoras'". A History of Greek Mathematics (2 Vols.) (Dover Publications, Inc. (1981) ed.). Clarendon Press, Oxford. pp. 144 ff. ISBN 0-486-24073-8.
- Libeskind, Shlomo (2008). Euclidean and transformational geometry: a deductive inquiry. Jones & Bartlett Learning. ISBN 978-0-7637-4366-6. 이 고등학교 기하학 교과서는 이 WP 기사의 많은 주제를 다루고 있습니다.
- Loomis, Elisha Scott (1940). The Pythagorean Proposition (2nd ed.). Ann Arbor, Michigan: Edwards Brothers. ISBN 9780873530361. 1968년 전국 수학 교사 협의회에서 재발행. 저품질 스캔은 교육 자원 정보 센터인 ERIC ED037335에 의해 온라인에 게시되었습니다.
- Maor, Eli (2007). The Pythagorean Theorem: A 4,000-Year History. Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
- Neugebauer, Otto (1969). The exact sciences in antiquity. Vol. 9 (Republication of 1957 Brown University Press 2nd ed.). Courier Dover Publications. pp. 1–191. ISBN 0-486-22332-9. OCLC 638685764. PMID 14884919.
{{cite book}}:journal=무시됨(도움말) - 롭슨, 엘리너, 재클린 스테달, 에드스, 옥스퍼드 수학사 핸드북, 옥스퍼드: 옥스포드 대학 출판부, 2009. pp. vii + 918. ISBN 978-0-19-921312-2.
- Stillwell, John (1989). Mathematics and Its History. Springer-Verlag. ISBN 0-387-96981-0. Also ISBN 3-540-96981-0.
- Swetz, Frank; Kao, T. I. (1977). Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China. Pennsylvania State University Press. ISBN 0-271-01238-2.
- van der Waerden, Bartel Leendert (1983). Geometry and Algebra in Ancient Civilizations. Springer. ISBN 3-540-12159-5.
Pythagorean triples Babylonian scribes van der Waerden.
외부 링크
- 프루프위키의 피타고라스 정리
- Euclid (1997) [c. 300 BC]. David E. Joyce (ed.). Elements. Retrieved 2006-08-30. 자바 기반의 대화형 도형이 있는 HTML에서.
- "Pythagorean theorem". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
- 히스토리 주제: 바빌론 수학에서 피타고라스의 정리
- 대화형 링크:
- 유투브에서 피타고라스 정리 물 데모
- 피타고라스 정리(칼로 잘라낸 70개 이상의 증명)
- Weisstein, Eric W. "Pythagorean theorem". MathWorld.


 , 그 변의 길이는 a, b, c이고 빗변의 길이는 c입니다. 오른쪽 사각형은 사각형의 모서리가 삼각형에서 직각의 모서리와 대응하도록 배치되어 변의 길이가 c인 정사각형을 중앙에 형성합니다. 각 외부 사각형의 면적은
, 그 변의 길이는 a, b, c이고 빗변의 길이는 c입니다. 오른쪽 사각형은 사각형의 모서리가 삼각형에서 직각의 모서리와 대응하도록 배치되어 변의 길이가 c인 정사각형을 중앙에 형성합니다. 각 외부 사각형의 면적은 ,
, 
































































 R의n 직교 벡터라고 합니다. 정점이
R의n 직교 벡터라고 합니다. 정점이 



![{\displaystyle {\begin{aligned}\left\|\mathbf {v} +\mathbf {w} \right\|^{2}&=\langle \mathbf {v+w} ,\ \mathbf {v+w} \rangle \\[3mu]&=\langle \mathbf {v} ,\ \mathbf {v} \rangle +\langle \mathbf {w} ,\ \mathbf {w} \rangle +\langle \mathbf {v,\ w} \rangle +\langle \mathbf {w,\ v} \rangle \\[3mu]&=\left\|\mathbf {v} \right\|^{2}+\left\|\mathbf {w} \right\|^{2},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c30b0575230c350ae41528af64dbe6ed55df988)



 m차원(1차원의 길이, 2차원의 면적, 3차원의 부피 등) 단위입니다.
m차원(1차원의 길이, 2차원의 면적, 3차원의 부피 등) 단위입니다. n차원 유클리드 공간의 하나 이상의 평행 m차원 평면에 있는 하나 이상의 중첩되지 않는 m차원 객체의 집합입니다.
n차원 유클리드 공간의 하나 이상의 평행 m차원 평면에 있는 하나 이상의 중첩되지 않는 m차원 객체의 집합입니다.

 m차원 좌표
m차원 좌표 
 m차원 객체가 투영되는 n차원 공간(
m차원 객체가 투영되는 n차원 공간(

















