리간드 장 이론

Ligand field theory

LFT(Ligand Field Theory)[1][2][3]는 배위 복합체의 결합, 궤도 배치 및 기타 특성을 설명합니다.그것은 전이 금속 복합체에 분자 궤도 이론의 적용을 나타냅니다.전이 금속 이온은 5번째, 1번째(n+1)s 및 3번째(n+1)p의 오비탈로 구성된 9개의 원자가 원자 오비탈을 가진다.이러한 오비탈은 리간드와 결합 상호작용을 형성하기에 적절한 에너지이다.LFT 분석은 복합체의 형상에 크게 의존하지만, 대부분의 설명은 6개의 배위자가 금속에 대해 조정되는 8면체 복합체를 설명하는 것으로 시작합니다.다른 복합체는 결정장 이론을 [4]참고하여 설명할 수 있다.

역사

리간드 장 이론은 분자 궤도 이론과 전이 금속 복합체에서 금속 d 오비탈의 퇴행성 손실을 설명하는 결정장 이론의 결합에서 비롯되었습니다.존 스탠리 그리피스와 레슬리[5] 오르겔은 리간드장이론을 그러한 복합체의 보다 정확한 기술이라고 옹호했지만, 이 이론은 존 하스브룩 반 블렉의 자성에 대한 연구로 1930년대에 시작되었다.그리피스와 오르겔은 결정장 이론에서 확립된 정전 원리를 용액에서 전이 금속 이온을 기술하기 위해, 분자 궤도 이론을 사용하여 금속-배위자 상호작용의 차이를 설명함으로써, 결정장 안정화 및 전이 금속 복합체의 가시 스펙트럼과 같은 관찰을 설명했습니다.그들의 논문에서, 그들은 용액에서 전이 금속 착체의 색 차이의 주요 원인이 불완전한 d 궤도 [5]서브셸이라고 제안했다.즉, 전이 금속의 점유되지 않은 d 오비탈은 결합에 참여하며, 이는 용액에서 흡수되는 색상에 영향을 미칩니다.리간드 장 이론에서 다양한 d 오비탈은 인접한 리간드 [5]장에 둘러싸여 있을 때 다른 영향을 받고 리간드와의 상호작용 강도에 따라 에너지가 상승 또는 감소한다.

본딩

γ-module(본딩)

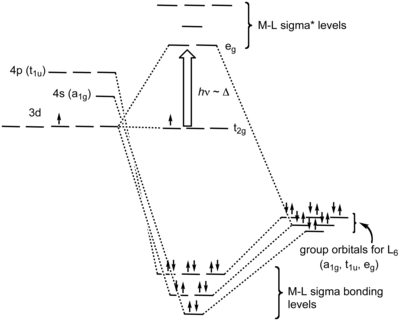
8면체 복합체에서 배위에 의해 생성된 분자 궤도는 금속상의 d-오비탈에 6개의 γ-공여 배위자 각각에 의해 2개의 전자가 기증된 결과인 것으로 볼 수 있다.팔면체 복합체에서 리간드는 x축, y축 및 z축을 따라 접근하기 때문에 이들의 γ대칭 궤도는 d축z2 및x2−y2 d축과 결합 및 반결합 조합을 형성한다.dxy, dxz 및yz d 오비탈은 비결합 오비탈로 남습니다.금속의 s 및 p 궤도와의 약한 결합(및 반결합) 상호작용도 일어나 총 6개의 결합(및 6개의 반결합) 분자 궤도를 만든다.

8면체 복합체의 γ 결합을 요약하는 리간드-장 체계 [Ti(HO2)]63+

분자대칭 측면에서, 리간드(각 리간드로부터 1개씩)의 6개의 단일 쌍 오비탈은 때때로 리간드 그룹 오비탈(LGOs)이라고도 불리는 6개의 대칭 적응 선형 결합(SALCs)을 형성한다.이 스팬이 a, t1u, e인1gg 축소할 수 없는 표현.금속은 또한 이러한 환원 불가능한 표현에 걸쳐 6개의 원자가 궤도를 가지고 있다. 즉, s 오비탈은 a1g, p 오비탈 세트는 t1u, dz2x2−y2 오비탈과 d 오비탈은 e로g 분류된다.6개의 γ 결합 분자 오비탈은 동일한 대칭의 금속 오비탈과 리간드 SALC의 조합에서 발생한다.

γ-module (파이 본딩)

팔면체 복합체에서의 γ결합은 γ결합에 사용되지 않는 임의의 리간드 p-결합을 통해, 그리고 리간드 상에 존재하는 임의의 β 또는* β 분자궤도를 통해 두 가지 방법으로 일어난다.

통상적인 분석에서는 금속의 p-오비탈은 δ결합에 이용되기 때문에(또한 리간드 p 또는 θ 또는 θ* 오비탈과 중복되는 잘못된 대칭을 가진다), δ 상호작용은 적절한 금속 d-오비탈, 즉xy d, d와xzyz d와 함께 일어난다.이것들은 δ 결합만 이루어졌을 때 비결합이 되는 궤도입니다.

카보닐(CO) 리간드를 사용한 γ 백본드의 예.

배위 복합체에서의 중요한 δ결합 중 하나는 금속과 리간드 간의 결합이며, δ 백본딩이라고도 합니다.배위자의 LUMO(최저 빈 분자 궤도)가 반결합 δ* 궤도일 때 발생한다.이러한 궤도는 결합 궤도를 형성하기 위해 결합하는xy d, dxz 및yz d 궤도에 에너지가 가깝다(즉, 앞서 언급한 d 궤도 세트보다 낮은 에너지의 궤도).대응하는 반결합 오비탈은 δ결합으로부터의 반결합 오비탈보다 에너지가 높기 때문에 새로운 δ결합 오비탈이 금속 d-오비탈로부터의 전자로 채워진 후에는 δ가O 증가하여 배위자와 금속 사이의 결합이 강화된다.리간드는 δ분자궤도에서* 전자로 끝나므로 리간드 내의 대응하는 δ결합이 약해진다.

배위결합의 다른 형태는 리간드와 금속의 결합이다.이 상황은 리간드의 θ-대칭성 p 또는 θ 오비탈이 채워질 때 발생한다.이들은 금속의xy d, dxz 및 dyz 오비탈과 결합하고 그 결과 발생하는 γ-대칭 결합 오비탈에 전자를 공급한다.금속-리간드 결합은 이 상호작용에 의해 다소 강화되지만, 리간드-금속 결합에 의한 상보적인 반결합 분자 오비탈은 γ 결합에 의한 반결합 분자 오비탈보다 에너지가 높지 않다.그러나 그것은 금속 d-오비탈의 전자들로 채워져 복합체의 가장 높은 점유율 분자 궤도(HOMO)가 된다.따라서 리간드와 금속의 결합이 일어나면 δ가O 감소한다.

금속-배위자 결합에서 발생하는 더 큰 안정화는 금속 이온에서 배위자 쪽으로 음전하가 공급됨으로써 발생합니다.이를 통해 금속은 δ 결합을 보다 쉽게 받아들일 수 있습니다.리간드-금속간 γ결합과 금속-리간드 γ결합의 조합은 서로 강화되기 때문에 시너지 효과이다.

6개의 리간드는 각각 θ-대칭의 2개의 궤도를 가지므로 총 12개의 리간드가 있다.대칭에 적응한 선형 조합은 4개의 3중으로 축퇴할 수 없는 표현으로 나뉘는데, 그 중 하나는 t대칭이다2g.금속의 d, dxz 및 dyz 궤도도 이러한 대칭을xy 가지며, 따라서 중심 금속과 6개의 리간드 사이에 형성된 γ 결합도 대칭을 가진다(이들 γ 결합은 t 대칭을 가진2g 두 세트의 궤도 중첩에 의해 형성되기 때문이다).

고회전 및 저회전 및 분광화학 시리즈

주요 기사: 스핀 상태(d전자)
참고 항목: 자기 화학

형성된 6개의 결합 분자 궤도는 배위자의 전자로 채워지고, 금속 이온의 d-오비탈의 전자는 비결합을 차지하고, 경우에 따라서는 반결합 MO를 차지합니다.후자의 두 가지 유형의 MO 사이의 에너지 차이는 δO (O는 8면체를 의미함)라고 불리며, 중심 원자의 d-오비탈과 배위자 궤도 사이의 δ-상호작용의 성질에 의해 결정된다.위와 같이 γ-공여 리간드는 δ가O 작아 약장 리간드 또는 저장 리간드라고 하며, γ-수용 리간드는 δ의O 큰 값으로 이어져 강장 리간드 또는 고장 리간드라고 한다.γ-공여체도 γ-acceptor도 아닌 리간드는 중간값으로 δO 값을 구한다.

δ의O 크기에 따라 d4 - d7 이온의 전자구조가 결정된다.이러한 d전자 구성을 가진 금속의 복합체에서는 비결합 및 반결합 분자 궤도는 두 가지 방법으로 채워질 수 있다. 하나는 반결합 궤도에 채워지기 전에 가능한 한 많은 전자를 비결합 궤도에 넣는 것이고, 다른 하나는 가능한 한 많은 비결합 전자를 넣는 것이다.전자는 로우 스핀이라고 불리는 반면 후자는 하이 스핀이라고 불립니다.소량의 δ는O 전자를 짝짓지 않을 때의 에너지 이득으로 극복할 수 있어 고스핀으로 이어진다.그러나 δ가O 크면 그에 비해 스핀쌍 에너지는 무시할 수 있게 되어 스핀이 낮은 상태가 된다.

스펙트럼 화학 시리즈는 생성되는 분할 δ의 크기에 따라 정렬된 경험적으로 파생된 배위자 목록입니다.저장 리간드는 모두 γ-공여체(I− 등), 고장 리간드는 γ-수용체(CN, CO 등−)이며, HO3, NH 등의2 리간드는 둘 다 중간이 아님을 알 수 있다.

I−3 < Br− < S2− < Cl−− < No3−3− < N− < OH−242−2 < HO− < NCS3 < CHCN < py ( pyridine ) < NH < en ( 에틸렌디아민) < bipyridine ( 2 , 2 ' - 비피리딘) < pen ( 1,10 - penanthro ） < PPHline2−3− <

「 」를 참조해 주세요.

레퍼런스

  1. ^ 발하우젠, 칼 요한."Ligand Field Theory (Ligand Field Theory 입문), 1962년 뉴욕 McGraw-Hill Book Co.
  2. ^ Griffith, J.S. (2009). The Theory of Transition-Metal Ions (re-issue ed.). Cambridge University Press. ISBN 978-0521115995.
  3. ^ Schléfer, H. L.; Gliemann, G. "Ligand Field Theory의 기본 원리" 와일리 인터사이언스:뉴욕; 1969년
  4. ^ G. L. 미슬러와 D.A. Tarr "유기화학" 제3판, Pearson/Prentice Hall 출판사, ISBN 0-13-035471-6.
  5. ^ a b c 그리피스, J.S., L.E.오르골 '리간드 필드론'Q. 화학 목사님 Soc. 1957, 11, 381-393

외부 링크