수정장 이론
Crystal field theory결정장 이론(CFT)은 주변 전하 분포(음이온 이웃)에 의해 생성되는 정전기장으로 인해 대개 d 또는 f궤도인 전자 궤도 상태의 퇴화현상이 깨지는 것을 설명한다. 이 이론은 전환 금속 조정 복합체, 특히 광학 스펙트럼(색상)의 다양한 분광법을 설명하기 위해 사용되어 왔다. CFT는 전이 금속 복합체의 일부 자기성, 색상, 수화 엔탈피, 스피넬 구조를 성공적으로 설명하지만, 결합을 설명하려 하지 않는다. CFT는 1930년대에 물리학자인 한스 베테와[1] 존 하스브루크 반블렉에[2] 의해 개발되었다. CFT는 이후 분자 궤도 이론과 결합되어 전이 금속 단지의 화학적 결합 과정에 대한 통찰력을 전달하는 보다 현실적이고 복잡한 리간드 장 이론(LFT)을 형성했다.
수정장 이론 개요
수정장 이론에 따르면 전이 금속과 리간드 사이의 상호작용은 리간드의 비결합 전자에 대한 양전하 금속 양이온과 음전하 사이의 끌어당김에서 발생한다. 이 이론은 리간드로 구성된 점 전하의 배열로 둘러싸인 후 퇴화된 5개의 d-orbitals의 에너지 변화를 고려하여 개발된다. 리간드가 금속 이온에 접근하면 리간드에서 나온 전자는 일부 d-orbital에 더 가깝고 다른 전자로부터 멀리 떨어져 퇴행성을 상실하게 된다. d-orbitals의 전자와 리간드의 전자는 유사 전하 사이의 반발 때문에 서로 밀어낸다. 따라서 리간드에 더 가까운 d전자는 더 멀리 떨어져 있는 d-orbitals의 에너지보다 더 높은 에너지를 가질 것이며, 이로 인해 d-orbitals가 에너지에서 갈라지게 된다. 이 분할은 다음 요인의 영향을 받는다.
- 금속 이온의 성질
- 금속의 산화 상태 산화 상태가 높을수록 구형장에 비해 더 큰 분할이 발생한다.
- 금속 이온 주위의 리간드 배열
- 금속의 조정 번호(즉, 사면체, 팔면체...)
- 금속 이온을 둘러싸고 있는 리간드의 성질 리간드의 효과가 강할수록 높은 에너지와 낮은 에너지 d 그룹의 차이가 커진다.
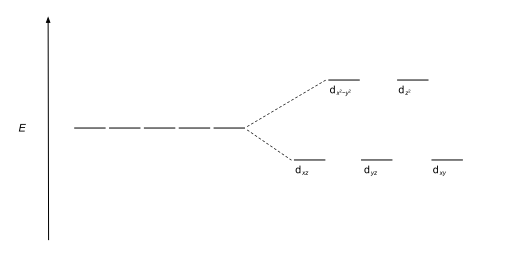
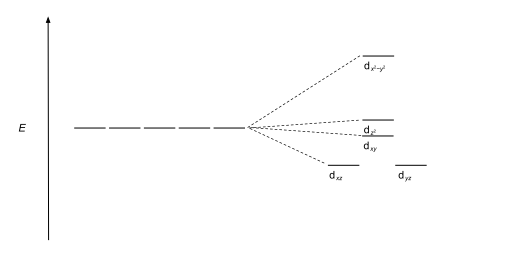
가장 흔한 형태의 콤플렉스는 8각형이며, 6개의 리간드가 금속 이온 주위의 8각형의 정점을 형성한다. 8면체 대칭에는 d-orbitals는 에너지 차이가 dxy, dxz과dyz 궤도 에너지에 더 높은 에너지가 갖게 될 dz2과 dx2-y2보다 더 낮을 것이다Δoct(그crystal-field 분열 매개 변수, 또한 흔히 10Dq 10번을 이 가리키는"quanta의 미분"[3][4]), 왜냐하면 전자는 그룹과 두세트로 갈라진다.의 훨씬 깊숙한 곳에서 후자보다 리간드가 더 강하기 때문에 거부감이 적다. 세 개의 낮은 에너지 궤도를 총칭하여 t라고2g 하고, 두 개의g 높은 에너지 궤도를 e라고 한다. 이 라벨들은 분자 대칭 이론에 기초한다: 그것들은 팔면체 점 그룹의 수정 불가능한 표현들의 이름이다. (Ohh 문자표 참조) 전형적인 궤도 에너지 다이어그램은 아래 High-spin과 Low-spin 섹션에 제시되어 있다.
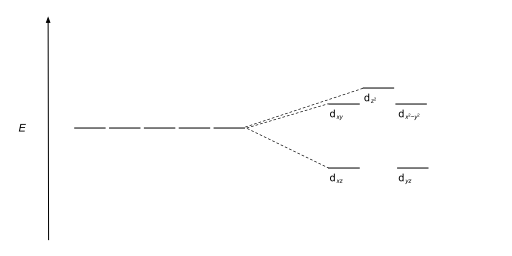
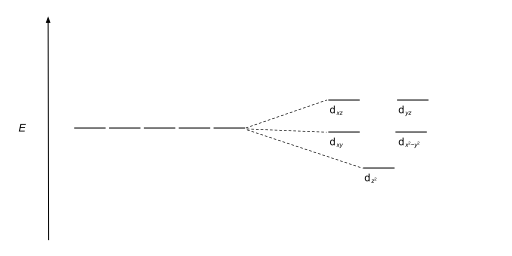
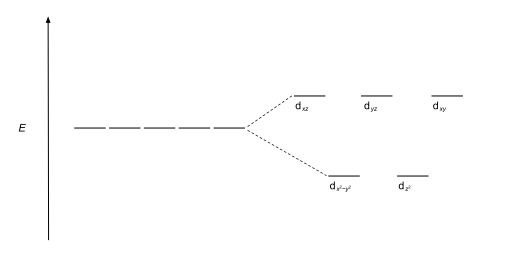
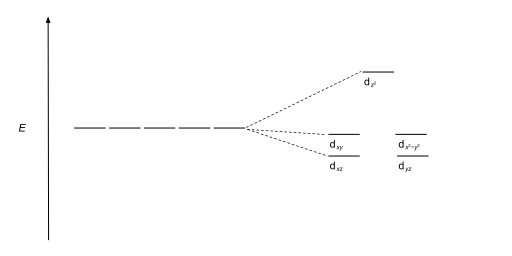
사면체 복합체는 두 번째로 흔한 유형이다; 여기 네 개의 리간드가 금속 이온 주위에 사면체를 형성한다. 사면 결정장 분할에서 d-orbital은 다시 두 그룹으로 나뉘어 에너지 차이가 Δ이다tet. 낮은 에너지 궤도들은 d와z2 d가x2-y2 될 것이고, 높은 에너지 궤도들은 팔면체의 경우와 반대되는 dxy, dxz, d가yz 될 것이다. 더욱이 사면 대칭에 있는 리간드 전자는 d-orbital을 직접 향하지 않기 때문에 에너지 분할은 8면체 사례보다 더 낮을 것이다. 정사각형 평면 및 기타 복잡한 기하학적 구조도 CFT로 설명할 수 있다.
둘 이상의 궤도 집합 사이의 간격 Δ의 크기는 복합체의 리간드와 기하학을 포함한 몇 가지 요인에 따라 달라진다. 어떤 리간드는 항상 Δ의 작은 값을 생성하는 반면, 다른 리간드는 항상 큰 Δ의 값을 산출한다. 이면의 이유는 리간드 장 이론으로 설명할 수 있다. 분광화학 시리즈는 그들이 생산하는 분할 Δ의 크기에 의해 주문된 경험적으로 파생된 리간드의 목록이다(작은 Δ to large Δ에 대한 Δ; 이 표도 참조).
I− < Br− < S2− > SCN− (S–bonded) > Cl−3− < N3− < F− < OH− < CO242− < HO2 < NCS− (N–bonded))> < CHCN3 < py < py3 > py < en < 2,2>-비피리딘 <NO2− > PH3 < CN− C.
가장 많이 갈라지는 리간드는 리간드 백본딩에 금속을 관여할 수 있는 것이라는 점을 유념하는 것이 유용하다.
또한 금속의 산화 상태는 높은 에너지 수준과 낮은 에너지 수준 사이의 Δ의 크기에 기여한다. 주어진 금속의 산화 상태가 증가함에 따라 Δ의 크기는 증가한다. 충전 밀도의 차이로 인해 리간드가 V 이온보다2+ V3+ 이온에 더 가까워질 수 있기 때문에 V3+ 단지는 주어진 리간드 집합에 대한 V 복합체보다2+ Δ가 더 클 것이다. 리간드와 금속 이온 사이의 거리가 작을수록 Δ가 더 커지는데, 이는 리간드와 금속 전자가 서로 더 가까워지고 따라서 더 많이 밀어내기 때문이다.
하이 스핀 및 로우 스핀
d-orbitals의 큰 분열 Δ를 유발하는 리간드를 분광화학 계열의 CN과− CO와 같은 강장 리간드라고 한다. 이러한 리간드가 있는 콤플렉스에서는 높은 에너지 궤도에 전자를 넣는 것은 바람직하지 않다. 따라서 상위 집합의 모집단이 Aufbau 원칙에 따라 시작되기 전에 하위 에너지 궤도들이 완전히 채워진다. 이와 같은 콤플렉스를 "로우 스핀"이라고 한다. 예를 들어 NO는2− 강장 리간드로 큰 Δ를 산출한다. 5 d 전자를 가진 팔면 이온[Fe(NO2)]63−은 우측에 5개의 전자가 모두 t2g 레벨에 있는 팔면 분할도를 표시할 것이다. 따라서 이 낮은 회전 상태는 헌드의 규칙을 따르지 않는다.
반대로 d-orbitals의 작은 분열 Δ를 일으키는 리간드(I−, Br− 등)를 약장 리간드라고 한다. 이 경우 동일한 궤도상에 있는 두 전자가 서로 밀어내기 때문에 동일한 저에너지 궤도상에 두 전자를 넣는 것보다 더 높은 에너지 세트에 전자를 넣는 것이 더 쉽다. 그래서 훈드의 규칙에 따라 5개의 d-orbital에 각각 1개의 전자를 넣고, 어떤 쌍이 생기기도 전에 "하이 스핀" 콤플렉스가 형성된다. 예를 들어 Br은− 약한 장 리간드로 작은 Δ를oct 산출한다. 그래서, 이온[FeBr6]3−은 다시 5개의 d-전자를 가지고, 5개의 궤도 모두가 단독으로 점유되는 8각 분할도를 가지고 있을 것이다.
낮은 스핀 분할이 발생하기 위해서는 이미 단독으로 점유된 궤도상에 전자를 배치하는 에너지 비용은 추가 전자를 Δ의 에너지 비용으로 eg 궤도 안에 넣는 비용보다 적어야 한다. 위에서 언급한 바와 같이 e는g 팔면체 복합체에서 t보다2g 에너지가 높은 d와z2 d를x2-y2 가리킨다. 만약 두 전자를 쌍으로 만드는 데 필요한 에너지가 Δ보다 크면, 전자 하나를g e에 놓는 에너지 비용인 높은 스핀 분할이 발생한다.
사면 금속 복합체(4개의 리간드)에 대한 에너지 분할 결정장을 Δ라고tet 하며, 대략 4/9 Δoct (동일한 금속 및 동일한 리간드에 대한)와 같다. 따라서 두 개의 전자를 쌍으로 만드는 데 필요한 에너지는 일반적으로 더 높은 에너지 궤도에 전자를 배치하는 데 필요한 에너지보다 높다. 따라서 사면체 복합체는 대개 고경련이다.
이러한 분할도를 사용하면 조정 화합물의 자기 성질을 예측하는 데 도움이 될 수 있다. 분할 도표에 손상된 전자가 있는 화합물은 파라마그네틱이 되어 자기장에 이끌리게 되며, 분할 도표에 손상된 전자가 없는 화합물은 직경이 되어 자기장에 의해 약하게 반발하게 된다.
결정장 안정화 에너지
결정장 안정화 에너지(Crystal field stabilization energy, CFSE)는 리간드 집합에 의해 생성되는 결정장에 전이 금속 이온을 배치함으로써 발생하는 안정성이다. d-orbital을 리간드(위에서 기술한 바와 같이)장에서 분할할 때, 5개의 d-orbital이 모두 퇴행하는 barycenter라고 알려진 구면장에 관해서 그 중 일부는 이전보다 에너지가 낮아지기 때문에 발생한다. 예를 들어, 팔면체의 경우, t2g 세트는 중간의 궤도보다 에너지가 더 낮아진다. 그 결과, 이러한 궤도들을 점유하고 있는 전자가 있다면, 금속 이온은 CFSE라고 알려진 양만큼 바이센터 대비 리간드 장에서 더 안정적이다. 반대로g e 궤도(팔면체 케이스의 경우)는 바이센터보다 에너지가 더 높기 때문에, 여기에 전자를 넣으면 CFSE의 양이 줄어든다.
팔면장 d-orbitals의 분할이 Δ인oct 경우,5 3 t2g 궤도들은 / Δ에oct 의해 barycenter에 상대적으로 안정화되고, e 5궤도들은goct / Δ에 의해 불안정해진다. 예를 들어, 페이지 위에 더 위에 표시된 두 d 구성을5 고려한다. 저 스핀(상단) 예는 t 궤도상에2g 5개의 전자가 있으므로 총 CFSE는 5 x / 5Δoct = 2Δ이다oct. 고 스핀(하단) 예제에서 CFSE는 (3 x / 5Δoct) - (2 x / 5Δoct) = 0 - 이 경우, 하부 궤도에서의 전자에 의해 발생하는 안정화는 상궤도 전자의 불안화 효과에 의해 취소된다.
광학 특성
많은 조정 콤플렉스의 광학적 특성(흡수 및 방출 스펙트럼의 세부사항)은 크리스탈 필드 이론으로 설명할 수 있다. 그러나 종종 금속 단지의 더 깊은 색은 더욱 강렬한 전하 전달 배설물에서 발생한다.[5]
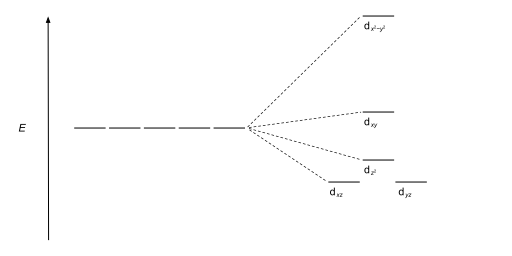
지오메트리 및 결정장 분할 다이어그램
| 이름 | 모양 | 에너지 다이어그램 |
|---|---|---|
| 팔면체 |  | |
| 오각형 두피라미드 |  | |
| 정사각형 항정신병 | 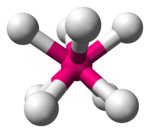 | |
| 사각 평면체 |  | |
| 사각 피라미드 | 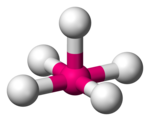 | |
| 사면체 | 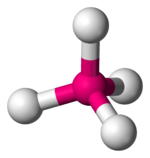 | |
| 삼위일체 |  |
참고 항목
참조
- ^ Bethe, H. (1929). "Termaufspaltung in Kristallen". Annalen der Physik (in German). 395 (2): 133–208. Bibcode:1929AnP...395..133B. doi:10.1002/andp.19293950202. ISSN 1521-3889.
- ^ Van Vleck, J. (1932). "Theory of the Variations in Paramagnetic Anisotropy Among Different Salts of the Iron Group". Physical Review. 41 (2): 208–215. Bibcode:1932PhRv...41..208V. doi:10.1103/PhysRev.41.208.
- ^ Penney, William G.; Schlapp, Robert (1932). "The Influence of Crystalline Fields on the Susceptibilities of Salts of Paramagnetic Ions. I. The Rare Earths, Especially Pr and Nd". Physical Review. 41 (2): 194–207. Bibcode:1932PhRv...41..194P. doi:10.1103/PhysRev.41.194. ISSN 0031-899X.
- ^ Schlapp, Robert; Penney, William G. (1932). "Influence of Crystalline Fields on the Susceptibilities of Salts of Paramagnetic Ions. II. The Iron Group, Especially Ni, Cr and Co". Physical Review. 42 (5): 666–686. Bibcode:1932PhRv...42..666S. doi:10.1103/PhysRev.42.666. ISSN 0031-899X.\
- ^ G. L. Miessler와 D. A. Tarr "In 유기 화학" 2차 Ed. (Prentice Hall 1999), p.379 ISBN 0-13-841891-8.
추가 읽기
- Housecroft, C. E.; Sharpe, A. G. (2004). Inorganic Chemistry (2nd ed.). Prentice Hall. ISBN 978-0-13-039913-7.
- Miessler, G. L.; Tarr, D. A. (2003). Inorganic Chemistry (3rd ed.). Pearson Prentice Hall. ISBN 978-0-13-035471-6.
- Orgel, Leslie E. (1960). An introduction to transition-metal chemistry: Ligand-Field theory. Methuen. ISBN 978-0416634402.
- Shriver, D. F.; Atkins, P. W. (2001). Inorganic Chemistry (4th ed.). Oxford University Press. pp. 227–236. ISBN 978-0-8412-3849-7.
- Silberberg, Martin S (2006). Chemistry: The Molecular Nature of Matter and Change (4th ed.). New York: McGraw Hill Company. pp. 1028–1034. ISBN 978-0-8151-8505-5.
- Zumdahl, Steven S (2005). Chemical Principles (5th ed.). Houghton Mifflin Company. pp. 550–551, 957–964. ISBN 978-0-669-39321-7.
외부 링크
- E. 파바리니, E. 코흐, F.의 크리스탈-필드 이론, 빡빡한 바인딩 방법, 얀-텔러 효과. 앤더스와 M. 자렐(에드): 상관 전자: 모델에서 재료로 쥴리히 2012, ISBN 978-3-89336-796-2
- Citizendium.org의 수정장 이론(논문)