항공기 비행 역학

비행 역학은 3차원에서 항공기 방향과 제어에 대한 과학입니다.세 가지 중요한 비행 역학 매개 변수는 차량의 무게 중심(cg)에 대한 3차원 회전 각도(피치, 롤링 및 요)입니다.이것들은 일반적으로 항공기 자세로 알려져 있으며, 주로 정상적인 비행에서 대기 프레임에 상대적이지만 이륙 또는 착륙 중 또는 낮은 고도에서 작동할 때 지형에 상대적이기도 합니다.자세의 개념은 고정익 항공기에 한정되지 않고 헬리콥터와 같은 회전 항공기와 조종기에도 적용되며, 자세 설정과 제어에 관련된 비행 역학이 완전히 다릅니다.

제어 시스템은 cg를 기준으로 차량의 방향을 조정합니다.제어 시스템은 편향될 때 항공기를 피치, 롤링 및 요로 회전시키는 CG에 대한 모멘트(또는 에일러론에서 커플링)를 생성하는 제어 표면을 포함합니다.예를 들어, 피칭 모멘트는 cg의 전방 또는 후방 거리에 가해지는 힘에서 발생하여 항공기가 위 또는 아래로 피칭되도록 합니다.

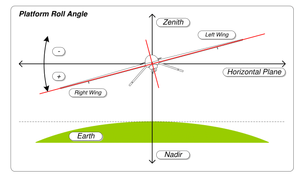
롤, 피치 및 요는 정의된 안정적인 비행 평형 상태에서 시작하는 각 축 주위의 회전을 말합니다.평형 롤 각도는 윙 레벨 또는 제로 뱅크 각도로 알려져 있습니다.

가장 일반적인 항공 규칙에서는 롤을 우현(오른쪽) 날개를 아래로 한 상태에서 양의 세로 축에 대해 작용하는 것으로 정의합니다.요는 수직 차체 축에 대한 것으로, 노즈와 우현이 양의 위치에 있습니다.피치는 대칭의 세로 면에 수직인 축에 대한 것으로, 양의 코가 ^[1]위로 향합니다.

고정익 항공기는 공격각(AOA)을 증가 또는 감소시켜 노즈 업 또는 다운으로 투구할 때 날개에 의해 발생하는 양력을 증가 또는 감소시킵니다.롤 각도는 고정익 항공기에서 뱅크 각도라고도 하며, 일반적으로 수평 비행 방향을 변경하기 위해 "뱅크"합니다.항공기는 측면 미끄러짐 각도를 0에 가깝게 유지하는 것이 유리하도록 기수에서 꼬리까지 유선형화됩니다. 그러나 항공기는 착륙 중 항력과 하강 속도를 증가시키기 위해 의도적으로 "측면 미끄러짐"될 수 있으며, 횡풍 착륙 및 비대칭 ^[2]전력으로 비행 중에도 활주로 방향과 동일하게 비행할 수 있습니다.

요우

피치

굴리다

요 또는 헤딩 각도 정의^[3]

피치 각도 정의^[3]

롤 각도 정의^[3]

소개

참조 프레임

3개의 오른손잡이 데카르트 좌표계는 비행 역학에서 자주 사용됩니다.첫 번째 좌표계는 지구의 기준 프레임에 고정된 원점을 가지고 있습니다.

지구 틀
- 원점 - 임의, 지구 표면을 기준으로 고정
- x축_E - 북쪽 방향의 양의 값
- y축_E - 동쪽 방향에서 양의 값
- z축 - 지구의 중심을 향해 양의 값을_E 나타냄

많은 비행 역학 응용 분야에서 지구 프레임은 평평한_E x, y_E 평면을 가진 관성계로 가정되지만, 지구 프레임은 지구의 중심에 원점이 있는 구형 좌표계로 간주될 수도 있습니다.

다른 두 개의 기준 프레임은 차체에 고정되어 있으며, 원점이 항공기를 따라 이동하며, 일반적으로 무게 중심에 있습니다.오른쪽에서 왼쪽으로 대칭인 항공기의 경우 프레임은 다음과 같이 정의할 수 있습니다.

차체 프레임
- 원점 - 비행기 무게중심
- x축_b - 항공기 대칭면에서 항공기 코 바깥쪽의 양의 값
- z축_b - 항공기의 대칭면에서 x축에_b 수직, 항공기 아래의 양의
- y축_b - x_b,z-평면에_b 수직, 우측 규칙에 의해 결정된 양의 값(오른쪽 날개 바깥쪽의 양의 값)
바람틀
- 원점 - 비행기 무게중심
- x축_w - 공기를 기준으로 한 항공기의 속도 벡터 방향에서 양의 값
- z축_w - 항공기의 대칭면에서 x축에_w 수직, 항공기 아래의 양의
- y축_w - x_w,z-평면에_w 수직, 오른손 법칙에 의해 결정되는 양의 값(직각, 오른쪽에 양의 값)

비대칭 항공기는 차체 고정 프레임이 유사하지만 x축과 z축의 정확한 방향을 선택하려면 서로 다른 규칙을 사용해야 합니다.

지구 프레임은 항공기의 번역 및 회전 운동학을 표현하기에 편리한 프레임입니다.지구 프레임은 특정 가정 하에서 관성으로 근사할 수 있다는 점에서도 유용합니다.또한 항공기에 작용하는 하나의 힘인 무게가 +z_E 방향으로 고정됩니다.

원점과 축이 항공기에 대해 고정되어 있기 때문에 차체 프레임이 종종 관심을 끌 수 있습니다.이것은 지구와 차체 프레임의 상대적인 방향이 항공기 자세를 설명한다는 것을 의미합니다.또한 추력의 방향은 일반적으로 차체 프레임에 고정되어 있지만, 일부 항공기는 예를 들어 추력 벡터링을 통해 이 방향을 변경할 수 있습니다.

윈드 프레임은 항공기에 작용하는 공기역학적 힘과 모멘트를 표현하기에 편리한 프레임입니다.특히, 순 공기역학적 힘은 -x_w 방향의 항력과_w -z 방향의 승강력으로 윈드 프레임 축을 따라 구성 요소로 나눌 수 있습니다.

각도 이름을 기억하는 니모닉

기준 프레임을 정의하는 것 외에도 기준 프레임의 상대적 방향을 결정할 수 있습니다.상대 방향은 다음과 같은 다양한 형태로 표현될 수 있습니다.

세 개의 기준 프레임과 관련된 다양한 오일러 각도는 비행 역학에 중요합니다.많은 오일러 각도 규칙이 존재하지만 아래에 제시된 모든 회전 시퀀스는 z-y'-x" 규칙을 사용합니다.이 규칙은 일반적으로 오일러 각도라고 하는 타이트-브라이언 각도 유형에 해당합니다.이 규칙은 아래에서 접지 프레임을 기준으로 차체 프레임 방향을 설명하는 롤, 피치 및 요 오일러 각도에 대해 자세히 설명합니다.오일러 각도의 다른 세트는 아래에서 유추하여 설명합니다.

변환(글루어 각도)

접지 프레임에서 차체 프레임으로

먼저 Z축을_E_E 중심으로 지구_E 프레임 축 x와 y를 요 각도 θ만큼 회전시킵니다.따라서 축이 x',y',z'로 표시된 중간 기준 프레임이 생성됩니다. 여기서 z'=z_E.
둘째, x', z'축을 y'축을 중심으로 피치각θ만큼 회전시킵니다.따라서 축이 x",y",z"로 표시된 다른 중간 기준 프레임이 생성됩니다. 여기서 y"=y'.
마지막으로 y" 및 z" 축을 롤 각도 θ만큼 x" 축 주위로 회전시킵니다.3회 회전 후에 발생하는 기준 프레임이 차체 프레임입니다.

위의 회전 및 축 규칙을 기준으로 합니다.

요 각도 θ: 북쪽과 수평면에 항공기 세로축이 투영되는 각도;
피치각 θ: 항공기 세로축과 수평축 사이의 각도
롤 각도 θ: 요와 피치에 의해 회전한 후 항공기 세로축 주위의 회전.

접지 프레임에서 윈드 프레임으로

헤딩 각도 θ: 속도 벡터의 북쪽과 수평 구성 요소 사이의 각도로, 항공기가 기본 방향을 기준으로 어느 방향으로 이동하는지 설명합니다.
비행 경로 각도 θ: 수평 및 속도 벡터 사이의 각도로, 항공기가 상승 또는 하강 중인지 여부를 설명합니다.
뱅크각 μ: 비행기가 회전하는지 여부를 나타낼 수 있는 속도 벡터 주위의 양력 회전을 나타냅니다.

위에서 설명한 회전을 수행하여 접지 프레임에서 차체 프레임을 얻을 때 각도 사이에는 다음과 같은 유사성이 있습니다.

∙, ∙ (헤드 vs 요)
γ, θ (비행 경로 대 피치)
μ, φ (뱅크 대 롤)

윈드 프레임에서 차체 프레임으로

측면 미끄러짐 각도 β: 속도 벡터와 항공기 세로축의 x_w,y-평면_w 투영 사이의 각도. 항공기 속도에 측면 구성 요소가 있는지 여부를 설명합니다.

공격 각도 α: x_w, y-면과_w 항공기 세로축 사이의 각도 및 무엇보다도 리프트 힘의 크기를 결정하는 데 중요한 변수입니다.

앞서 설명한 회전을 수행하여 접지 프레임에서 차체 프레임을 얻을 때 각도 사이에는 다음과 같은 유사성이 있습니다.

β, γ(입술 대 요)
α, θ (공격 대 투구)
(슬립 = 0)(아무것도 굴리지 않음)

유추

세 개의 기준 프레임 사이에는 다음과 같은 유사성이 있습니다.

요 / 헤딩 / 사이드슬립(Z축, 수직)
피치 / 비행 경로 / 공격 각도(Y축, 날개)
롤 / 뱅크 / 없음 (X축, 노즈)

설계 사례

항공기의 안정성을 분석할 때, 일반적으로 공칭 안정 비행 상태에 대한 섭동을 고려합니다.따라서 분석은 예를 들어 다음을 가정하여 적용됩니다.

직선 및 수평 비행

일정한 속도로 회전합니다.

접근 및 착륙

벗다

공격의 속도, 높이 및 트림 각도는 각 비행 조건에 따라 다르며, 또한 저속 플랩이 전개되고 언더캐리지가 다운되는 등 항공기가 다르게 구성됩니다.

비대칭 설계(또는 상당한 측면 미끄러짐에서 대칭 설계)를 제외하고, 세로 방향 운동 방정식(피치 및 리프트 힘 포함)은 측면 운동(롤 및 요 포함)과 독립적으로 처리할 수 있습니다.

다음은 공칭 직선 및 수평 비행 경로에 대한 섭동을 고려한 것입니다.

분석을 (상대적으로) 단순하게 유지하기 위해 제어 표면은 움직임 내내 고정된 것으로 가정됩니다. 이는 스틱 고정 안정성입니다.스틱이 없는 분석에는 제어 표면의 움직임을 고려하는 추가적인 복잡성이 필요합니다.

또한, 비행은 정지된 공기에서 이루어지는 것으로 가정하고, 항공기는 강체로 취급됩니다.

비행력

세 가지 힘이 비행 중인 항공기에 작용합니다: 무게, 추력, 그리고 공기역학적 힘.

공기역학적 힘

공기역학적 힘의 구성 요소

공기역학적 힘을 계산하는 식은 다음과 같습니다.

\mathbf {F} _{A}=\int _{\Sigma}(-\Delta p\mathbf {n} +\mathbf {f} )\,d\colons

위치:

\Delta p\equiv

Δ

\Delta p\equiv

≡

\\

deltap p\equiv }

정압과 자유 전류 압력의 차이

\Delta p\equiv

\mathbf {n} \equiv

n

◦

영역 요소의 외부 정규 벡터를

표시

합니다({\displaystyle

\mathbf {n

\

equiv

\mathbf {f} \equiv

◦

신체의 공기에 의해 실행되는

{\displaystyle \mathbf

{f} \

equiv}

접선

\mathbf {f} \equiv

응력 벡터

≡

{\

displaystyle \Sigma \equiv}

적절한

\Sigma \equiv

기준 표면

풍력 축에 투영하면 다음을 얻을 수 있습니다.

\mathbf {F} _{A}=-(\mathbf {i} _{w}D+\mathbf {j} _{w}Q+\mathbf {k} _{w}L)

위치:

≡

{\

displaystyle

D

\equiv}

드래그

D\equiv

Q\equiv

≡

{\

displaystyle

Q

\equiv}

횡력

Q\equiv

◦

(

디스플레이 스타일

L

\equiv)

리프트

L\equiv

공기역학 계수

자유 $\equiv q={\tfrac {1}{2}}\,\rho \,V^{2}$ 의 동적 압력 $\equiv q={\tfrac {1}{2}}\,\rho \,V^{2}$ ≡ $=$ 12 $\equiv q={\tfrac {1}{2}}\,\rho \,V^{2}$ $\equiv q={\tfrac {1}{2}}\,\rho \,V^{2}$ {\ $displaystyle \equiv$ q={\ $tfrac {1}{2}}\,\rho$ \, $V^{2}}$

적절한 기준면(평면의 경우 날개면) $\equiv S$ {\ $displaystyle \equiv$ S $}$

압력 계수 $\equiv C_{p}=displaydfrac {p-p_{\infty }{q}}$

마찰계수 $\equiv C_{f}=displaydfrac {f}{q}}$

드래그 계수 $\equiv C_{d}={dfrac{D}{qS}}=-{\dfrac{1}{S}}\int_{\Sigma}[(-C_{p})\mathbf{n} \mathbf{i_{w}} +C_{f}\mathbf{t} \mathbf} \mathbf{i_{w},\d\d\d$

횡력 계수 $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ S $=$ - $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ [ $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ ( $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ - $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ ) n $∙$ $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ + $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ ∙ $\equiv C_{Q}={\dfrac {Q}{qS}}=-{\dfrac {1}{S}}\int _{\Sigma }[(-C_{p})\mathbf {n} \bullet \mathbf {j_{w}} +C_{f}\mathbf {t} \bullet \mathbf {j_{w}} ]\,d\sigma$ w ] $σ$ \ \ \ \ \ $dfrac {1}$ { $S}}$ = - { \ $dfrac$ { $1}$ {S $}$ $\int$ _ ${\Sigma}$ \ mathbf} \ $t \$ n \ mathbf $}$ \ $mathbf$

리프트 계수 $\equiv C_{L}={dfrac{L}{qS}}=-{\dfrac{1}{S}}\int_{\Sigma}[(-C_{p})\mathbf{n} \mathbf{k_{w}} +C_{f}\mathbf{t} \d\dfac{\df$

고려된 표면의 모든 점에서 C와_f C를 알아야_p 합니다.

무차원 매개변수 및 공기역학적 체계

열 효과가 없는 경우 다음과 같은 세 가지 주목할 만한 무차원 수가 있습니다.

흐름의 압축성:

마하수

\equiv M=syslogdfrac {V}{a}}

흐름의 점도:

레이놀즈 수

\equiv Re=hovdfrac{\rho Vl}{\mu}}

흐름의 희박화:

크누드센 수

\equiv Kn=displaydfrac{l}}

위치:

a={\sqrt {kR\theta }}\equiv

a={\sqrt {kR\theta }}\equiv

a={\sqrt {kR\theta }}\equiv

a={\sqrt {kR\theta }}\equiv

≡

\ \

displaystyle

a = {\

sqrt {kR\theta

}\

equiv}

음속

a={\sqrt {kR\theta }}\equiv

displaystyle k\equiv}

비열비

R\equiv

일치에

의한

R

≡

\ disdisplaystyle

R\equiv

R

\equiv

◦ ∙

\theta \equiv

온도

\theta \equiv

표시

방식

디스플레이 스타일 \displaystyle = displaydfrac {mu}{\rho}{\sqrt {\dfrac {pi}{2R\theta }}=sqdfrac {M}{Re}}{\sqrt{\dfrac {k\pi}{2}}\equiv}

평균 자유 경로

λ에 따르면 세 가지의 가능한 희소성 등급이 있으며 그에 상응하는 운동을 다음과 같이 부릅니다.

연속체 전류(무시한 희소성): ${displaystyle {\dfrac {M}{Re}}\ll$
전환 전류(중간 수준의 희소성): ${displaystyle {\dfrac {M}{Re}}\approx$
자유 분자 전류(고희소화): ${displaystyle {\dfrac {M}{Re}}\gg1}$

흐름을 통과하는 물체의 움직임은 비행 역학에서 연속체 전류로 간주됩니다.신체를 둘러싸고 있는 공간의 외부 층에서 점도는 무시할 수 있습니다.그러나 경계층 근처의 흐름을 분석할 때는 점도 효과를 고려해야 합니다.

흐름의 압축성에 따라 다양한 종류의 전류를 고려할 수 있습니다.

비압축성 아음속 전류: $0<M<0.3$ < $0<M<0.3$ < $0<M<0.3$ ${displaystyle$ 0 < $M$ < $0.3}$
압축 가능한 아음속 전류: $0.3<M<0.8$ $0.3<M<0.8$ < $0.3<M<0.8$ $\$ $디스플레이 스타일$ 0 $.3$ $<M<0.8}$
천음속 전류: $.$ < $0.8<M<1.2$ {\ $displaystyle 0.8$ < M < 1 $.$ 2}
초음속 전류: $1.2<M<5$ $1.2<M<5$ < $1.2<M<5$ \ $display style$ 1 $.2$ $<M<5}$
극초음속 전류: $5<M$ < $5<M$ { $displaystyle$ 5 < $M$ }

드래그 계수 방정식 및 공기역학적 효율

차체의 기하학적 구조가 고정되어 있고 대칭 비행(β=0 및 Q=0)의 경우 압력 및 마찰 계수는 다음에 따라 함수가 됩니다.

C_{p}=C_{p}(\alpha,M,Re,P)

C_{f}=C_{f}(\alpha,M,Re,P)

위치:

{\displaystyle \alpha \equiv} 표시

공격각

P\equiv

표면의

P\equiv

점으로 고려된 P ≡

{\displaystyle

P\

}

이러한 조건에서 드래그 및 리프트 계수는 전적으로 차체의 공격 각도와 마하 및 레이놀즈 수에 따라 달라지는 함수입니다.공기역학적 효율은 양력과 항력 계수 사이의 관계로 정의되며 이러한 매개변수에도 의존합니다.

표시({stylebegin{cases}C_{D}=C_{D}(\alpha,M,Re)=C_{L}(\alpha,M,Re)={C_{L}}{C_{D}}\end{})

리프트 계수에 대한 드래그 계수의 의존성을 얻을 수도 있습니다.이 관계를 드래그 계수 방정식이라고 합니다.

C_{D}=C_{D}(C_{L},M,Re)\equiv

=

C_{D}=C_{D}(C_{L},M,Re)\equiv

C_{D}=C_{D}(C_{L},M,Re)\equiv

C_{D}=C_{D}(C_{L},M,Re)\equiv

)

≡

{\

displaystyle

C_

{D

}=

C_{D}(C_{L}, M, Re)\equiv}

드래그

C_{D}=C_{D}(C_{L},M,Re)\equiv

계수 방정식

공기역학적 효율은 좌표 원점의 탄젠트 선이 드래그 계수 방정식 그림에 닿는 C에 대해_L 최대값 E를_max 갖습니다.

항력 계수 C는_D 두 가지 방법으로 분해할 수 있습니다.첫 번째 전형적인 분해는 압력과 마찰 효과를 분리합니다.

C_{Df}=C_{Dp}{\begin{cases}C_{Df}={dfrac{D}{qS}=-{\dfrac{1}{S}\int_{f}\mathbf{i_{w}}\d\mathBf{C_{\Dp}}\d\caps}{FAC={\dfacs}{dfac{d}{d}{dfacs}{facs}{\d}\d}{d}\d

드래그 계수 방정식의 정의를 고려한 두 번째 전형적인 분해가 있습니다.이 분해는 방정식에서 리프트 계수의 효과를 분리하여 두 항 C와_D0_Di C를 얻습니다.C는_D0 기생 항력 계수로 알려져 있으며 제로 리프트 시 기본 항력 계수입니다.C는_Di 유도 항력 계수로 알려져 있으며 차체 리프트에 의해 생성됩니다.

C_{D}=C_{D0}+C_{Di}{\begin{cases}C_{D0}=(C_{D})_{C_{L}=0}\\C_{Di}\end{cases}}

포물선 및 일반 항력 계수

유도 항력 계수에 대한 좋은 시도는 리프트의 포물선 의존성을 가정하는 것입니다.

C_{Di}=kC_{L}^{2}\오른쪽 화살표 C_{D}=C_{D0}+kC_{L}^{2}

이제 공기역학적 효율은 다음과 같이 계산됩니다.

E=dirdfrac {C_{L}}{C_{D0}+kC_{L}^{2}}\오른쪽 화살표({begin{cases})E_{max}={2\dfrac{1}{2\dfrac{kC_{D0}}}}\(C_{L}})_{Emax}}={dfrac{C_{D0}}}\(C_{Di})_{Emax}=C_{D0}\end{cases}}}}

평면의 구성이 XY 평면에 대해 대칭이면 최소 항력 계수는 평면의 기생 항력과 같습니다.

C_{Dmin}=(C_{D})_{CL=0}=C_{D0}

그러나 구성이 XY 평면에 대해 비대칭인 경우 최소 드래그는 기생 드래그와 다릅니다.이러한 경우 최소 항력 값을 0 리프트 값으로 유지하면서 새로운 근사 포물선 항력 방정식을 추적할 수 있습니다.

C_{Dmin}=C_{DM}\neq(C_{D})_{CL=0}

C_{D}=C_{DM}+k(C_{L}-C_{LM}}^{2}

마하 수치에 따른 파라미터의 변동

압력 계수는 ^[4]마하 수치에 따라 아래에 제시된 관계에 따라 달라집니다.

C_{p}=displayfrac {C_{p0}}{\sqrt {1-{M_{\infty }}^{2}}}}

어디에

C는_p 압축 가능한 압력 계수입니다.
C는_p0 비압축 압력 계수입니다.
M은_∞ 자유 스트림 마하 수치입니다.

이 관계는 0.3 < M < 0.7에 대해 상당히 정확하며, M = 1일 때는 불가능한 물리적 상황인 π가 되며, 이를 프랜드틀-글라우어트 특이점이라고 합니다.

지정된 대기에서의 공기역학적 힘

공기역학적 힘 참조

안정성.

안정성은 항공기가 비행 경로의 방해에 대응할 수 있는 능력을 의미합니다.

데이비드 P에 따르면. 데이비스, 항공기 안정성에는 속도 안정성, 스틱 프리 정적 세로 안정성, 정적 가로 안정성, 방향 안정성, 진동 안정성, 나선 ^[5]^{: 164}안정성의 6가지 유형이 있습니다.

속도 안정성

순항 비행 중인 항공기는 일반적으로 속도가 안정적입니다.속도가 증가하면 드래그가 증가하여 구성 및 추력 설정을 위해 속도가 평형 상태로 돌아갑니다.속도가 감소하면 항력이 감소하고 항공기는 추력이 항력과 동일한 평형 속도로 다시 가속됩니다.

그러나 느린 비행에서는 리프트로 인한 항력으로 인해 속도가 감소함에 따라 항력이 증가합니다(또는 그 반대도 마찬가지입니다)이를 "끌기 곡선의 뒷면"이라고 합니다.속도가 감소하면 속도가 더 감소하기 때문에 항공기는 속도가 불안정해질 것입니다.

정적 안정성 및 제어

종방향 정적 안정성

세로 방향 안정성은 피치에서 항공기의 안정성을 의미합니다.안정적인 항공기의 경우, 항공기가 상승하면 날개와 꼬리가 하강 모멘트를 만들어 항공기를 원래 자세로 되돌리는 경향이 있습니다.불안정한 항공기의 경우, 피치의 교란은 투구 모멘트 증가로 이어질 것입니다.세로 방향 정적 안정성은 항공기가 초기 교란으로부터 복구할 수 있는 능력입니다.종방향 동적 안정성은 이러한 안정화 모멘트의 감쇠를 의미하며, 이는 피치의 지속적인 또는 증가하는 진동을 방지합니다.

방향 안정성

방향 또는 풍향계 안정성은 z축에 대한 비행기의 정적 안정성과 관련이 있습니다.세로 방향 안정성의 경우와 마찬가지로 항공기가 어떤 형태로든 요잉 교란을 받을 때 평형 상태로 되돌아가는 경향이 있어야 합니다.이 경우 요잉 모멘트 곡선의 기울기가 양수여야 합니다.이 안정성 모드를 가진 비행기는 항상 상대적인 바람을 향하기 때문에 풍향계 안정성이라는 이름이 붙습니다.

동적 안정성 및 제어

종방향 모드

종방향 운동을 설명하기 위해 4차 특성 방정식을 도출한 다음 이를 대략 고주파수 모드와 저주파 모드로 분해하는 것이 일반적입니다.여기서 채택된 접근법은 항공기 행동에 대한 질적 지식을 사용하여 처음부터 방정식을 단순화하고 보다 접근 가능한 경로로 결과에 도달하는 것입니다.

두 가지 종방향 운동(모드)을 단기 피치 진동(SPPO) 및 푸고이드라고 합니다.

단주기 피치 진동

(일반적으로 표준 구성 고정익 항공기의 엘리베이터를 통한) 피치의 짧은 입력(제어 시스템 용어로 임펄스)은 일반적으로 다듬어진 상태에 대한 오버슈팅으로 이어질 수 있습니다.이 전환은 새 트림을 중심으로 감쇠된 단순 고조파 모션을 사용하는 것이 특징은 다음과 같습니다.진동이 감쇠하는 데 걸리는 시간 동안 궤적의 변화는 거의 없습니다.

일반적으로 이 진동은 고주파(따라서 짧은 주기)이며 몇 초 동안 감쇠됩니다.실제 예로는 조종사가 새로운 상승 자세를 선택하는 것이 포함됩니다(예: 원래 자세에서 5° 상승).컨트롤 칼럼을 짧고 날카롭게 뒤로 당기면 일반적으로 새 트림 상태에 대한 진동이 발생합니다.진동이 제대로 감쇠되지 않으면 항공기가 새로운 조건에 안착하는 데 오랜 시간이 소요되어 조종사에 의한 진동이 발생할 수 있습니다.단기 모드가 불안정한 경우, 일반적으로 조종사가 일정 기간 동안 항공기를 안전하게 제어하는 것은 불가능합니다.

이 감쇠 조화 운동은 단기 피치 진동이라고 불립니다; 그것은 안정적인 항공기가 일반적인 비행 방향을 가리키는 경향에서 발생합니다.그것은 미사일 또는 로켓 구성의 풍향계 모드와 본질적으로 매우 유사합니다.운동은 주로 피치 자세 $\theta$ ({ $displaystyle \theta}($ 세타)와 $\alpha$ α({ $displaystyle \alpha})$ 를 포함합니다.관성축에 대한 속도 벡터의 방향은 $\theta -\alpha$ π - ${\displaystyle \theta -\alpha$ $\theta -\alpha$ 입니다. 속도 벡터는 다음과 같습니다.

u_{f}=U\cos(\theta -\alpha )

w_{f}=U\sin(\theta -\alpha )

$u_{f}$ 서 $u_{f}$ {{ $displaystyle u_{f$ ${$ 는 $w_{f}$ 속도의 관성 축 성분입니다.뉴턴의 제2법칙에 따르면 가속도는 힘에 비례하므로 관성축의 힘은 다음과 같습니다.

\"표시 스타일 X_{f}=m{\frac {du_{f}{dt}}=m440frac {dU}{dt}\cos(\theta -\alpha )-mU{\frac {dt(\theta -\alpha )}\sin(\theta -\alpha )}

\"표시 스타일 Z_{f}=m{\frac{f}{dt}}=mdwfrac{dU}{dt}}\sin(\theta -\alpha )+mU{\frac{d(\theta -\alpha )}\cos(\theta -\alpha )}

여기서 m은 질량입니다.움직임의 특성상 진동 $m{\frac {dU}{dt}}$ $m{\frac {dU}{dt}}$ 속도 $m{\frac {dU}{dt}}$ md ${\$ m ${\frac {dt}}$ 는 $m{\frac {dU}{dt}}$ 무시할 수 있으므로 다음과 같습니다.

X_{f}=-mU{\frac {d(\theta -\alpha )}{dt}}\sin(\theta -\alpha )

Z_{f}=mU{\frac {d(\theta -\alpha )}{dt}}\cos(\theta -\alpha )

하지만 그 힘은 신체의 압력 분포에 의해 생성되고, 속도 벡터라고 불립니다.그러나 설정된 속도(바람) 축은 관성 프레임이 아니므로 고정 축의 힘을 바람 축으로 분해해야 합니다.또한 z축을 따르는 힘에만 관심이 있습니다.

Z=-Z_{f}\cos(\theta -\alpha)+X_{f}\sin(\theta -\alpha )

또는:

Z=-mU{\frac {d(\theta -\alpha )}{dt}}

즉, 바람 축의 힘은 구심 가속도와 같습니다.

모멘트 방정식은 각운동량의 시간 미분입니다.

{\displaystyle M=B{\frac {d^{2}\theta}{dt^{2}}}} 표시

여기서 M은 피칭 모멘트이고, B는 피칭 축에 대한 관성 모멘트입니다. ${\frac {d\theta }{dt}}=q$ : ${\frac {d\theta }{dt}}=q$ $=$ q {\ $displaystyle {frac {d\$ theta}{dt $}=q$ 피치 속도.따라서 바람 축을 기준으로 한 모든 힘과 모멘트의 운동 방정식은 다음과 같습니다.

display{style{frac{d\alpha}{dt}=q+{\frac{Z}{mU}}}

display{style{frac{dq}{dt}=tvfrac{M}{B}}}

우리는 $\alpha$ α{{ $displaystyle \alpha}$ 및 $\alpha$ q $\alpha$ 의 동요와 그들의 시간 미분으로 인한 힘과 순간의 동요에만 관심이 있습니다.이들은 비행 조건에서 결정되는 안정성 파생물로 특징지어집니다.가능한 안정성 파생 모델은 다음과 같습니다.

{

입사로

Z_{\alpha }

인한 상승, 이것은 z축이 아래로 향하고 양의 입사로 인해 상승력이 발생하기 때문에 음의

Z_{\alpha }

입니다.

Z_{q}

{\

displaystyle

Z_{

q

Z_{q}

}} 피치 속도로 인한 리프트는 테일 발생률의 증가에서 발생하므로

Z_{\alpha }

에 비해 음의 값이지만 작습니다.

Mα{\alpha }

입사로

M_{\alpha }

인한 피칭 모멘트 - 정적 안정성 항.정적 안정성을 유지하려면 이 값이 음수여야 합니다.

M_{q}

{

displaystyle M_{q}}

피치

M_{q}

레이트로 인한 피칭 모멘트 - 피치 댐핑 용어, 이것은 항상

M_{q}

입니다.

테일은 날개의 유동장에서 작동하기 때문에 날개 입사 변화는 다운워시의 변화를 유발하지만, 날개 유동장 변화가 테일 리프트에 영향을 미치는 데에는 지연이 있으며, 이는 발생률에 비례하는 모멘트로 표시됩니다.

{\dot alpha} 표시 스타일

지연된 다운워시 효과는 꼬리를 더 많이 들어올리고 노즈 다운 모멘트를 $M_{\dot {\alpha }}$ 하므로 $M_{\dot {\alpha }}$ $˙$ {\alpha $}$ 이 $M_{{\dot \alpha }}$ (가) 음수일 것으로 예상됩니다.

작은 섭동력과 모멘트를 갖는 운동 방정식은 다음과 같습니다.

display{style{frac{d\alpha}{dt}=\left(1+{\frac{Z_{q}}{mU}}\right)q+{\frac {Z_{\alpha }}{mU}\alpha }

표시({style {\frac {dq}{dt}}=nbfrac {M_{q}}{B}}q+{\frac {M_{\alpha }}{B}\alpha +{\frac {M_{\dot {\alpha }}{B}}{\dot {\alpha}}}}}}

이것들은 $\alpha$ α{ $displaystyle \alpha$ 에서 2차 선형 미분 방정식으로 생성되도록 조작될 수 있습니다.

표시({\frac {d^{2}\alpha }{dt^{2}})-\left({\frac {Z_{\alpha }}{m)U}}+{\frac {M_{q}}{B}}+(1+{\frac {Z_{q}}}{mU}){\frac{M_{\dot{alpha}}{B}}\right){\frac{d\alpha}{dt}}+\left({\frac{Z_{\alpha}}}}{mU}}{\frac {M_{q}}{B}}-{\frac {M_{\alpha }}{B}}(1+{\frac {Z_{q}}{mU})\오른쪽)\알파 =0}

이는 감쇠된 단순 고조파 운동을 나타냅니다.

${$ 를 ${\frac {Z_{q}}{mU}}$ 야 합니다. $U}}$ 은 ${\frac {Z_{q}}{mU}}$ (는) 단일에 비해 작으므로 M $M_{\alpha }<{\frac {Z_{\alpha }}{mU}}M_{q}$ < $M_{\alpha }<{\frac {Z_{\alpha }}{mU}}M_{q}$ $M_{\alpha }<{\frac {Z_{\alpha }}{mU}}M_{q}$ $M_{\alpha }<{\frac {Z_{\alpha }}{mU}}M_{q}$ U $q$ {\alpha $}<{\frac$ { $Z_$ {\alpha $}{m이면$ $α$ \ $displaystyle$ \alpha $\alpha$ }('강성' 용어)의 계수는 양수입니다. $U}M_{q$ 이 표현식은 항공기의 종방향 정적 안정성을 $M_{\alpha }$ 정의하는 $Mα$ {{\ $alpha$ $M_{\alpha }$ 에 $M_{\alpha }$ 지배되며 안정성을 위해 음수여야 합니다.댐핑 항은 다운워시 효과에 의해 감소하며, 빠른 자연 반응과 무거운 댐핑을 모두 갖춘 항공기를 설계하는 것은 어렵습니다.일반적으로 반응은 충분히 감쇠되지 않지만 안정적입니다.

푸고이드

스틱이 고정된 상태로 유지되면 항공기는 직선 및 수평 비행을 유지하지 않고(현재 고도 및 추력 설정에서 수평 비행을 위해 완벽하게 다듬어진 경우를 제외하고) 잠수, 수평 이탈 및 상승을 시작합니다.조종사가 개입할 때까지 이 사이클을 반복합니다.이처럼 속도와 높이가 긴 주기로 진동하는 것을 푸고이드 모드라고 합니다.이는 SSPO가 적절한 기능을 수행하고 공격 각도를 공칭값 근처로 유지한다고 가정하여 분석됩니다.주로 영향을 받는 두 가지 상태는 비행 경로 각도 $\gamma$ ({ $displaystyle \gamma}($ 감마)와 속도입니다.운동의 작은 섭동 방정식은 다음과 같습니다.

{\dt}{displaystyle mU{\frac}{dt}=-Z}

즉 구심력이 양력의 섭동과 같다는 것입니다.

속도의 경우 궤적을 따라 해결:

m{\frac {du}{dt}=X-mg\gamma

여기서 g는 지구 표면에서의 중력에 의한 가속도입니다.궤적을 따르는 가속도는 순 x 방향 힘에서 무게 성분을 뺀 것과 같습니다.비행 경로 각도에 따라 상당한 공기역학적 도함수가 달라질 것으로 예상해서는 안 되므로 $({$ 와 $X_{u}$ $({$ 만 $Z_{u}$ $X_{u}$ 하면 됩니다. ${$ 는 $X_{u}$ 속도가 증가할수록 드래그 증분입니다. 이는 음의 값입니다. ${$ 와 $Z_{u}$ 마찬가지로 속도 증가로 인한 리프트 증분입니다. 리프트는 z축과 반대의 의미로 작용하기 때문에 음의 값이기도 합니다.

운동 방정식은 다음과 같습니다.

{{dt}}=-Z_{u}u}를(를) 표시 스타일 mU{\frac{d\frac{dt}

m{\frac {du}{dt}=X_{u}u-mg\gamma

이것들은 비행 경로 각도 또는 속도 섭동에서 2차 방정식으로 표현될 수 있습니다.

표시({style\frac {d^{2}}-{\frac {X_{u}}{m}}{\frac {du}}-{\frac {Z_{u}g}{mU}u=0}

이제 리프트는 무게와 거의 같습니다.

Z=novfrac{1}{2}}\rho U^{2}c_{L}S_{w}=W

$\rho$ 서 $ρ$ 는 공기 $\rho$ 밀도이고 $,$ $S_{w}$ {{ $displaystyle S_{w}$ 는 $S_{w}$ 날개 면적이고 $,$ $c_{L}$ { $displaystyle c_{L}$ 은 $c_{L}$ $c_{L}$ 계수(발생이 일정하기 때문에 일정하다고 가정함)입니다. 대략 다음과 같습니다.

Z_{u}=twfrac {2}W}{U}}=nbfrac{2mg}{U}}

푸고이드의 주기 T는 u의 계수에서 구합니다.

display{style{frac{2\pi}{T}=sksqrt{frac{2g^{2}}{U^{2}}}}

또는:

T=displayfrac {2\pi U}{{\sqrt {2}}}

리프트가 드래그보다 훨씬 크기 때문에 푸고이드는 기껏해야 약간 축축해집니다.속도가 고정된 프로펠러가 도움이 될 것입니다.피치 회전의 심한 감쇠 또는 큰 회전 관성은 짧은 주기 모드와 푸고이드 모드 사이의 결합을 증가시켜 푸고이드를 수정합니다.

가로 모드

Antonov An-225는 안정성이 떨어지지만 기동성이 더 뛰어납니다.

대칭 로켓 또는 비산물의 경우, 요의 방향 안정성은 피치 안정성과 동일하며, 짧은 주기 피치 진동과 유사하며, 요 평면은 피치 평면 안정성 파생물과 동일합니다.이러한 이유로, 피치 및 요 방향 안정성은 총칭하여 미사일의 "웨더콕" 안정성으로 알려져 있습니다.

항공기는 피치와 요 사이의 대칭성이 부족하기 때문에 요의 방향 안정성은 다른 안정성 도함수 집합에서 도출됩니다.요 평면 방향 안정성을 설명하는 짧은 주기 피치 진동에 해당하는 요 평면을 더치 롤이라고 합니다.피치 평면 모션과 달리 횡방향 모드는 롤링 및 요 모션을 모두 포함합니다.

더치롤

일반적으로 운동 방정식은 공식적인 조작을 통해 도출되며, 이는 엔지니어에게 수학적인 손놀림에 해당합니다.현재 접근 방식은 피치 평면 분석을 따라 합리적으로 익숙한 개념의 관점에서 방정식을 공식화합니다.

방향타 페달을 통해 임펄스를 적용하면 롤과 요의 진동인 네덜란드 롤을 유도해야 하며, 롤 모션은 요를 4분의 1 주기로 지연시켜 날개 끝이 항공기에 대한 타원 경로를 따르도록 해야 합니다.

요 평면 변환 방정식은 피치 평면에서와 같이 구심 가속도와 측면 힘을 동일시합니다.

display{style{frac {d\dt}}=tftfrac {Y}{mU}-r}

$\beta$ 서 $\beta$ β{\ $displaystyle \beta}($ 베타)는 측면 미끄러짐 각도, Y 측면 힘 및 r 요 레이트입니다.

모멘트 방정식은 좀 더 까다롭습니다.트림 조건은 공기 흐름에 대한 공격 각도에서 항공기에 적용됩니다.본체 x축이 바람 축의 기준 방향인 속도 벡터와 맞지 않습니다.즉, 바람 축은 주축이 아닙니다(질량이 요 및 롤 축에 대해 대칭적으로 분포되지 않음).Y축 방향, 즉 종이의 평면 안으로 위치 -z, x의 질량 요소의 움직임을 고려합니다.

롤 속도가 p이면 입자의 속도는 다음과 같습니다.

{\displaystyle v=-pz+xr} 표시

두 개의 항으로 구성된 이 입자에 가해지는 힘은 첫 번째는 v 변화 속도에 비례하고 두 번째는 물체가 움직일 때 속도 성분의 방향이 바뀌기 때문입니다.후자의 용어는 나중에 폐기되는 소량(pq, pr, qr)의 교차 제품을 생성합니다.이 분석에서는 명확성을 위해 처음부터 폐기됩니다.실제로, 우리는 동시 롤 및 요 레이트로 인한 입자 속도의 방향이 운동 전반에 걸쳐 크게 변하지 않는다고 가정합니다.이 단순화된 가정에서 입자의 가속도는 다음과 같습니다.

표시{style{frac{dv}}=-{\frac{dp}{dt}z+{\frac{dr}{dt}x}

요잉 모멘트는 다음과 같습니다.

\dx480frac {dv}}=-{\frac {dp}{dt}xz\frac m+{\frac {dr}{dt}x^{2}\frac m

y 방향의 입자 오프셋으로 인해 추가적인 요잉 모멘트가 ${\frac {dr}{dt}}y^{2}\delta m$ . ${\frac {dr}{dt}}y^{2}\delta m$ ${\frac {dr}{dt}}y^{2}\delta m$ 2 ${{{frac {dr}}y^{2}\drd$ ty 2 µm

요잉 모멘트는 차체의 모든 입자에 대한 합으로 구할 수 있습니다.

{\frac{dp}{dt}}\int xzdm+{\frac{dr}}\int x^{2}+y^{2}dm=-E{\frac{dp}}+C{\frac{dr}{dt}}}}

여기서 N은 요잉 모멘트, E는 관성의 곱, C는 요 축 주위의 관성 모멘트입니다.유사한 추론이 롤 방정식을 산출합니다.

{\frac {dp}{dt}-E{\frac {dr}{dt}}표시 스타일 L=A}

여기서 L은 롤링 모멘트이고 A는 관성 롤 모멘트입니다.

횡방향 및 종방향 안정성 도함수

상태는 $\beta$ β{\ $displaystyle \beta}($ 측면 미끄러짐), r(요 레이트) 및 p(측면 미끄러짐)이며 모멘트는 N(요) 및 L(롤), 힘은 Y(측면)입니다.이 모션과 관련된 9개의 안정성 파생 모델이 있으며, 다음은 이러한 파생 모델이 어떻게 발생하는지 설명합니다.그러나 더 나은 직관적인 이해는 모형 비행기를 가지고 노는 것과 각 구성 요소의 힘이 사이드 슬립과 각 속도의 변화에 의해 어떻게 영향을 받는지를 고려하는 것으로 얻을 수 있습니다.

{\

디스플레이

Y_{\beta }

스타일

Y_

{\

beta} 측면 미끄러짐으로 인한 측면 힘(요우가 없는 경우).

사이드슬립은 지느러미와 동체로부터 부력을 발생시킵니다.또한, 날개가 이면체를 갖는 경우, 양의 롤 각도에서의 사이드 슬립은 우현 날개의 입사를 증가시키고 좌현 측면에서의 사이드 슬립을 감소시켜, 사이드 슬립 방향과 정반대의 순력 성분이 발생하게 됩니다.날개 뒤로 쓸어주는 것은 입사에 동일한 영향을 미치지만, 날개가 수직면에서 기울어지지 않기 때문에 뒤로 쓸어주는 것만으로는 $Y_{\beta }$ {\ $displaystyle$ Y_{\ $beta$ 에 영향을 주지 않습니다. 그러나 사이드 슬립의 날개 입사 효과를 상쇄하기 위해 고성능 항공기에서 뒤로 쓸어주는 각도가 높은 다면체를 사용할 수 있습니다.이상하게도 이것은 날개 구성이 $($ 의 경우와 비교하여 \displaystyle $Y_{\beta$ }) $Y_{\beta }$ 에 기여하는 신호를 되돌리지 않습니다.

{

롤

Y_{p}

속도로 인한 사이드 포스입니다.

롤 레이트는 핀에서 발생을 유발하며, 이에 상응하는 부력을 생성합니다.또한, 포지티브 롤(우현 날개 아래)은 우현 날개의 리프트를 증가시키고 좌현에서 리프트를 감소시킵니다.날개에 이면체가 있는 경우, 이는 결과적인 측면 미끄러짐 경향에 순간적으로 반대되는 측면 힘을 초래합니다.다면체 날개 및/또는 안정기 구성은 핀 효과가 스웜프된 경우 측면 힘의 부호가 반전되도록 할 수 있습니다.

Y_{r}

{{

displaystyle Y_{r}

요

Y_{r}

레이트로 인한 측면 힘.

요잉은 방향타, 핀 및 동체의 입사로 인한 측면력을 발생시킵니다.

{

사이드

N_{\beta }

슬립 힘으로 인한 요잉 모멘트.

방향타 입력이 없는 상태에서 측면 미끄러짐으로 인해 동체와 엠펜에 입사가 발생하므로 수평 비행 조건에서 항공기의 기수를 다시 바람 쪽으로 향하게 하는 방향 강성으로만 대응하는 요잉 모멘트가 생성됩니다.주어진 롤 $N_{\beta }$ $N_{\beta }$ β({\ $displaystyle N_{\beta})$ 에서 $N_{\beta }$ 사이드 슬립 조건에서는 방향타 입력이 없어도 코가 사이드 슬립 방향으로 향하는 경향이 있어 아래로 나선형 비행이 발생합니다.

{

롤

N_{p}

속도로 인한 요잉 모멘트입니다.

롤 레이트는 핀 리프트를 생성하여 요잉 모멘트를 발생시키고 또한 날개의 리프트를 차등적으로 변경하여 각 날개의 유도 드래그 기여도에 영향을 주어 (작은) 요잉 모멘트 기여를 유발합니다.양의 롤은 일반적으로 엠펜니지가 다면체이거나 핀이 롤 축 아래에 있지 않는 한 $N_{p}$ 의 $({$ 값을 발생시킵니다.날개 축이 일반적으로 무게 중심과 밀접하게 정렬되어 있기 때문에 이면체 또는 이면체 날개 리프트 차이로 인한 횡력 구성요소는 $({$ N_ ${p})$ 에 $N_{p}$ $N_{p}$ 영향을 미치지 않습니다.

N_{r}

{\

displaystyle

N_

{r}

요

N_{r}

레이트로 인한 요 모멘트입니다.

임의의 롤 각도에서 요 레이트 입력은 방향타, 핀 및 동체 힘 벡터를 생성하며, 이들은 결과적으로 요잉 모멘트를 지배합니다.또한 요잉은 선외기 윙의 속도를 높이는 동시에 선외기 윙의 속도를 높이며, 이에 상응하는 드래그 변화로 인해 (작은) 반대의 요 모멘트가 발생합니다. $({$ r $N_{r}$ })은 항공기의 코를 다시 바람 쪽으로 향하게 하는 고유한 방향 강성에 반대하며 항상 요 레이트 입력 부호와 일치합니다.

{

사이드

L_{\beta }

슬립으로 인한 롤링 모멘트.

양의 사이드 슬립 각도는 구성에 따라 양 또는 음의 롤 모멘트를 발생시킬 수 있는 엠펜니지 발생을 생성합니다.측면 미끄러짐 각도가 0이 아닌 경우 이면 날개와 마찬가지로 항공기를 수평으로 되돌리는 롤링 모멘트가 발생합니다.높은 스윕 날개의 경우 결과적인 롤링 모멘트는 모든 안정성 요구 사항에 대해 과도할 수 있으며, 날개 스위프 유도 롤링 모멘트의 효과를 상쇄하기 위해 사면체를 사용할 수 있습니다.

L_{r}

{{

displaystyle L_{r}}

요

L_{r}

레이트로 인한 롤링 모멘트입니다.

요는 선외기 윙의 속도를 높이는 동시에 선외기 윙의 속도를 줄여 선외기 측에 롤링 모멘트를 발생시킵니다.핀의 기여는 일반적으로 롤 축 위의 다면체 안정기(또는 롤 축 아래의 이면체)에 의해 상쇄되지 않는 한 내부 롤링 효과를 지원합니다.

L_{p}

{

displaystyle L_{p}

롤

L_{p}

속도로 인한 롤링 모멘트입니다.

Roll은 우현 및 좌현 날개 모두에 역회전력을 발생시키는 동시에 엠펜지에서도 역회전력을 발생시킵니다.이러한 상반된 롤링 모멘트 효과는 롤 속도를 유지하기 위해 에일러론 입력에 의해 극복되어야 합니다.롤이 0이 아닌 롤 각도에서 정지하는 경우 후속 사이드 슬립에 의해 유도된 $L_{\beta }$ β{\ $displaystyle$ L_ ${\beta}$ 상향 $L_{\beta }$ 롤링 모멘트는 $L_{\beta }$ 슬립 유도 요 레이트에 의해 유도된 $L_{r}$ L $L_{r}$ r {\ $displaystyle L_{r}$ 롤링 $L_{r}$ 모멘트가 차례로 초과되지 않는 한 항공기를 수평으로 되돌려야 합니다.종방향 안정성은 후자의 효과를 최소화함으로써 보장되거나 개선될 수 있습니다.

운동 방정식

더치 롤은 짧은 주기 피치 진동과 유사한 핸들링 모드이기 때문에 궤적에 미칠 수 있는 모든 영향은 무시될 수 있습니다.차체 측정기는 사이드 슬립 각도의 변화 속도와 회전 속도로 구성됩니다.네덜란드 롤을 연구하는 제한된 목적을 위해 궤적에 영향을 미치지 않는 경우 후자를 0으로 간주합니다.

display{style {d\frac}{dt}=-r}

요 및 롤 방정식과 안정성 도함수는 다음과 같습니다.

C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p

C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p

-

C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p

C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p

C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p

=

C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p

- N

C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p

C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p

t

C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p

+

C{\frac {dr}{dt}}-E{\frac {dp}{dt}}=N_{\beta }\beta -N_{r}{\frac {d\beta }{dt}}+N_{p}p

p

\ \ \

frac {dr}

{

dt}-E

{\

frac {dp}}= N_{\ beta

}\

n_

{r

}{\ frac {d\

dt

}}+ N_{p}(

)

=

L_{p}p}(

롤)

롤 가속도로 인한 관성 모멘트는 공기역학 용어에 비해 작기 때문에 방정식은 다음과 같습니다.

\displaystyle - C{\frac {d^{2}\colon }{dt^{2}}=N_{\beta}\colon -N_{r}{\frac {d\colon }{dt}}+N_{p}p}

{\frac {d^{2}\displaystyle E{\frac}{dt^{2}}=L_{\beta}\deta -L_{r}{\frac {d\frac }{displaystyleL_{p}p}

이는 롤 레이트 또는 사이드 슬립을 지배하는 2차 방정식이 됩니다.

{\frac{N_{p}}{C}}{\frac{E}{A}}-{\frac{L_{p}}{A}\right){\frac{d^{2}\beta}{dt^{2}}}+\left({\frac{L_{p}}}}{\frac{\frac{\frac{L_{p}}}}}}}{{\frac}}}A}{\frac {N_{r}}{C}}-{\frac {N_{p}}{C}}{\frac {L_{r}}{A}}{\right){\frac {d\beta}{dt}}-\left({\frac {L_{p}}}}{\frac {{\frac {L_p}}}}}{A}{\frac {N_{\beta }}{C}}-{\frac {L_{\beta }{A}}{\frac {N_{p}}{C}}\right)\beta =0}

롤 속도에 대한 방정식은 동일합니다.그러나 롤 각도인 $\phi$ {\ $displaystyle \phi}($ phi)는 다음과 같이 제공됩니다.

display{style{frac{d\phi}{dt}=p}

만약 p가 감쇠된 단순 고조파 운동이라면, $\phi$ \ $phi$ 도 마찬가지이지만, 롤은 롤 속도와 직교해야 하며, 따라서 사이드 슬립도 마찬가지입니다.이 모션은 롤 및 요의 진동으로 구성되며, 롤 모션은 요의 후방에서 90도 지연됩니다.날개 끝은 타원형 경로를 따라갑니다.

안정성을 위해서는 "강성" 및 "댐핑" 항이 양수여야 합니다.다음은 다음과 같습니다.

{\frac {{\frac {L_{p}}{A}}{\frac {N_{r}}{C}}-{\frac {N_{p}}{C}}{\frac {L_{r}}{A}}}{{\frac {N_{p}}{C}}{\frac {E}{A}}-{\frac {L_{p}}{A}}}}

A}{\frac {N_{r}}{C}}-{\frac {N_{p}}{C}}{\frac {L_{r}}{A}}{{\frac {E}{A}}-{\frac {L_{

A}}}}(

댐핑)

{\frac {{\frac {L_{\beta }}{A}}{\frac {N_{p}}{C}}-{\frac {L_{p}}{A}}{\frac {N_{\beta }}{C}}}{{\frac {N_{p}}{C}}{\frac {E}{A}}-{\frac {L_{p}}{A}}}}

A}{\frac{N_{\beta}}{C}}{{\frac{N_{p}}{C}}{\frac{E}{A}}-{\frac{L_{p}}{

A}}}}(

강성)

분모는 항상 음수인 롤 댐핑 $L_{p}$ 인 $L_{p}$ ({ $displaystyle$ L_ $L_{p}$ p $}})$ 에 $L_{p}$ 지배되므로 이 두 식의 분모는 양수입니다.

$-L_{p}N_{\beta }$ 강성" 조건을 $-L_{p}N_{\beta }$ 하면 Lp $-L_{p}N_{\beta }$ $({$ - $L_{p}N_{\beta})$ 는 $-L_{p}N_{\beta }$ 양수입니다. $({$ 는 $L_{p}$ 항상 음수이고 $N_{\beta }$ ({\ $displaystyle N_{\beta})$ 는 양수이기 $N_{\beta }$ $L_{p}$ 입니다. ${$ 는 $L_{\beta }$ 일반적으로 음수인 $N_{p}$ ${$ 는 $N_{p}$ $L_{\beta }$ 입니다.과도한 이면체는 네덜란드 롤을 불안정하게 만들 수 있으므로, 스위프 날개가 많이 있는 구성은 날개 스위프 기여도를 ${\$ 에 상쇄하기 위해 사면체가 필요합니다.

댐핑 용어는 롤 댐핑 및 요 댐핑 파생 모델의 곱에 의해 지배되며, 이들은 모두 음이므로 양의 값을 갖습니다.그러므로 더치 롤은 축축해야 합니다.

움직임은 무게 중심의 약간의 측면 움직임을 동반하며, 보다 "정확한" 분석은 ${\$ $Y_{\beta }$ 의 $Y_{\beta }$ 용어를 도입할 것입니다.안정성 도함수를 계산할 수 있는 정확성을 고려할 때, 이는 항공기 기하학과 취급 사이의 관계를 모호하게 만드는 역할을 하는 불필요한 교육입니다. 이는 이 기사의 기본 목적입니다.

롤 침하

스틱을 옆으로 돌려 중앙으로 돌리면 롤 방향이 순으로 변경됩니다.

롤링 모션은 자연적인 안정성이 결여된 것이 특징이며, 관성 롤링 각도에 반응하여 모멘트를 생성하는 안정성 파생 요소는 없습니다.롤 장애는 조종사 또는 자동 조종사의 개입에 의해서만 취소되는 롤 레이트를 유도합니다.이는 사이드 슬립 또는 요 레이트의 미미한 변화로 발생하므로 움직임의 방정식은 다음과 같이 감소합니다.

디스플레이 스타일 A{\frac {dp}{dt}}=L_{p}p.}

${$ 는 $L_{p}$ 음수이므로 롤 속도는 시간이 지남에 따라 $L_{p}$ 합니다.롤 레이트는 0으로 감소하지만 롤 각도를 직접 제어할 수는 없습니다.

스파이럴 모드

단순히 막대기를 가만히 유지하는 것만으로도, 수평에 가까운 날개에서 시작할 때, 항공기는 일반적으로 직선 비행 경로의 한쪽으로 점차 방향을 바꾸는 경향이 있습니다.(약간 불안정한) 나선형 ^{[citation needed]}모드입니다.

Spiral 모드 궤적

궤적을 연구할 때 관심이 있는 것은 물체의 방향이 아니라 속도 벡터의 방향입니다.수평으로 투영될 때 속도 벡터의 방향은 μ ${displaystyle \mu}($ mu)로 $\mu$ 되는 트랙이라고 합니다.신체 방향은 제목이라고 하며, $\psi$ {\ $displaystyle \psi}($ psi)로 표시됩니다.운동의 힘 방정식은 ^{[citation needed]}무게의 구성 요소를 포함합니다.

display{style{frac{d\mu}{dt}=tvfrac{Y}{mU}}+{\frac {g}{U}\phi }

여기서 g는 중력 가속도이고 U는 속도입니다.

안정성 파생 모델 포함:

display{style{frac {d\mu}{dt}=tvfrac {Y_{\beta}{mU}}\beta +{\frac {Y_{r}}{mU}}r+{\frac{Y_{p}}{mU}}p+{\frac {g}{U}\phi }

롤 속도와 요 속도는 작을 것으로 예상되므로 ${{$ $Y_{p}$ ${$ 의 $Y_{p}$ 기여는 무시됩니다.

사이드 슬립 및 롤 속도는 점진적으로 변화하므로 시간 파생 모델은 무시됩니다.요 및 롤 방정식은 다음과 같이 감소합니다.

N_{\beta }\beta +N_{r}{\frac {d\mu }{dt}}+N_{p}p=0

+

N_{\beta }\beta +N_{r}{\frac {d\mu }{dt}}+N_{p}p=0

N_{\beta }\beta +N_{r}{\frac {d\mu }{dt}}+N_{p}p=0

+

N_{\beta }\beta +N_{r}{\frac {d\mu }{dt}}+N_{p}p=0

=

N_{\

beta}\colon

+

N_{r}{\frac {d\mu}{dt}}+N_{p}p=0}(

)

L_{\beta }\beta +L_{r}{\frac {d\mu }{dt}}+L_{p}p=0

L_{p}p=0}(

롤)

β $\beta$ 및 $\beta$ p에 대한 $\beta$ :

\displaystyle = displayfrac {(L_{r}-L_{p}N_{{r}}}{(L_{p}N_{\beta}-N_{p}L_{\beta}}}}{\frac {d\mu}}

p=displayfrac {(L_{\beta}N_{r}-L_{r}N_{\beta}}{(L_{p}-N_{p}L_{\beta}}}}{\frac {d\mu}}}

힘 방정식에서 사이드 슬립과 롤 속도를 대입하면 롤 각도의 1차 방정식이 생성됩니다.

표시({style\frac {d\phi}{dt}}=mg{\frac {(L_{\beta})N_{r}-N_{\beta}}{mU(L_{p}N_{\beta})-N_{p}L_{\beta})-Y_{\beta}(L_{R_{P}}}}}}{P_{P_{P_{P_{P_{R_R_R_}}})

$\phi$ 는 $ϕ$ 의 계수가 $\phi$ 양의 $값$ 인지 음의 값인지에 따라 기하급수적으로 증가하는 것입니다 $.$ 분모는 일반적으로 음수이므로 $L_{\beta }N_{r}>N_{\beta }L_{r}$ $L_{\beta }N_{r}>N_{\beta }L_{r}$ > $L_{\beta }N_{r}>N_{\beta }L_{r}$ $({$ 이 $L_{\beta }N_{r}>N_{\beta }L_{r}$ 합니다. $N_{\beta }L_{r}}($ 두 제품 모두 양성입니다.이는 네덜란드 롤 안정성 요구사항과 직접적으로 상충되며, 네덜란드 롤과 스파이럴 모드가 본질적으로 ^{[citation needed]}모두 안정적인 항공기를 설계하는 것은 어렵습니다.

스파이럴 모드는 시간 상수가 길기 때문에 조종사가 개입하여 효과적으로 안정시킬 수 있지만, 더치 롤이 불안정한 항공기는 비행하기 어려울 것입니다.안정적인 네덜란드 롤 모드로 항공기를 설계하는 것이 일반적이지만 약간 불안정한 스파이럴 ^{[citation needed]}모드입니다.

참고 항목

레퍼런스

메모들

^ Flightwise Volume 2 - 항공기 안정성 및 제어, 크리스 카펜터 1997, Airlife Publishing Ltd., ISBN185310 8707, 그림 2.6
^ https://archive.org/details/DTIC_ADA124610 페이지V-5
^ ^a ^b ^c "MISB Standard 0601" (PDF). Motion Imagery Standards Board (MISB). Retrieved 1 May 2015. 파일 위치:MISB 표준 0601.pdf.
^ Anderson, John D. (2005). Introduction to flight (5. ed., internat. ed.). Boston [u.a.]: McGraw-Hill. pp. 274–275. ISBN 9780071238182.
^ Davies, David P. (1971). Handling the Big Jets: An Explanation of the Significant Differences in Flying Qualities Between Jet Transport Aeroplanes and Piston Engined Transport Aeroplanes, Together with Some Other Aspects of Jet Transport Handling (3rd ed.). Air Registration Board. ISBN 0903083019.

서지학

NK Sinha와 Nanthkrishnan(2013), 분기 및 지속 방법 소개를 통한 초등 비행 역학, CRC Press, Taylor & Francis.
Babister, A. W. (1980). Aircraft dynamic stability and response (1st ed.). Oxford: Pergamon Press. ISBN 978-0080247687.

외부 링크

[1] Flightwise Volume 2 - 항공기 안정성 및 제어, 크리스 카펜터 1997, Airlife Publishing Ltd., ISBN185310 8707, 그림 2.6

[2] ttps://archive.org/details/DTIC_ADA124610 페이지V-5

[MISB-3] "MISB Standard 0601" (PDF). Motion Imagery Standards Board (MISB). Retrieved 1 May 2015. 파일 위치:MISB 표준 0601.pdf.

[4] Anderson, John D. (2005). Introduction to flight (5. ed., internat. ed.). Boston [u.a.]: McGraw-Hill. pp. 274–275. ISBN 9780071238182.

[Davies-5] Davies, David P. (1971). Handling the Big Jets: An Explanation of the Significant Differences in Flying Qualities Between Jet Transport Aeroplanes and Piston Engined Transport Aeroplanes, Together with Some Other Aspects of Jet Transport Handling (3rd ed.). Air Registration Board. ISBN 0903083019.

[1]

[2]

[3]

[4]

[5]

Search