기술함수

제어시스템 이론에서, 1930년대에 니콜라이 미트로파노비치 크릴로프와 니콜라이 보골리우보프가 개발하고 ^[1][2]랄프 코첸버거가^[3] 확장한 기술함수(DF) 방법은 특정 비선형 제어 문제를 분석하기 위한 대략적인 절차다. 입력 파형의 진폭에 따라 달라지는 LTI(Linear-time-invariant) 전송 함수에 의해 조사 중인 비선형 시스템의 근사치인 준선형화에 기초한다. 정의상, 진정한 LTI 시스템의 전송 함수는 LTI 시스템이 선형이기 때문에 입력 함수의 진폭에 의존할 수 없다. 따라서 진폭에 대한 이러한 의존성은 비선형 시스템 동작의 두드러진 특징을 포착하기 위한 시도로 결합되는 선형 시스템 계열을 생성한다. 기술 함수는 비선형 시스템 설계에 광범위하게 적용되는 몇 안 되는 방법 중 하나이며, 산업 공정 제어, 서보마이즘 및 전자 오실레이터와 같은 폐쇄 루프 제어기의 한계 주기를 분석하기 위한 표준 수학 도구로 매우 널리 사용된다.

방법

느린 안정 선형 시스템과 함께 계단식(예: 포화 증폭기 또는 데드밴드 효과가 있는 요소)으로 이루어진 불연속(그러나 조각처럼 연속된) 비선형성에 대한 피드백을 고려한다. 비선형성에 피드백이 제시되는 연속 영역은 선형 시스템의 출력 진폭에 따라 달라진다. 선형 시스템의 출력 진폭이 감소함에 따라 비선형성은 다른 연속 영역으로 이동할 수 있다. 한 연속 영역에서 다른 연속 영역으로의 전환은 주기적인 진동을 발생시킬 수 있다. 기술 함수 방법은 느린 시스템이 단일 주파수를 중심으로 모든 에너지를 집중시키는 저역 통과 또는 대역 통과 필터와 같은 역할을 한다고 가정하여 그러한 진동(예: 기본 주파수)의 특성을 예측하려고 시도한다. 출력 파형에 여러 모드가 있더라도 이 방법은 주파수 및 가능한 진폭과 같은 속성에 대한 직관력을 제공할 수 있다. 이 경우 기술 함수 방법은 피드백 시스템의 슬라이딩 모드를 설명하는 것으로 생각할 수 있다.

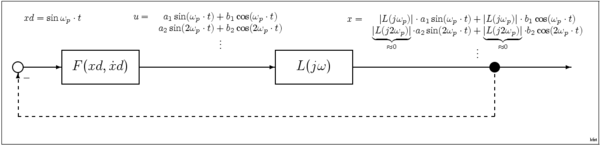
이 저역-통과 가정을 사용하여 시스템 응답은 사인 파형 제품군 중 하나로 설명될 수 있다. 이 경우 시스템은 진폭 A와 자주 발생하는 진폭 A의 사인파로 구성된 입력에 시스템 응답을$$ 제공하는 사인 입력 기술 함수(SIDF) $H{\displaystyle (A}$ , ${\displaystyle j}$ Ω${\displaystyle }$)$${\$displaysty H(A,\,j\$j\$omega )}$로 특징지어진다.y $\Omega {\displaystyle }$ ${\displaystyle \omega$ 이 SIDF는 선형 시스템의 특성화에 사용되는$$ 전송 함수 $($ ${\displaystyle \Omega }$ ) $displaystyle H(j\omega )}$의 수정이다. 준선형 시스템에서 입력이 사인파인 경우 출력은 동일한 주파수의 사인파가 되지만 $H{\displaystyle (A,}$ ${\displaystyle \Omega }$)에 의해 주어진 대로 스케일링된 진폭과 이동 위상이 있는 사인파가 될 것이다$.\}$ {\디스플레이 스타일 $H(A,\,j\$j\$omega )}.$ 사인파에 대한 응답이 순수한 사인파가 아님에도 불구하고 많은 시스템은 대략적으로 준선형이다. 출력에서 대부분의 에너지는 실제로 입력과$$ 동일한 주파수 $\Omega {\displaystyle }$ ${\displaystyle \omega }$에 있다. 이는 그러한 시스템이 고조파 감쇠가 자연적으로 감쇠되거나 이러한 목적을 위해 외부 필터가 추가되는 등 내재적인 저역 통과 또는 대역 통과 특성을 가질 수 있기 때문이다. SIDF 기법의 중요한 적용은 사인파 전자 오실레이터의 진동 진폭을 추정하는 것이다.

지금까지 사용된 다른 유형의 기술 기능은 수준 입력과 가우스 소음 입력에 대한 DF이다. 시스템에 대한 완전한 설명은 아니지만, DF는 종종 제어와 안정성에 관한 구체적인 질문에 대답하기에 충분하다. DF 방법은 상대적으로 비선형성이 약한 시스템을 분석하는 데 가장 적합하다. 기능(HOSIDF)을 설명하는 고차량의 사인파 입력을 추가하여 사인파 입력 주파수의 고조파에서 비선형 시스템 클래스의 응답을 설명한다. HOSIDF는 응답에서 비선형성이 유의미한 시스템에 대한 SIDF의 확장이다.

주의사항

기술 기능 방법은 광범위한 시스템에 대해 상당히 정확한 결과를 산출할 수 있지만, 다른 시스템에서는 나쁘게 실패할 수 있다. 예를 들어, 시스템이 비선형성의 더 높은 고조파를 강조하면 방법이 실패할 수 있다. 이러한 예는 Tzypkin이 뱅뱅 시스템을 위해 제시한 것이다.^[4] 상당히 유사한 예로는 비삽입형 Schmitt 트리거로 구성된 폐쇄 루프 오실레이터와 Schmitt 트리거의 입력으로 출력을 피드백하는 인버팅 통합 장치로 구성된다. Schmitt 트리거의 출력은 사각 파형이 되는 반면, 통합자의 출력은 사각 파형의 전환과 일치하는 피크가 있는 삼각 파형이 된다. 이 두 오실레이터 단계는 각각 신호를 정확히 90도만큼 지연시킨다(입력 대비). 만일 이 회로에 대해 DF 분석을 수행한다면, Schmitt 트리거의 입력에 있는 삼각파는 그것의 기본(사인파)으로 대체될 것이고, 이것은 트리거를 통과하는 위상변동을 90도 이하의 (사인파가 삼각파보다 빨리 트리거하기 때문에) 발생하게 되어 시스템이 Osci에 나타나지 않게 될 것이다.같은 방법으로 ^[5]부르다

또한 아이저만이나 칼만 추측의 조건이 충족되는 경우에는 함수법을 기술하여 주기적인 해결책이 없지만,^[6][7] 숨겨진 주기적인 유인기가 있는 백반샘플은 알려져 있다. 정지 세그먼트가 예측 한계 주기를 파괴할 때 불연속 동적 시스템에 대해 기술 함수 방법의 백플을 구성할 수 있다.^[8] 따라서 기술함수법의 적용은 추가적인 정당성을 필요로 한다.^[9][10]

참조

추가 읽기

외부 링크

• 전기 공학 백과사전: 기능 설명