에레스만 접속

미분 기하학에서 에레스만 연결(이 개념을 처음 공식화한 프랑스 수학자 샤를 에레스만 이후)은 연결 개념의 한 버전인데, 어떤 매끄러운 섬유 묶음에서도 이치에 맞는다. 특히, 기초 섬유 번들의 가능한 벡터 번들 구조에 의존하지 않지만, 그럼에도 불구하고, 선형 연결은 특별한 경우로 볼 수 있다. Ehresmann 연결의 또 다른 중요한 특별한 경우는 주요 번들에 대한 주요 연결로, 주요 Lie 그룹 동작에서 등가성이 있어야 한다.

소개

미분 기하학의 공변량 파생상품은 공변량 방식으로 벡터 번들 섹션의 방향성 파생상품을 취하는 선형 미분 연산자다. 또한 벡터 방향으로 번들의 평행 섹션의 개념을 공식화할 수 있게 해준다. 단면 s는 벡터 X를 ${\displaystyle \mathrm{따라}}$ ${\displaystyle {평행}_{}}$하다. $\nabla {\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ = 0$[\displaystyle \nabla _{X}s=0}.$ 따라서 공변량 파생상품은 최소한 두 가지를 제공한다$.$ 즉, 미분 연산자와 각 방향에서 평행하다는 것이 무엇을 의미하는지에 대한 개념이다. Ehresmann 연결은 차동 연산자를 완전히 떨어뜨리고 각 방향에서 평행한 섹션(Ehresmann 1950)의 측면에서 자명하게 연결을 정의한다. 구체적으로, Ehresmann 연결은 각 접선 공간의 벡터 서브공간을 수평공간이라 불리는 섬유다발의 총공간으로 단면화한다. 단면 ${\displaystyle s}$는 $d{\displaystyle \mathrm{}}$ (${\displaystyle }$X${\displaystyle }$) {\$displaystyle {\rm {d}s($X)}이(가$$) 수평 공간에 있는 경우 X 방향으로 수평(${\displaystyle 즉}$, 평행)이 된다. 여기서는 s를 $base{\displaystyle }$M에서 Fiber bundle E까지 함수 ${\displaystyle s}$로 한다 : ${\displaystyle M}$→ E ${\displaystyle s\colon M\to E},$ $d{\displaystyle \mathrm{}}$: ${\displaystyle T}$ ${\displaystyle M}$→ ${\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$ ${\displaystyle {}^{}}$ E ${\d$}s${\rm {d}s\colon$ TM\tom\$to s^*}$$TE}$은(는) 접선 벡터의 푸시 포워드다$$. 수평 공간은 함께 $T{\displaystyle }$ ${\displaystyle E}$ ${\displaystyle TE}$의 벡터 서브번들을 형성한다$.$

이것은 단순한 벡터 묶음보다 훨씬 더 넓은 종류의 구조물에서 정의될 수 있다는 즉각적인 이점이 있다. 특히 일반 섬유 묶음 위에 잘 정의되어 있다. 더욱이 공변량 파생상품의 많은 특징들은 여전히 남아있다: 평행 운송, 곡률, 그리고 홀로노미.

연결의 누락된 성분은 선형성과는 별개로 공분산이다. 전통적인 공변량 파생상품의 경우 공분산은 파생상품의 후향적 특성이다. 구성에서 공변량이 아닌 크리스토펠 기호의 변환 법칙을 명시하고, 파생상품의 일반적인 공분산 결과는 다음과 같다. 에레스만 접속의 경우, 섬유다발의 섬유에 작용하는 리 그룹을 도입함으로써 처음부터 일반화된 공분산 원리를 부과하는 것이 가능하다. 적절한 조건은 어떤 의미에서 수평 공간이 그룹 작용과 관련하여 등가변성을 갖도록 요구하는 것이다.

Ehresmann 연결의 마무리 터치는 연결 양식의 경우와 거의 같은 방식으로 차동 형태로 표현될 수 있다는 것이다. 집단이 섬유에 작용하여 연결이 등가성인 경우 형태도 등가성이 된다. 또한 연결 형태는 곡면성을 곡면성 형태로도 정의할 수 있다.

형식 정의

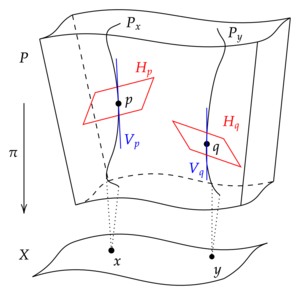
$\pi {\displaystyle }$: ${\displaystyle E}$→ ${\displaystyle M}$ ${\displaystyle \pi \colon E\to M}$을(를) 매끄러운 섬유 묶음이 되게$$ 하라.^[1] 내버려두다

${\displaystyle V=\ker(\operatorname {d} \pi \colon TE\to TM)}$

be the vertical bundle consisting of the vectors "tangent to the fibers" of E, i.e. the fiber of V at ${\displaystyle e\in E}$ is ${\displaystyle V_{e}=T_{e}(E_{\pi (e)})}$. This subbundle of ${\displaystyle TE}$ is canonically defined even when there is no canonical subspace tangent to 기준 공간 M. (물론, 이 비대칭은 섬유 묶음의 정의에서 비롯되는데, 이 정의는 "투영법 하나만 있다"${\displaystyle \pi }$ : E${\displaystyle }$→ ${\displaystyle M}$ ${\displaystyle \colon E\to$ M$},$ 제품$$ $E{\displaystyle }$= ${\displaystyle M}$ ${\displaystyle \times }$ ${\displaystyle F}$ ${\displaysty E=M\times F}$이 두 개일 것이다$$.)

수평 하위 공간을 통한 정의

E의 Ehresmann 연결은 $직접{\displaystyle }$ 합${\displaystyle \mathrm{분해}}$ ${\displaystyle T}$ E${\displaystyle }$= ${\displaystyle H}$ $\$ V {\$displaystyle TE=H=oplus$ V$}($Kola defines, Michor & Slovak 1993)을 정의한다는 점에서 연결의 수평 번들로 불리는 $T{\displaystyle }$ ${\displaystyle E}$ ${\displaystyty TE}$의 부드러운 하위 번들 H이다$.$ 좀 더 자세히 설명하면 가로다발에는 다음과 같은 속성이 있다.

• 각 지점 $e{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle E}$ ${\displaystyle e_in E}$에$$대해 H ${\displaystyle e_{}}$ ${\$는 e에서 $접선{\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ T$$E {\$displaystyle T_{$e}E$}$의 벡터 하위 공간이며$$, e에서 연결부의 수평 하위 공간이라고 불린다.
• ${\displaystyle H_{}}$ ${\displaystyle e_{}}$ ${\$는 e에 매끄럽게 의존한다$$.
• ${\displaystyle 각}$ $e{\displaystyle }$ ${\displaystyle \in }$ E ${\displaystyle e\in E}$에 대해$$$H{\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle V_{}}$ e${\displaystyle {}_{}}$=${\displaystyle }${ 0${\displaystyle }$} ${\displaystyle H_{e}\cap V_{e}=\{0$
• TE의_e 접선 벡터(모든 e∈E의 경우)는 수평 및 수직 구성요소의 합이므로 TE_ee = H + V_e.

보다 정교한 용어로, 이러한 특성을 만족하는 수평 공간의 배정은 제트 번들 JE¹ → E의 매끄러운 섹션에 정확하게 대응한다.

연결 양식을 통한 정의

마찬가지로 v를 H를 따라 수직 번들 V에 투영되도록 한다(H = ker v). 이는 TE를 수평 및 수직 부분으로 직접 분해하는 위의 총합에 의해 결정되며, 때로는 에레스만 연결부의 연결 형태라고 불리기도 한다. 따라서 v는 다음과 같은 특성(일반적으로 투영)을 갖는 TE에서 그 자체로 벡터 번들 동형성이다.

• v² = v;
• v는 V=Image(v)의 ID이다.

반대로 v가 이 두 특성을 만족하는 TE의 벡터 번들 내형성인 경우, H = ker v는 Ehresmann 연결의 수평 서브번들이다.

마지막으로, v는 각 접선 공간을 그 자체로 선형 매핑하는 것으로서 E에서 TE 값 1-폼으로도 간주될 수 있다. 이것은 앞으로의 부분에서 유용한 관점이 될 것이다.

수평 리프트를 통한 병렬 운송

또한 Ehresmann 연결부는 곡선까지의 접선이 수평이 되도록 베이스 다지관 M에서 섬유 다발 E의 총 공간으로 곡선을 들어올리는 방법을 규정한다.^[2] 이러한 수평 리프트는 연결 형식주의 다른 버전에 대한 병렬 수송의 직접적인 아날로그다.

구체적으로 γ(t)가 점 x = γ(0)을 통과하는 M의 부드러운 곡선이라고 가정한다. e ∈ E를_x x에 걸쳐 섬유 속의 한 점이 되게 하라. γ ~${\displaystyle }$( t${\displaystyle }$) ${\displaystyle${\$tilde{\gamma }}}(t)$는 전체 공간 E에서$$ 다음과 같이 $\gamma {\displaystyle \stackrel{}{}}$ ~${\displaystyle \stackrel{}{}}$( ${\displaystyle t}$)의 곡선이다.

${\displaystyle \stackrel{}{\gamma }}$~${\displaystyle }$( ${\displaystyle 0}$)${\displaystyle }$= ${\displaystyle e}$ ${\displaystyle {\tilde {\\tilde}}=e},$${\displaystyle \pi \stackrel{}{}}$~ (${\displaystyle t}$)${\displaystyle }$=${\displaystyle \gamma }$ ( ${\displaystyle t}$ ) = γ$\displaystyle \pi({\tilde{\tilde})(t)$$=\cHB(t)$$}$

추가로, 곡선의 모든 접선이 TE의 수평 하위 분들에 있는 경우 리프트는 수평이다.

${\displaystyle {\tilde {\gamma }}(t)\in H_{\tilde {\gamma }}.$

It can be shown using the rank–nullity theorem applied to π and v that each vector X∈T_xM has a unique horizontal lift to a vector ${\displaystyle {\tilde {X}}\in T_{e}E}$. In particular, the tangent field to γ generates a horizontal vector field in the total space of the pullback bundle γ*E. 피카르-린델뢰프 정리로는 이 벡터장을 통합할 수 있다. 따라서, 어떤 곡선 and과 x = ((0) 위의 점 e에 대해, 작은 시간 t 동안 γ ~ e의 독특한 수평 리프트가 존재한다.

일반적인 Ehresmann 연결의 경우 수평 리프트는 경로에 의존한다. γ₁(0) = γ₂(0) = x에₀ 일치하고 다른 지점₁ x ∈ M에서 교차하는 M의 두 부드러운 곡선이 동일한 e e π⁻¹(x₀)를 통해 E로 수평으로 들어올리면 일반적으로 π⁻¹(x₁)의 다른 지점을 통과하게 된다. 이것은 섬유 묶음의 차등 기하학에 중요한 결과를 가져온다: H의 섹션의 공간은 벡터 필드의 리 브라켓 아래에서 (일반적으로) 닫히지 않기 때문에 E에 있는 벡터 필드의 공간에 대한 리 하위 지오브라가 아니다. Lie Bracket에 따른 이러한 폐쇄 실패는 곡률에 의해 측정된다.

특성.

곡률

V를 에레스만과 연결시켜라. 그 다음 v의 곡면성은 다음과^[3] 같이 주어진다.

${\displaystyle R={\tfrac {1}{1}:{2}}[v,v]}$

여기서 [-,-]는 v v Ω¹(E,TE)의 Frölicher-Nijenhuis 브래킷을 나타낸다. 따라서 R ∈ Ω²(E,TE)은 E에 대한 두 가지 형태로서 TE에 의해 정의된다.

${\displaystyle R}$( ${\displaystyle X}$, Y${\displaystyle }$)${\displaystyle }$= ${\displaystyle v}$(${\displaystyle }$(${\displaystyle }$i ${\displaystyle \mathrm{d}}$- v${\displaystyle }$) ${\displaystyle X}$,${\displaystyle }$( ${\displaystyle \mathrm{i}}$ ${\displaystyle d\mathrm{}}$- ${\displaystyle v}$) ${\displaystyle Y}$ ${\$, $(\mathrm {id} -v)Y]\right)}$ $,,$

아니면 다른 말로 하면

${\$$\{$$V},$

여기서 X = X_H + X는_V 각각 H 성분과 V 성분으로 직접 합 분해를 나타낸다. 곡률에 대한 이 마지막 표현에서, 만약 수평 하위 분개가 프로베니우스 통합이 가능하다면, 그리고 만약 그렇다면, 똑같이 사라지는 것으로 보인다. 따라서 곡면성은 수평 서브분들에 대한 통합성 조건으로서 섬유다발 E → M의 횡단면을 산출한다.

Ehresmann 연결의 곡면성은 또한 Bianchi ID의 버전을 만족한다.

$왼쪽[v,R\오른쪽]=0}$

여기서 다시 [-,-]는 v ∈ Ω¹(E,TE) 및 R ∈ Ω²(E,TE)의 Frölicher-Nijenhuis 브래킷이다.

완성도

에레스만 연결은 곡선이 국부적으로 독특한 수평 리프트를 가질 수 있도록 한다. 완전한 Ehresmann 연결의 경우, 곡선은 전체 영역 위로 수평으로 들어올릴 수 있다.

홀로노미

연결의 평탄도는 수평 공간의 프로베니우스 통합성에 국소적으로 해당한다. 다른 극단에서 비반사성 곡률은 연결부의 홀노믹의 존재를 의미한다.^[4]

특례

주 번들 및 주 연결

E가 M에 대한 원만한 G번들이라고 가정하자. 그 다음에 E에 대한 G 작용과 관련하여 E에 대한 E에 대한 Ehresmann 연결 H가 불변하는 경우, 주(Ehresmann) 연결이라고^[5] 한다.

${\displaystyle H_{eg}=\mathrm {d} (R_{g})_{e}(H_{e})}$ for any e∈E and g∈G; here ${\displaystyle \mathrm {d} (R_{g})_{e}}$ denotes the differential of the right action of g on E at e.

G의 1-모수 부분군은 E에 수직으로 작용한다. 이 동작의 차등화를 통해 그룹 ${\displaystyle G_{}}$의 Lie 대수 g로$$ 하위 공간 V $e{\displaystyle {}_{}}$ ${\$을(를) 식별할 수 있다. 예를 들어 지도${\displaystyle }\iota {\displaystyle }$ : ${\displaystyle V\mathfrak{}}$ ${\displaystyle e_{}}$→ g ${\$ 그런 다음 Ehresmann 연결의 연결 양식 v는 Ω(X)=ι(v(X)로 정의된 g 값을 가진 E의 1-form Ω으로 볼 수 있다.

따라서 재해석된 연결 형태 Ω은 다음과 같은 두 가지 특성을 만족시킨다.

• It transforms equivariantly under the G action: ${\displaystyle R_{h}^{*}\omega ={\hbox{Ad}}(h^{-1})\omega }$ for all h∈G, where R_h^* is the pullback under the right action and Ad is the adjoint representation of G on its Lie algebra.
• 수직 벡터 필드를 모든 X allV에 대해 리 대수 관련 요소: Ω(X)= associated(X)에 매핑한다.

반대로, 주요 번들에 있는 그러한 g-값 1-폼은 앞에서 언급한 특성을 만족시키는 수평 분포를 발생시킨다는 것을 보여줄 수 있다.

국소적인 사소한 것이 주어지면 수평 벡터 필드(이 사소한 것에서) Ω을 줄일 수 있다. 풀백을 통해 B에 1-폼 Ω'을 정의한다. Ω' 형식은 Ω을 완전히 결정하지만, 사소한 것의 선택에 달려 있다. (이 형태는 흔히 연결 형태라고도 하며 간단히 Ω으로 표시된다.)

벡터 번들 및 공변량 파생 모델

E가 M 위에 있는 매끄러운 벡터 번들이라고 가정하자. 그 후 H가_e 각 x ∈ M에 대해 e ∈ E에_x 선형적으로 의존하는 경우 E의 Ehresmann 연결 H는 선형(Ehresmann) 연결이라고 한다. 이를 정확히 하기 위해 S는_λ E에 λ으로 메스 곱셈을 나타내도록 한다. 그 다음 ${\displaystyle H_{}}$는 모든 e ∈${\displaystyle {}_{}{e}_{}}$ = ${\displaystyle d\mathrm{}}$ ( ${\displaystyle S_{}{}_{}{}_{}}$ ) ${\displaystyle e_{}}$( ${\displaystyle {}_{}{e}_{}}$ ) ${\displaystyle H_{\lambda$ e$}=\mathrm {d}(S_{\lambda }}}}_{e}(H_{e})$에 대해$$ 선형이다.

E는 벡터 번들이기 때문에, 그것의 수직 번들 V는 π*E에 이형이다. 따라서 s가 E의 섹션인 경우 v(ds):TM→s*V=s*s*ss*E=E. 벡터 번들 형태론이며, 따라서 벡터 번들 Hom(TM,E)의 섹션 ∇s에 의해 주어진다. The fact that the Ehresmann connection is linear implies that in addition it verifies for every function ${\displaystyle f}$ on ${\displaystyle M}$ the Leibniz rule, i.e. ${\displaystyle \nabla (fs)=f\nabla (s)+d(f)\otimes s}$, and therefore is a covariant derivative of s.

반대로 벡터 번들의 공변량 파생상품 ∇은 H를_e 정의하여 선형 Ehresmann 연결을 정의하며, 여기서 s는 모든 X ∈ TM에_xx 대해 s(x) = e, ∇_Xs = 0인 E의 섹션이다_x.

(역사적 이유로) 연결에 적용할 때 선형이라는 용어는 접선 번들이나 프레임 번들에 정의된 연결을 참조하기 위해 (부착이라는 단어와 마찬가지로) 가끔 사용된다.

관련 번들

섬유 묶음(구조 그룹에 부여된)의 Ehresmann 연결은 때때로 관련 묶음에서 Ehresmann 연결을 발생시킨다. 예를 들어, 벡터 번들 E에서 (선형) 연결은 위에서와 같이 E의 평행성을 주는 것으로 생각되며, E의 관련 프레임 PE 번들에 연결을 유도한다. 반대로, PE의 연결이 프레임에 대한 일반 선형 그룹의 작용(따라서 주된 연결)과 관련하여 등가선인 경우, PE의 연결은 E의 (선형) 연결을 발생시킨다. Ehresmann 연결이 관련된 묶음에서 자연스럽게 연결되도록 유도하는 것은 항상 가능한 것은 아니다. 예를 들어 벡터 번들의 프레임 묶음에 비등가 Ehresmann 연결은 벡터 번들에 대한 연결을 유도하지 않을 수 있다.

E가 P의 관련 묶음이기 때문에 E = P ×_G F. E의 G 연결은 E의 병렬 전송 지도 τ : F_x → F가_x′ 섬유의 G-변환에 의해 주어지는 Ehresmann 연결이라고 가정한다(^[6]곡선으로 결합한 M의 충분히 가까운 지점 x와 x′).

P에 대한 주 연결부가 주어지면 풀백을 통해 관련 섬유다발 E = P ×_G F에 대한 G 연결을 얻는다.

반대로 E에 대한 G-연결로 인해 관련 기본 번들 P에 대한 주 연결을 복구할 수 있다. 이러한 주요 연결을 복구하기 위해 일반적인 F섬유의 프레임 개념을 도입한다. G는 F에 효과적으로 작용하는 유한차원^[7] Lie 그룹이기 때문에, G-orbit R = {(gy₁,...,gy_m) g ∈ G}이 G의 주요 동질 공간일 정도로 F 내에 점(y,...,y₁)의_m 유한 구성이 존재해야 한다. R은 F에 대한 G 액션을 위한 프레임 개념을 일반화한 것이라고 생각할 수 있다. R은 G에 대한 주된 동질 공간이기 때문에, 일반적인 섬유 R과 E와 관련된 섬유 번들 E(R)는 E와 관련된 주요 번들과 (같다)라는 점에 유의한다. 그러나 그것은 또한 E의 m-폴드 제품 묶음의 하위 번들이기도 하다. E의 수평 공간 분포는 이 제품 번들의 공간 분포를 유도한다. 연결과 연관된 병렬 전송 맵은 G-맵이므로 서브 스페이스 E(R)를 보존하므로 G-연결은 E(R)의 주 G-연결부로 내려간다.

요약하면, 관련 섬유 번들에 대한 주요 연결의 하강과 관련 섬유 번들에 대한 G 연결 사이에 일대일 일치(최대 동등성)가 있다. 이러한 이유로, 구조 그룹 G가 있는 섬유 번들의 범주에서, 주 연결은 관련 번들의 G 연결에 관한 모든 관련 정보를 포함한다. 따라서 관련 번들에 대한 연결을 고려해야 할 중요한 이유가 없는 한(예: Cartan 연결의 경우) 일반적으로 주된 연결과 직접 작용한다.

메모들

참조

• Ehresmann, Charles (1950), Les connexions infinitésimales dans un espace fibré différentiable, Colloque de Topologie, Bruxelles, pp. 29–55
• Eliason, H (1967), "Geometry of manifolds of maps", Journal of Differential Geometry, 1: 169–194
• Kobayashi, Shoshichi; Nomizu, Katsumi (1996), Foundations of Differential Geometry, Vol. 1 (New ed.), Wiley-Interscience, ISBN 0-471-15733-3 volume= 추가 텍스트(도움말)
• Kobayashi, Shoshichi; Nomizu, Katsumi (1996), Foundations of Differential Geometry, Vol. 2 (New ed.), Wiley-Interscience, ISBN 978-0-471-15732-8 volume= 추가 텍스트(도움말)
• Kolář, Ivan; Michor, Peter; Slovák, Jan (1993), Natural operators in differential geometry (PDF), Springer-Verlag, archived from the original (PDF) on 2017-03-30, retrieved 2007-04-25
• Lang, Serge (1999), Fundamentals of differential geometry, Springer-Verlag, ISBN 0-387-98593-X
• Lumiste, Ülo (2001) [1994], "Connection on a fibre bundle", Encyclopedia of Mathematics, EMS Press
• Lumiste, Ülo (2001) [1994], "Connections on a manifold", Encyclopedia of Mathematics, EMS Press
• Reeb, Georges (1952), Sur certaines propriétés topologiques des variétés feuilletées, Paris: Herman

추가 읽기

• Raoul Bott(1970) "통합성에 대한 위상적 방해", Proc. 동정심. 순수한 수학, 16 에이머. 수학, 소코, 프로비던스, 리알.