앙상블 예측

Ensemble forecasting
Top: 허리케인 Rita 트랙의 기상 조사 및 예보 모델 시뮬레이션.하단:국립허리케인센터 멀티모델 앙상블 예보 확산

앙상블 예측은 수치적 기상 예측에서 또는 수치적 기상 예측 내에서 사용되는 방법이다.가장 가능성이 높은 날씨를 단일 예측으로 예측하는 대신 일련의 예측(또는 합체)이 생성됩니다.이 일련의 예보는 대기 중 미래 가능한 상태의 범위를 나타내는 것을 목적으로 한다.앙상블 예측은 몬테카를로 분석의 한 형태이다.예측 모델에서 불확실성의 일반적인 두 가지 원인을 설명하기 위해 다중 시뮬레이션이 수행된다. (1) 불완전한 초기 조건의 사용에 의해 도입된 오차, 그리고 (2) 초기 조건에 대한 민감한 의존성으로 종종 언급되는 대기 진화 방정식의 혼돈한 특성으로 증폭된 오차.방정식을 푸는 근사 수학적 방법과 같은 모형 공식의 불완전성 때문에 생성되었습니다.검증된 미래 대기 상태는 예측된 앙상블 확산 범위 내에 있어야 하며 확산량은 예측의 불확실성(오차)과 관련되어야 한다.일반적으로 이 접근방식은 날씨 예측뿐만 아니라 동적 시스템의 확률론적 예측을 위해 사용할 수 있다.

인스턴스

오늘날 앙상블 예측은 다음과 같은 전 세계 주요 운영 기상 예측 시설에서 일반적으로 이루어집니다.

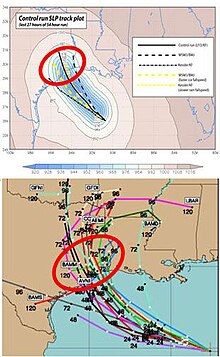
실험적인 앙상블 예측은 워싱턴 대학과 같은 여러 대학에서 이루어지며, 미국의 앙상블 예측은 미국 해군과 공군에 의해서도 생성된다.스파게티 플롯, 앙상블 수단, 우편 스탬프 등 다양한 방법으로 데이터를 볼 수 있습니다.이러한 방법에서는, 실행한 모델의 다양한 결과를 비교할 수 있습니다.

역사

다음 항목도 참조하십시오.수치예보의 역사

1963년 에드워드 로렌츠가 제안한 바와 같이,[1] 2주 이상 전에 만들어진 장기 예측은 관련된 유체 역학 방정식의 혼돈한 특성 때문에 어떠한 기술로도 대기 상태를 예측하는 것은 불가능하다.또한 기존 관측 네트워크는 제한된 공간 및 시간 분해능(예: 태평양과 같은 큰 수역)을 가지고 있어 대기의 진정한 초기 상태에 불확실성을 초래한다.Liouville 방정식으로 알려진 일련의 방정식은 모델 초기화의 초기 불확실성을 결정하기 위해 존재하지만, 방정식은 슈퍼컴퓨터를 [2]사용하더라도 실시간으로 실행하기에는 너무 복잡합니다.앙상블 예측의 실질적인 중요성은 혼란스럽고 비선형적인 시스템에서 예측 오차 증가율이 시작 조건에 따라 결정된다는 사실에서 비롯된다.따라서 앙상블 예측은 상태 의존적 예측가능성의 사전 추정치, 즉 예측 초기 조건의 불가피한 불확실성과 방정식의 계산 표현의 정확성에 주어진 발생 가능한 날씨 유형의 추정치를 제공한다.이러한 불확실성으로 인해 예측 모델의 정확도가 향후 [3]약 6일로 제한됩니다.첫 [4]번째 운영 앙상블 예측은 1985년에 서브시즌 타임스케일에 대해 작성되었다.그러나 그러한 예측을 뒷받침하는 철학은 이전에는 순전히 결정론적 수단으로 예측이 이루어졌던 짧은 기간에도 관련이 있다는 것을 깨달았다.

에드워드 엡스타인은 1969년 고유 불확실성으로 인해 단일 예측 실행으로 대기를 완전히 묘사할 수 없다는 것을 인식하고 대기 [5]상태에 대한 평균과 분산을 생성하는 확률적 동적 모델을 제안했다.이러한 몬테카를로 시뮬레이션은 기술을 보여주었지만, 1974년 Cecil Leith는 앙상블 확률 분포가 대기 [6]중 확률 분포의 대표적인 표본일 때만 적절한 예측을 산출했다고 밝혔다.1992년이 되어서야 유럽 중거리 일기 예보 센터(ECMWF)와 국립 환경 예측 센터(NCEP)가 앙상블 예보를 준비하기 시작했다.

불확실성을 나타내는 방법

합체 일기 예보를 할 때 고려해야 할 불확실성의 주요 원천은 두 가지가 있다. 즉, 초기 조건 불확실성과 모델 [7]불확실성이다.

초기 조건 불확실성

초기 조건 불확실성은 대기의 제한된 관측과 위성 데이터와 같은 간접 측정의 사용에 관련된 불확실성으로 인해 예보에 대한 시작 조건 추정의 오류로 인해 발생한다.초기 조건의 불확실성은 다른 앙상블 부재 간의 시작 조건을 교란함으로써 나타난다.이는 과거의 진화와 함께 대기의 현재 상태에 대한 우리의 지식과 일치하는 시작 조건의 범위를 탐색합니다.이러한 초기 조건 섭동을 생성하는 방법은 여러 가지가 있습니다.ECMWF 모델인 앙상블 예측 시스템(EPS)[8]은 단수 벡터와 앙상블 데이터 동화(EDA)의 조합을 사용하여 초기 확률 [9]밀도를 시뮬레이션합니다.단수 벡터 섭동은 외부 트랙에서 더 활발한 반면, EDA 섭동은 열대 지역에서 더 활발하다.NCEP 앙상블인 Global Ensemble Forecasting System은 벡터 [10][11]사육이라고 알려진 기술을 사용합니다.

모델의 불확도

모델 불확실성은 예측 모델의 한계로 인해 발생합니다.컴퓨터 모델에서 대기를 표현하는 과정은 예측에 오류를 가져오는 매개 변수 설정 체계 개발과 같은 많은 단순화를 수반한다.모델 불확실성을 나타내는 몇 가지 기법이 제안되었다.

교란된 파라미터 방식

파라미터 설정 스킴을 개발할 때 단순화된 물리적 프로세스를 나타내기 위해 많은 새로운 파라미터가 도입됩니다.이들 파라미터는 매우 불확실할 수 있습니다.예를 들어, '엔터테인먼트 계수'는 건조한 환경 공기가 대류 구름에 난류 혼합되는 것을 나타내며, 따라서 단일 숫자를 사용하는 복잡한 물리적 프로세스를 나타냅니다.섭동 파라미터 접근법에서는 모델의 파라미터 설정 스킴에서 불확실한 파라미터가 식별되어 앙상블 멤버 간에 값이 변화한다.climateprediction.net과 같은 확률론적 기후 모델링에서는 이러한 매개변수가 전 세계적으로 일정하게 유지되는 경우가 많지만,[12] 현대 수치 기상 예측에서는 시공간에서 [13]매개변수의 값을 확률적으로 변경하는 것이 더 일반적이다.매개변수 섭동의 정도는 전문가의 [14]판단을 사용하거나 주어진 [15]모델에 대한 매개변수 불확실성의 정도를 직접 추정하여 유도할 수 있다.

확률적 모수

기존 매개변수 분석 체계는 분해된 척도 상태(예: 대규모 온도 및 바람장)에 대한 하위 그리드 스케일 움직임(예: 대류 구름)의 평균 효과를 나타내려고 한다.확률적 파라미터화 스킴은 특정 분해 스케일 상태와 일치하는 많은 서브 그리드 스케일 상태가 있을 수 있음을 인식한다.가장 가능성이 높은 하위 그리드 스케일 움직임을 예측하는 대신, 확률적 매개변수화 체계는 하위 그리드의 실현 가능한 한 가지 실현을 나타낸다.이것은 운동 방정식에 난수를 포함시킴으로써 이것을 한다.이 표본은 불확실한 공정에 할당된 확률 분포에서 추출됩니다.확률적 매개변수는 기상 예측 모델의 기술을 크게 향상시켰고, 현재 전 [16]세계 운영 예측 센터에서 사용되고 있다.확률적 매개변수는 유럽 중거리 기상 [17]예보 센터에서 처음 개발되었다.

멀티모델 앙상블

예측 생성을 위해 많은 다른 예측 모델을 사용하는 경우, 이 접근방식을 다중 모델 앙상블 예측이라고 한다.이 예측 방법은 단일 모델 기반 [18]접근법에 비해 예측을 개선할 수 있습니다.다중 모델 앙상블 내의 모델이 다양한 바이어스에 맞게 조정되는 경우, 이 프로세스를 "수페렌블 예측"이라고 합니다.이러한 유형의 예측은 모형 [19]출력의 오류를 상당히 줄여줍니다.대기, 해양 및 파동 모델의 조합과 같이 서로 다른 물리적 과정의 모델이 결합될 때, 다중 모델 앙상블은 하이퍼 [20]앙상블이라고 불립니다.

확률 평가

앙상블 예측은 일반적으로 한 예측 변수에 대한 개별 예측의 앙상블 평균을 해당 변수의 관측 값과 비교함으로써 평가된다("오류")이는 앙상블 시스템 내의 다양한 예측 간의 일치 정도를 고려하여 전체 표준 편차 또는 "확산"으로 표현된다.앙상블 확산은 스파게티 다이어그램과 같은 도구를 통해 시각화할 수 있으며, 이는 미래의 특정 시간 단계에 대한 예후 차트에서 한 수량의 분산을 보여준다.앙상블 확산이 사용되는 또 다른 도구는 기상도입니다. 기상도는 한 특정 위치에 대한 한 수량의 예측 분산을 보여줍니다.앙상블 확산이 너무 작아서 관측된 대기 상태가 앙상블 예측 범위를 벗어나는 것이 일반적이다.이것은 기상캐스터가 그들의 [21]예보에 과신하게 만들 수 있다.이 문제는 특히 예측에서 모델 불확실성을 고려하지 않는 경우 약 10일 [22]전의 날씨 예측에서 특히 심각해진다.

신뢰성과 해상도(보정 및 선명도)

앙상블 예측의 확산은 기상 캐스터가 자신의 예측에 얼마나 자신감을 가질 수 있는지를 나타냅니다.앙상블 산포도가 작고 예측 솔루션이 여러 모형 런 내에서 일관성이 있는 경우 기상 캐스터는 일반적으로 [21]예측에 대한 신뢰도가 더 높아집니다.확산이 크면 예측이 더 불확실하다는 것을 나타냅니다.이상적으로는 확산-기술 관계가 존재해야 하며, 따라서 앙상블의 확산은 앙상블 평균에서 예상되는 오차의 좋은 예측 변수입니다.예측이 신뢰할 수 있는 경우 관측된 상태는 예측 확률 분포에서 도출된 것처럼 작동합니다.신뢰성(또는 교정)은 앙상블 평균 오차의 표준 편차를 예측 범위와 비교하여 평가할 수 있다. 신뢰성 있는 예측을 위해서는 서로 다른 예측 리드 타임과 서로 다른 위치에 [23]대해 둘 다 일치해야 한다.

특정 기상 이벤트의 예측 신뢰도 평가할 수 있습니다.예를 들어, 50명 중 30명이 다음 24시간 동안 1cm 이상의 강우량을 보인다면, 1cm를 초과할 확률은 60%로 추정할 수 있다.예보는 60% 확률이 예측된 과거의 모든 상황을 고려할 때, 그 중 60%가 실제로 1cm를 초과하는 경우 신뢰할 수 있는 것으로 간주된다.실제로 운용 기상 앙상블 예측에서 생성된 확률은 신뢰성이 높지 않지만, 과거 예측(예보 또는 예측)과 관측치를 사용하여 앙상블의 확률 추정치를 조정하여 신뢰성을 높일 수 있다.

앙상블 예측의 또 다른 바람직한 특성은 분해능입니다.이는 예측이 기후학적 사건 빈도에서 얼마나 벗어나는지를 나타낸다. 앙상블이 신뢰할 수 있는 경우, 이 편차를 증가시키면 예측의 유용성이 증가한다.이 예측 품질은 선명도 또는 예측의 산포도가 얼마나 작은지도 고려할 수 있습니다.기상 캐스터의 주요 목표는 [24]신뢰성을 유지하면서 선명도를 극대화하는 것입니다.두 모델 상태 간의 예상 차이가 예측 모드로부터 두 랜덤 상태 간의 차이만큼 클 때까지 초기 조건의 불가피한(보통 작더라도) 오류가 예측 리드 증가와 함께 증가하기 때문에 긴 리드에서의 예측은 특별히 날카롭지 않을 수밖에 없다.엘의 기후학

앙상블 예측 교정

관측된 기상 변수의 확률을 예측하는 데 앙상블 예측을 사용하는 경우 일반적으로 편중되지 않고 신뢰할 수 있는 예측을 생성하기 위해 보정이 필요합니다.온도 예측의 경우 한 가지 간단하고 효과적인 교정 방법은 선형 회귀 분석이며, 이 상황에서는 모형 출력 통계량이라고 합니다.선형 회귀 모형은 앙상블 평균을 실제 온도의 예측 변수로 사용하고 평균 주위의 앙상블 부재의 분포를 무시하고 회귀 분석의 잔차 분포를 사용하여 확률을 예측합니다.이 교정 설정에서 예측 개선을 위한 앙상블의 값은 앙상블 평균이 일반적으로 단일 앙상블 구성원에 비해 더 나은 예측을 제공하는 것이며, 평균 주위의 앙상블 구성원의 분포 폭 또는 모양에 포함된 정보 때문이 아니다.그러나 2004년에 예측 분포의 폭을 제공하기 위해 앙상블 확산의 선형 변환을 사용하는 선형 회귀(현재는 비균질 가우스 회귀)의 일반화가 도입되었고[25], 이는 선형 회귀만을 기반으로 하는 것보다 더 높은 기술로 예측으로 이어질 수 있는 것으로 나타났다.이것은 처음으로 평균 주변 앙상블 부재의 분포 형태(이 경우 앙상블 확산으로 요약)의 정보를 선형 회귀에 대한 예측을 개선하는 데 사용할 수 있다는 것을 증명했다.앙상블 산포를 사용하여 선형 회귀 분석을 처리할 수 있는지 여부는 예측 시스템, 예측 변수 및 리드 타임에 따라 달라집니다.

예측 변경 크기 예측

앙상블 확산은 불확실성의 예측을 개선하는 데 사용될 뿐만 아니라 한 예측에서 다음 [26]예측으로 평균 예측의 가능한 변화의 크기에 대한 예측자로도 사용될 수 있다.일부 앙상블 예측 시스템에서는 좁은 앙상블이 평균의 작은 변화보다 선행하는 경향이 있는 반면 넓은 앙상블은 평균의 큰 변화보다 선행하는 경향이 있기 때문이다.이는 무역업계에서 응용이 가능하기 때문에 미래의 예측변화 규모를 파악하는 것이 중요하다.

공동 연구

주요 기사: SORPEX Interactive Grand Global Ensemble

관측 시스템 연구 및 예측 가능성 실험(TORPEX)은 사회, 경제 및 환경의 이익을 위해 하루에서 2주간의 높은 영향 일기 예보의 정확성을 개선하기 위한 10년 국제 연구 개발 프로그램이다.학술 기관, 운영 예측 센터 및 예보 제품 사용자 간의 국제 협력을 통해 솔루션을 가속화할 기상 연구 및 예측 문제를 다루는 조직 프레임워크를 확립한다.

주요 구성요소 중 하나는 인류의 이익을 위해 하루에서 2주간의 높은 영향을 미치는 일기예보의 정확성을 향상시키기 위한 세계 기상 연구 프로그램인 TORPEX Interactive Grand Global Ensemble(TIGGE)이다.많은 국제 센터에서 제공하는 앙상블 모델 예측 데이터의 중앙 집중식 아카이브는 광범위한 데이터 공유와 연구를 가능하게 하기 위해 사용됩니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Cox, John D. (2002). Storm Watchers. John Wiley & Sons, Inc. pp. 222–224. ISBN 978-0-471-38108-2.
  2. ^ Manousos, Peter (2006-07-19). "Ensemble Prediction Systems". Hydrometeorological Prediction Center. Retrieved 2010-12-31.
  3. ^ Weickmann, Klaus, Jeff Whitaker, Andres Roubicek 및 Catherine Smith(2001-12-01)앙상블 예보를 사용하여 중거리(3~15일)의 일기 예보를 개선합니다.기후 진단 센터.2007-02-16 취득.
  4. ^ Palmer, Tim (2018). "The ECMWF ensemble prediction system: Looking back (more than) 25 years and projecting forward 25 years". Quarterly Journal of the Royal Meteorological Society. arXiv:1803.06940. Bibcode:2018arXiv180306940P. doi:10.1002/qj.3383. ISSN 1477-870X. S2CID 4944687.
  5. ^ Epstein, E.S. (December 1969). "Stochastic dynamic prediction". Tellus A. 21 (6): 739–759. Bibcode:1969Tell...21..739E. doi:10.1111/j.2153-3490.1969.tb00483.x.
  6. ^ Leith, C.E. (June 1974). "Theoretical Skill of Monte Carlo Forecasts". Monthly Weather Review. 102 (6): 409–418. Bibcode:1974MWRv..102..409L. doi:10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2. ISSN 1520-0493.
  7. ^ Slingo, Julia; Palmer, Tim (2011-12-13). "Uncertainty in weather and climate prediction". Phil. Trans. R. Soc. A. 369 (1956): 4751–4767. Bibcode:2011RSPTA.369.4751S. doi:10.1098/rsta.2011.0161. ISSN 1364-503X. PMC 3270390. PMID 22042896.
  8. ^ "The Ensemble Prediction System (EPS)". ECMWF. Archived from the original on 2010-10-30. Retrieved 2011-01-05.
  9. ^ "Quantifying forecast uncertainty ECMWF". www.ecmwf.int. 2013-11-29. Retrieved 2016-11-20.
  10. ^ Toth, Zoltan; Kalnay, Eugenia (December 1997). "Ensemble Forecasting at NCEP and the Breeding Method". Monthly Weather Review. 125 (12): 3297–3319. Bibcode:1997MWRv..125.3297T. CiteSeerX 10.1.1.324.3941. doi:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2. ISSN 1520-0493.
  11. ^ Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. (January 1996). "The ECMWF Ensemble Prediction System: Methodology and validation". Quarterly Journal of the Royal Meteorological Society. 122 (529): 73–119. Bibcode:1996QJRMS.122...73M. doi:10.1002/qj.49712252905.
  12. ^ "Perturbed Physics Ensembles climateprediction.net". www.climateprediction.net. Retrieved 2016-11-20.
  13. ^ McCabe, Anne; Swinbank, Richard; Tennant, Warren; Lock, Adrian (2016-10-01). "Representing model uncertainty in the Met Office convection-permitting ensemble prediction system and its impact on fog forecasting". Quarterly Journal of the Royal Meteorological Society. 142 (700): 2897–2910. Bibcode:2016QJRMS.142.2897M. doi:10.1002/qj.2876. ISSN 1477-870X.
  14. ^ Ollinaho, Pirkka; Lock, Sarah-Jane; Leutbecher, Martin; Bechtold, Peter; Beljaars, Anton; Bozzo, Alessio; Forbes, Richard M.; Haiden, Thomas; Hogan, Robin J. (2016-10-01). "Towards process-level representation of model uncertainties: Stochastically perturbed parametrisations in the ECMWF ensemble". Quarterly Journal of the Royal Meteorological Society. 143 (702): 408–422. Bibcode:2017QJRMS.143..408O. doi:10.1002/qj.2931. ISSN 1477-870X.
  15. ^ Christensen, H. M.; Moroz, I. M.; Palmer, T. N. (2015-02-04). "Stochastic and Perturbed Parameter Representations of Model Uncertainty in Convection Parameterization". Journal of the Atmospheric Sciences. 72 (6): 2525–2544. Bibcode:2015JAtS...72.2525C. doi:10.1175/JAS-D-14-0250.1. ISSN 0022-4928.
  16. ^ Berner, Judith; Achatz, Ulrich; Batté, Lauriane; Bengtsson, Lisa; De La Cámara, Alvaro; Christensen, Hannah M.; Colangeli, Matteo; Coleman, Danielle R. B.; Crommelin, Daan (2016-07-19). "Stochastic Parameterization: Towards a new view of Weather and Climate Models". Bulletin of the American Meteorological Society. 98 (3): 565. arXiv:1510.08682. Bibcode:2017BAMS...98..565B. doi:10.1175/BAMS-D-15-00268.1. ISSN 0003-0007. S2CID 33134061.
  17. ^ Buizza, R.; Milleer, M.; Palmer, T. N. (1999-10-01). "Stochastic representation of model uncertainties in the ECMWF ensemble prediction system". Quarterly Journal of the Royal Meteorological Society. 125 (560): 2887–2908. Bibcode:1999QJRMS.125.2887B. doi:10.1002/qj.49712556006. ISSN 1477-870X.
  18. ^ Zhou, Binbin and Jun Du (February 2010). "Fog Prediction From a Multimodel Mesoscale Ensemble Prediction System" (PDF). Weather and Forecasting. 25 (1): 303. Bibcode:2010WtFor..25..303Z. doi:10.1175/2009WAF2222289.1. Retrieved 2011-01-02.
  19. ^ Cane, D. and M. Milelli (2010-02-12). "Multimodel SuperEnsemble technique for quantitative precipitation forecasts in Piemonte region". Natural Hazards and Earth System Sciences. 10 (2): 265. Bibcode:2010NHESS..10..265C. doi:10.5194/nhess-10-265-2010.
  20. ^ Vandenbulcke, L.; et al. (2009). "Super-Ensemble techniques: application to surface drift prediction" (PDF). Progress in Oceanography. 82 (3): 149–167. Bibcode:2009PrOce..82..149V. doi:10.1016/j.pocean.2009.06.002.
  21. ^ a b Warner, Thomas Tomkins (2010). Numerical Weather and Climate Prediction. Cambridge University Press. pp. 266–275. ISBN 978-0-521-51389-0.
  22. ^ Palmer, T.N.; G.J. Shutts; R. Hagedorn; F.J. Doblas-Reyes; T. Jung; M. Leutbecher (May 2005). "Representing Model Uncertainty in Weather and Climate Prediction". Annual Review of Earth and Planetary Sciences. 33: 163–193. Bibcode:2005AREPS..33..163P. doi:10.1146/annurev.earth.33.092203.122552.
  23. ^ Leutbecher, M.; Palmer, T. N. (2008-03-20). "Ensemble forecasting". Journal of Computational Physics. Predicting weather, climate and extreme events. 227 (7): 3515–3539. Bibcode:2008JCoPh.227.3515L. doi:10.1016/j.jcp.2007.02.014.
  24. ^ Gneiting, Tilmann; Balabdaoui, Fadoua; Raftery, Adrian E. (2007-04-01). "Probabilistic forecasts, calibration and sharpness". Journal of the Royal Statistical Society, Series B. 69 (2): 243–268. CiteSeerX 10.1.1.142.9002. doi:10.1111/j.1467-9868.2007.00587.x.
  25. ^ Jewson, S; Brix, A; Ziehmann, C (2004). "A new parametric model for the assessment and calibration of medium‐range ensemble temperature forecasts". Atmospheric Science Letters. 5 (5): 96–102. arXiv:physics/0308057. Bibcode:2004AtScL...5...96J. doi:10.1002/asl.69. S2CID 118358858.
  26. ^ Jewson, S; Ziehmann, C (2004). "Using ensemble forecasts to predict the size of forecast changes, with application to weather swap value at risk". Atmospheric Science Letters. 4 (1–4): 15–27. doi:10.1016/S1530-261X(03)00003-3.

추가 정보

외부 링크