플랫 모듈
Flat module대수학에서 링 R 위에 있는 플랫 모듈은 R-모듈 M으로 텐서 제품을 R 위에 가져가면 정확한 시퀀스가 보존되는 R-모듈 M이다.원래 순서가 정확한 경우에만 텐서 제품을 시퀀스로 가져가면 모듈이 충실하게 평탄하다.
평탄도는 장 피에르 세레(1956)가 자신의 논문 제오메트리 알제브리크 외 제오메트리 애널리티크에서 소개한 것이다.평면 형태론을 참조하십시오.
정의
다음 조건이 충족되면 링 R 위의 모듈 M은 평평하다: 의 모든 주입 선형 지도 : K→ {\ L에 대해 지도
또한 주입식이며, 여기서 R 은 ) {\ m에 유도된 맵이다
이 정의를 위해서는 주사 을(를) R에 정밀하게 생성된 이상을 포함하도록 제한하기에 충분하다.
Equivalently, an R-module M is flat if the tensor product with M is an exact functor; that is if, for every short exact sequence of R-modules the sequence 도 정확하다. (텐서 제품은 정확한 functor이므로 이 정의는 동일하다.)
이러한 정의는 R이 비확정 고리인 경우에도 적용되며, M은 좌측 R모듈인 경우에도 적용된다. 이 경우 K, L, J는 우측 R모듈이어야 하며 텐서 제품은 일반적으로 R모듈이 아니라 아벨 그룹만 해당된다.
특성화
평탄도 다음과 같은 등가조건으로 특징지어질 수 있는데, 이는 M의 R-선형관계는 R의 선형관계에서 비롯된다는 것을 의미한다.R-모듈 M은 모든 선형 관계에 대해 평탄한 경우만 해당된다.
∈ 및 M y M{\ 그리고[1] 같은 요소가 .
모듈의 n 요소를 정의하는 것과 같으며, 부터 이 모듈까지의 선형 지도가 R의 표준 기준을 n 요소에 매핑한다.이를 통해 다음과 같이 동음이의어적 관점에서 이전의 성격을 다시 쓸 수 있다.
R-모듈 M은 다음 조건이 유지되는 경우에만 평탄하다 F → , where is a finitely generated free R-module, and for every finitely generated R-submodule of the map factors through a map g to a free R-module such that
다른 모듈 속성과의 관계
평탄도는 자유형, 투영형 또는 비틀림 없는 것과 같은 다양한 다른 모듈 속성과 관련이 있다.특히 모든 평면 모듈은 비틀림 없이, 모든 투영 모듈은 평평하며, 모든 자유 모듈은 투영적이다.
평평하고 투영적이지 않은 모듈들이 미세하게 생성된다.그러나 정밀하게 생성된 모듈은 가장 일반적으로 고려되는 링 위에 모두 투영된다.
이것은 다음 그래픽에 부분적으로 요약되어 있다.
비틀림 없는 모듈
모든 플랫 모듈은 비틀림이 없다.이것은 m = 1을 취함으로써 관계의 측면에서 위의 특성화에서 비롯된다.
그 역은 정수를 차지하며, 더 일반적으로 주요한 이상적인 영역과 디데킨드 링을 지배한다.
모든 토션 없는 모듈이 평평한 통합 도메인을 Prüfer 도메인이라고 한다.
자유형 및 투영형 모듈
모듈 M은 자유 모듈 G와 두 개의 선형 맵 가 있는 경우에만 투영된다 → G 및 : G→ M = i . i { 특히 자유 모듈은 투영적이다(take = M 및 i = i = i=p=\}).
모든 투영 모듈은 평평하다.는 g= f f및 = . }을(를) 취함으로써 선형 지도 측면에서 평면성과 투영성의 위의 특성화로부터 증명할 수 있다
반대로 미세하게 생성된 평면 모듈은 보통 역대수와 대수 기하학에서 만족하는 가벼운 조건에서 투영된다.이것은 평탄도의 개념을 정밀하게 생성되지 않은 모듈들에 주로 유용하게 만든다.
정밀하게 표시된 모듈(정밀하게 생성된 하위 모듈에서 자유 모듈을 정밀하게 생성한 비율)은 항상 투영적이다.이는 상기의 평탄도 특성화에서 굴절성과 = 를 선형 지도 관점에서 취함으로써 증명할 수 있다. g() = 은 선형 지도 : → G = 따라서 i = = f는 굴절적이므로 i= M은 투영적이다.
노메트리안 링 위에, 모든 미세하게 생성된 플랫 모듈은 투영적이다. 왜냐하면 미세하게 생성된 모든 모듈은 미세하게 표시되기 때문이다.비록 노에테리아인이 아니더라도, 같은 결과가 통합 도메인 상에서 사실이다.[2]
지역 링에서 미세하게 생성된 모든 플랫 모듈은 무료다.
투사성이 없는 정밀하게 생성된 평면 모듈은 다음과 같이 제작할 수 있다. = N {\F^{\N}}}}}}}}은(는) 고정 필드 F에 속하는 무한 시퀀스의 집합이다.그것은 덧셈과 곱셈이 성분에 따라 정의되는 정류 링이다.이 링은 절대적으로 평평하다(즉, 모든 모듈이 평평하다).필자가 한정된 수의 0이 아닌 항을 가진 시퀀스의 이상인 모듈 / , 은 따라서 평평하고 정밀하게 생성되지만(발생기 한 개만) 투영되지는 않는다.
비예시
- 만약 내가 노메테리아 정류 링 R에서 이상적이라면,/ 은(이것은 사각형과 동일한 원소)에 의해 생성되는 경우를 제외하고 플랫 모듈이 아니다.특히 R이 통합 도메인인 경우, I 이(가) R과 같거나 0 이상일 경우에만 이(가) 평탄하다.
- 일체형 영역에 걸쳐 플랫 모듈은 비틀림이 없다.따라서 0이 아닌 비틀림 요소를 포함하는 모듈은 평평하지 않다.In particular and all fields of positive characteristics are non-flat -modules, where is the ring of integers, and is the field of the rational numbers.
직접 합계, 한도 및 제품
모듈의 직접 합계 i 은 각 이 평평한 경우에만 평탄하다.
플랫의 직접적인 한계는 평평하다.특히 무료 모듈의 직접적인 한계는 평탄하다.반대로 모든 플랫 모듈은 정밀하게 생성된 자유 모듈의 직접적인 한계로 기록될 수 있다.[3]
플랫 모듈의 직접 제품은 일반적으로 플랫이 필요하지 않다.사실, R 링이 주어진 경우, R이 일관성 있는 링인 경우에만(즉, 미세하게 생성된 모든 이상은 정밀하게 제시된다) 플랫 R-모듈의 모든 직접 제품은 평평하다.[4]
플랫 링 익스텐션
S가 동형성에 유도된 모듈 구조에 대한 평면 R-모듈이라면 링 동형성R → R S은 평탄하다.예를 들어, 모든 링 R에 대해 다항식 링 R[t]은 R 위에 평평하다.
정류 R 의 모든 곱셈 하위 집합 에 대해국산화 S- 은(예외적인 경우에만 투영됨) R 위에 평평하다.예를 들어 은(는) 평탄하고 . 에 대해 투영되지 않음
이(가) 노메테리아 정류자 R, 의 이상이라면 에 대한 R 의 완료 ^ {R은 하다.[5] {\I}이가 A.}의 제이콥슨 레디컬에 포함되어 있는 경우에만 충실하게 평탄하다(자리스키 링도 참조).[6]
현지화
이 절에서 R은 정류 링을 가리킨다. 이(가) R의 주요 이상이라면 p 의 국산화(localization)는 평소와 을 인덱스로 표시한다.That is, and, if M is an R-module,
R-모듈 M이 평탄한 경우, M {은(는) 모든 이상 . -module이다.
Conversely, if is a flat -module for every maximal ideal , then M is a flat R-module (and is a flat -모든 주요 p {\에 대해 사용 가능.
이러한 성질은 국소 고리의 경우 평탄성 문제를 줄여주기 때문에 역학대수에 있어서 기본적인 것이다.그들은 종종 평탄함이 지역 재산이라고 말함으로써 표현된다.
평면적인 체계 형태론
f : → {\ f Y 체계의 모피즘은 국부적으로 유도된 지도가 울리면 평평한 형태론이다.
X의 어떤 점 X에 대한 평평한 고리 동형상이다.따라서 평면(또는 충실하게 평면) 고리 동형성의 특성은 대수 기하학 기하학에서 자연스럽게 평면 형태론의 기하학적 특성으로 확장된다.예를 들어, = [ , x, /( - t )의 이전 예를 고려해 보십시오 [ R 에 따라 평면 형태론이 결정된다.
각 (기하학) 섬유 - ( t) 은 방정식 = . 의 곡선이다 또한 평평한 변성 및 일반 원뿔에 대한 변형을 참조하십시오.
S= [ x ,…, x 은(는) 비저다이저(nonzerodivisor)인 노메트리안 링 f S에 대한 다항식 링이다.그런 다음 / 이가) 원시인 경우에만 위에 평탄하다(계수가 단위 이상 생성).[7]예를 들어 [ , , / (x - t), 가 있는데[8]pg 3, 이 은 C 에 대해 평탄(무료도)하다(기하 참조).이러한 평면 확장은 자유롭지 않고 국산화에서 비롯되지 않는 평면 모듈의 예를 산출하는 데 사용될 수 있다.
충실한 평탄도
원래 순서가 정확한 경우에만 텐서 제품을 시퀀스로 가져가면 모듈이 충실하게 평탄하다.이 개념은 필요 없는 교환 링 위에 있는 모듈에 대해 정의되지만, 주로 교환 알제브라에 사용된다.그러므로, 비록 어떤 결과가 비약속 링 위에 있는 모듈의 경우에 일반화될 수 있다 하더라도, 이 경우는 여기서 고려되는 유일한 경우다.
절에서 : R→ 은(는 -algebra 및 -module의 구조를 하는 정류 링의 동형성이다 이(가) -module 플랫(또는 충실하게 플랫)인 경우, 일반적으로 이가) ,{\보다 플랫(또는 완전하게 플랫)이라고 있다.
이(가) , 위에 평평한 경우 다음 조건이 동등하다.
- 은(는) 충실하게 평탄하다.
- 의 각 최대 m 에 대해 1개는 을(를) 가지고 있다.
- 이(가) 0이 아닌 -module이면 M⊗ ≠
- For every prime ideal of there is a prime ideal of such that 다시 말해, 스펙트럼상f operatorname {S에 의해 유도된 f :() → (R은 억측 대상이다.
- is injective, and is a pure subring of that is, is injective for every -module .[9]
두 번째 조건은 지역 고리의 평평한 국소 동형성이 충실하게 평평하다는 것을 의미한다.= 라는 마지막 조건부터 따르게 된다. 의 모든 이상 에 대한 테이크 = / 특히 이(가) 노메트리안 고리라면 도 노메트리안이다.
The last but one condition can be stated in the following strengthened form: is submersive, which means that the Zariski topology of is the quotient topology of that of ) 이는 충실히 평평한 준 컴팩트 형태의 체계들이 이 속성을 가지고 있다는 사실에 대한 특수한 경우다.[10]플랫 모피즘# 플랫 모피즘의 속성을 참조하십시오.
예
- 이(가) 0이 아닌 자유 R-모듈인 링 동형성 → 은(는) 충실하게 평탄하다.예를 들면 다음과 같다.
- Let The direct product of the localizations at the is faithfully flat over if and only if 의 단위 이상 생성(즉, 이(가) 의 선형 조합인 경우).[11]
- {\ R}의R p displaystyle 의 모든 주요 이상에 대한 직접적인 합은 완전히 평평한 모듈이며, 이는 완전히 많은 기본 이상이 있는 경우를 제외하고는 대수학이 아니다.
마지막 두 예는 역학 대수학 및 대수 기하학에서 국산화 사용이 광범위하게 사용된 배후에 있다.
- 주어진 링 동형상 : → , 아미츠르 콤플렉스라고 불리는 관련 콤플렉스가 있다.[12]여기서 동시경계 연산자 은 각 지점에 1을 삽입하여 얻은 맵의 교대 합이다. 예: = - \delta \delta (그로텐디크) 이 콤플렉스는 f 이(가) 충실하게 평탄하다면 정확하다.
충실하게 평평한 국소 동음이의어
여기 불필요하게 평평한 동형성에 대한 충실하게 평평한 동형성의 한 가지 특성이 있다.Given an injective local homomorphism such that is an -primary ideal, the homomorphism is faithfully flat ifand only if the theorem of transition holds for it; that is, for each -primary ideal of , [13]
Tor functor를 이용한 동질적 특성화
평탄도는 텐서 제품의 왼쪽 파생 펑터인 Tor functors를 사용하여 표현할 수도 있다.좌측 R-모듈 M은 다음과 같은 경우에만 평탄하다.
- (, )= n } 1 및 all right R-modules X).[14]
사실, 첫 번째 토르 용어가 사라졌는지, 즉 M은 만약의 경우에 한해서만 평평하다는 것을 확인하는 것으로 충분하다.
모든 R-모듈 N의 경우 또는 제한적으로 N= R/ 및 R 이(가) 정밀하게 생성된 이상일 경우.
Tor functor의 긴 정확한 시퀀스를 사용하여, 사람들은 짧은 정확한 시퀀스에 대한 사실을 쉽게 증명할 수 있다.
A와 C가 평평하다면 B도 평평하다.또한 B와 C가 평평하다면 A도 그렇다.A와 B가 평평하다면, C는 일반적으로 평평할 필요가 없다.그러나 A가 B에서 순수하고 B가 평평하면 A와 C가 평평하다.
평탄한 해상도
모듈 M의 평탄한 분해능은 폼의 분해능이다.
여기서 F는i 모두 평평한 모듈이다.자유롭거나 투영적인 해상도는 반드시 평탄한 해상도다.평평한 해상도는 Tor functor를 계산하는 데 사용될 수 있다.
들은 한정된 평평한 결의안에 대한 길이는 첫번째 첨자 n 같은 Fn{\displaystyle F_{n}}와 F나는 초기 조향 순간 0{\displaystyle F_{나는}=0}에 나는입니다. 조금, n{\displaystyle i>, n}. 모듈 M들은 한정된 평평한 해상도, M의 모든 유한한 평평한 결심 사이에 그것의 평평한 치수용이라고 불리는 최소한의 길이 입장할 수 있다.15]와 드명시된 fd(M). 만일 M이 유한한 평면 분해능을 인정하지 않는다면 관습에 의해 평면 치수는 무한하다고 한다.예를 들어 fd(M) = 0과 같은 모듈 M을 생각해 보자. 이 상황에서 시퀀스 0 → F → M0 → 0의 정확도는 중앙의 화살표가 이형성임을 나타내며, 따라서 M 자체는 평탄하다.[16]
모듈 이론의 일부 영역에서, 평탄한 해상도는 각 지도가 지도 커널의 오른쪽을 평탄한 사전 커버라는 추가 요건을 충족해야 한다.투사적 해결책의 경우, 이 조건은 거의 보이지 않는다: 투사적 사전 커버는 투사적 모듈에서 나오는 단순한 경구체일 뿐이다.이 아이디어들은 아우슬란더의 근사치 작품에서 영감을 얻은 것이다.이러한 생각들은 또한 최소의 투영적 해상도라는 보다 일반적인 개념에서 익숙하다. 여기서 각 지도는 지도에서 오른쪽으로의 커널의 투영적 표지가 되어야 한다.그러나 일반적으로 투사형 커버가 존재할 필요는 없으므로 최소 투사형 해상도는 정수처럼 링에 제한적으로 사용될 뿐이다.
플랫 커버
모듈에 대한 투영 커버가 항상 존재하는 것은 아니지만, 일반 링의 경우, 모든 모듈 M은 평면 모듈 F의 경구적 이미지일 것이고, 즉 모든 모듈 M은 평면 모듈에서 F를 통한 M 인자에 이르는 모든 맵이 될 것이며, M을 통한 F의 내형성은 자동포착이라고 추측되었다.이 평평한 덮개 추정은 (Enochs 1981, p 196) 에 명시적으로 언급되었다:(그 추측이 사실로 밝혀지고, 긍정적으로 해결되었으며, L. Bican, R. E. E.에 의해 동시에 증명되었다.에녹스.[17]이것은 P의 중요한 기여가 선행되었다.에클로프, J. 트릴리파지, J. 쉬.
모든 링에 걸쳐 모든 모듈에 대해 플랫 커버가 존재하므로, 여러 상황에서 최소의 플랫 해상도는 최소의 투영 분해능을 대신할 수 있다.투사적 분해능에서 평면 분해능의 이탈 측정을 상대적 호몰로지 대수라고 하며, (MacLane 1963) (과 같은 평면 분해능에 초점을 맞춘 더 최근의 작품에서는 (Enochs & Jenda 2000)과 같은 평면 분해능에 초점을 맞추고 있다.
건설수학에서
평면 모듈은 전도성 모듈이 덜 유용한 건설적 수학에서 중요성이 증가했다.예를 들어, 모든 자유 모듈이 투영적이라는 것은 선택의 완전한 공리와 동등하기 때문에, 건설적으로 증명되더라도, 투영 모듈에 대한 이론이 반드시 자유 모듈에 적용되는 것은 아니다.대조적으로, 무료 모듈이 평평하다는 것을 증명하기 위해 어떤 선택도 필요하지 않기 때문에, 플랫 모듈에 대한 이론은 여전히 적용될 수 있다.[18]
참고 항목
- 일반 평탄도
- 평면 형태론
- 폰 노이만 일반 링 – 모든 모듈이 평평한 링.
- 보통 플랫 링
참조
- ^ 부르바키, 장 I, § 2. 발의안 제13호, 코롤라리 1호.
- ^ Cartier, Pierre (1958). "Questions de rationalité des diviseurs en géométrie algébrique". Bulletin de la Société Mathématique de France (in French). Lemme 5, page 249. 86: 177–251. doi:10.24033/bsmf.1503.
{{cite journal}}: CS1 maint : 위치(링크) - ^ (Lazard 1969)
- ^ (1960년 구매)
- ^ 마츠무라 1970, 정리 55의 코롤라리 1 페이지 170
- ^ 마츠무라 1970, 정리 56
- ^ 아이젠버드, 연습 6.4. (
- ^ Artin. "Deformation theory" (PDF). Archived (PDF) from the original on 28 Oct 2020.
- ^ 증명: : → S 는 충실하게 평탄하다.For an R-module the map exhibits as a pure subring and so 는 주입식이다.따라서 → 는 주입식이다.반대로 ≠ 0이가) R R에 있는 모듈이라면, ≠ M . M
- ^ SGA 1, Exposé VIII, Corollay 4.3. (
- ^ Artin, 연습 (3) 발의안 제3.5.2항 이후.
- ^ "Amitsur Complex". ncatlab.org.
- ^ 마츠무라 1986, 8장 22.1 운동.
- ^ 마찬가지로 오른쪽 R-모듈 M은 모든 1 1및 모든 왼쪽 R-module X에 (, )= 0 인 경우에만 평탄하다.
- ^ 램 1999, 페이지 183.
- ^ 평평한 모듈에 대한 이형성 모듈은 물론 평평하다.
- ^ 비칸, 엘 바시르 & 에녹스 2001.
- ^ 리치맨 1997.
- Artin, Michael (1999). "Noncommutative Rings" (PDF).
- Bican, L.; El Bashir, R.; Enochs, E. (2001), "All modules have flat covers", Bull. London Math. Soc., 33 (4): 385–390, doi:10.1017/S0024609301008104, ISSN 0024-6093, MR 1832549
- Bourbaki, Nicolas. Commutative Algebra.
- Chase, Stephen U. (1960), "Direct products of modules", Transactions of the American Mathematical Society, 97 (3): 457–473, doi:10.2307/1993382, JSTOR 1993382, MR 0120260
- Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, vol. 150, Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4612-5350-1, ISBN 978-0-387-94268-1, MR 1322960
- Enochs, Edgar E. (1981), "Injective and flat covers, envelopes and resolvents", Israel Journal of Mathematics, 39 (3): 189–209, doi:10.1007/BF02760849, ISSN 0021-2172, MR 0636889, S2CID 120567780
- Enochs, Edgar E.; Jenda, Overtoun M. G. (2000), Relative homological algebra, de Gruyter Expositions in Mathematics, vol. 30, Berlin: Walter de Gruyter & Co., doi:10.1515/9783110803662, ISBN 978-3-11-016633-0, MR 1753146
- Kunz, Ernst (1969), "Characterizations of regular local rings of characteristic p", American Journal of Mathematics, 91 (3): 772–784, doi:10.2307/2373351, JSTOR 2373351, MR 0252389
- Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, vol. 189, Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4612-0525-8, ISBN 978-0-387-98428-5, MR 1653294
- Lazard, Daniel (1969), "Autour de la platitude", Bulletin de la Société Mathématique de France, 97: 81–128, doi:10.24033/bsmf.1675
- Mac Lane, Saunders (1963), Homology, Die Grundlehren der mathematischen Wissenschaften, Bd. 114, Boston, MA: Academic Press, MR 0156879
- Matsumura, Hideyuki (1970), Commutative algebra
- Matsumura, Hideyuki (1986). Commutative ring theory. Cambridge Studies in Advanced Mathematics. Vol. 8. Cambridge University Press. ISBN 0-521-36764-6. MR 0879273. Zbl 0603.13001.
- Mumford, David, The red book of varieties and schemes
- Northcott, D. G. (1984), Multilinear algebra, Cambridge University Press, ISBN 978-0-521-26269-9 - 33페이지
- Richman, Fred (1997), "Flat dimension, constructivity, and the Hilbert syzygy theorem", New Zealand Journal of Mathematics, 26 (2): 263–273, ISSN 1171-6096, MR 1601663
- Serre, Jean-Pierre (1956), "Géométrie algébrique et géométrie analytique", Annales de l'Institut Fourier, 6: 1–42, doi:10.5802/aif.59, ISSN 0373-0956, MR 0082175




















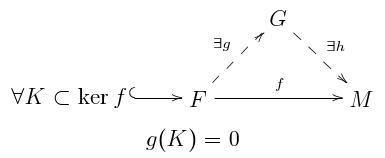









 선형 지도
선형 지도 

 투영적이다.
투영적이다. 


 같거나 0
같거나 0



 평평한 경우에만 평탄하다.
평평한 경우에만 평탄하다.  .예를 들어, 모든 링
.예를 들어, 모든 링  모든
모든 
 (예외적인 경우에만
(예외적인 경우에만 


 (가)
(가) 







 모피즘은 국부적으로 유도된 지도가 울리면
모피즘은 국부적으로 유도된 지도가 울리면 
![{\displaystyle R=\mathbb {C} [t,x,y]/(xy-t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f79d023d7cdf8e4bdb742ecb2b9c7d7903d1060)
![{\displaystyle \mathbb {C} [t]\hookrightarrow R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d9fd115e5bf386bb4e0c69d5aeab83cd38d876e)
![{\displaystyle \pi :\operatorname {Spec} (R)\to \operatorname {Spec} (\mathbb {C} [t]).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b076bd46405a1a8f543594234291686a55b5529)


 노메트리안 링
노메트리안 링 ![{\displaystyle S=R[x_{1},\dots ,x_{r}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6e65c3af29ebe78c3d4381fea16f5a939b419e8)

![{\displaystyle \mathbb {C} [t,x,y]/(xy-t),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d5fd7b6e89cf6b9acfc62c69b2f3d82d1ce8785)
![{\mathbb {C}}[t]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d83161b277d877a8dd4ad77c9884af86de11c2e4)
 (는
(는 (가) 0이 아닌
(가) 0이 아닌 





 대한
대한 



![{\displaystyle p\in R[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4830e9e21e96da6790f048b35d448d9884d4409e) (가)
(가) ![{\displaystyle R\hookrightarrow R[t]/\langle p\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e2cfd7bc65824943c99fb8e554266653ca9851)

![{\displaystyle \textstyle \prod _{i}R[t_{i}^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff8f38a6177cb947ef6015141f4d1cbc6270ac8f)


 (가)
(가) 
















 충실하게 평탄하다.For an
충실하게 평탄하다.For an