정확한 순서

정확한 순서는 하나의 형태론의 이미지가 다음 것의 알맹이와 같도록 물체들 사이의 형태화 순서(예를 들어 그룹, 반지, 모듈, 그리고 보다 일반적으로 아벨의 범주의 물체)null

정의

집단 이론의 맥락에서, 순서는

${\displaystyle G_{0}\;{\xrightarrow {\ f_{1}\}}\;G_{1}\;{\xrightarrow {\ f_{2}\}}}\;G_{2}\;{\xrightarrow {\f_{3}\}\}\\cdots \;{\xrightarrow {\f_{n}\}}\;;;;G_{n}}$

그룹 및 그룹 동형성의 정확한 값은 ${\displaystyle \mathrm{im}{display}_{}}$$($ i ) = $ker$${\displaystyle {}_{}}$${($${\displaystyle f_{}}$i${\displaystyle {}_{}}$+ ${\displaystyle 1_{}}$) ${\displaystyle \operatorname {im}(f_{i})$이라고 한다.$=\ker(f_{i+1})}$. ${\displaystyle {Gi}_{}}$ ${\$에서 1$$ i< ${\displaystyle 1\leq$ i 즉, 각 동형성의 이미지가 다음 낟알과 같으면 시퀀스가 정확한 것으로 불린다.null

집단과 동형성의 순서는 유한하거나 무한할 수 있다.null

다른 대수 구조에 대해서도 유사한 정의를 내릴 수 있다.예를 들어, 벡터 공간과 선형 지도 또는 모듈과 모듈 동형성의 정확한 순서를 가질 수 있다.보다 일반적으로, 정확한 수열의 개념은 커널과 코커넬이 있는 어떤 범주에서도, 특히 널리 사용되는 아벨리아 범주에서는 더욱 이치에 맞는다.null

단순 사례

정의를 이해하기 위해서는 순서가 유한하고 사소한 그룹으로 시작하거나 끝나는 비교적 단순한 경우를 고려하는 것이 도움이 된다.전통적으로 이것은 단일 식별 요소와 함께 0(가법적 표기법, 보통 그룹이 아벨일 때 추가 표기법)으로 표시되거나 1(승법 표기법)으로 표시된다.null

• 순서 0 → A → B를 고려한다.맨 왼쪽 지도의 이미지는 0이다.따라서 가장 오른쪽 지도(A에서 B까지)가 커널 {0}을(를) 갖는 경우에만, 즉 그 지도가 단형성(내성적 또는 일대일)인 경우에만 시퀀스가 정확하다.
• 이중 시퀀스 B → C → 0을 고려한다.가장 오른쪽 맵의 커널은 C이다.따라서 가장 왼쪽 지도 이미지(B에서 C까지)가 모두 C일 경우에만, 즉 그 지도가 경구형(추상형)일 경우에만 시퀀스가 정확하다.
• 따라서 X에서 Y까지의 지도가 단형성과 경형성(즉, 이형성), 즉 X에서 Y까지의 이형성인 경우에 한하여 0 → X → Y → 0의 순서가 정확하다.

짧은정확한순서

중요한 것은 폼의 정확한 순서인 짧은 정확한 순서다.

${\displaystyle 0\to A\xrightarrow {f}B\xrightarrow {g}C\to 0.}$

위에서 확립한 바와 같이, 그러한 짧은 정확한 수열에서 f는 단동형이고 g는 경동형이다.더욱이 f의 이미지는 g의 커널과 같다.A를 A를 B에 내장한 B의 하위 개체로 생각하고, C를 해당 인자 개체(또는 지수)인 B/A로 생각하면 g가 이형성을 유도하는 것이 도움이 된다.

${\displaystyle C\cong B/\operatorname {im}(f)}$

짧은 정확한 순서는

${\displaystyle 0\to A\xrightarrow {f}B\xrightarrow {g}C\to 0\,}$

구성 g ∘ h가 C의 ID 맵인 것처럼 동형상 h : C → B가 존재하는 경우 split이라고 한다.이들이 아벨 그룹이라면, B는 A와 C의 직접 합에 이형성이라는 것이 뒤따른다.

$B\conditionstyle B\cong.}$

긴정확열

일반적인 정확한 순서는 때때로 짧은 정확한 순서의 특수한 경우와는 구별하기 위해 긴 정확 시퀀스라고 불린다.^[1]null

긴 정확한 순서는 다음과 같은 의미에서 짧은 정확한 순서의 계열과 같다: 긴 순서가 주어진다.

${\displaystyle A_{0}\;\xrightarrow {\ f_{1}\ } \;A_{1}\;\xrightarrow {\ f_{2}\ } \;A_{2}\;\xrightarrow {\ f_{3}\ } \;\cdots \;\xrightarrow {\ f_{n}\ } \;A_{n},}$ (1)

n ≥ 2로, 우리는 그것을 짧은 시퀀스로 나눌 수 있다.

${\displaystyle {\begin{aligned}0\rightarrow K_{1}\rightarrow {}&A_{1}\rightarrow K_{2}\rightarrow 0,\\0\rightarrow K_{2}\rightarrow {}&A_{2}\rightarrow K_{3}\rightarrow 0,\\&\ \,\vdots \\0\rightarrow K_{n-1}\rightarrow {}&A_{n-1}\rightarrow K_{n}\rightarrow 0,\\\end{aligned}}}$ (2)

여기서 ${\displaystyle {Ki}_{}}$= ${\displaystyle \mathrm{im}}$ ${\displaystyle }$ ${\displaystyle (f_{}}$ i ${\displaystyle {}_{}}$ ${\displaystyle K_{i}=\operatorname {im}(f_{i})$은 $모든{\displaystyle }$ i ${\displaystyle i}$에 대해$$ 정확하다$.$ 시공에 따르면 시퀀스(2)는 Ki ${\$의 정확도에 관계없다.또한 (1)은 (2)가 모두 짧은 정확한 시퀀스인 경우에만 긴 정확한 시퀀스다.null

예

정수모듈로2번길

다음 아벨 그룹 순서를 고려하십시오.

${\displaystyle \mathbf {Z} \mathrel {\overset {2\times }{\\\hookrightarrow }}} \mathbf {Z} \mathbf {Z}}}}$

첫 번째 동형동식은 정수 Z의 각 요소 i를 Z의 요소 2i에 매핑한다.두 번째 동형성은 Z의 각 요소 i를 지수 그룹의 요소 j에 매핑한다. 즉, j = i mod 2이다.여기서 후크 화살표 $↪{\displaystyle \hookrightarrow}$는 Z에서 Z로 2×하는 지도가 단형임을 나타내며, 2-head 화살표 $\twoheadrightarrow {\displaystyle }${\$displaystyle \twoheadrightarrow}}$는 인식형(지도모드 2)을 나타낸다$$.단형주의 이미지 2Z가 경동주의 알맹이이기 때문에 이것은 정확한 배열이다.본질적으로 "동일한" 순서도 다음과 같이 쓸 수 있다.

${\displaystyle 2\mathbf {Z} \mathrel {\,\hookrightarrow {Z} \mathbf {Z} \twoheadrightarrow \mathbf {Z} /2\mathbf {Z}}}}}$

이 경우 단형성은 2n ↦ 2n이며, 비록 신분함수처럼 보이지만 홀수가 2Z에 속하지 않기 때문에 (즉, 경형주의가 아니다) 위에 있지 않다.그러나 이 단모형을 통한 2Z의 이미지는 이전 순서에 사용된 Z ~ n ↦ 2n의 이미지와 정확히 동일한 부분집합이다.이 후자의 순서는 첫 번째 물체의 구체적인 성질이 이전 것과 다르다. 2Z는 비록 두 개 집단이 이형이지만 Z와 같지 않기 때문이다.null

첫 번째 시퀀스는 단형주의와 경구성을 위한 특별한 기호를 사용하지 않고 다음과 같이 쓰여질 수 있다.

${\displaystyle 0\to \mathbf {Z} \mathrel {\overset {2\times }{\longrightarrow }} \mathbf {Z} \mathbf {Z} \to 0}$

여기서 0은 사소한 그룹을 나타내며, Z에서 Z까지의 맵은 2 곱하기, Z에서 인자 그룹 Z/2Z까지의 맵은 정수 modulo 2를 줄임으로써 주어진다.이것은 정말로 정확한 순서다.

• 맵 0 → Z의 이미지는 {0}이고 곱하기 2의 커널도 {0}이므로 첫 번째 Z에서 순서가 정확하다.
• 곱하기 2의 이미지는 2Z이고, 모듈로 2를 줄이는 커널도 2Z이므로 두 번째 Z에서 순서가 정확하다.
• 환원모듈로2의 이미지는 Z/2Z이고, 제로맵의 커널도 Z/2Z이기 때문에 Z/2Z 위치에서 순서가 정확하다.

첫 번째와 세 번째 시퀀스는 Z의 무한한 특성 때문에 다소 특별한 경우다.유한집단이 그 자체의 적절한 하위집단으로 포섭(즉, 단동형성에 의해)에 의해 지도화되는 것은 불가능하다.그 대신 첫 번째 이형성 정리에서 나오는 순서는 다음과 같다.

$1 to N\to G\to G/N\to 1}$

유한한 그룹에 대한 정확한 시퀀스의 보다 구체적인 예로서,

${\displaystyle 1\to C_{n}\to D_{2n}\to C_{2}\to 1}$

여기서 $C{\displaystyle {}_{}}$ ${\displaystyle n_{}}$ ${\$는 순서 n의 주기적 그룹이고 $D{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{2n}}_{}}$ ${\$은 순서$$ 2n의 디헤드 그룹으로, 비아벨리안 그룹이다.null

모듈 교차점 및 합

나와 J는 반지 R의 두 개의 이상이 되게 하라.그러면

$0\displaystyle 0\to I\cap J\to I\oplus J\to I+J\to 0}$

is an exact sequence of R-modules, where the module homomorphism ${\displaystyle I\cap J\to I\oplus J}$ maps each element x of ${\displaystyle I\cap J}$ to the element ${\displaystyle (x,x)}$ of the direct sum ${\displaystyle I\oplus J}$, and the homomorphsim ${\displays$$Tyle I\$$oplus$ $J\to I+$$J}$의 각 $($${\displaystyle \mathrm{x<img\; alt="(x,y)"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/41cf50e4a314ca8e2c30964baa8d26e5be7a9386"\; style="vertical-align:\; -0.838ex;\; width:5.328ex;\; height:2.843ex;"\; papago-attr-id="132">}}$, ${\displaystyle y}$) ${\displaystyle \{\backslash }$$displaystyle I\oplus J}$을$(를)$ $x{\displaystyle }$-$$에 매핑한다$$$.$

이러한 동형성들은 짧은 정확한 순서를 형성하는 유사하게 정의된 동형성들의 제한이다.

$R\oplus R\oplus R\to 0}$

지수 모듈로 전달하면 또 다른 정확한 시퀀스가 생성됨

${\displaystyle 0\to R/(I\cap J)\to R/(I+J)\to 0}$

차등 지오메트리에서의 그라데이션, 컬링 및 디브

이 섹션은 위키피디아의 품질 기준을 충족시키기 위해 정리가 필요할 수 있다.구체적인 문제는 다음과 같다."우리"와 "주"를 너무 많이 사용함. 또한 이 절은 이 글의 대부분의 독자들에게 너무 기술적이다. 이 절은 문장을 이해하는 데 필요한 정의(순서의 정확성)로 축소되어야 한다. 증거와 기술적 세부사항은 이 기사에 속하지 않고 차등 기하학의 기사에 나타나야 한다. 가능한 경우 이 섹션을 개선하는 데 도움을 주십시오. (2019년 12월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

다른 예는 특히 맥스웰 방정식의 작업에 관련된 미분 기하학에서 도출될 수 있다.null

Consider the Hilbert space ${\displaystyle L^{2}}$ of scalar-valued square-integrable functions on three dimensions ${\displaystyle \left\lbrace f:\mathbb {R} ^{3}\to \mathbb {R} \right\rbrace }$. Taking the gradient of a function ${\displaystyle f\in \mathbb {H} _{1}}$ moves us toa subset of ${\displaystyle \mathbb {H} _{3}}$, the space of vector valued, still square-integrable functions on the same domain ${\displaystyle \left\lbrace f:\mathbb {R} ^{3}\to \mathbb {R} ^{3}\right\rbrace }$ — specifically, the set of such functions that represent conservative vector fields. (일반화된 스톡스의 정리는 통합성을 보존했다.)null

첫째, 이러한 모든 필드의 컬은 0이므로 0이라는 점에 유의하십시오.

${\displaystyle \chostname {grad}(\displayname {grad}f)\equiv \chbla \pairla \p)=0}$

이 모든 것에 대해서그러나 이것은 그라데이션의 이미지가 컬의 커널의 부분집합이라는 것을 증명할 뿐이다.실제로 동일한 집합임을 입증하려면 역순을 입증하십시오. 벡터 필드 $F{\displaystyle \stackrel{}{}}$→ ${\$의 컬이 0이면$$ $F{\displaystyle \stackrel{}{}}$→ ${\$이(가) 일부 스칼라 함수의 그라데이션임을$$ 증명하십시오.이는 스톡스의 정리로부터 거의 즉시 뒤따른다(보수 세력에서의 증명 참조).그라데이션의 이미지는 정확히 컬의 커널이고, 그래서 우리는 컬을 다음 ${\displaystyle {}_{}}$으로 가져갈 수 있고, H $3{\displaystyle {\mathbb{}}_{}}$ ${\$의 (다른) 부분집합으로 우리를 다시 데려갈 수 있다$.$

마찬가지로, 우리는 이 점을 주목한다.

${\displaystyle \div} \left(\dvname {v}\right)\equiv \cdot \cdla \cdla \cdla \v}{v}=0,}$

그래서 컬의 이미지는 분리의 알맹이의 부분집합이다.그 반대의견은 다음과 같다.

$일부{\displaystyle \stackrel{}{}}$${\displaystyle A}$ →${\$$displaystyle \operatorname {div}{\vec$${F$$}}$ $$= 0이($가{\displaystyle \stackrel{}{})}$ F → ${\displaystyle curl\stackrel{}{}}$ ${$A${\displaystyle \stackrel{}{}}$→ {\$vec{$F}=\$operatorname$ {$curl}{\$$vec${A$$$}}}$ 일부 A → {\$displaystystystyle {\\vec}}}}}}}}}$을(으)를 의미한다는 증거

우리는 시공으로 진행할 것이다: 벡터${\displaystyle \stackrel{}{}}필드{\displaystyle \stackrel{}{}{}_{}}$ → = ${\displaystyle F_{}}$ ${\displaystyle {}_{}\stackrel{}{}}$i${\displaystyle }$^ + ${\displaystyle {}_{}\stackrel{}{}}$ y j ${\displaystyle \stackrel{}{^}}$+ ${\displaystyle {}_{}\stackrel{}{}}$ ${\displaystyle z_{}}$ k ${\displaystyle \stackrel{}{^}}$ ${\$$F\_{\displaystyle \stackrel{}{}}$${y}{\hat{j}}+F_{z}{\k}}{\$data${$k$$}}}(으)${\displaystyle \mathrm{}\mathrm{such}}$F${\displaystyle \stackrel{}{}}$→${\displaystyle }$= 0 ${\displaystyle \nabla \cdot{\vec}=0$ 필드 A${\displaystyle \stackrel{}{}}$→ ${\$를 생성한다$$. ${\displaystyle {\begin{aigned}\nabla \time {\vec{A}&=\좌측(\partial _{y}A_{z}-\partial _{z})A_{y}\오른쪽){\hat{i}+\왼쪽(\hats _{z})A_{x}-\partial _{x}A_{z}\오른쪽){\hat {j}+\좌(\partial _{x}A_{y}-\partial _{y}-\partial _{y}A_{x}\오른쪽){\hat{k}\&=F_{x}{\hat{i}+F_{y}{\hat{j}+F_{z}{\hat {k}={\vec{F}\end}}}}$ 첫째, 위에서 ${\displaystyle \mathrm{curl}}$ ${\displaystyle (\mathrm{grad}}$ ${\displaystyle }$ f${\displaystyle }$)${\displaystyle }$= 0 ${\displaystyle \operatorname {curl}(\operatorname {grad}f)=0}$을$($를) 증명되었으므로, 컬을 $변경$하지 않고$$ 스칼라 함수의 경사를 A →${\$에 추가할 수 있다.이 게이지의 자유를 사용하여 컬을 변경하지 않고 $A{\displaystyle \stackrel{}{}}$→ ${\$의 한 구성 요소를 0으로$$ 설정할 수 있다. 따라서 z 구성 요소를 임의로 선택하면 다음과 같은 작업이 필요하다. $-\displaystyle -\display _{z}A_{y}{\hat{i}+\partial _{z}A_{x}{\hat{j}+\좌(\partial _{x}A_{y}-\partial _{y}-\partial _{y}A_{x}\오른쪽){\hat{k}=F_{x}{\hat {i}+F_{y}{\hat{j}+F_{z}{\hat{k}}}$ 그런 다음 단순히 처음 두 요소를 통합하고, 통합의 '일관적'이 여전히 통합되지 않은 어떤 변수에 의존할 수 있다는 점에 주목함으로써, 우리는 다음과 같은 사실을 알게 된다. ${\displaystyle {\reasoned}A_{x}&=\int F_{y}dz+{\vec{C_{1}}(x,y)\\\A_{y}&=-\int F_{x}dz+{\vec {C_{2}}(x,y)\ended{aigned}}}}$ 두 ${\displaystyle \stackrel{}{{통합\mathrm{}}_{}}}$ 용어 $C{\displaystyle \stackrel{}{{}_{}}}$ 1${\displaystyle \stackrel{}{{}_{}}}$→${\displaystyle }$, ${\displaystyle \stackrel{}{{C\mathrm{}}_{}}}$ 2${\displaystyle \stackrel{}{{}_{}}}$→ ${\$2}} $모두$ z가 아닌 x와 ${\displaystyle y}$에만 의존하므로, 그러면 z에도 의존하지 않는 일부$$ 함수 $f{\displaystyle (x}$, y$){\displaystyle f(x,y)$의 그라데이션도 추가할 수 있다.이로써 $우리$는 A ${\displaystyle z_{}}$ ${\$를 0으로$$ 설정했던 이전의 작업을 망치지 않고 다른 쪽을 유리한 조건 중 하나를 없앨 수 있게 되었다.$C{\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{{2\mathrm{}}_{}}}$→ ${\$ 제거하기로 선택하고 마지막$$ 구성요소를 제약조건으로 적용하면 다음과 같다. ${\displaystyle {\begin}-\partial _{x}\int F_{x}dz+\partial _{x}{\vec {C_{1}}(x,y)-\partial _{y}\int F_{y}dz&=F_{z}\\-\int \left(\partial _{x}F_{x}+\partial _{y})F_{y}\오른쪽)dz+\partial _{x}{\vec {C_{1}}(x,y)&=F_{z}\end{aigned}}}}}$ ${\displaystyle 가정}$으로 ${\displaystyle \mathrm{div}\stackrel{}{\to }}$ ${\displaystyle F_{}}$ → =${\displaystyle {\mathrm{}}_{}}$ x ${\displaystyle {}_{}{}_{}}$ +${\displaystyle {}_{}{\mathrm{}}_{}}$ ${\displaystyle y_{}}$ ${\displaystyle y_{}}$ +${\displaystyle {}_{}{\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$ =$$ ${\displaystyle \operatorname$ {$div} {\vec{F}=\partial _{x}+\partial _{y}$$F_{y}+\partial _{z}F_{z}=0}$등 ${\displaystyle \int \partial _{z}F_{z}dz+\partial _{x}{\vec {C_{1}}(x,y)=F_{z}}$ 미적분학의 근본적인 정리는 위의 첫 번째 항이 정확하게 F ${\displaystyle z_{}}$ ${\$와 z의 상수를 더해야 하기 때문에, 위의 방정식 시스템에 대한 해법이 존재할 것을 보장한다.null

따라서 컬의 이미지가 정확히 발산성의 알맹이라는 것을 증명하고, 이 형태론은 차례로 $우리$를 ${\displaystyle {L\mathrm{}}^{}}$ 2 ${\$ L$^{2}}$로부터 시작된 공간으로 데려다 준다$.$ 정의적으로 우리는 통합 가능한 기능의 공간에 착륙했기 때문에, 그러한 기능은 벡터를 생산하기 위해 (적어도 정식으로) 통합될 수 있다.발산하는 영역은 그 기능이다. 즉, 발산 ${\displaystyle {이미지}^{}}$의 전체는 L 2 {\$displaystyle L^{2}}$이고$,$ 우리는 우리의 순서를 완성할 수 있다$.$

${\displaystyle 0\to L^{2}\mathrel {\xrightarrow {\operatorname {grad} } } \mathbb {H} _{3}\mathrel {\xrightarrow {\operatorname {curl} } } \mathbb {H} _{3}\mathrel {\xrightarrow {\operatorname {div} } } L^{2}\to 0}$

동등하게, 우리는 역방향으로 추론할 수 있었다: 단순하게 연결된 공간에서, 컬이 없는 벡터 필드(컬의 커널에 있는 필드)는 항상 스칼라 함수의 구배(그러므로 그라데이션의 이미지에 있음)로 쓸 수 있다.마찬가지로, 비분산 장은 다른 필드의 컬로 쓸 수 있다.^[2] (이 방향으로의 합리화는 3차원 공간이 토폴로지적으로 하찮은 것이라는 사실을 이용한다.)null

이 짧은 정확한 순서는 또한 무수력 벡터 미적분학에 의존하지 않는 헬름홀츠 분해의 유효성에 대한 훨씬 더 짧은 증거를 허용한다.반복성을 고려하십시오.

${\displaystyle 0\to L^{2}\mathrel {\xrightarrow {\operatorname {grad}} \mathb {H} _{3}\mathrow {\xrightarrow {\opername {curl} } \operatorname {im}(\operatorname {curl})\curl})\operatorname})\curl} to 0.}에서 0.}.}.}.}.}.}$

Since the divergence of the gradient is the Laplacian, and since the Hilbert space of square-integrable functions can be spanned by the eigenfunctions of the Laplacian, we already see that some inverse mapping ${\displaystyle \nabla ^{-1}:\mathbb {H} _{3}\to L^{2}}$ must exist.그러한 역성을 명시적으로 구성하기 위해서는 벡터 라플라시안(Vector Laplacian)의 정의에서 출발할 수 있다.

${\displaystyle \nabla ^{2}{\vec{A}}=\nabla \left(\nabla \cdot {\vec}\right)+\nabla \times{\\becc}}}$

경사로로 어떤 기능을 구성하여 ID ${\displaystyle 매핑}$을 구성하려고 하기 때문에, 우리의 경우 ${\displaystyle \mathrm{case}}{\displaystyle \mathrm{}\times }$ A${\displaystyle \stackrel{}{}}$→${\displaystyle }$= ${\displaystyle \mathrm{curl}}$ ${\displaystyle }$ ${\displaystyle (A\stackrel{}{}}$→${\displaystyle }$)${\displaystyle }$= 0 ${\displaystyle \nabla$ \nabla $\time{\vec}=\operatorname$ {c$} \{\vec}\right$ 그러면 양쪽의 분열을 취할 수 있다.

${\displaystyle {\begin}\nabla \cdla \nabla \nabla \nabla \nabla \nabla \cdot {\\bec}\오른쪽)\\&=\nabla ^{2}\왼쪽(\nabla \cdot {\vec{A}\right)\\end{aigned}}}$

어떤 함수가 벡터 라플라시안의 고유함수인 경우, 그 발산성은 동일한 고유값을 가진 스칼라 라플라시안의 고유함수여야 함을 우리는 본다.Then we can build our inverse function ${\displaystyle \nabla ^{-1}}$ simply by breaking any function in ${\displaystyle \mathbb {H} _{3}}$ into the vector-Laplacian eigenbasis, scaling each by the inverse of their eigenvalue, and taking the divergence; the action of ${\displaystyle \nabla ^{-1}\c$$irc \nabla }$은(는) 그러므로 분명히 정체성이다$$.보조정리기를 쪼개면

${\displaystyle {\mathbb{H}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}\mathrm{im}}$ 임 ${\displaystyle }$(${\displaystyle \mathrm{curl}}$) ${\displaystyle \mathb {H} _{3}\cong L^{2}\plus \operatorname {im}(\operatorname {curl}$ $)\},$

또는 동등하게, ${\displaystyle {\mathrm{}}^{}}$ $3{\displaystyle {\mathbb{}}^{}}$ ${\$의 제곱합 통합 벡터 필드는 그라데이션과 컬의 합으로 나눌 수 있으며$$, 이것이 바로 우리가 입증하기 위해 시작한 것이다.null

특성.

분할 보조정리기에 따르면 정확한 순서가 짧을 경우

${\displaystyle 0\to A\;{\xrightarrow {\ f\}\;B\;{\xrightarrow {\ g\}}\;C\to 0}$

형태론 t : B → A에서는 t ∘ f가 정체성이거나, 형태론 u: C → B가 G ∘ u가 C에서는 정체성이라는 것을 인정하는 형태론 t : B → B가 A와 C의 직접적인 합계(비확정집단의 경우, 이것은 반간접적인 제품이다)를 인정한다.하나는 그렇게 짧은 정확한 순서가 갈라진다고 말한다.null

뱀 보조정리기는 정확한 두 행의 대응 도표가 어떻게 더 긴 정확한 순서를 만들어 내는지 보여준다.9개의 보조정리기는 특별한 경우다.null

5개의 보조정리기는 정확한 길이 5행의 정류 도표에서 중간지도가 이소모르프(Isomorphism)라는 조건을 제공하며, 짧은 5개의 보조정리도는 짧은 정확한 순서에 적용되는 특수한 경우다.null

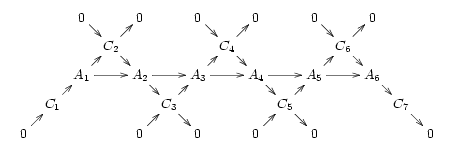
짧은 정확한 시퀀스의 중요성은 모든 정확한 시퀀스가 겹치는 몇 개의 짧은 정확한 시퀀스를 "함께 결합"함으로써 비롯된다는 사실에 의해 강조된다.예를 들어 정확한 시퀀스를 고려하십시오.

${\displaystyle A_{1}\to A_{2}\to A_{3}\to A_{5}\to A_{6}}}$

이 범주에 다음과 같은 물체 C가_k 존재한다는 것을 의미한다.

${\displaystyle C_{}}$ ${\displaystyle k_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \ker }$ ${\displaystyle }$ ${\displaystyle (A_{}}$ k${\displaystyle {}_{}}$→ ${\displaystyle {\mathrm{A}}_{}}$ k${\displaystyle {}_{}}$+ 1${\displaystyle {}_{}}$) ${\displaystyle \cong }$ ${\displaystyle \mathrm{im}}$ ${\displaystyle }$ ${\displaystyle ({\mathrm{A}}_{}}$ k${\displaystyle {}_{}}$- 1${\displaystyle {}_{}}$→ ${\displaystyle A_{}}$ k${\displaystyle {}_{}}$) $\displaystyle C_{k}\cong \ker(A_{k}\c}\$ck$+1$}\$cong \operatorname {im}(A_{k-1}\c_{k$

또한 각 형태론의 코커넬이 존재하며, 다음 형태론의 이미지에 이형성이 있다고 가정하자.

${\displaystyle C_{k}\cong \operatorname {coker}(A_{k-2}\to A_{k-1})$

(This is true for a number of interesting categories, including any abelian category such as the abelian groups; but it is not true for all categories that allow exact sequences, and in particular is not true for the category of groups, in which coker(f) : G → H is not H/im(f) but ${\displaystyle H/{\left\langle \o$$peratorname {im} f\right\rangele }^{H},$im(f)의 결합 폐쇄에 의한 H의 지수.그리고 나서 우리는 모든 대각선이 짧은 정확한 시퀀스인 정류 도표를 얻는다.

The only portion of this diagram that depends on the cokernel condition is the object ${\textstyle C_{7}}$ and the final pair of morphisms ${\textstyle A_{6}\to C_{7}\to 0}$. If there exists any object ${\displaystyle A_{k+1}}$ and morphism ${\displaystyle A_{k}$$\to A_{k+1}}$ such that ${\displaystyle A_{k-1}\to A_{k}\to A_{k+1}}$ is exact, then the exactness of ${\displaystyle 0\to C_{k}\to A_{k}\to C_{k+1}\to 0}$ is ensured.다시 집단의 범주의 예를 들어, im(f)이 H에 있는 어떤 동형성의 알맹이라는 사실은 그것이 그것의 결합 폐쇄와 일치하는 정상 부분군임을 암시한다. 따라서 coker(f)는 다음 형태론의 이미지 H/im(f)에 이형성이 있다.null

반대로, 겹치는 짧은 정확한 시퀀스의 목록을 보면, 그들의 중간 용어는 같은 방식으로 정확한 시퀀스를 형성한다.null

정확한 시퀀스 적용

아벨론 범주론에서 짧은 정확한 순서는 종종 하위 및 요인 객체에 대해 이야기할 수 있는 편리한 언어로 사용된다.null

연장 문제는 본질적으로 "단순히 정확한 수열의 최종 용어 A와 C를 고려할 때, B 중기에 어떤 가능성이 존재하는가?"라는 질문이다.그룹 범주에서 이것은 질문의 내용과 같다. 정상 부분군으로서 A를 갖는 그룹 B와 해당 요인 그룹으로서 C를 가지는 그룹은 무엇인가?이 문제는 집단의 분류에 중요하다.외부 자동형성 그룹을 참조하십시오.null

정확한 순서에서 f_i+1 ∘ f는_i A에서_i+2 A를_i 0으로 매핑하므로, 정확한 순서는 모두 연쇄 복합체라는 점에 유의한다.더욱이_i A 원소의 f-이미지만_i 0 by f로_i+1 매핑되기 때문에 이 체인 단지의 호몰로지(homology)는 미미하다.보다 간결하게:

정확한 순서는 정확하게 순환하는 체인 콤플렉스들이다.

그러므로 어떤 체인 콤플렉스를 고려했을 때, 그것의 동음이의학은 그것이 정확하지 않은 정도를 측정하는 것으로 생각할 수 있다.null

만일 우리가 체인 콤플렉스에 의해 연결된 일련의 짧은 정확한 시퀀스(즉, 체인 콤플렉스의 짧은 정확한 시퀀스 또는 다른 관점에서 짧은 정확한 시퀀스의 체인 콤플렉스)를 취한다면, 우리는 지그재그를 적용함으로써 호몰로학에 관한 긴 정확한 시퀀스(즉, 자연수에 의해 인덱싱된 정확한 시퀀스)를 도출할 수 있다. 보조정리법. 상대적 호몰로지 연구의 대수적 위상학에서 나온다. 메이어-베토리스 순서는 또 다른 예다.짧은 정확한 시퀀스에 의해 유도된 긴 정확한 시퀀스 또한 파생 펑터의 특성이다.null

정확한 functors는 정확한 시퀀스를 정확한 시퀀스로 변환하는 functors이다.null

참조

인용구

원천

• Spanier, Edwin Henry (1995). Algebraic Topology. Berlin: Springer. p. 179. ISBN 0-387-94426-5.
• Eisenbud, David (1995). Commutative Algebra: with a View Toward Algebraic Geometry. Springer-Verlag New York. p. 785. ISBN 0-387-94269-6.