해밀턴 분해

수학의 한 분야인 그래프 이론에서, 주어진 그래프의 해밀턴식 분해는 그래프의 가장자리를 해밀턴식 사이클로 분할한 것이다.해밀턴의 분해는 방향이 정해지지 않은 그래프와 지시된 그래프 모두에 대해 연구되어 왔다.간접적인 경우에서 해밀턴 분해는 각 요인이 연결되도록 그래프의 2-요인화라고도 설명할 수 있다.

필요조건

해밀턴 분해물이 비방향 그래프에 존재하려면 그래프를 연결하고 일정한 정도로 규칙적으로 만들어야 한다.그러한 분해가 있는 방향 그래프는 강하게 연결되어야 하며 모든 정점들은 서로 같은 도수와 도수가 같아야 하지만, 이 정도는 짝수일 필요가 없다.^[1]

4-정규 평면 그래프의 경우, 그리버그의 정리로부터 추가적인 필요한 조건을 도출할 수 있다.이러한 조건을 충족하지 못하고 해밀턴 분해되지 않는 4-정규 평면 그래프의 예는 허셜 그래프의 내적 그래프로 주어진다.^[2]

전체 그래프

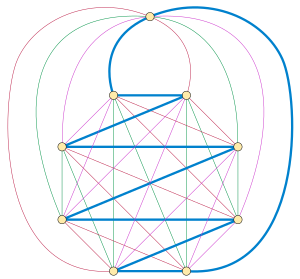
정점의 홀수 $n{\displaystyle }$ ${\displaystyle n}$을(를) 가진 모든 전체 그래프에는 해밀턴 분해가 있다.완성된 그래프를 이소모픽 2인자로 분해하는 오버울프치 문제의 특수한 경우인 이 결과는 1892년 에두아르 루카스가 왈레키에게 기인했다.Walecki의 건설은 정점의 $n$${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle n-1}$을 일반 폴리곤에 배치하고$,{\displaystyle }$ (n -${\displaystyle 1}$)/2 {\$displaystyle (n-1)/2}$ 폴리곤을 지그재그로 가로지르는 해밀턴$$ 경로의 이 부분 집합에 완전한 그래프를 포함하며, 각 경로는 $\pi {\displaystyle }$/${\displaystyle }$(${\displaystyle n}$- ${\displaystyle 1}$)의 배수로에서 서로 회전한다$.$$디스플레이$ 스타일 $\pi /(n-1$ .그리고 나서 그 길들은 남은 정점을 통해 그들의 끝을 연결함으로써 해밀턴 사이클로 모두 완성될 수 있다.^[3]

정규$$ 그래프의 정점을 ${\displaystyle \mathrm{2k}}$ ${\displaystyle 2k}$ - 정규 그래프의 정점을 2k ${\displaystyle 2k}$ 정점으로 확장하는 것은 그래프의 해밀턴 분해 여부를 변경할 수 없다.이 팽창 과정의 역행은 하나의 꼭지점까지 패밀리를 붕괴시키면서, 더 큰 그래프의 해밀턴식 분해는 원래 그래프의 해밀턴식 분해로 변모시킬 것이다.반대로 월레키의 구성은 클릭에 적용되어 작은 그래프의 해밀턴식 분해물을 확장된 그래프의 해밀턴식 분해로 확장할 수 있다.이 확장 과정은 해밀턴 분해물이 없는 고른 정도의 임의로 큰 정점 변환 그래프와 케이리 그래프를 만드는 데 사용될 수 있다.^[4]

완전한 그래프의 지시된 사례는 토너먼트다.1968년 폴 켈리의 추측에 답하면서 다니엘라 쿤과 데릭 오스트후스는 2012년 충분히 큰 정규 대회마다 해밀턴의 부패가 있다는 것을 증명했다.^[5][6]

분해 횟수

4개의 규칙적인 비방향 그래프마다 해밀턴의 분해 횟수가 짝수다.보다 강력한 것은 4-정규 그래프의 두$$ 에지 $e{\displaystyle }$ ${\displaystyle e}$과 $f{\displaystyle }$ ${\displaystyle f}$에 대해 $e{\displaystyle }$ ${\displaystyle e}$과 f ${\displaystyle f}$이(가) 동일한 사이클에 속하는$$ 해밀턴 분해 횟수가 짝수라는 것이다.${\displaystyle \mathrm{2k}}$ ${\displaystyle 2k}$ - 일반$$ 그래프가 해밀턴 분해의 3배 이상 요인 분해 횟수를 갖는 경우

$(3k-2)\cdot(3k-5)\cdots 7\cdot 4\cdot 1.}$

예를 들어 해밀턴 분해도를 갖는 4개 정규 그래프는 최소 4개, 해밀턴 분해도를 갖는 6개 정규 그래프는 최소 28개 등이다.해밀턴의 분해물이 독특한 유일한 그래프는 사이클 그래프라는 것이 뒤따른다.^[7]

계산 복잡성

임의 그래프의 해밀턴 분해 여부 테스트는 지시된 경우와 간접되지 않은 경우 모두 NP-완전하다.^[8]특히 문제는 지정된 짝수 수준의 정규 그래프(예: 4-정규 그래프)의 경우 NP-완전성이다.

입방 그래프의 선 그래프는 4-정규형이며, 기본 입방 그래프가 해밀턴 사이클을 갖는 경우에만 해밀턴 분해를 가진다.^[9][10]따라서 해밀턴 주기 문제의 하드 인스턴스의 선 그래프를 포함하는 그래프 클래스에 대해 해밀턴 분해는 NP-완전성을 유지한다.예를 들어, 해밀턴 분해는 입방 평면 그래프의 선 그래프를 포함하기 때문에 4개의 정규 평면 그래프의 경우 NP-완전하다.반면, 이러한 동등성은 4-정규 선 그래프의 기본 입방 그래프에 해밀턴 주기 문제가 있을 때 해밀턴 분해가 쉽다는 것을 의미하기도 한다.

짝수도의 랜덤 정규 그래프에는 거의 확실히 해밀턴식 분해가 존재하며, 더 강하게는 짝수도의 랜덤 정규 그래프를 입력하면 그 안에서 해밀턴식 분해를 거의 확실히 찾을 수 있는 랜덤화된 다항식 시간 알고리즘이 있다.^[11]

참고 항목

• 선형 수목성, 최대 2도의 하위 그래픽으로 제한된 다른 종류의 파티션

참조