헨데카그램

Hendecagram
헨데카그램
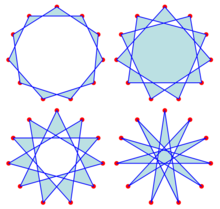HendecagramTypes.png
4개의 규칙적인 hendecagrams
모서리 및 정점11
슐레플리 기호{11/2}, {11/3}
{11/4}, {11/5}
콕시터-딘킨 도표CDel node 1.pngCDel 11.pngCDel rat.pngCDel d2.pngCDel node.png, CDel node 1.pngCDel 11.pngCDel rat.pngCDel d3.pngCDel node.png
CDel node 1.pngCDel 11.pngCDel rat.pngCDel d4.pngCDel node.png, CDel node 1.pngCDel 11.pngCDel rat.pngCDel d5.pngCDel node.png
대칭군디11, 주문 22
내부 각도(도)≈114.545° {11/2}
≈81.8182° {11/3}
≈49.0909° {11/4}
≈16.3636° {11/5}

기하학에서 헨데카그램(endeccaram 또는 엔데카그램)은 11개의 정점을 가진 별 폴리곤이다.

헨데카그램이라는 이름은 그리스 숫자 접두사인 헨데카-와 그리스 접미사 -그램이 결합되어 있다. 헨데카- 접두사는 그리스어 ἕν meaning greekα(ἕν + Δέα, 1 + 10)에서 유래한다. -gram 접미사는 선을 뜻하는 μαμμῆ(grammēs)에서 유래한다.[1]

정기 심박수

4개의 정기적인 hendecagram이 있는데,[2] 이것은 표기법 {11/2, {11/3}, {11/4}, {11/5}로 설명될 수 있다. 이 표기법에서 슬래시 뒤의 숫자는 가장자리로 연결된 점 쌍 사이의 단계 수를 나타낸다. 이 같은 네 가지 형태는 또한 보통의 암탉의 묘사로 간주될 수 있다.[3]

11이 프라임이기 때문에 모든 헨데카그램은 복합 형상이 아닌 별 폴리곤이다.

건설

주문이 뚜렷한 페르마 프라임의 생산품이 아닌 모든 홀수 일반 폴리곤과 별 폴리곤과 마찬가지로, 일반 헨데카그램은 나침반과 직선으로 구성될 수 없다.[4] 그러나 힐튼 앤 페더슨(1986)은 종이 조각으로 헨데카그램 {11/3}, {11/4}, {11/5}을(를) 만들기 위한 접이식 패턴을 기술하고 있다.[5]

적용들

포트 우드의 별 모양의 벽은 자유의 여신상의 밑받침이 되었다.

헨데카그램 {11/3} 및 {11/4}에 대한 프리즘은 DNA 분자의 모양을 대략적으로 나타내기 위해 사용될 수 있다.[6]

모미네 카툰 묘지의 11점짜리 별

현재 뉴욕시에 있는 자유의 여신상의 근거지인 포트 우드는 불규칙한 11점짜리 별 모양의 별 요새다.[7]

탑카프 스크롤에는 이슬람 예술에 사용된 11점짜리 별 기리 형태의 모습이 담겨 있다. 이 두루마리에 그 별 하나가 아닌 경우 hendecagram의 정기적인 형태지만 대신은 hendecagon의 가장자리가nearly-opposite 중간 지점에 hendecagon의 vertices 연결 라인을 이용한다.[8]11-pointed 스타 Girih 패턴도 Momine Khatun 영묘의 바깥쪽, 에릭 Broug은 패턴의``hig으로 간주될 수 있다고 쓴다. 사용된다.이슬람 기하학적 디자인의 h 포인트"[9]라고 말했다.

우주왕복선 고체 로켓 부스터에는 11개의 항성 모양의 단면이 로켓의 전방 부분(연료가 연소하는 내부 빈 공간)의 핵심에 사용되었다. 이 설계는 로켓이 음속 장벽을 통과하는 것과 거의 동시에 발사 초기 부분에서 더 많은 표면적과 더 큰 추력을 제공했으며, 별의 점이 연소된 후 더 느린 연소율과 감소된 추력을 제공했다.[10]

또한 인스타그램은 확인된 페이지를 구분하기 위해 파란색 일반 헨데카그램을 사용한다.

참고 항목

참조

별 다각형
  1. ^ Liddell, Henry George; Scott, Robert (1940), A Greek-English Lexicon: γραμμή, Oxford: Clarendon Press
  2. ^ O'Daffer, Phares G.; Clemens, Stanley R. (1976), Geometry: an investigative approach, Addison-Wesley, Exercise 7, p. 62, ISBN 9780201054200.
  3. ^ Agricola, Ilka; Friedrich, Thomas (2008), Elementary Geometry, Student mathematical library, vol. 43, American Mathematical Society, p. 96, ISBN 9780821890677.
  4. ^ Carstensen, Celine; Fine, Benjamin; Rosenberger, Gerhard (2011), Abstract Algebra: Applications to Galois Theory, Algebraic Geometry, and Cryptography, Sigma series in pure mathematics, vol. 11, Walter de Gruyter, p. 88, ISBN 9783110250084, On the other hand a regular 11-gon is not constructible.
  5. ^ Hilton, Peter; Pedersen, Jean (1986), "Symmetry in mathematics", Computers & Mathematics with Applications, 12 (1–2): 315–328, doi:10.1016/0898-1221(86)90157-4, MR 0838152
  6. ^ Janner, Aloysio (June 2001), "DNA enclosing forms from scaled growth forms of snow crystals", Crystal Engineering, 4 (2–3): 119–129, doi:10.1016/S1463-0184(01)00005-3
  7. ^ Adams, Arthur G. (1996), The Hudson River Guidebook, Fordham Univ Press, p. 66, ISBN 9780823216796.
  8. ^ Bodner, B. Lynn (2009), "The eleven–pointed star polygon design of the Topkapı Scroll", Bridges 2009: Mathematics, Music, Art, Architecture, Culture (PDF), pp. 147–154.
  9. ^ Broug, Eric (2013), Islamic Geometric Design, Thames & Hudson, p. 182
  10. ^ Angelo, Joseph A. (2009), Encyclopedia of Space and Astronomy, Infobase Publishing, p. 511, ISBN 9781438110189.

외부 링크