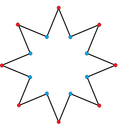
육각형

정육각형
정육각형
유형	정규 다각형
모서리 및 정점	16
슐레플리 기호	{16}, t{8}, tt{4}
콕시터-딘킨 도표
대칭군	디헤드랄(D16), 2×16 주문
내부 각도(도)	157.5°
특성.	볼록, 주기, 등변, 이등변, 동위원소

수학에서 육각형(육각형 또는 16곤이라고도 함)은 16면 다각형이다.^[1]

정육각형

정육각형은 모든 각도가 같고 모든 면이 합치되는 육각형이다. Schléfli 기호는 {16}이며 잘린 팔각형, t{8} 및 두 번 잘린 사각형 tt{4}로 구성할 수 있다. 잘린 육각형, t{16}는 3각형, {32}이다.

건설

16 = 2⁴ (2의 힘)로서, 일반적인 육각형은 나침반과 직선자를 사용하여 구성할 수 있다: 이것은 고대 그리스 수학자들에게 이미 알려져 있었다.^[2]

측정

일반 육각형의 각 각도는 157.5도이며, 어떤 육각형의 총 각도는 2520도이다.

가장자리 길이 t의 일반 육각형 영역은

${\displaystyle {\reasoned}A=4t^{2}\cot {\frac {\pi }{16}}=&4t^{2}\좌측(1+{\sqrt{2}}+{\sqrt{4+2}{\sqrt{\sqrt{2}}}\우측)\\=&4t^{2}({\sqrt{2}}+1)({\sqrt{4-2{\sqrt{2}}+1){\sqrt{2}}+1).\end{정렬}}}$

육각형에는 2의 힘인 여러 변이 있기 때문에 그 면적을 비에트의 공식을 잘라내서 할례 R의 관점에서 계산할 수 있다.

${\displaystyle A=R^{2}\cdot {\frac{2}}{1}\cdot {2}{\sqrt{2}}}\prac {2}}{\sqrt {2}{2+{\sqrt{2}}}=4R^{2-{\sqrt}}}}}}.}$

원주의 면적은 $\pi {\displaystyle }$ ${\displaystyle {R\mathrm{}}^{}}$ ${\displaystyle {}^{}}$,${\displaystyle \pi$ R$^{2}}}$이므로 정규$$ 육각형은 원주의 약 97.45%를 채운다.

대칭

대칭

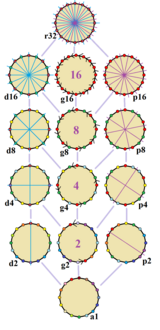정규 육각형의 14개의 대칭. 반사의 선은 정점을 통과하는 파란색, 가장자리를 통과하는 보라색이며 중심에는 회전 순서가 주어진다. 정점은 대칭 위치에 의해 색칠된다.

일반 육각형에는 Dih₁₆ 대칭, 순서 32가 있다. 4개의 이음 부분군이 있다. Dih₈, Dih₄, Dih₂, Dih₁, 그리고 5개의 순환 부분군: Z₁₆, Z₈₄, Z, Z₂, 그리고₁ 마지막은 대칭성이 없음을 암시한다.

일반 육각형에는 14개의 뚜렷한 대칭이 있다. 존 콘웨이는 완전한 대칭을 r32로 표시하며 어떤 대칭도 a1로 표시하지 않는다. 이음 대칭은 정점(대각의 경우 d) 또는 가장자리(직각의 경우 p)를 통과하느냐에 따라 구분된다. 중앙 열의 주기 대칭은 중심 교정 순서에 대해 g로 표시된다.^[3]

가장 일반적인 고대칭 육각형은 d16이며, 8개의 거울에 의해 구성된 등각 육각형은 길고 짧은 가장자리와 p16은 가장자리 길이가 같지만 정점이 두 개의 내부 각도를 교차하는 동위원소 육각형이다. 이 두 형태는 서로 이중으로 되어 있으며, 정육각형의 대칭 순서의 절반을 가지고 있다.

각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다. g16 부분군만 자유도는 없지만 지시된 가장자리로 볼 수 있다.

해부

16진법 투영법	112 롬브 해단
	정규	동위원소

Coxeter는 모든 조노곤(상대방이 평행하고 길이가 같은 2m-곤)을 m(m-1)/2 평행그램으로 해부할 수 있다고 명시하고 있다. ^[4] 특히 면적이 고르게 많은 일반 다각형의 경우, 이 경우 평행사변형은 모두 rhombi이다. 일반 육각형의 경우 m=8이며, 28:4 정사각형, 8 rhomb 3세트로 나눌 수 있다. 이 분해는 8큐브의 페트리 폴리곤 투영을 기반으로 하며, 1792면 중 28면이다. OEIS: A006245 목록에는 최대 16배 회전과 치랄 형태를 반영하여 1232944개의 솔루션 수가 열거되어 있다.

28마리의 늑대로 해부한다.

8시 15분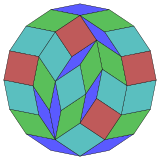

스큐 육각형

3개의 보통 꼬치 지그재그 육각형

{8}#{ }	{8⁄3}#{ }	{8⁄5}#{ }
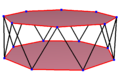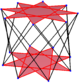일반적인 꼬치 육각형은 팔각형 항정신병, 팔각형 항정신병, 팔각형 교차 항정신병의 지그재그 가장자리로 보인다.

스큐 육각형은 24개의 정점과 가장자리가 있지만 동일한 평면에 존재하지 않는 스큐 다각형이다. 그러한 육각형의 내부는 일반적으로 정의되어 있지 않다. 꼬치 지그재그 육각형에는 두 평면이 번갈아 가며 정점이 있다.

일반 스큐 육각형은 가장자리 길이가 같은 정점 변환이다. 3차원에서는 지그재그 꼬치 육각형이 될 것이며, 동일한_8d D, [2⁺,16] 대칭, 순서 32의 팔각형 항정신병증의 정점과 측면 가장자리에서 볼 수 있다. 옥타그램 항정신병, s{2,16/3} 및 옥타그램 교차 항정신병, s{2,16/5}도 정규 꼬치 옥타곤을 가지고 있다.

페트리 폴리곤

일반 육각형은 많은 고차원 다상체를 위한 Petrie 폴리곤으로, 다음을 포함한 이러한 기울기 직교 돌출부에 나타나 있다.

A을15	B8		D9		2B2(4D)
159xx	8인조	8시 15분	611	161	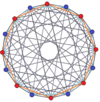8-8 듀오피라미드	8-8 듀오프리즘

관련숫자

헥사이드카그램은 기호가 {16/n}인 16면 별 다각형이다. 3개의 일반 별 다각형이 있는데, {16/3}, {16/5}, {16/7}은(는) 동일한 정점을 사용하지만, 3번째, 5번째 또는 7번째 지점마다 연결된다. 또한 세 가지 화합물이 있는데, {16/2}은(는) 2옥타곤으로 2{8}, {16/4}은(는) 4옥타곤으로 4{4}, {16/6}은(는) 2옥타그램으로 2{8/3}로 감소하고, 마지막으로 {16/8}은 8옥타곤으로 8{2}로 감소한다.

화합물 및 항성 육각체
형태	볼록 폴리곤	화합물	별 폴리곤	화합물
이미지	{16/1} 또는 {16}	{16/2} 또는 2{8}	{16/3}	{16/4} 또는 4{4}
실내각	157.5°	135°	112.5°	90°
형태	별 폴리곤	화합물	별 폴리곤	화합물
이미지	{16/5}	{16/6} 또는 2{8/3}	{16/7}	{16/8} 또는 8{2}
실내각	67.5°	45°	22.5°	0°

일반 옥타곤과 옥타그램의 더 깊은 절단은 정점과 두 개의 가장자리 길이의 등각형 중간 육각형 형식을 생성할 수 있다.^[5]

잘린 팔각형은 육각형이고 t{8}={16}. {8/7}(으)로 반전된 quasitrunculated 8각형은 16진수형이다. t{8/7}={16/7}. 잘린 옥타그램 {8/3}은(는) 육각형이고, {8/3}={16/3}이고, {8/5}(으)로 반전된 quasitrunculated 옥타그램은 육각형: t{8/5}={16/5}이다.

팔각형 및 팔각형의 등각 절단
퀘이레굴라속	등각			퀘이레굴라속
t{8}={16}				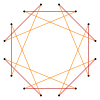t{8/7}={16/7}
t{8/3}={16/3}		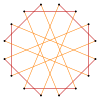		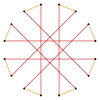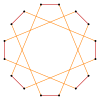t{8/5}={16/5}

예술에서

16세기 초 라파엘은 그의 그림에서 16면이라는 평범한 육각형의 원근상을 처음으로 구성했는데, 이것은 피에트로 페루치노의 이전 그림에서 8면 탑을 정교하게 묘사하였다.^[6]

육각문자(16면 별 다각형)는 알함브라에 있는 기리 패턴에 포함된다.^[7]

불규칙 육각형

팔각별은 오목한 육각형 별로 볼 수 있다.

참고 항목

• 룸블라인 네트워크

참조

외부 링크

• Weisstein, Eric W. "Hexadecagon". MathWorld.