접선 사각형

유클리드 기하학에서, 접선 사각형(때로는 그냥 접선 사각형) 또는 원곡선 사각형은 볼록한 사각형이며, 모든 면이 4각형 안에 있는 하나의 원과 접선될 수 있다. 이 원은 사방형 또는 그 새겨진 원의 근간이라고 불리고, 그 중심은 장려책이며, 반지름은 인라디우스라고 불린다. 이러한 사변측정감시들은 그들의 근간을 둘러싸거나 할례할 수 있기 때문에, 그것들은 또한 할례할 수 있는 사변측정감시, 할례할례할례할례할례할례할례, 할례할례할례할례할례할례할례할례할례, 할례할례할례할례할례할례할례할례할례할례할례할례로 불렸다.^[1] 접선 사변측정감시법은 접선 다각형의 특별한 경우다.

이 등급의 사변측정감시에 덜 자주 사용되는 다른 명칭은 격자형 사변형, 격자형 사변형, 내접형 사변형, 원주형 사변형 및 동일순환 사변형이다.^[1][2] 순환형 사각형 또는 내접형 사각형이라고 하는 원주형 4각형과는 혼동될 위험이 있기 때문에 마지막 5개의 이름 중 어느 것도 사용하지 않는 것이 바람직하다.^[1]

모든 삼각형에는 근근이 있을 수 있지만, 모든 사변측정감시원이 있는 것은 아니다. 접선이 될 수 없는 사각형의 예는 비제곱 직사각형이다. 아래의 섹션 특성은 4각형이 근친상간을 갖기 위해 반드시 충족해야 하는 필요조건과 충분한 조건을 명시한다.

특례

접선 사변측정감시법의 예로는 연이 있는데, 이 연은 광장을 포함하고, 광장을 포함한다. 연은 정확히 접선 사변측정감시선으로 교정치교정이기도 하다.^[3] 오른쪽 연은 원주가 있는 연이다. 4각형이 접선과 순환 둘 다인 경우에는 2각형 사다리꼴이라고 하고, 접선과 사다리꼴인 경우에는 접선 사다리꼴이라고 한다.

특성화

접선 사각형에서는 네 개의 각 이등분자가 근방의 중심에서 만난다. 반대로, 네 개의 각 이등분자가 한 지점에서 만나는 볼록한 사각형은 접선적이어야 하며 공통점은 인센티브다.^[4]

피토 정리에 따르면, 접선 사각형의 반대쪽 두 쌍은 동일한 총 길이로, 이것은 4각형의 반퍼미터와 같다.

${\displaystyle a+c=b+d={\frac {a+b+c+d}{2}}=s.}$

반대로 + c = b + d가 접선되어야 하는 볼록한 사각형.^{[1]: p.65 [4]}

사다리꼴이 아닌 볼록한 사각형 ABCD의 반대쪽이 E와 F에서 교차하는 경우, 다음^[4] 중 하나에 해당하는 경우에만 접선이다.

$[\디스플레이 스타일 \디스플레이 스타일 BE+]BF=DE+DF}$

또는

$[\displaystyle \displaystyle AE-EC=]AF-FC}$

이것들 중 두 번째는 우르쿠하트의 정리에 있는 동일성의 하나와 거의 같다. 유일한 차이점은 양쪽의 징후들이다; 우르쿠하트의 정리에는 차이 대신에 합계가 있다.

또 다른 필요하고 충분한 조건은 두 삼각형 ABC와 ADC의 경사가 서로 접하는 경우에만 볼록한 사각형 ABCD가 접선된다는 것이다.^{[1]: p.66}

대각선 BD와 4면 ABCD에 의해 형성된 각도에 대한 특성화는 이오시페스쿠에 기인한다. 그는 1954년에 볼록한 사면이 만약의^[5] 경우에 한해서만 근골이 있다는 것을 증명했다.

${\displaystyle \tan {\frac {\angle ABD}{2}}\cdot \tan {\frac {\angle BDC}{2}}=\tan {\frank ADB}{2}}\cdot \tan {\frac {\angle DBC}{2}}}}}}}}}}}.}$

또한, 연속적인 면 a, b, c, d를 가진 볼록한 사각형은 만약의 경우만 접선이다.

${\displaystyle R_{a}R_{c}=R_{b}R_{d}}}}$

여기서 R_a, R_b, R, R은_cd 각각 a, b, c, d 면에 외부적으로 접하는 원의 반지름이며 각 면에 대해 인접한 두 면의 연장이다.^{[6]: p.72}

대각선에 의해 형성된 네 개의 하위 계통에서 몇 가지 더 특성화가 알려져 있다.

특수선 세그먼트

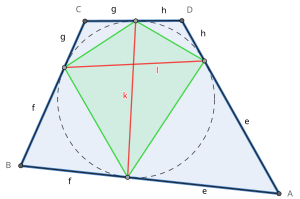
접선 사각형의 8 접선 길이(오른쪽 그림에서 e, f, g, h)는 꼭지점에서 근골이 측면에 접하는 지점까지의 선 세그먼트다. 각 꼭지점에는 두 개의 합치 탄젠트 길이가 있다.

접선 사각형의 두 개의 접선 코드(k와 l)는 근골이 이 변에 접하는 반대편의 점을 연결하는 선 세그먼트다. 이것들은 또한 접촉 사각형의 대각선이다.

면적

비트리거 공식

접선 사각형의 면적 K는 다음과 같다.

${\displaystyle \displaystyle K=r\cdot s,}$

여기서 s는 반퍼미터, r은 인라디우스다. 또^[7] 다른 공식은

${\displaystyle \displaystyle K={\tfrac {1}{2}}: {\sqrt{p^{2}q^{2}-(ac-bd)^{2}}:$

대각선 p, q 및 면 a, b, c, d의 면적에 접선 사각형의 면적을 제공한다.

면적은 또한 네 개의 접선 길이로 표현될 수 있다. 만약 이것들이 e, f, g, h라면, 접선 사각형은 면적을^[3] 가진다.

${\displaystyle \displaystyle K={\sqrt {(e+f+g+h)(efg+fgh+ghe+hef)}}.}$

또한 접선 사각형의 면적은 면 a, b, c, d 및 연속 접선 길이 e, f, g, h를 기준으로^{[3]: p.128} 표현할 수 있다.

${\displaystyle K={\sqrt {abcd-(eg-fh)^{2}}.}$

eg = fh 만약의 경우 그리고 만약 2등변형이 또한 순환적이고 따라서 2등변형인 경우,^[8] 이것은 최대 $영역{\displaystyle \sqrt{}}$ ${\displaystyle \sqrt{a}}$ b ${\displaystyle \sqrt{c}}$ d ${\${\$sqrt{abcd}}}$이(가) 2등변형인 경우에만 발생함을$$ 보여준다.

삼각 공식

면 a, b, c, d 및 두 개의 반대 각도에서 면적에 대한 삼각 공식은 다음과^{[7][9][10][11]} 같다.

${\displaystyle \displaystyle K={\sqrt {abcd}\sin{\frac {A+C}{2}}={\sqrt{abcd}}\sin {\frac {B+D}{2}}}.}$

주어진 측면 길이에 대해, 사각형이 또한 순환적이고 따라서 2중 4각형인 경우 면적이 최대가 된다. 그$$ 다음 $K{\displaystyle }$= ${\displaystyle b\sqrt{}}$ ${\displaystyle \sqrt{c}}$ ${\displaystyle \sqrt{d}}$ ${\$ K$={\sqrt {abcd}}.$ 반대 각도는 보조 각이기 때문이다. 이것은 미적분을 이용하여 다른 방법으로 증명될 수 있다.^[12]

두 개의 반대 각도를 포함하는 접선 사각형 ABCD 영역에 대한 또 다른 공식은^{[10]: p.19}

$K=\왼쪽(IA\cdot IC+)IB\cdot ID\오른쪽)\sin {\frac {A+C}{2}}:}$

내가 인센티브를 주는 곳이지

실제로 면적은 인접한 두 변과 두 개의 반대 각도로 표현될^[7] 수 있다.

${\displaystyle K=ab\sin {\frac {B}{2}}\csc {\frac {D}{2}}\sin {\frac {B+D}{2}.}$

여전히^[7] 또 다른 영역 공식은

${\displaystyle K={\tfrac {1}{1}:{2}}(ac-bd)\tan {\theta },}$

여기서 θ은 대각선 사이의 각도 중 하나이다. 이 공식은 접선 사각형이 연인 경우 사용할 수 없으며, 이때 θ은 90°이고 접선 함수가 정의되지 않기 때문이다.

불평등

위에서 간접적으로 언급했듯이, 측면 a, b, c, d가 있는 접선 사각형의 면적이 충족된다.

${\displaystyle K\leq {\sqrt {abcd}}$

2등분 4각형일 경우에만 동등하게.

T. A. 이바노바(1976년)에 따르면, 접선 사각형의 반퍼미터 s는 만족한다.

$(\displaystyle s\geq 4r}$

여기서 r은 인라디우스다. 4각형이 정사각형일 경우에만 평등이 있다.^[13] 이는 K = r 면적에 대해 불평등이 있다는 것을 의미한다.

${\displaystyle K\geq 4r^{2}}$

접선 사각형이 정사각형인 경우에만 동등하게.

파티션 속성

네 개의 선은 네 개의 오른쪽 연으로 4각형의 칸막이에 접하는 지점과 4각형의 중심 사이의 구획이다.

만약 선 하나가 접선 사각형을 동일한 면적과 동일한 경계를 가진 두 개의 다각형으로 자른다면, 그 선은 인센티브를 통과한다.^[4]

인라디우스

연속된 면이 a, b, c, d인 접선 사각형의 인라디우스는 다음과^[7] 같이 주어진다.

${\displaystyle r={\frac {K}{s}}={\frac {K}{a+c}={\frac {K}{b+d}}}}}}}}$

여기서 K는 4각형의 영역이고 s는 반퍼미터다. 주어진 면이 있는 접선 사각형의 경우, 사각형도 순환할 때(따라서 이등변 4각형) 반경은 최대값이다.

접선 길이로 볼 때, 근방은 반지름을^{[8]: Lemma2 [14]} 가지고 있다.

${\displaystyle \displaystyle r={\sqrt {\frac {efg+fgh+ghef}{e+f+g+h}}.}$

또한 inradius는 자극자 I에서 접선 사각형 ABCD의 정점까지의 거리로 표현할 수 있다. u = AI, v = BI, x = CI 및 y = DI인 경우

${\displaystyle r=2{\sqrt {\frac(\frac)(\fraca -uvx)(\flasma -xy)(\flasma -xy)}{uvxy(ux+vy)(uyy+vy)}}}}}}$

여기서 $\sigma {\displaystyle }$= ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{2}{}(u}$ v ${\displaystyle x}$+ ${\displaystyle v}$ x ${\displaystyle y}$+ y + y ${\displaystyle x}$ ${\displaystyle y}$ + ${\displaystyle yu}$) ${\displaystyle \sigma ={\tfrac{1}:{2}}(uvx+vxy+xyu+$yu+$yuv$^[15] .

삼각형인 ABC, BCD, CDA, DAB의 경사가 각각$$ radii ${\displaystyle {r\mathrm{}}_{}}$ 1,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle {}_{}{r\mathrm{}}_{}}$ ${\displaystyle {}_{}}$,${\displaystyle {}_{}}$r ${\displaystyle {4\mathrm{}}_{}}$ ${\$},$r_{3},r_{4}$를 갖는 경우 접선 사각형 ABCD의 인라디우스는 다음과 같이 주어진다.

${\displaystyle r={\frac {G+{\sqrt{G^{2}-4r_{1}r_{1}r_{3}r_{4}(r_{1}r_{3}+r_{2}r_{4})}}}}}}{2(r_{1}r_{1}r_{2}r_{2}r_{4}}}}})}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

where ${\displaystyle G=r_{1}r_{2}r_{3}+r_{2}r_{3}r_{4}+r_{3}r_{4}r_{1}+r_{4}r_{1}r_{2}}$.^[16]

각도 공식

e, f, g, h가 각각 정점 A, B, C, D에서 접선 4각형 ABCD의 면에 근골이 접선되는 지점까지의 접선 길이인 경우, 4각형의 각도는 다음과^[3] 같이 계산할 수 있다.

${\displaystyle \sin {\frac {A}{2}}={\sqrt {\frac {efg+fgh+ghef}{(e+f)(e+g)(e+h)}}},}$

${\displaystyle \sin {\frac {B}{2}}={\sqrt {\frac {efg+fgh+ghef}{(f+e)(f+g)(f+h)}}}},}$

${\displaystyle \sin {\frac {C}{2}}={\sqrt {\frac {efg+fgh+ghef}{(g+e)(g+f)(g+h)}}}},}$

${\displaystyle \sin{\frac {D}{2}}={\sqrt {\fg+fgh+gh+ghef}{(h+e)(h+f)}}}}}.}$

접선 코드 k와 l 사이의 각도는 다음과^[3] 같다.

${\displaystyle \sin {\varphi }={\sqrt {(e+f+g+h)}(efg+fgh+gh+hhef)}{(e+f)(g+h)(h+e)}}}}}}.}$

대각선

e, f, g, h가 각각 A, B, C, D에서 접선 4각형 ABCD의 측면에 접선되는 지점까지의 접선 길이인 경우, 대각선 p = AC, q = BD의 길이는 다음과^{[8]: Lemma3} 같다.

${\displaystyle \p={\sqrt {{\frac {e+g}{f+h}{{f+h}}{\Big (}e+g)(f+h)+4fh{\Big )}}}},}$

${\displaystyle \displaystyle q={\sqrt {{\frac {f+h}{e+g}{\Big(}e+g)(f+h)+4eg{\)큰 )}}}.}$

접선 화음

e, f, g, h가 접선 사각형의 접선 길이라면 접선 화음의 길이는 다음과 같다^[3].

${\displaystyle \displaystyle k={\frac {2(efg+fgh+ghe+hef)}}{\sqrt {(e+f)(g+h)(e+g)(f+h)}}}}}$

${\displaystyle \displaystyle l={\frac {2(efg+fgh+ghe+hef)}}{\sqrt {(e+h)(f+g)(e+g)(f+h)}}}}}}}}}$

여기서 길이 k의 접선 화음은 길이 a = e + f와 c = g + h를 연결하고, 길이 l의 한쪽은 길이 b = f + g 및 d = h + e의 측면을 연결한다. 접선 코드의 제곱비가 만족함^[3]

${\displaystyle {\frac{k^{2}}:{l^{2}}={\frac {bd}{ac}}}}.}$

두 개의 접선 화음

• 접선 사각형에도 원주가 있는 경우에만 직각이다(이중 원).^{[3]: p.124}
• 접선 사각형이 연일 경우에만 길이가 같다.^{[17]: p.166}

접선 사각형 ABCD에서 AB와 CD 사이의 접선 화음은 AB와 CD 사이의 바이메디언이 BC와 DA 사이의 그것보다 짧은 경우에만 더 길다.^{[18]: p.162}

접선 사각형 ABCD에 접선점 W가 있고 접선 코드 WY가 M에서 대각선 BD와 교차하는 경우 접선 $길이$의 비율 B W D$$Y {\$displaystyle {\tfrac {BW}{$$DY}}$은(는) 대각선 BD 세그먼트의 비율$$ B $M{\displaystyle \frac{}{}}$ ${\displaystyle \frac{D}{}}$ ${\displaystyle \frac{M}{}}$ ${\$과(와) 같다.^[19]

시준점

M과₁ M이₂ 장려자 I와 함께 접선 사각형 ABCD에서 각각 대각선 AC와 BD의 중간점이고, 반대편의 쌍이 JK의 중간점인 상태에서₃ J와 K에서 만나면 M₃, M₁, I, M₂ 포인트는 서로 평행하게 된다.^{[4]: p.42} 그것들을 포함하는 선은 4각형의 뉴턴 선이다.

접선 사각형의 반대쪽 확장이 J와 K에서 교차하고, 접선 사각형의 반대쪽 확장이 L과 M에서 교차하는 경우, J, L, K, M의 네 점은 일직선으로 교차한다.^{[20]: Cor.3}

만약 내접원 옆은 AB형, BC, CD, DAT1T2T3, T4에서 각각, 이러한 점의 대응하는 변(그것은, AT1)BN1 등등)에 관해서 만약 N1, N2, N3, N4 있는isotomic와 같은 관계에 닿아 있다면, 그 접선 네 변의 네 이걸 점이 선 N1N3과 N2N4의 교차점으로 정의된다.둘 다 이런 종의 나누었다. 4각형의 둘레가 두 개의 동일한 부분으로 되어 있다. 더 중요한 것은, Nagel 지점 N, "면적 중심" G, 그리고 인센티브 I가 이 순서에 따라 일치하며, NG = 2GI이다. 이 선은 접선 사각형의 나겔 선이라고 불린다.^[21]

자극자 I과 대각선이 P에서 교차하는 접선 사각형 ABCD에서는 H_X, H_Y, H, H를_ZW AIB, BIC, CID, DIA 삼각형의 직교자가 되도록 한다. 그러면 P, H_X, H_YZ, H, H_W 점들이 일직선이다.^{[10]: p.28}

동시선 및 수직선

두 개의 대각선과 두 개의 접선 화음은 동시에 나타난다.^{[11][10]: p.11} 이것을 볼 수 있는 한 가지 방법은 브리안콘의 정리의 제한적인 사례로서, 모든 면이 하나의 원뿔 부분에 접하는 육각형에는 한 점에서 만나는 세 개의 대각선이 있다고 기술하고 있다. 접선 사각형으로부터, 두 개의 정점을 접선의 두 반대 지점에 놓음으로써, 두 개의 180° 각도로 육각형을 형성할 수 있다; 이 육각의 6개 면은 모두 새겨진 원에 접하는 선에 놓여있기 때문에 대각선은 한 점에서 만난다. 그러나 이 대각선 중 두 개는 접선 사각형의 대각선과 같고, 육각의 세 번째 대각선은 접선의 두 반대 지점을 통과하는 선이다. 이 같은 주장을 다른 두 개의 접선 지점과 반복하면 결과의 증거가 완성된다.

만약 접선 사각형의 반대편의 확장이 J와 K에서 교차하고 대각선이 P에서 교차한다면, JK는 내가 유인자인 IP의 확장에 수직이다.^{[20]: Cor.4}

장려자

접선 사각형의 인센티브는 (대각선의 중간점을 연결하는) 뉴턴 선에 있다.^{[22]: Thm. 3}

접선 사각형에서 두 반대편의 비율은 다음과 같은 유도체^{[10]: p.15} I과 정점 사이의 거리로 표현할 수 있다.

${\displaystyle {\frac {AB}{CD}}={\frac {IA\cdot IB}{IC\cdot ID},\quad \quad {\frac {BC}{DA}}={\frac {IB\cdot IC}{ID\cdot IA}.}$

내가^[23] 만족하는 인센티브를 가진 접선 사각형 ABCD에서 인접한 두 변의 제품

$AB\cdot BC=IB^{2}+{\frac {IA\cdot IB\cdot IC}{ID}}.}$

만약^{[10]: p.16} 내가 접선 사각형 ABCD의 인센티브라면,

$[\displaystyle IA\cdot IC+)IB\cdot ID={\sqrt {AB\cdot BC\cdot CD\cdot DA}.}$

접선 사각형 ABCD에서 인센티브자 I은 다음과^{[10]: p.22} 같은 경우에만 4각형의 "Vertex centroid"와 일치한다.

$[\displaystyle IA\cdot IC=)IB\cdot ID.}$

M과_p M이_q 장려자 I가 있는 접선 사각형 ABCD에서 대각선 AC와 BD의 중간점이라면,

${\displaystyle {\frac {IM_{p}}{{p}}{{p}}IM_{q}}={\frac {IA\cdot IC}{IB\cdot ID}}={\frac {e+g}{f+h}}}}$

여기서 e, f, g, h는 각각 A, B, C, D에서 접선 길이다. 첫 번째 동일성과 이전 특성을 결합하여, 장려자가 대각선의 중간점을 연결하는 선 부분의 중간점인 경우에만, 접선 사각형의 "Vertex centroid"는 인센티브 제공자와 일치한다.

4-bar 연계가 접선 사각형의 형태로 이루어진다면, 4-bar 연계가 볼록하게 유지된다면, 어떻게 접선 상태로 유지될 것이다.^[25][26] (예를 들어, 사각형이 더 작은 근골에도 접선 상태로 유지된다.) 한쪽 면이 고정된 위치에 있는 경우, 4각형이 구부러질 때, $인센티브$는 ${\displaystyle \sqrt{b}}$ ${\displaystyle \sqrt{c}}$ d${\displaystyle /s}${\d $디스플레이$ 스타일 {\$sqrt{abcd}/s}$ 반경의 원을 추적한다. 여기서 a,b,c,d는 순차적으로 면이고 s는 반퍼미터다.

4개 하위 그룹의 특성화

대각선이 P에서 교차하는 볼록한 사각형 ABCD에서 대각선에 의해 형성된 비과대각 삼각형 APB, BPC, CPD, DPA에는 다음과 같은 접선 사변측정감시 특성이 있다.

let₁ r₂, r₃, r₄, r은 각각 4개의 삼각형 APB, BPC, CPD, DPA에 있는 경골의 반지름을 나타낸다. 차오와 시메오노프는 사면이 만약의^[27] 경우에 한해서만 접선한다는 것을 증명했다.

${\displaystyle {\frac {1}{r_{1}}+{\frac {1}{1}{3}}={\frac {1}{r_}}+{\frac {1}{1}{4}}}}}}}.}$

이러한 특성화는 이미 Vaynshtejn에 의해 5년 전에 증명되었다.^{[17]: p.169 [28]} 그의 문제에 대한 해결책에서는 바실리예프와 센데로프가 비슷한 성격화를 주었다. h₁, h₂, h₃, h, h가₄ 동일한 4개의 삼각형(대각선 교차로에서 4각형의 측면까지)에서 고도를 나타내는 경우, 4각형은 만약의 경우 및 단지 다음과^[5][28] 같은 경우에만 접선된다.

${\displaystyle {\frac {1}{h_{1}}+{\frac {1}{3}}}={\frac {1}{h_{2}}+{\frac {1}{1}{4}}}}}}}}.}$

또 다른 유사한 특성은 동일한 4개의 삼각형(각 4개의 exradi r_a, r_b, r_c 및 r_d)에 있는 exradiii r, r, r 및 r과 관련이 있다(각각 4개의 excircle은 4각형의 한 면과 대각선의 확장에 접선한다). 4각형은 만약의^{[1]: p.70} 경우만 접선이다.

${\displaystyle {\frac {1}{r_{a}}+{\frac {1}{r_{c}}={\frac {1}{r_{b}}+{\frac {1}{1}{d}}}}}}.}$

R₁, R₂, R₃, R이₄ 각각 3각형 APB, BPC, CPD, DPA의 원곡선에 있는 반지름을 나타내는 경우, 4각형 ABCD는 만약의 경우 및 다음의 경우에만^{[29]: pp. 23–24} 접선된다.

${\displaystyle R_{1}+R_{3}=R_{2}+R_{4}}$

1996년, Vaynshtejn은 아마도 여러 잡지와 웹사이트에 나중에 등장한 접선 사분면 측정기의 또 다른 아름다운 특성을 입증한 최초의 인물이었을 것이다.^{[1]: pp. 72–73} 그것은 볼록한 사각형이 그것의 두 대각선에 의해 4개의 겹치지 않는 삼각형으로 나뉘어질 때, 4개의 삼각형의 장려자는 만약 4개의 삼각형이 접선된다면 그리고 오직 4개의 삼각형의 장려자가 순환한다고 말한다. 사실, 장려책들은 교정치각형 순환 4각형을 형성한다.^{[1]: p.74} 관련 결과, 경골은 동일한 삼각형(사방형의 측면과 대각선의 확장에 접선)으로 경골과 교환할 수 있다. 따라서 볼록한 4각형은 만약 이 네 개의 외각의 중심선이 주기적인 4각형의 정점일 경우에만 접선된다.^{[1]: p. 73}

대각선이 P에서 교차하는 볼록한 사각형 ABCD는 정점 B와 D의 반대편에 있는 4개의 삼각형에서 4개의 엑센서가 일치할 경우에만 접선된다.^{[1]: p. 79} R_a, R_b, R_c, R이_d 각각 정점 B와 D의 반대편에 있는 삼각형 APB, BPC, CPD, DPA의 exradii인 경우, 다른 조건은 4각형이 만약의 경우와 만약의^{[1]: p. 80} 경우만 접선이라는 것이다.

${\displaystyle {\frac {1}{R_{a}}+{\frac {1}{{1}{c}}={\frac {1}{R_{b}}+{\frac {1}{1}{R_{d}}}}}.}$

또한, 대각선이 P에서 교차하는 볼록한 사각형 ABCD는 만약의 경우 또는 다음의^[5] 경우에만 접선된다.

${\displaystyle{\frac {a}{\triangle (APB)}}}+{\frac {c}{\triangle (CPD)}}}}={\frac {b}{\triangle (BPC)}}+{\frac {d}{\triangle (DPA)}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

여기서 ∆(APB)는 삼각형 APB의 영역이다.

대각선 교차로 P가 대각선 AC를 AP = p와₁ PC = p로₂ 나누는 세그먼트를 나타내고, 이와 유사하게 P는 대각선 BD를 세그먼트 BP₁ = q와 PD₂ = q로 나눈 다음, 다음과 같은 동일성 중 하나라도 참일 경우에만 사각형이 접선된다.^[30]

${\displaystyle ap_{2}q_{2}+cp_{1}q_{1}q_{1}=bp_{1}q_{1}{2}+dp_{2}q_{1}:{1}:{1}:{1}}}}}$

또는^{[1]: p. 74}

${\displaystyle {\frac {(p_{1}+q_{1}-a)(p_{2}+q_{2}-c)}{(p_{1}+q_{1}+a)(p_{2}+q_{2}+c)}}={\frac {(p_{2}+q_{1}-b)(p_{1}+q_{2}-d)}{(p_{2}+q_{1}+b)(p_{1}+q_{2}+d)}}}$

또는^{[1]: p. 77}

${\displaystyle {\frac {(a+p_{1}-q_{1})(c+p_{2}-q_{2})}{(a-p_{1}+q_{1})(c-p_{2}+q_{2})}}={\frac {(b+p_{2}-q_{1})(d+p_{1}-q_{2})}{(b-p_{2}+q_{1})(d-p_{1}+q_{2})}}.}$

접선 사각형이 다른 유형의 사각형이어야 하는 조건

마름모꼴

접선 사각형은 반대 각도가 같은 경우에만 광맥버스다.^[31]

연

접선 사각형은 다음 조건 중 하나라도 사실인 경우에만 연이다.^[17]

• 그 지역은 대각선의 절반의 산물이다.
• 대각선은 수직이다.
• 접선의 반대 지점을 연결하는 두 선 세그먼트의 길이는 동일하다.
• 반대쪽 접선 길이의 한 쌍은 길이가 같다.
• 바이메디언들은 길이가 같다.
• 반대편의 생산품은 동일하다.
• 근골의 중심은 대칭의 축인 대각선에 놓여 있다.

이등변 4각형

근골이 각각 W, X, Y, Z에서 측면 AB, BC, CD, DA에 접하는 경우, 접선 사각형 ABCD도 다음 조건 중 하나가 유지되는 경우에만 순환(따라서 2원형)된다.^{[2][3]: p.124 [20]}

• WY는 XZ에 수직이다.
• $[\displaystyle AW\cdot CY=BW\cdot DY}$
• ${\displaystyle {\frac {AC}{BD}}={\frac {AW+CY}{BX+DZ}}}$

이 세 가지 중 첫 번째는 접점 사각형 WXYZ가 교정치각형 사각형임을 의미한다.

접선 사각형은 그것의 인라디우스가 동일한 옆 길이 순서를 가진 다른 접선 사각형의 그것보다 더 큰 경우에만 이등변이다.^{[32]: pp.392–393}

접선 사다리꼴

만약 근골이 각각 W와 Y에서 측면 AB와 CD에 접하는 경우, 접선 사각형 ABCD는 평행 측면^{[33]: Thm. 2} AB와 CD가 있는 사다리꼴이다.

$[\displaystyle AW\cdot DY=BW\cdot CY}$

그리고 AD와 BC는 사다리꼴의 평행한 면이다.

$[\displaystyle AW\cdaystyle AW\cdot BW=CY\cdot DY.}$

참고 항목

• 원곡선
• 탕전위 4각형
• 접선 삼각형
• 접선 다각형

참조

외부 링크

위키미디어 커먼스는 접선 사분면 측정과 관련된 미디어를 보유하고 있다.

• Weisstein, Eric W., "Tangential Quadrilateral", MathWorld