육각 프리즘
Hexagonal prism| 균일한 육각 프리즘 | |
|---|---|
 | |
| 유형 | 프리즘 균일 다면체 |
| 요소들 | F = 8, E = 18, V = 12(수평 = 2) |
| 옆얼굴 | 6{4}+2{6} |
| 슐레플리 기호 | t{2,6} 또는 {6}×{} |
| 와이토프 기호 | 2 6 2 2 2 3 |
| 콕시터 도표 | |
| 대칭 | D6h, [6,2], (*622), 주문 24 |
| 회전군 | D6, [6,2],+ (622), 주문 12 |
| 참조 | U76(d) |
| 이중 | 육각 디피라미드 |
| 특성. | 볼록한 조노헤드론 |
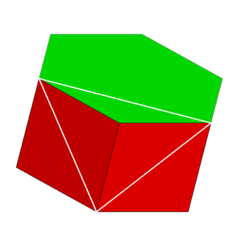 정점수 4.4.6 | |
기하학에서 육각 프리즘은 육각기반이 있는 프리즘이다. 이 다면체는 8개의 면, 18개의 가장자리, 12개의 꼭지점을 가지고 있다.[1]
얼굴이 8개여서 팔면체다. 그러나 팔면체라는 용어는 주로 8개의 삼각형 면을 가진 정규 팔면체를 가리킬 때 사용된다. 옥타헤드론이라는 용어의 애매함과 다양한 8면체의 유사성 때문에 그 용어는 설명 없이 거의 사용되지 않는다.
깎기 전에, 많은 연필들은 긴 육각 프리즘의 모양을 취한다.[2]
반정형(또는 균일) 다면체로서
얼굴이 모두 규칙적인 경우, 육각 프리즘은 반정형 다면체로서, 보다 일반적으로는 획일적인 다면체로서, 정사각형 면과 두 개의 일반 다각형 캡으로 이루어진 무한대의 프리즘 집합에서 네 번째가 된다. 잘린 육각형 호소헤드론(Schléfli 기호 t{2,6})으로 볼 수 있다. 또는 일반 육각형 및 라인 세그먼트의 데카르트 제품으로 볼 수 있으며, {6}×{} 제품으로 표현된다. 육각 프리즘의 이중은 육각형 비피라미드다.
오른쪽 육각 프리즘의 대칭 그룹은 순서 24의 D이다6h. 회전 그룹은 순서 12의 D이다6.
볼륨
대부분의 프리즘에서와 같이, 볼륨은 베이스의 면적을 의 측면 길이로 하여 h{\h}에 곱하여 다음과 같은 공식을 제공한다[3]
대칭
균일한 육각 프리즘의 위상은 다음과 같은 하부 대칭의 기하학적 변화를 가질 수 있다.
| 이름 | 정각 프리즘 | 육각형 좌상 | 직교 프리즘 | 삼암 프리즘 | 직교 트라페조프리즘 |
|---|---|---|---|---|---|
| 대칭 | D6h, [2,6], (*622) | C6v, [6], (*66) | D3h, [2,3], (*322) | D3d, [2+,6], (2*3) | |
| 건설 | {6}×{}, | t{3}×{}, | s2{2,6}, | ||
| 이미지 |  |  | 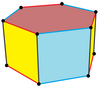 |  | |
| 왜곡. |  |  |   |  | |
공간 테셀레이션의 일부로
그것은 3차원 4개의 프리즘 균일 볼록 벌집의 세포로 존재한다.
| 육각 프리즘 벌집[1] | 삼각헥사각 프리즘 벌집 | 스너브 삼각 헥스각 프리즘 벌집 | Rhombitriangular-hexangel 프리즘 벌집 |
 | 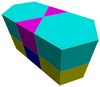 |  | 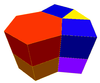 |
또한 다음을 포함한 다수의 4차원 균일 4폴리탑의 세포로도 존재한다.
| 잘린 사면 프리즘 | 잘린 팔면 프리즘 | 잘린 큐옥타헤드랄 프리즘 | 잘린 이두면 프리즘 | 잘린 이코시다데카헤드랄 프리즘 |
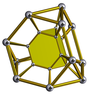 | 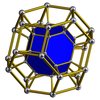 | 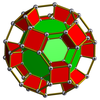 |  |  |
| 구획 5셀 | 잡동사니 5세포 | 구획 16셀 | 잡탕의 정방체 | |
 |  |  |  | |
| 24구경. | 전지 24셀 | 6백 셀을 달리다. | 다량의 120셀 | |
 |  |  |  |
관련 다면체 및 틸팅
| 균일한 육각형 이면구형 다면체 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 대칭: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||
 |  |  |  |  |  |  | ||||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | s{2,6} | ||||||
| 듀얼 투 유니폼 | ||||||||||||||
 |  |  |  |  |  |  |  |  | ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
이 다면체는 꼭지점 수치(4.6.2p)와 Coxeter-Dynkin 도표를 가진 일련의 균일한 패턴의 구성원으로 간주될 수 있다. p < 6의 경우, 시퀀스의 구성원은 구면 기울기로서 아래에 표시된 전위절제 다면체(조노헤드론)이다. p > 6의 경우 잘린 3헥타르 타일링부터 시작하여 쌍곡면의 기울기이다.
| *n32 전분해 틸팅의 대칭 변이: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] | 구면 | 유클리드 | 콤팩트 하이퍼브. | 파라코. | 비대칭 쌍곡선 | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3] | *∞32 [∞,3] | [12i,3] | [9i,3] | [6i,3] | [3i,3] | |
| 수치 |  |  |  |  |  |  |  |  |  |  |  | |
| 구성. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| 듀얼스 |  |  |  |  |  |  |  |  |  |  |  |  |
| 구성. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.1987 | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
참고 항목
| 프리즘 이름 | 디조날 프리즘 | (트리거) 삼각 프리즘 | (Tetrangle) 사각 프리즘 | 오각형 프리즘 | 육각 프리즘 | 헵타곤 프리즘 | 팔각 프리즘 | 엔네오각 프리즘 | 십각형 프리즘 | 헨드각 프리즘 | 도십각 프리즘 | ... | 아페이로곤 프리즘 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 다면체 이미지 | ... | ||||||||||||
| 구형 타일링 영상 | 평면 타일링 영상 | ||||||||||||
| 정점 구성. | 2.4.4 | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | ... | ∞.4.4 |
| 콕시터 다이어그램 | ... |
참조
- ^ a b Pugh, Anthony (1976), Polyhedra: A Visual Approach, University of California Press, pp. 21, 27, 62, ISBN 9780520030565.
- ^ Simpson, Audrey (2011), Core Mathematics for Cambridge IGCSE, Cambridge University Press, pp. 266–267, ISBN 9780521727921.
- ^ Wheater, Carolyn C. (2007), Geometry, Career Press, pp. 236–237, ISBN 9781564149367.
외부 링크
- 3-Space VRML 모델의 균일한 Honeycombs
- 균일 폴리헤드라
- 가상현실 폴리헤드라 폴리헤드라 프리즘과 반격의 백과사전
- Weisstein, Eric W. "Hexagonal prism". MathWorld.
- 육각 프리즘 대화형 모델 - 웹 브라우저에서 작동 가능






