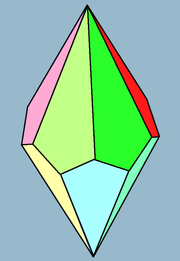
육각 사다리꼴

육각 사다리꼴
유형	사다리꼴 모양의
콘웨이	da6
콕시터 다이어그램
얼굴	연 12개
가장자리	24
정점	14
면 구성	V6.3.3.3
대칭군	D6d, [2+,12], (2*6), 주문 24
회전군	D6, [2,6],+ (66) 주문 12
이중 다면체	육각 항정신병
특성.	볼록한, 얼굴-변형

기하학에서 육각 사다리꼴 또는 델토헤드론은 대척점에 이중 다면체인 사다리꼴 무한 시리즈 중 네 번째다. 그것은 합성한 연인 열두 개의 얼굴을 가지고 있다.

그것은 등면체형이며, (얼굴-변환형) 모든 얼굴을 동일시한다. 보다 구체적으로 말하면, 모든 얼굴은 단순히 일치할 뿐 아니라 전이적이어야 한다. 즉, 동일한 대칭 궤도 내에 있어야 한다. 볼록한 등면체 다면체는 공정한 주사위를 만들 형상이다.^[1]

대칭

육각 사다리꼴의 대칭은 순서 24의 D이다_6d. 회전 그룹은 순서 12의 D이다₆.

변형

D₆ 대칭 내에서 1도의 자유도는 연을 3개의 가장자리 길이를 가진 합동 사분면 측정법으로 바꾼다. 한계에서, 각 사각형의 한쪽 가장자리는 길이가 0이 되고, 이것들은 두발자국이 된다.

원자의 결정 배열은 육각형 사다리꼴 세포로 우주에서 반복될 수 있다.^[2]

만약 두 봉우리를 둘러싸고 있는 연들이 다른 모양을 하고 있다면, 그것은 오직 C_6v 대칭, 순서 12를 가질 수 있다. 이것들은 불평등한 사다리꼴이라고 불릴 수 있다. 이중은 불평등한 항정신병이며, 위와 아래 폴리곤은 서로 다른 반경을 가지고 있다. 만약 그것이 뒤틀리고 불균등하다면, 그것의 대칭은 주기적인 대칭인₆ C 대칭으로 감소한다, 순서 6.

변동 예

유형	꼬임 사다리꼴(소면)		불평등사다리꼴레드라	불평등과 뒤틀림
대칭	D6, (662), [6,2],+ 주문 12		C6v, (*66), [6], 주문 12	C6, (66), [6],+ 주문 6
이미지 (n=6)
그물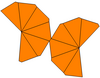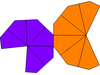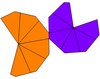

구면 타일링

육각형 사다리꼴도 역시 구형 타일링으로 존재하며, 극에 2개의 정점이 있고, 적도의 위아래에 일정한 간격을 두고 교대 정점이 있다.

관련 다면체

균일한 육각형 이면구형 다면체
대칭: [6,2], (*622)							[6,2]+, (622)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
듀얼 투 유니폼
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

n-곤 사다리꼴 헤드라 계열

사다리꼴 이름	디지온 사다리꼴 (테트라헤드론)	삼각 사다리꼴	사방형 사다리꼴	오각형 사다리꼴	육각 사다리꼴	십각형 사다리꼴	팔각사다리꼴	십각형 사다리꼴	도십각형 사다리꼴	...	아페이로겐 사다리꼴
다면체 이미지										...
구형 타일링 영상										평면 타일링 영상
면 구성	V2.3.3.3	V3.3.3.3	V4.3.3.3	V5.3.3.3	V6.3.3.3	V7.3.3.3	V8.3.3.3	V10.3.3.3	V12.3.3.3	...	V∞.3.3.3

참조

외부 링크

• Weisstein, Eric W. "Trapezohedron". MathWorld.
• 가상현실 폴리헤드라 폴리헤드라 백과사전
  • VRML 모델 <6>