IEEE 754

부동소수점 형식
IEEE 754
16비트: 절반(바이너리 16) 32비트: 싱글(2진수 32), 10진수 32 64비트: 이중(이진 64), 10진수 64 128비트: 4배(이진 128), 10진수 128 256비트: 10진수(바이너리256) 확장정밀도
다른.
미니플로트 bfloat 16 텐서플로트-32 마이크로소프트 바이너리 포맷 IBM 부동 소수점 아키텍처 PM버스 선형-11 G.7118-비트 플로트
대안
임의정밀도
v t

IEEE 표준 부동소수점 연산(IEEE 754)은 1985년 국제전기전자기술자협회(IEEE)가 제정한 부동소수점 연산의 기술표준입니다. 이 표준은 다양한 부동 소수점 구현에서 발견되는 많은 문제를 해결하여 안정적이고 휴대성 있게 사용하기 어려웠습니다. 많은 하드웨어 부동 소수점 장치는 IEEE 754 표준을 사용합니다.

이 표준은 다음을 정의합니다.

• 산술 형식: 이진 및 십진 부동 소수점 데이터 집합으로, 유한한 숫자(부호 0 및 하위 정규 숫자 포함), 무한 및 특수 "not a not a not a number" 값(NaNs)으로 구성됩니다.
• 교환 형식: 효율적이고 컴팩트한 형태로 부동 소수점 데이터를 교환하는 데 사용할 수 있는 인코딩(비트 문자열)
• 반올림 규칙 : 산술 및 변환 시 숫자 반올림 시 만족해야 할 속성
• 연산: 산술 형식에 대한 산술 및 기타 연산(삼각 함수 등)
• 예외처리 : 예외조건 표시(예를 들어 0으로 나누거나 넘침 등)

2008년 8월에 발표된 IEEE 754-2008은 거의 모든 원래 IEEE 754-1985 표준과 IEEE 854-1987 Radix-Independent 부동 소수점 산술 표준을 포함합니다. 현재 버전인 IEEE 754-2019는 2019년 7월에 출판되었습니다.^[1] 이전 버전을 약간 수정한 것으로, 주로 설명, 결함 수정 및 새로운 권장 작업이 포함되어 있습니다.

역사

부동 소수점 연산의 첫 번째 표준인 IEEE 754-1985는 1985년에 발표되었습니다. 이진 부동 소수점 산술만 다루었습니다.

새로운 버전인 IEEE 754-2008은 Dan Zuras가 의장을 맡고 Mike Cowlishaw가 편집한 7년간의 개정 과정을 거쳐 2008년 8월에 출판되었습니다. IEEE 754-1985 (이진 부동 소수점 산술)와 IEEE 854-1987 표준 for Radix-Independent 부동 소수점 산술을 모두 대체했습니다. 원래 표준의 이진 형식은 이진 형식 하나와 소수 형식 두 가지의 새로운 기본 형식과 함께 이 새로운 표준에 포함됩니다. 구현은 현재 표준을 준수하기 위해 기본 형식 중 하나 이상을 산술 형식과 교환 형식으로 구현해야 합니다.

국제 표준 ISO/IEC/IEEE 60559:2011(IEEE 754-2008과 동일한 내용)은 ISO/IEC JTC 1/SC 25를 통해 ISO/IEEE PSDO 협정에^[2][3] 따라 채택이 승인되어 공표되었습니다.^[4]

2019년 7월에 발표된 현재 버전인 IEEE 754-2019는 2015년 9월에 시작된 수정 프로세스에 따라 IEEE 754-2008에서 파생되었으며 이를 대체합니다. 마이크 코울리쇼가 편집했습니다. 여기에는 주로 설명(예: totalOrder)과 결함 수정(예: minNum)이 포함되어 있지만 몇 가지 새로운 권장 작업(예: 증강 추가)도 포함되어 있습니다.^[5][6]

국제표준 ISO/IEC 60559:2020(IEEE 754-2019와 동일한 내용의 ISO/IEC JTC 1/SC 25를 통해 채택이 승인되어 공표되었습니다.^[7]

다음으로 예상되는 표준 개정은 2028년입니다.^[8]

형식

IEEE 754 형식은 "수치와 기호의 표현 집합"입니다. 형식에는 세트가 인코딩되는 방법도 포함될 수 있습니다.^[9]

부동 소수점 형식은 다음과 같이 지정됩니다.

• IEEE 754에서 2(이진) 또는 10(십진) 중 하나인 베이스(라딕스라고도 함) b;
• 정밀도 p;
• 모든 IEEE 754 형식에 대해 emin = 1 - emax로 emin부터 emax까지 지수 범위를 나타냅니다.

형식은 다음과 같습니다.

• 세 개의 정수로 기술될 수 있는 유한한 숫자: s = 부호(0 또는 1), c = 유의어(또는 계수), 그리고 q = q + p - 1 ≤ emax가 되는 지수. 그런 유한한 숫자의 숫자 값은 (-1)^s × c × b입니다^q.^[a] 게다가 부호가 붙은 0이라고 불리는 두 개의 0 값이 있습니다. 부호 비트는 0이 +0(양의 0)인지 -0(음의 0)인지를 지정합니다.
• + ∞와 - ∞의 두 가지 무한대.
• 조용한 NaN(qNaN)과 신호 NaN(sNaN)의 두 종류의 NaN(not-a-number).

예를 들어, b = 10, p = 7, emax = 96인 경우, emin = -95인 경우, significand는 0 ≤ c ≤ 9999999를 만족하고, 지수는 -101 ≤ q ≤ 90을 만족합니다. 따라서 0이 아닌 최소의 양수는 1×10이고⁻¹⁰¹, 가장 큰 양수는 9999999×10⁹⁰(9.9999×10⁹⁶)이므로, 숫자의 전체 범위는 -9.9999×10⁹⁶~9.9999×10입니다⁹⁶. 숫자^1−emax -b와^1−emax b(여기서는 -1×10과⁻⁹⁵ 1×10⁻⁹⁵)가 가장 작은 정상 숫자입니다. 이 가장 작은 숫자들 사이의 0이 아닌 숫자를 정상이 아닌 숫자라고 합니다.

메모리에서의 표현 및 인코딩

일부 숫자에는 가능한 부동 소수점 표현이 여러 개 있을 수 있습니다. 예를 들어, b = 10이고 p = 7인 경우, -12.345는 -12345×10, -123450×10 및 -1234500×10으로 표현될 수 있습니다. 그러나 산술 연산과 같은 대부분의 연산에서 결과(값)는 입력의 표현에 의존하지 않습니다.

소수 형식의 경우 모든 표현이 유효하며 이러한 표현의 집합을 코호트라고 합니다. 결과가 여러 개의 표현을 가질 수 있는 경우 표준은 코호트의 어떤 구성원을 선택할 것인지를 지정합니다.

이진 형식의 경우 값을 정확하게 표현할 수 있도록 가장 작은 표현 가능한 지수를 선택하여 표현을 고유하게 만듭니다. 또한 지수를 직접적으로 표현하지는 않지만 가장 작은 대표 지수가 1로 표현되도록 편향이 추가되며, 0은 정상 이하의 숫자에 사용됩니다. 지수가 정규 범위에 있는 숫자의 경우(지수 필드가 모두 또는 모두 0이 아님), 유의 선행 비트는 항상 1이 됩니다. 따라서 메모리 인코딩에 명시적으로 존재하는 것이 아니라 선행 1이 암시될 수 있으며, 표준에 따르면 유의한 부분 중 명시적으로 표현되는 부분은 0과 1 사이에 있습니다. 이 규칙을 선행 비트 컨벤션, 암묵적 비트 컨벤션 또는 히든 비트 컨벤션이라고 합니다. 이 규칙을 사용하면 이진 형식이 추가적인 정밀도를 가질 수 있습니다. 선행 비트 규칙은 정규 지수 범위를 벗어난 지수와 가장 작은 정규 수에 사용되는 가장 작은 표현 지수에 의한 스케일을 가지므로 하위 정규 수에는 사용할 수 없습니다.

여러 인코딩(적어도 인터체인지 포맷이라고 불리는 형식)이 가능하기 때문에, NaN은 다른 정보를 운반할 수 있습니다: 부호 비트(의미는 없지만 일부 작업에 의해 사용될 수 있음)와 페이로드(payload). 이는 NaN의 소스를 나타내는 진단 정보를 위한 것입니다(그러나 페이로드에는 NaN-boxing과^[10][11][12] 같은 다른 용도가 있을 수 있음).

기본 및 교환 형식

이 표준은 숫자 베이스와 교환 인코딩에 사용되는 비트 수에 따라 명명된 5가지 기본 형식을 정의합니다. 3개의 이진 부동 소수점 기본 포맷(32, 64 또는 128비트로 인코딩됨)과 2개의 소수점 부동 소수점 기본 포맷(64 또는 128비트로 인코딩됨)이 있습니다. 바이너리 32 및 바이너리 64 형식은 각각 IEEE 754-1985의 단일 및 이중 형식입니다. 적합한 구현은 기본 형식 중 하나 이상을 완전히 구현해야 합니다.

표준은 또한 이러한 기본 형식을 일반화하는 교환 형식을 정의합니다.^[13] 이진 형식의 경우 선행 비트 규칙이 필요합니다. 다음 표는 가능한 몇 가지 교환 형식(기본 형식 포함)을 요약한 것입니다.

			유의와		지수		속성[b]
이름.	통칭	라딕스	자리수[c]	십진수[d]	분	맥스.	MAXVAL	로그10 MAXVAL	MINVAL>0(정상)	MINVAL>0(하위 규범)	메모들
바이너리 16	반정밀도	2	11	3.31	−14	15	65504	4.816	6.10·10−5	5.96·10−8	인터체인지
이진수 32	단일 정밀도	2	24	7.22	−126	+127	3.40·1038	38.532	1.18·10−38	1.40·10−45	기본의
바이너리64	2배 정밀도	2	53	15.95	−1022	+1023	1.80·10308	308.255	2.23·10−308	4.94·10−324	기본의
이진수 128	4배 정밀도	2	113	34.02	−16382	+16383	1.19·104932	4932.075	3.36·10−4932	6.48·10−4966	기본의
이진수256	10배 정밀도	2	237	71.34	−262142	+262143	1.61·1078913	78913.207	2.48·10−78913	2.25·10−78984	인터체인지
십진법 32		10	7	7	−95	+96	1.0·1097	97 − 4.34·10−8	1·10−95	1·10−101	인터체인지
십진수 64		10	16	16	−383	+384	1.0·10385	385 − 4.34·10−17	1·10−383	1·10−398	기본의
십진수 128		10	34	34	−6143	+6144	1.0·106145	6145 − 4.34·10−35	1·10−6143	1·10−6176	기본의

위의 표에서 정수 값은 정확한 반면, 십진법 표기의 as 값은 반올림된 값입니다(예: 1.0). 나열된 최소 지수는 정규 숫자에 대한 것입니다. 특수한 하위 정규 숫자 표현을 사용하면 더 작은(크기) 숫자도 어느 정도의 정밀도 손실과 함께 표현할 수 있습니다. 예를 들어, 이진 64에서 표현할 수 있는 최소 양수는 2이고, -1074 수치에 대한 기여는 -1022와 53개의 부호 및 비트 중 하나(2 = 2)를 제외한 모든 값을 포함합니다.

10진 숫자는 10진 숫자에 해당하는 숫자로 표현되는 형식의 정밀도입니다. 숫자 × 로그₁₀ 베이스로 계산됩니다. 예를 들어, 이진 128은 34자리 소수와 거의 동일한 정밀도를 갖습니다.

log₁₀ MAXVAL은 인코딩 범위의 척도입니다. 그 정수 부분은 과학 표기법에서 값의 출력에 표시되는 가장 큰 지수로, 소수점 이전에 앞자리가 하나 있습니다(예를 들어, 1.698·10은³⁸ 이진수 32에서 가장 큰 값 근처, 9.9999·10은⁹⁶ 십진수 32에서 가장 큰 값입니다).

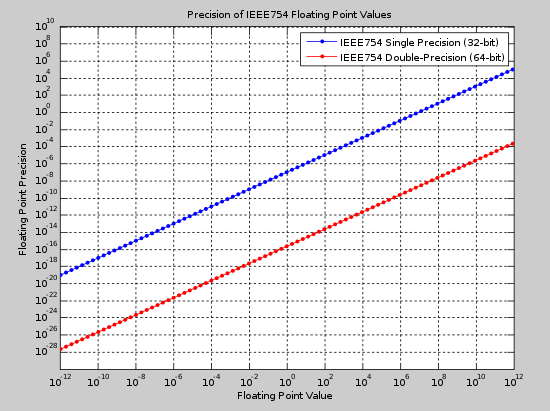
바이너리 32(단일) 및 바이너리 64(이중) 형식은 오늘날 가장 일반적으로 사용되는 두 가지 형식입니다. 아래 그림은 다양한 값 범위에서 두 형식 모두에 대한 절대 정밀도를 보여줍니다. 이 수치는 숫자의 예상 값과 필요한 정밀도를 고려하여 적절한 형식을 선택하는 데 사용할 수 있습니다.

32비트 부동 소수점 레이아웃의 예는 다음과 같습니다.

64비트 레이아웃도 비슷합니다.

확장 및 확장 가능한 정밀도 포맷

표준은 기본 형식보다 더 높은 정밀도를 제공하는 확장 및 확장 가능한 정밀도 형식을 선택적으로 지정합니다.^[14] 확장된 정밀도 형식은 더 정밀도와 더 지수적인 범위를 사용하여 기본 형식을 확장합니다. 확장 가능한 정밀도 형식을 사용하여 사용자가 정밀도 및 지수 범위를 지정할 수 있습니다. 구현은 이러한 형식에 대해 선택한 내부 표현을 사용할 수 있습니다. 정의해야 할 것은 매개 변수(b, p 및 emax)뿐입니다. 이러한 매개변수는 해당 매개변수가 나타낼 수 있는 유한한 수의 집합(지정된 래딕스에 대한 부호, 유의 및 지수의 조합)을 고유하게 설명합니다.

표준에서는 언어 표준에서 지원되는 각 기본 b에 대해 p 및 최대를 지정하는 방법을 제공할 것을 권장합니다.^[15] 표준에서는 언어 표준 및 구현이 각 radix b에 대해 지원되는 가장 큰 기본 형식보다 더 정확한 확장 형식을 지원할 것을 권장합니다.^[16] 두 기본 형식 사이의 정밀도를 갖는 확장 형식의 경우 지수 범위는 다음으로 넓은 기본 형식의 지수 범위와 같아야 합니다. 따라서 예를 들어 64비트 확장 정밀도 이진수는 최소 16383의 'emax'를 가져야 합니다. x87 80비트 확장 형식은 이 요구 사항을 충족합니다.

교환 형식

교환 형식은 주어진 형식에 대해 고정된 길이의 비트열을 사용하여 부동 소수점 데이터를 교환하기 위한 것입니다.

이진법

이진 부동 소수점 번호의 교환을 위해 길이 16비트, 32비트, 64비트 및 32비트 ≥ 128의 임의의 배수의 교환 형식이 정의됩니다. 16비트 형식은 작은 숫자(예: 그래픽용)의 교환 또는 저장을 위한 것입니다.

이러한 이진 교환 포맷의 인코딩 방식은 IEEE 754-1985의 인코딩 방식과 동일합니다: 부호 비트, 그 다음에 바이어스에 의한 지수 오프셋을 설명하는 w 지수 비트, 그리고 유의 부호를 설명하는 p - 1 비트. k-비트 형식에 대한 지수 필드의 폭은 w = round(4 log(k)) - 13으로 계산됩니다. 기존의 64비트 및 128비트 형식은 이 규칙을 따르지만 16비트 및 32비트 형식은 이 공식이 제공하는 것보다 지수 비트(각각 5 및 8)가 더 많습니다(각각 3 및 7).

IEEE 754-1985와 마찬가지로 바이어스-expon엔트 필드는 무한대(trailing 유의 및 필드 = 0) 또는 NaN(trailing 유의 및 필드 ≠ 0)을 나타내기 위해 모두 1비트로 채워집니다. NaNs의 경우, 조용한 NaNs와 시그널링 NaNs는 후행 significant 필드의 가장 중요한 비트를 독점적으로 사용하여 구별되며 ^[f]페이로드는 나머지 비트로 운반됩니다.

십진법

소수 부동 소수점 숫자의 교환을 위해 32비트의 임의의 배수의 교환 형식이 정의됩니다. 이진 인터체인지와 마찬가지로 십진 인터체인지 형식의 인코딩 체계는 부호, 지수 및 유의 부호를 인코딩합니다. 두 개의 서로 다른 비트 레벨 인코딩이 정의되며, 사용 중인 인코딩의 일부 외부 지표가 필요할 수 있다는 사실로 인해 상호 교환이 복잡합니다.

두 가지 옵션을 사용하면 significand를 조밀하게 채워진 10진수를 사용하여 10진수의 압축된 시퀀스로 인코딩하거나 이진 정수로 인코딩할 수 있습니다. 전자는 표준의 직접 하드웨어 구현에 더 편리하고 후자는 이진 컴퓨터의 소프트웨어 에뮬레이션에 더 적합합니다. 어느 경우든 인코딩 가능한 숫자(부호, 유의 및 지수의 조합)의 집합은 동일하며, 특수 값(최소 지수를 갖는 ±0, ±무한, 조용한 NaNs 및 신호 NaNs)은 동일한 인코딩을 갖습니다.

반올림 규칙

표준은 5개의 반올림 규칙을 정의합니다. 처음 두 규칙은 가장 가까운 값으로 반올림하고, 나머지 규칙은 지시된 반올림이라고 합니다.

가장 가까운 반올림

• 반올림 - 가장 가까운 값으로 반올림 - 가장 가까운 값으로 반올림합니다. 만약 숫자가 중간에 떨어지면, 그 숫자는 가장 작은 자릿수로 반올림됩니다.
• 가장 가까운 값으로 반올림합니다. 0에서 가장 가까운 값으로 반올림합니다(또는 0에서 먼 값으로 반올림). 숫자가 중간에 해당하는 경우 위(양의 숫자의 경우) 또는 아래(음의 숫자의 경우)로 반올림합니다.

극단에서 크기가 $k$ = ${\displaystyle {\text{최대}}^{}b}$- ${\displaystyle \frac{12}{}}$ b ${\displaystyle 1^{}}$- ${\displaystyle p^{}}$ ${\displaystyle$k =$b^{\text{emax}}\left(b-{\tfrac {1}{2}}b^{1-p}\right)}$보다 엄격하게 작은 값은 최소 또는 최대 유한 수(값 부호의 depending)로 반올림됩니다. 정확히 이 크기를 가진 모든 숫자는 타이로 간주되며, 이 타이 선택은${\displaystyle }$± ${\displaystyle {\text{최대}}^{}b}$- ${\displaystyle {b\mathrm{}}^{}}$ ${\displaystyle 1^{}}$- p${\displaystyle {}^{}}$ ${\display$ style $\pm$ b$^{\text{emax}}(b$ - b$^{1-p})}$ 및$$${\displaystyle }$± ${\displaystyle {\text{최대}}^{}}$+ ${\displaystyle 1^{}}$ ${\$ style $\pm$ b$^{\text{emax}}+1}$ 사이의 중간 지점으로 개념화될 수 있습니다$.$ 이 지수는 제한되지 않습니다. 크기가 더 큰 다음 대표 가능한 부동 소수점 숫자가 될 것입니다. 크기가 엄밀하게 k보다 큰 숫자는 해당 무한대로 반올림됩니다.^[17]

"가장 가까운 곳으로 반올림, 짝수로 연결"은 이진 부동 소수점의 기본값이며 십진법의 권장 기본값입니다. "가장 가까운 곳으로 반올림, 가까운 곳으로 연결"은 소수 구현에만 필요합니다.^[18]

방향 반올림

• 0을 향해 반올림 – 0을 향해 반올림(절단이라고도 함).
• + ∞을 향해 반올림 – 양의 무한대(반올림 또는 천장)를 향해 반올림합니다.
• 반올림 - ∞ – 음의 무한대(아래로 반올림 또는 바닥으로 반올림)를 향합니다.

IEEE 754 규칙을 사용한 정수 반올림 예

모드	예제값
	+11.5	+12.5	−11.5	−12.5
가장 가까운, 짝수의 관계	+12.0	+12.0	−12.0	−12.0
가장 가까운, 0에서 떨어진 넥타이	+12.0	+13.0	−12.0	−13.0
0을 향해	+11.0	+12.0	−11.0	−12.0
+ ∞ 쪽으로	+12.0	+13.0	−11.0	−12.0
∞을 향하여	+11.0	+12.0	−12.0	−13.0

달리 명시되지 않는 한 연산의 부동 소수점 결과는 무한히 정확한(수학적) 결과에 반올림 함수를 적용하여 결정됩니다. 이와 같은 동작은 정확하게 반올림된다고 합니다. 이 요구 사항을 올바른 반올림이라고 합니다.^[19]

필요한 작업

지원되는 산술 형식(기본 형식 포함)에 필요한 작업은 다음과 같습니다.

• 정수로^[20][21] 및 정수로 변환
• 이전 및 다음 연속^[20] 값
• 산술 연산(추가, 뺄셈, 곱셈, 나눗셈, 제곱근, 융합 곱셈, 나머지, 최소, 최대값)^[20][21]
• 변환(형식 간, 문자열 간 및 문자열 간 등)^[22][23]
• 스케일링 및 (십진법의 경우) 양자화^[24][25]
• 표지판(abs, negate 등)^[26]의 복사 및 조작
• 비교 및 총 주문^[27][28]
• 수(비정상, 유한 등) 분류 및 NaNs^[29] 시험
• 상태 플래그^[30] 테스트 및 설정

비교 술어

이 표준은 하나의 부동 소수점 데이터를 지원되는 산술 형식의 다른 부동 소수점 데이터와 비교하기 위한 비교 술어를 제공합니다.^[31] NaN과의 비교는 순서가 없는 것으로 처리됩니다. -0과 +0은 동일한 것으로 비교합니다.

총순서 술어

표준은 지원되는 산술 형식의 표준 멤버에 대한 총 순서를 정의하는 술어 Total Order를 제공합니다.^[32] 술어는 하나의 부동 소수점 숫자가 다른 숫자보다 작을 때 비교 술어(섹션 § 비교 술어 참조)와 일치합니다. 주요 차이점은 다음과 같습니다.^[33]

• NaN은 분류 가능합니다.
  • NaN은 Infinity(또는 다른 부동 소수점 숫자)보다 큰 절대값을 가지는 것처럼 취급됩니다. (-NaN < -Infinity; +Infinity < +NaN)
  • qNaN과 sNaN은 sNaN보다 qNaN이 절대값이 큰 것처럼 취급됩니다. (-qNaN < -sNaN; +sNaN < +qNaN.)
  • 그런 다음 NaN은 페이로드에 따라 정렬됩니다. IEEE 754-2008에서 페이로드가 작은 NaN은 절대값이 작은 것으로 취급됩니다. IEEE 754-2019에서는 모든 구현 정의 순서가 허용됩니다.
• 음수 0은 양수 0보다 작은 값으로 처리됩니다.
• 비교의 양쪽이 동일한 부동 소수점 기준을 참조하는 경우 지수가 작은 쪽이 절대값이 작은 것으로 처리됩니다.^[32]

totalOrder 술어는 형식의 모든 인코딩에 totalOrder를 부과하지 않습니다. 특히 하나 또는 둘 다 비표준 인코딩인 경우처럼 동일한 부동 소수점 표현의 서로 다른 인코딩 간에 구별되지 않습니다.^[32] IEEE 754-2019는 Total Order의 설명을 통합합니다.

부호화가 NaN 신호 비트 배치에 관한 IEEE 754-2008 권장사항을 따르는 이진 교환 형식의 경우, 비교는 부동 소수점 숫자를 부호 크기 정수(이 비교와 일치하는 페이로드 순서로 가정)로 입력하는 것과 동일하며, 이는 FPU가 없는 FP 비교를 위한 오래된 트릭입니다.^[34]

예외처리

이 표준은 5개의 예외를 정의하며, 각 예외는 기본값을 반환하고 예외가 발생할 때 해당 상태 플래그가 표시됩니다.^[g] 다른 예외 처리는 필요하지 않지만 기본값이 아닌 다른 대안을 추가로 사용하는 것이 좋습니다(§ 대체 예외 처리 참조).

5가지 가능한 예외는

• 잘못된 연산: 수학적으로 정의되지 않았습니다. 예를 들어 음수의 제곱근. 기본적으로 qNaN을 반환합니다.
• 0으로 나누기: 유한 피연산자에 대한 연산은 1/0 또는 log(0)과 같은 정확한 무한 결과를 제공합니다. 기본적으로 ±infinity를 반환합니다.
• 오버플로: 유한한 결과가 너무 커서 정확하게 표현할 수 없습니다(즉, 무한 지수 범위를 가진 지수는 emax보다 큽니다). 기본적으로 라운드 모드에서 가장 가까운 모드에 대해 ±infinity를 반환합니다(그리고 지시된 반올림 모드에 대한 반올림 규칙을 따릅니다).
• 언더플로우: 결과가 매우 작습니다(정상 범위를 벗어남). 기본적으로 는 최소 양수 정상 수보다 작거나 같은 수를 반환합니다(반올림 규칙에 따라). 하위 정상 수는 항상 언더플로우 예외를 의미하지만, 기본적으로 정확한 경우 플래그가 상승하지 않습니다.
• 부정확: 정확한(즉, 반올림되지 않은) 결과는 정확하게 표현할 수 없습니다. 기본적으로 정확하게 반올림한 결과를 반환합니다.

이들은 IEEE 754-1985에 정의된 것과 동일한 5가지 예외이지만, 0 예외에 의한 분할은 분할 이외의 작업으로 확장되었습니다.

일부 소수 부동 소수점 구현은 IEEE 754의 일부가 아닌 추가 예외를 정의합니다.^[35][36]

• 클램프됨: 결과의 지수가 대상 형식에 비해 너무 큽니다. 기본적으로 사용 가능한 가장 큰 값으로 지수를 줄이기 위해 후행 0이 계수에 추가됩니다. 이것이 불가능한 경우(이로 인해 필요한 자릿수가 대상 형식보다 많아야 하기 때문에) 오버플로 예외가 발생합니다.
• 반올림: 결과의 계수는 대상 형식이 제공하는 숫자보다 더 많은 숫자가 필요합니다. 0이 아닌 숫자가 폐기되는 경우 정확하지 않은 예외가 표시됩니다.

또한 피연산자 중 하나가 무한대인 경우 또는 결과가 대상 형식에 맞지 않는 경우 양자화와 같은 작업도 잘못된 작업 예외를 나타냅니다.^[37]

특수값

부호 0

IEEE 754 표준에서 0은 부호로 표시되며, 이는 "양의 0"(+0)과 "음의 0"(-0)이 모두 존재함을 의미합니다. 대부분의 런타임 환경에서 양의 0은 일반적으로 "로 인쇄됩니다.0" 그리고 음의 0은 ""로 표시됩니다.-0". 수치 비교에서는 두 값이 동일하게 작동하지만, 일부 작업에서는 +0과 -0에 대해 다른 결과를 반환합니다. 예를 들어, 1/(-0)은 음의 무한대를 반환하고, 1/(+0)은 양의 무한대를 반환합니다(아이덴티티 1/(1/±∞) = ±∞이 유지되도록 함). +0과 -0을 다르게 취급할 수 있는 x=0의 불연속성을 갖는 다른 일반적인 함수로는 로그(x), 부호(x), 음수 y에 대한 y + xi의 주 제곱근이 있습니다. 다른 근사 방식과 마찬가지로 "음의 0"과 관련된 작업은 때때로 혼동을 일으킬 수 있습니다. 예를 들어, IEEE 754에서 x = y는 항상 0 = -0과 같이 1/x = 1/y를 의미하는 것이 아니라 1/0 ≠ 1/(-0)을 의미합니다.

비정상수

하위 정규 값은 언더플로 갭 바로 바깥에 있는 인접 값과 절대 거리가 동일한 값으로 언더플로 갭을 채웁니다. 이는 언더플로우 갭이 0이고 언더플로우 결과가 0(flush to 0)으로 대체되는 기존 방식에 비해 개선된 것입니다.^[39]

최신 부동 소수점 하드웨어는 일반적으로 (정상 값뿐만 아니라) 하위 정규 값을 처리하며 하위 정규 값에 대한 소프트웨어 에뮬레이션을 필요로 하지 않습니다.

무한대

확장된 실수선의 무한대는 1, 1.5 등과 같은 일반적인 부동 소수점 값과 마찬가지로 IEEE 부동 소수점 데이터 유형으로 나타낼 수 있습니다. 오버플로가 있을 때 대체 값으로 사용되는 경우가 많지만(반올림에 따라 다름) 오류 값은 아닙니다. 0으로 나누는 예외의 경우 양 또는 음의 무한대가 정확한 결과로 반환됩니다. 무한은 숫자로 도입될 수도 있습니다(예를 들어 C의 "INFINITY" 매크로 또는 프로그래밍 언어가 해당 구문을 허용하는 경우 "∞").

IEEE 754는 다음과 같은 합리적인 방법으로 무한을 처리할 것을 요구합니다.

• (+∞) + (+7) = (+∞)
• (+∞) × (−2) = (−∞)
• (+∞) × 0 = NaN – 의미 있는 작업이 없습니다.

NaNs

IEEE 754는 0/0, ∞×0 또는 sqrt(-1)과 같은 특정 "무효" 연산의 결과로 반환되는 "NaN(Not a Number)"이라는 특별한 값을 지정합니다. 일반적으로, NaNs는 전파될 것입니다. 즉, NaN을 포함하는 대부분의 작업은 NaN을 초래할 것이지만, 주어진 부동 소수점 값에 대해 정의된 결과를 제공하는 함수는 NaN에 대해서도 그렇게 할 것입니다(예: NaN^ 0 = 1). NaNs에는 기본 조용한 NaNs와 선택적으로 신호를 보내는 NaNs의 두 가지가 있습니다. 임의의 산술 연산(수치 비교 포함)에서 신호 NaN은 "비활성 연산" 예외를 신호합니다.

표준에서 지정한 NaNs 표현에는 오류 유형 또는 소스를 인코딩하는 데 사용할 수 있는 지정되지 않은 비트가 있지만 해당 인코딩에 대한 표준은 없습니다. 이론적으로, 신호 NaNs는 런타임 시스템에서 초기화되지 않은 변수를 플래그로 표시하거나, 일반 값으로 계산 속도를 늦추지 않고 다른 특수 값으로 부동 소수점 수를 확장하는 데 사용될 수 있지만, 이러한 확장은 일반적이지 않습니다.

설계 근거

여기서 논의되는 IEEE 754 표준의 더 난해한 특징들, 예를 들어 확장 포맷, NaN, 무한대, 서브노멀 등은 수치 분석가에게만 관심을 갖거나 고급 수치 애플리케이션에만 관심을 갖는 것은 일반적인 오해입니다. 사실은 반대입니다. 이러한 기능은 전문가에 의해 정교한 수치 라이브러리를 지원할 뿐만 아니라 수치적으로 정교하지 않은 프로그래머에게 안전한 강력한 기본값을 제공하도록 설계되었습니다. IEEE 754의 핵심 설계자인 William Kahan은 "..."가 잘못되었다고 지적합니다. [deem] 2진 부동 소수점 연산을 위한 IEEE 표준 754의 특징은 다음과 같습니다.수치 전문가 외에는 아무도 사용할 수 없는 기능으로 인식되지 않습니다. 사실은 정반대입니다. 1977년에 이러한 기능들은 가능한 한 가장 넓은 시장을 제공하기 위해 인텔 8087로 설계되었습니다... 오류 분석은 IEEE 표준 754와 같은 부동 소수점 산술을 프로그래머들 사이의 선의의 무지에 적당히 관대하게 설계하는 방법을 알려줍니다."^[40]

• 무한대 및 NaN과 같은 특별한 값은 부동 소수점 연산이 대수적으로 완전함을 보장합니다. 모든 부동 소수점 연산은 잘 정의된 결과를 생성하며 기본적으로 기계 인터럽트 또는 트랩을 던지지 않습니다. 또한 예외적인 경우에 반환되는 특별한 값의 선택은 많은 경우에 정답을 제시하도록 설계되었습니다. 예를 들어, IEEE 754 산술 하에서 R(z):= 7 - 3/[z - 2 - 1/(z - 7 + 10/[z - 2 - 2/(z - 3))]와 같은 연속 분수는 모든 입력에서 정답을 제공할 것입니다. 예를 들어 z = 3의 경우 전위를 0으로 나눈 값은 + infinity로 올바르게 처리되므로 이러한 예외는 안전하게 무시할 수 있습니다. Kahan이 언급한 바와 같이, Ariane 5 로켓의 손실을 야기한 부동 소수점에서 16비트 정수 변환 오버플로에 대한 처리되지 않은 트랩은 기본 IEEE 754 부동 소수점 정책 하에서는 발생하지 않았을 것입니다.^[40]
• 정규 이하의 숫자는 유한 부동 소수점 숫자 x 및 y에 대해 x - y = y인 경우에만 x = 0이 되도록 보장하지만 이전 부동 소수점 표현에서는 성립하지 않습니다.
• x87 80비트 형식의 설계 근거에 대해 Kahan은 다음과 같이 언급합니다. "이 확장 형식은 속도 손실을 무시할 수 있을 정도로, 플로트와 이중 피연산자가 있는 가장 단순한 산술에 사용되도록 설계되었습니다. 예를 들어 다항식 평가, 스칼라 곱, 부분 및 연속 분수와 같은 반복을 구현하는 루프의 스크래치 변수에 사용해야 합니다. 단순 알고리즘을 망칠 수 있는 조기 오버/언더플로우 또는 심각한 로컬 취소를 방지하는 경우가 많습니다."^[43] 높은 정밀도와 확장 지수를 가진 확장된 형식의 중간 결과를 계산하는 것은 과학 계산의 역사적 관행과 과학 계산기의 설계에서 전례가 있습니다. Hewlett-Packard의 재무 계산기는 저장하거나 표시하는 것보다 더 중요한 세 소수까지 산술 및 재무 기능을 수행했습니다.^[43] 확장된 정밀도를 구현함으로써 일반적으로 한 단위(ULP) 내에서 고속으로 두 배의 정밀도 결과를 제공하는 표준 기본 기능 라이브러리를 쉽게 개발할 수 있었습니다.
• 값을 가장 가까운 대표 가능한 값으로 올바르게 반올림하면 계산에서 체계적인 편향이 방지되고 오류가 증가하는 속도가 느려집니다. 반올림 관계는 유사한 수치를 추가할 때 발생할 수 있는 통계적 편향을 제거합니다.
• 지시된 반올림은 예를 들어 인터벌 산술에서 오류 경계를 검사하는 데 도움이 되는 것으로 의도되었습니다. 일부 기능의 구현에도 사용됩니다.
• 연산의 수학적 기초, 특히 올바른 반올림을 통해 수학적 특성을 증명하고 2Sum, Fast2Sum 및 Kahan 합산 알고리즘과 같은 부동 소수점 알고리즘을 설계하여 정확도를 향상시키거나 다중 정밀 산술 서브루틴을 비교적 쉽게 구현할 수 있습니다.

단일 및 이중 정밀 포맷의 특성은 비트가 부호 크기의 정수를 나타내는 것처럼 부동 소수점 하드웨어를 사용하지 않고도 쉽게 정렬할 수 있다는 것입니다. 이것이 설계 고려 사항인지는 확실하지 않지만(이전 IBM 16진수 부동 소수점 표현에도 정규화된 숫자에 대한 이러한 속성이 있었다는 점은 주목할 만하다). 일반적인 두 개의 보어 표현에서는 비트를 부호가 붙은 정수로 해석하면 양수가 올바르게 정렬되지만 음수는 반대로 정렬됩니다. 이에 대한 한 가지 가능한 수정으로 x 또는 부호 비트를 양의 값으로, 모든 비트를 음의 값으로 뒤집으면 모든 값이 부호가 없는 정수로 정렬됩니다(-0 < +0 포함).^[34]

추천 사항

대체 예외 처리

이 표준은 사용자 정의 기본값의 대체, 트랩(어떤 방식으로든 제어 흐름을 변경하는 예외) 및 흐름을 방해하는 다른 예외 처리 모델(예: 시도/캐치)을 포함한 다양한 형태의 선택적 예외 처리를 권장합니다. 트랩 및 기타 예외 메커니즘은 IEEE 754-1985에서와 같이 옵션으로 유지됩니다.

권장 작업

표준의 9항은 언어 표준이 정의해야 할 추가적인 수학 연산을^[44] 권장합니다.^[45] 표준을 준수하기 위해 필요하지 않습니다.

올바르게 반올림해야 하는 권장 산술 연산은 다음과 같습니다.^[46]

• ${\displaystyle x^{}}$ ${\$ 2 ${\displaystyle x^{}}$ ${\$ ${\displaystyle {10}^{}}$ x ${\$
• ${\displaystyle {}^{}\mathrm{x}{}^{}}$- 1 ${\displaystyle e^{x}-1$ ${\displaystyle 2^{}}$ $x{\displaystyle {\mathrm{}}^{}}$- ${\displaystyle 1}$ ${\displaystyle 2^{x}-1$ ${\displaystyle {10}^{}}$ ${\displaystyle \mathrm{x}{}^{}}$- 1 ${\displaystyle 10^{x}-1}$
• $ln ⁡$ x {\$displaystyle$${\displaystyle {\ln }_{}}$ ${\displaystyle x_{}}$ ${\displaystyle 로}$${\displaystyle 그}$$2$ ⁡ x${\displaystyle$ $\backslash$${\displaystyle {\log }_{}}$_{${\displaystyle 2}$}x$},$ $로그$${\displaystyle }$$10$ ⁡$x {\displaystyle$ \log _{10}x}
• ${\displaystyle \ln }$$⁡($1 $+$ x) {\$displaystyle$\ln$($${\displaystyle 1_{}}$ + x${\displaystyle {}_{}\mathrm{로}}$${\displaystyle 그}$${\displaystyle 2}$ ⁡(1 + x$) {\displaystyle$${\displaystyle {\log }_{}}$ _{${\displaystyle 2_{}}$1${\displaystyle }$+ $x$${\displaystyle }$$10$ ⁡($1$+ x)${\displaystyle$ \log _{10}(1 + x)}
• ${\textstyle {\sqrt {x^{2}+y^{2}}}}$
• ${\displaystyle 1{\big /}{\sqrt {x{\vphantom {t}}}}$
• ${\displaystyle (1}$+ x${\displaystyle {}^{})}$ ${\displaystyle \mathrm{x}}$ $≥$ - 1${\displaystyle$x\geq -1}에 대한 n ${\displaystyle (1$+ $x)^{n}($화합물 이름을 지정하고 지수 증가를 계산하는 데 사용되며 비율은 -1보다 작을 수 없음)
• ${\displaystyle x^{\frac {1}{n}}$
• ${\displaystyle {xn}^{}}$ ${\$ $x$$^{n$ ${\displaystyle {xy}^{}}$ ${\$ x$^{y}$
• $in ⁡$ x ${\displaystyle$${\displaystyle \sin }$ x${\displaystyle \},}$${\displaystyle c}$$os$$⁡$ x {\${\displaystyle \mathrm{displaystyle}}$ \${\displaystyle \cos }$x}, ${\displaystyle t}$$an$ ⁡$$x {\displaystyle \tan x}
• ${\displaystyle \arcsin x}$, ${\displaystyle \arccos x}$, ${\displaystyle \arctan x}$, ${\displaystyle \operatorname {atan2} (y,x)}$
• ${\displaystyle \mathrm{si}n\mathrm{Pi}}$ ${\displaystyle }$ ${\displaystyle x}$ $=$ ${\displaystyle \sin }$⁡ $π$ x ${\displaystyle \operatorname$ {sinPi${\displaystyle \}}$ x =\${\displaystyle \sin }$ \pi${\displaystyle x}$}, co${\displaystyle s}$Pi ${\displaystyle }$ x ${\displaystyle =}$ ${\displaystyle \cos }$ ⁡ π x $displaystyle$ \$operatorname {cosPi$${\displaystyle \}}$ ${\displaystyle x}$ =\cos \${\displaystyle \mathrm{pi}}$ x${\displaystyle \},}$${\displaystyle n}$${\displaystyle \mathrm{Pi}}$ ${\displaystyle }$$$x$$=${\displaystyle \mathrm{ta}}$n⁡ π x {\$displaystyle \operatorname$ {tanPi${\displaystyle \}}$ x =\tan \pi x}( 참조). π의 배수)
• ${\displaystyle \mathrm{asi}n\mathrm{Pi}}$ ${\displaystyle }$ ${\displaystyle x}$ $=$$$$π$ arc${\displaystyle s}$in ⁡ x {\$display 스타일$\operatorname {$asinPi$x = {\$tfrac$ $\{$${\displaystyle 1}$} {\${\displaystyle \mathrm{pi}}$}}\arcsin ${\displaystyle x}$}, ${\displaystyle \mathrm{aco}}$${\displaystyle s}$${\displaystyle \mathrm{Pi}}$ ${\displaystyle }$ ${\displaystyle x}$ =$π ar$${\displaystyle c}$$os$ ⁡ x {\$display style$ \$operatorname${${\displaystyle \mathrm{acosPi}}$${\displaystyle \}}$${\displaystyle x}$ = {\${\displaystyle \frac{\mathrm{tfrac}}{}}$ {${\displaystyle 1}$} {\$}\arcos$ x }, ata${\displaystyle n}$Pi ${\displaystyle }$$$${\displaystyle x}$$$=$π arc$${\displaystyle t}$$an$ ⁡ x {\$display$ style \operatorname {atanPi${\displaystyle \}}$ x = {\tfac} ${\displaystyle \mathrm{atan}2\mathrm{Pi}(\frac{y}{}}$, ${\displaystyle x}$ ${\displaystyle )}$ $= π$ atan2Pi(y,$$x) ${\displaystyle \operatorname$ {$atan2Pi}($)={\tfrac ${1}{\pi}}}\operatorname$ {atan2}(y,x)}( 참조). π의 배수)
• ${\displaystyle si\mathrm{nh}}$ $⁡$ x${\displaystyle$${\displaystyle \sinh }$ x$c$${\displaystyle o}$$sh$ ⁡$x$$\{\backslash$${\displaystyle \mathrm{displaystyle}}$\${\displaystyle \cosh }$x}, $t$${\displaystyle a}$$nh$ ⁡$$x {\displaystyle \tanh x}
• ${\displaystyle \mathrm{arsinh}}$ $⁡$ $x$ {\displaystyle \$operatorname {arsinh$${\displaystyle x}$}, ${\displaystyle \mathrm{arc}}$${\displaystyle o}$$⁡$$$x ${\displaystyle$ \$operatorname$${\displaystyle \mathrm{arcosh}\}}$ $},$ $art$${\displaystyle a}$$nh ⁡$ x {\$displaystyle \operatorname$ {artanh} x}

${\displaystyle \mathrm{pi}}$ ${\displaystyle \operatorname {asinPi$ ${\displaystyle \mathrm{acosPi}}$ ${\displaystyle \operatorname {acosPi}$및$$ ${\displaystyle \mathrm{tanPi}}$ ${\displaystyle \operatorname {tanPi}$함수는$$ 덜 필요한 것으로 간주되어 IEEE 754-2008 표준에 포함되지 않았습니다.^[48] ${\displaystyle \mathrm{Pi}}$ ${\displaystyle \operatorname {asinPi}$및 ${\displaystyle \mathrm{acosPi}}$ ${\displaystyle \operatorname {acosPi}$이$($가) 언급되었지만 이는 오류로 간주되었습니다.^[5] 세 가지 모두 2019년 개정에서 추가되었습니다.

권장 작업에는 동적 모드 반올림 방향 설정 및 액세스,^[49] 표준에 의해 정확도가 지정되지 않은 합계, 스케일링된 제품, 점 제품과 같은 구현 정의 벡터 감소 작업도 포함됩니다.^[50]

2019년^[update] 현재 이진 형식에 대한 증강 산술 연산도^[51] 권장됩니다. 덧셈, 뺄셈 및 곱셈에 대해 지정된 이러한 작업은 형식에서 가장 가까운 값으로 정확하게 반올림된 결과와 형식에서 정확히 표현할 수 있는 오류 항으로 구성된 한 쌍의 값을 생성합니다. 표준을 발표할 당시에는 하드웨어 구현이 알려져 있지 않지만, 이미 잘 알려진 알고리즘을 사용하여 소프트웨어에서 매우 유사한 연산을 구현했습니다. 표준화의 역사와 동기는 배경 문서에 설명되어 있습니다.^[52][53]

IEEE 754-2008의 minNum, minNumMag 및 maxNumMag는 2019년 현재 비연동성 때문에 사용되지 않습니다. 대신 두 세트의 새로운 최소 및 최대 작업이 권장됩니다.^[54] 첫 번째 세트에는 minimum, minimum Number, maximum Number가 포함되어 있습니다. 두 번째 세트에는 최소 크기, 최소 크기 번호, 최대 크기 및 최대 크기 번호가 포함되어 있습니다. 이러한 변화의 역사와 동기는 배경 문서에 설명되어 있습니다.^[55]

표현평가

이 표준은 언어 표준이 연산 시퀀스의 의미를 지정하는 방법을 권장하고 결과 값을 변경하는 문자적 의미와 최적화의 미묘함을 지적합니다. 대조적으로, 이전 1985년 버전의 표준은 언어 인터페이스의 측면을 지정되지 않은 채로 남겨 두었고, 이로 인해 컴파일러 간에 일관되지 않은 동작이 발생하거나 최적화 컴파일러에서 다른 최적화 수준이 발생했습니다.

프로그래밍 언어는 사용자가 각 래딕스에 대한 표현식의 중간 계산을 위한 최소 정밀도를 지정할 수 있어야 합니다. 이를 표준에서 preferred Width라고 하며 블록 단위로 설정할 수 있어야 합니다. 식 내의 중간 계산을 계산하고 피연산자 폭의 최대값과 설정된 경우 선호하는 폭을 사용하여 임시를 저장해야 합니다. 따라서 예를 들어 x87 부동 소수점 하드웨어를 대상으로 하는 컴파일러는 중간 계산이 이중 확장 형식을 사용해야 함을 지정하는 수단을 가져야 합니다. 이후 식을 평가할 때는 반올림하고 변수에 할당하기 전의 전구체가 아니라 변수의 저장된 값을 항상 사용해야 합니다.

재현성

IEEE 754-1985 버전의 표준은 구현에서 많은 변형(예를 들어 일부 값의 인코딩 및 특정 예외 감지)을 허용했습니다. IEEE 754-2008은 이러한 허용치를 줄였지만, (특히 이진 형식의 경우) 여전히 몇 가지 변형이 남아 있습니다. 재현성 조항은 언어 표준이 재현 가능한 프로그램(즉, 언어의 모든 구현에서 동일한 결과를 생성하는 프로그램)을 작성할 수 있는 수단을 제공해야 한다고 권고하고 재현 가능한 결과를 달성하기 위해 수행해야 할 작업을 설명합니다.

문자 표현

이 표준에서는 기본 형식과 외부 문자 시퀀스 형식 간의 변환 작업이 필요합니다.^[56] 모든 형식에 대해 10진수 문자 형식으로 변환하거나 변환해야 합니다. 외부 문자 시퀀스로의 변환은 반올림에서 가장 가까운 것으로, 짝수에 대한 연결을 사용하여 다시 변환하면 원래 번호를 복구할 수 있습니다. 조용한 NaN 또는 시그널링 NaN의 페이로드를 보존할 필요가 없으며, 외부 문자 시퀀스로부터의 변환은 시그널링 NaN을 조용한 NaN으로 바꿀 수 있습니다.

원래 이진값은 다음을 사용하여 10진수로 변환하고 다시 되돌림으로써 보존됩니다.^[57]

• 이진법 16의 소수점 5자리,
• 이진수 32의 경우 10진수 9자리,
• 이진법 64의 경우 10진법 17자리,
• 이진수 128의 경우 10진수 36자리입니다.

다른 이진 형식의 경우 필요한 소수 자릿수는 다음과^[h] 같습니다.

${\displaystyle 1+\lceil p\log _{10}(2)\rceil,}$

여기서 p는 바이너리 형식의 중요한 비트 수(예: 바이너리 256의 경우 237 비트)입니다.

소수 부동 소수점 형식을 사용하는 경우 소수점 표현은 다음을 사용하여 보존됩니다.

• 10진수 32의 경우 10진수 7자리,
• 16진수 64,
• 12진수 128의 경우 34진수입니다.

이진법에서 십진법으로, 십진법에서 이진법으로 정확하게 반올림된 변환을 위한 알고리즘은 게이에 의해 ^[58]논의되고 테스트를 위해 팍슨과 케이한에 의해 논의됩니다.^[59]

16진법

이 표준은 C99의 16진수 부동 소수점 리터럴을 기반으로 외부 16진수-의미 및 문자 시퀀스에 대한 변환을 제공할 것을 권장합니다. 이러한 리터럴은 선택적인 기호로 구성됩니다.+ 또는 -), 기호 "0x", 마침표가 있거나 없는 16진수, 지수 표시자 "p", 옵션 기호가 있는 10진수 지수. 구문은 대소문자를 구분하지 않습니다.^[60] 십진 지수는 2의 거듭제곱으로 스케일링되므로, 예를 들어, 0x0.1p-4 256분의 1입니다.^[61]

참고 항목

• bfloat16 부동 소수점 형식
• 비네이드
• 코프로세서
• IEEE 754 기능의 액세스 및 사용을 보여주는 코드 예제용 C99
• IEEE 754 기능의 이력, 설계 근거 및 사용 예시를 위한 부동 소수점 산술
• 유리수를 사용한 계산에서 대안적인 접근 방식을 위한 고정점 산술(특히 지수 범위가 컴파일 시 알려지거나 고정되거나 바인딩될 때 유용함)
• IBM System z9, 최초로 IEEE 754-2008 10진법(하드웨어 마이크로코드 사용)을 구현한 CPU
• IBM z10, IBM z196, IBM zEC12 및 IBM z13, IEEE 754-2008 소수 연산을 하드웨어로 완벽하게 구현하는 CPU
• ISO/IEC 10967, 언어 독립 연산(LIA)
• IEEE 754 원칙에 따른 미니플로트, 저정밀 이진 부동 소수점 포맷
• 하드웨어로 IEEE 754-2008 소수 연산을 완벽하게 구현하는 POWER6, POWER7 및 POWER8 CPU
• strictfp는 자바 프로그래밍 언어에서 이전에 일반적인 하드웨어 플랫폼에서 재현성을 보장하기 위해 산술을 IEEE 754 단일 및 이중 정밀도로 제한했던 구식 키워드입니다(Java 17 기준으로 이 동작이 필요합니다).
• 함수의 정확한 반올림에 대한 테이블 메이커의 딜레마
• 표준 Apple Numerics 환경
• 테이퍼 부동소수점
• 대체 번호 형식인 Posit

메모들

참고문헌

표준

• IEEE Standard for Binary Floating-Point Arithmetic. ANSI/IEEE STD 754-1985. IEEE. 1985-10-12. pp. 1–20. doi:10.1109/IEEESTD.1985.82928. ISBN 0-7381-1165-1.
• IEEE Computer Society (2008-08-29). IEEE Standard for Floating-Point Arithmetic. IEEE STD 754-2008. IEEE. pp. 1–70. doi:10.1109/IEEESTD.2008.4610935. ISBN 978-0-7381-5753-5. IEEE Std 754-2008.
• IEEE Computer Society (2019-07-22). IEEE Standard for Floating-Point Arithmetic. IEEE STD 754-2019. IEEE. pp. 1–84. doi:10.1109/IEEESTD.2019.8766229. ISBN 978-1-5044-5924-2. IEEE Std 754-2019.
• ISO/IEC JTC 1/SC 25 (June 2011). ISO/IEC/IEEE 60559:2011 — Information technology — Microprocessor Systems — Floating-Point arithmetic. ISO. pp. 1–58.{{cite book}}: CS1 메인트: 숫자 이름: 작성자 목록(링크)
• ISO/IEC JTC 1/SC 25 (May 2020). ISO/IEC 60559:2020 — Information technology — Microprocessor Systems — Floating-Point arithmetic. ISO. pp. 1–74.{{cite book}}: CS1 메인트: 숫자 이름: 작성자 목록(링크)

2차 참조

• 소수 부동 소수점 산술, FAQ, 서지 및 링크
• 이진 플로트 비교
• IEEE 754 참조 자료
• IEEE 854-1987 – 역사와 분
• IEEE 754에 대한 보충 판독값. 역사적 관점을 포함합니다.

추가읽기

• Goldberg, David (March 1991). "What Every Computer Scientist Should Know About Floating-Point Arithmetic" (PDF). ACM Computing Surveys. 23 (1): 5–48. doi:10.1145/103162.103163. S2CID 222008826. Archived (PDF) from the original on 2006-07-20. Retrieved 2016-01-20. ([1], [2], [3])
• Hecker, Chris (February 1996). "Let's Get To The (Floating) Point" (PDF). Game Developer Magazine: 19–24. ISSN 1073-922X.
• Severance, Charles (March 1998). "IEEE 754: An Interview with William Kahan" (PDF). IEEE Computer. 31 (3): 114–115. doi:10.1109/MC.1998.660194. S2CID 33291145. Retrieved 2019-03-08.
• Cowlishaw, Mike (June 2003). "Decimal floating-point: Algorism for computers". 16th IEEE Symposium on Computer Arithmetic, 2003. Proceedings (PDF). Los Alamitos, Calif.: IEEE Computer Society. pp. 104–111. doi:10.1109/ARITH.2003.1207666. ISBN 978-0-7695-1894-7. S2CID 18713046. Retrieved 2014-11-14.Cowlishaw, Mike (June 2003). "Decimal floating-point: Algorism for computers". 16th IEEE Symposium on Computer Arithmetic, 2003. Proceedings (PDF). Los Alamitos, Calif.: IEEE Computer Society. pp. 104–111. doi:10.1109/ARITH.2003.1207666. ISBN 978-0-7695-1894-7. S2CID 18713046. Retrieved 2014-11-14.(주: 알고리즘은 제목의 철자를 잘못 쓴 것이 아닙니다. 알고리즘도 참조하십시오.)
• Monniaux, David (May 2008). "The pitfalls of verifying floating-point computations". ACM Transactions on Programming Languages and Systems. 30 (3): 1–41. arXiv:cs/0701192. doi:10.1145/1353445.1353446. ISSN 0164-0925. S2CID 218578808.인기 있는 아키텍처에 대한 부동 소수점의 비직관적 행동에 대한 Monniaux, David (May 2008). "The pitfalls of verifying floating-point computations". ACM Transactions on Programming Languages and Systems. 30 (3): 1–41. arXiv:cs/0701192. doi:10.1145/1353445.1353446. ISSN 0164-0925. S2CID 218578808.개요와 프로그램 검증 및 테스트에 대한 함의.
• Muller, Jean-Michel; Brunie, Nicolas; de Dinechin, Florent; Jeannerod, Claude-Pierre; Joldes, Mioara; Lefèvre, Vincent; Melquiond, Guillaume; Revol, Nathalie; Torres, Serge (2018) [2010]. Handbook of Floating-Point Arithmetic (2 ed.). Birkhäuser. doi:10.1007/978-3-319-76526-6. ISBN 978-3-319-76525-9.
• Overton, Michael L. (2001). Written at Courant Institute of Mathematical Sciences, New York University, New York, US. Numerical Computing with IEEE Floating Point Arithmetic (1 ed.). Philadelphia, US: SIAM. doi:10.1137/1.9780898718072. ISBN 978-0-89871-482-1. 978-0-89871-571-2, 0-89871-571-7.
• 부동 소수점 번호의 Cleve Moler
• Beebe, Nelson H. F. (2017-08-22). The Mathematical-Function Computation Handbook - Programming Using the MathCW Portable Software Library (1 ed.). Salt Lake City, UT, US: Springer International Publishing AG. doi:10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN 2017947446. S2CID 30244721.
• Hough, David G. (December 2019). "The IEEE Standard 754: One for the History Books". Computer. IEEE. 52 (12): 109–112. doi:10.1109/MC.2019.2926614. S2CID 208281213.

외부 링크

• Kahan on creating IEEE Standard Floating Point. Turing Awardee Clips. 2020-11-16. Archived from the original on 2021-11-08.
• 온라인 IEEE 754 이진 계산기