콜모고로프-주르벤코 필터

통계 정보 내에서 A가 최초로 제안한 것은 Kolmogorov-Zurbenko(KZ) 필터입니다.N. 콜모고로프이며 주르벤코에 ^[1]의해 공식적으로 정의되었습니다.길이 m의 이동 평균 필터의 일련의 반복입니다. 여기서 m은 양의 홀수 정수입니다.KZ 필터는 저역 통과 필터 클래스에 속합니다.KZ 필터에는 이동 평균 창의 길이 m과 이동 평균 자체의 반복 횟수 k라는 두 가지 매개변수가 있습니다.또한 스펙트럼 누출을 제거하기 위해 설계된 특수 윈도우 기능으로 간주할 수 있다.

안드레이 콜모고로프와 이고르 주르벤코가 태평양에서 연구선을 탔습니다.

배경

A. N. 콜모고로프는 태평양의 ^[1]난류를 연구하는 동안 KZ 필터에 대한 독창적인 아이디어를 가지고 있었다.콜모고로프는 난류의 에너지 스펙트럼에서 5/3의 법칙으로 국제 발잔상을 받았다.놀랍게도 태평양에서는 5/3법이 지켜지지 않아 큰 우려를 불러일으켰다.표준 FFT(Fast Fourier Transform)는 소음과 비정상 해양 환경에 완전히 속아 넘어갔습니다.KZ 필터링은 문제를 해결하고 해당 도메인에서 Kolmogorov의 법칙을 증명할 수 있도록 했습니다.필터 구성은 연속 푸리에 변환의 주요 개념과 그 이산적 유사점에 의존했습니다.KZ 필터의 알고리즘은 이산 함수의 고차 도함수의 정의에서 고차 차이의 정의에서 비롯되었습니다.가우스 창의 무한 평활성은 정말 이산적인 세계의 아름답지만 비현실적인 근사치라고 믿었던 콜모고로프는 유한한 지지대를 가진 미세하게 구별 가능한 테이퍼링 창을 선택했고 이산적인 ^[1]경우를 위한 이 수학적 구조를 만들었다.KZ 필터는 견고하고 거의 최적입니다.KZ 필터는 단순한 이동 평균(MA)이기 때문에 결측 데이터 환경, 특히 공간적 희박성으로 결측 데이터 문제가 발생하는 다차원 시계열에서 우수한 성능을 발휘합니다.KZ 필터의 또 다른 장점은 두 파라미터의 해석이 명확하여 서로 다른 분야의 전문가가 쉽게 채택할 수 있다는 것입니다.인기 있는 통계 소프트웨어 R에서는 시계열, 종방향 및 공간 데이터를 위한 몇 가지 소프트웨어 패키지가 개발되어 서로 다른 영역에서 KZ 필터와 그 확장을 쉽게 사용할 수 있다.Jerzy Neyman 및 Elizabeth Scott와 함께 UC Berkeley에서 I.Zurbenko 포스트닥터 직책은 Murray Rosenblatt, Robert Shumway, Harald Cramér, David Brillinger, Herbert Robins, Wilfrid Dixon, Emanuel Parzenko Parzenko와 함께 지원된 응용 프로그램에 대한 많은 아이디어를 제공했습니다.파젠, T.W.앤더슨 및 UC 버클리 통계학과.

정의.

KZ 필터

$\{X(t)\},t=0,\pm 1,\pm 2,\dots$ ( $\{X(t)\},t=0,\pm 1,\pm 2,\dots$ ) $\{X(t)\},t=0,\pm 1,\pm 2,\dots$ , $\{X(t)\},t=0,\pm 1,\pm 2,\dots$ $\{X(t)\},t=0,\pm 1,\pm 2,\dots$ , ± $\{X(t)\},t=0,\pm 1,\pm 2,\dots$ , ± $\{X(t)\},t=0,\pm 1,\pm 2,\dots$ , $...$ { $displaystyle$ \ { $X$ ( $t$ ) \ , t $\{X(t)\},t=0,\pm 1,\pm 2,\dots$ = $0$ , \ $pm$ 2, \ $display$ } ersers m series $}$ series series series {\ series series}、 m { $displaystyle$ m}및 $m$ $k$ { \ $displaystyle$ k}의 $\{X(t)\},t=0,\pm 1,\pm 2,\dots$ $k$ KZ 필터는 다음과 같이 정의됩니다.

KZ_{m,k}[X(t)]=\sum _{s=-k(m-1)/2}{X(t+s)\times {a_{m,k}}

여기서 계수는

{\displaystyle a_{s}^{m,k}=mfrac {c_{s}^{k,m}}{m^{k}},s=mfrac {-k(m-1)}{2}},\display,{\frac {k(m-1)

방정식에서 얻은 다항식 계수에 의해 주어지는

\displaystyle \sum _{r=0}^{k(m-1)}{z^{r}c_{r-k(m-1)/2}^{k,m}=(1+z+\display +z^{m-1})^{k}}}}

다른 관점에서 $파라미터$ m $\$ $displaystyle$ m $k$ k\ $displaystyle$ k를 $k$ $갖는$ KZ 필터는 m\displaystyle $m포인트$ 의 $m$ 이동평균( $MA$ ) 필터의 k $\$ $displaystyle$ k시간 $k$ 반복으로 $k$ 할 수 있습니다.반복을 통해 얻을 수 있습니다.

첫 번째 반복은 $X(t)$ X에 MA 필터를 적용하는 것입니다.( $X(t)$ ) { $displaystyle$ X $(t)}$

KZ_{m,k=1}[X(t)]=\sum_{s=-(m-1)/2}{X(t+s)}\times {1}{m}

두 번째 반복은 첫 번째 반복의 결과에 MA 연산을 적용하는 것입니다.

{begin}&KZ_{m,k=2}[X(t)]=\sum_{s=-(m-1)/2}{KZ_{m,k=1}[X(t+s)]\times {frac1}{m}\sum={sum

일반적으로 k번째 반복은 (k - 1)번째 반복에 대한 MA 필터의 적용입니다.MA의 간단한 조작의 반복 프로세스는 계산적으로 매우 편리합니다.

특성.

필터 곱의 임펄스 응답 함수는 임펄스 응답의 컨볼루션이다.KZ 필터의 계수는 k개의 균일한 이산 분포를 [ - ( $m -$ 1)/ $2 ,$ ( $m - 1$ )/ $2$ ] 구간에서곱한 분포로 해석할 수 있습니다.여기서 m은 홀수 정수입니다.따라서 $계수$ a는 유한한 지지 $[($ m- $1$ ) $k$ + 1 $]$ 를 갖는 테이퍼링 창을 형성합니다.KZ $필터$ a는 mµk $길이$ 에 집중된 주요 중량을 가지며 외부에서는 무게가 $0$ 으로 사라집니다.KZ 필터의 임펄스 응답 함수는 k - $2$ 연속 도함수를 $가지며$ 점근적으로 가우스 분포입니다.임펄스 응답 함수의 엣지에 0 도함수는 고주파 분해능에서 분해되는 급격한 감소 함수를 만듭니다.KZ 필터의 에너지 전달 기능은

B_{m,k}(\obe) ^{2}=\left\{\frac {1}{m}}{\frac {sin(\pi m\obe)}{\sin(\pi \obe)}}{\right\}^2k}

이 필터는 컷오프 빈도가 다음과 같은 로우패스 필터입니다.

{\displaystyle \mega _{0}\약 {\frac {1-(1/2)^{1/2k}}{m^{2}-(1/2)^{1/2k}}}}}}.

그림 1k = 1에 대한 필터 전달 함수.

MA 필터에 비해 KZ 필터는 컷오프 주파수 이상의 주파수 성분을 감쇠시키는 점에서 성능이 훨씬 우수합니다.KZ 필터는 기본적으로 반복 MA 필터입니다.계산하기 쉽고 누락된 데이터를 쉽게 처리할 수 있습니다.이 절차의 주요 내용은 구간 내 결측 관측치를 무시하고 m개 구간 내에서 사용 가능한 정보의 단순 평균입니다.동일한 아이디어를 공간 데이터 분석으로 쉽게 확장할 수 있습니다.결측치는 KZ 필터의 전송 기능에 거의 영향을 주지 않는 것으로 나타났습니다.

임의의 k는 이 전송 함수의 k의 전력을 제공하고 사이드 로브 값을 0 $.05$ 로^k 줄입니다.완벽한 로우패스 필터가 될 것입니다.통상적인 MA(k = 1)가 약 5%의 강한 스펙트럼 누출을 제공할 때, 실질적인 목적을 위해 3 ~ 5 범위 내의 k를 선택하는 것으로 충분하다.

최적성

KZ 필터는 견고하고 거의 최적입니다.KZ 필터는 단순한 이동 평균이기 때문에 데이터 누락 환경, 특히 데이터 누락이 공간적 희박성으로 인한 문제를 일으킬 수 있는 다차원 시공간에서 뛰어난 성능을 발휘합니다.KZ 필터의 또 다른 장점은 두 파라미터 각각이 명확한 해석을 가지고 있기 때문에 다른 분야의 전문가가 쉽게 채택할 수 있다는 것입니다.시계열, 종방향 및 공간 데이터를 위한 소프트웨어 구현은 다양한 영역에서 KZ 필터와 그 확장을 쉽게 사용할 수 있도록 인기 있는 통계 패키지 R로 개발되었다.

KZ 필터를 사용하여 Periodogram(주기율)을 매끄럽게 할 수 있습니다.확률적 프로세스의 클래스에 대해 주르벤코는^[1] 프로세스에 대해 사용할 수 있는 유일한 정보가 쾰더 조건에 의해 정량화된 스펙트럼 밀도와 부드러움인 최악의 시나리오를 고려했다.그는 스펙트럼 밀도의 기본 평활도에 따라 달라지는 스펙트럼 창의 최적 대역폭을 도출했다.주르벤코는^[1] 콜모고로프-주르벤코(KZ) 창의 성능을 바틀렛 창, 파르젠 창, 투키-해밍 창, 균일한 창 등 일반적으로 사용되는 다른 스펙트럼 창과 비교하고 KZ 창의 결과가 최적성에 가장 가깝다는 것을 보여주었다.

추상적인 이산 구조로 개발된 KZ 여과는 견고하고 통계적으로 거의 ^[1]최적입니다.동시에 자연 형태 때문에 계산상의 이점이 있어 관측치의 90%가 누락되고 여러 가지 다른 물리적 ^[2]현상의 복잡한 조합을 나타내는 데이터로 공간/시간 문제를 분석할 수 있다."해결 불가능한"^[2]^[3] 문제에 대한 명확한 답을 찾을 수 있습니다.일부 수학 발전과 달리 KZ는 ^[2]^[3]물리적인 해석이 명확하기 때문에 다른 분야의 전문가들에 의해 적응이 가능하다.

내선번호

그림 2:

θ m, k 0

= 0.

04,

m

=

100,

k

=

1

(검은색)

또는

k =

5

(빨간색)인 KZFT 필터의 전달 함수 로그.

그림 3: 단위 시간당 주파수 0.08 및 0.10 사이클에 대한 두 사인파의 합계에 70% 결측값을 갖는 노이즈 N(0,16)을 더한 신호의 스펙트럼.시뮬레이션 데이터 세트의 스펙트럼을 결정하기 위해 적응적으로 평활화된 KZP 알고리즘을 사용했다.

그림 4: 노이즈가 추가된 원래 신호에서 단위 시간당 0.08 및 0.10 사이클에 대한 두 사인파의 합이며 값의 60%를 사용할 수 없었던 재구성된 신호입니다.

KZ 필터의 확장에는 KZ 적응(^[1]KZA) 필터, 공간 KZ 필터 및 KZ 푸리에 변환(KZFT)이 포함됩니다.Yang과 Zurbenko는^[3] KZ 필터와 그 확장에 대한 자세한 리뷰를 제공했다.KZ 필터링을^[3]^[4]^[5] 구현하기 위한 R 패키지도 이용 가능

KZFT

KZFT 필터는 심한 노이즈로 덮인 주기적인 신호 또는 계절성을 재구성하기 위해 설계되었습니다.계절성은 시계열에서 자주 볼 수 있는 비정상성의 주요 형태 중 하나입니다.일반적으로 시계열 내의 주기적 성분으로 정의됩니다.스펙트럼 분석은 계절성을 가지고 시계열을 분석하는 강력한 도구입니다.프로세스가 정지해 있는 경우, 그 스펙트럼도 연속적인 형태입니다.예측의 단순성을 위해 모수적으로 처리할 수 있습니다.스펙트럼에 선이 포함되어 있는 경우는 프로세스가 정지하지 않고 주기성이 포함되어 있음을 나타냅니다.이 상황에서 모수 적합은 일반적으로 에너지가 감소된 계절 잔차를 초래합니다.이것은 계절에 따른 변화 때문이다.이 문제를 방지하려면 밴드 통과 필터를 포함한 비모수적 접근법을 사용하는 것이 좋습니다.^[3]Kolmogorov-Zurbenko Fourier Transform(KZFT; 콜모고로프-주르벤코 푸리에 변환)이 이러한 필터의 1개입니다.많은 애플리케이션의 목적은 노이즈가 많은 환경에서 고해상도 웨이브릿을 재구성하는 것입니다.KZFT가 스펙트럼 영역에서 최상의 분해능을 제공한다는 것이 입증되었다.이론적으로 가장 작은 거리의 가장자리에서 두 신호를 분리하거나, 과도한 노이즈로 뒤덮여 ^[3]^[6]불규칙적으로 관측되는 주기적인 신호를 재구성할 수 있습니다.이러한 이유로 KZFT는 다양한 응용 프로그램에 고유한 기회를 제공합니다.KZFT를 구현하기 위한 컴퓨터 알고리즘이 R 소프트웨어에서 제공되었습니다.KZFT는 본질적으로 고유한 시간 창을 가진 단시간 푸리에 변환(STFT) 범주에 속하는 밴드 패스 필터입니다.

KZFT는 컴퓨터 난수 발생기로부터 발생하는 백색 소음의 일정한 스펙트럼 밀도로부터 작은 편차를 쉽게 발견한다.이러한 컴퓨터 난수 생성은 장기적으로 예측 가능해진다.콜모고로프 복잡도는 예측할 수 없는 난수 ^[7]시퀀스를 생성할 수 있는 기회를 제공합니다.

공식적으로 $프로세스$ X $(), t$ $t$ = $...,$ 1, $0,1,...,$ 주파수 θ에서₀ 계산된 파라미터 m과 k를 가진 KZFT 필터는 출력 프로세스를 생성합니다. 출력 프로세스는 다음과 같이 정의됩니다.

(\displaystyle KZ)FT_{m,k,\nu _{0}}[X(t)]=\sum _{s=-k(m-1)/2}^{X(t+s)\times {a_{m,k}\times {e^{-i\nu_0}}}}{x(t+s)/2}}}}

어디 am,ks am,ks:).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{정의된다.Border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}Cm,ks/mk, s)−k(m− 1)/2,..., −k(m− 1)/2과 다항 계수 Cm,ks Σk(m− 1)r에 의해서 주어진다)0zrCk,mr− k(m− 1)/2)(1+z+...+z(m− 1))k. $분명히$ [ $X ($ t)]필터는 $프로세스 X(t + s - i 2(mν 0) s$ ) $e$ 에 (t $)$ 필터를 적용하는 것과 같다 $.$ 마찬가지로 KZFT 필터는 KZ 필터와 같은 방법으로 반복을 통해 얻을 수 있습니다.

S 기간에 걸친 시간 내 KZFT 제곱의 $평균인 0$ $δ$ $=$ 1/ $190$ 은₀ 모멘트 t 주위의 2Sµ₀ 관측에 기초한 주파수 δ₀ 또는 KZ 주기율(KZP)에서 파형의 제곱 진폭을 추정한다.

\operatorname {KZP} (t,m,k,\nu _{0})=2\left {frac {1}{2}S\rho _{0}}\sum _{\sum =-S\rho _{0}^{S\rho _{0}2\operatorname {Re} [KZFT_{m,k,\nu +0}[X(\tau +t)]^{2}\right

KZFT의 전송 함수는 그림 2에서 매우 날카로운 주파수 분해능을 $나타내며$ 대역폭은 c/( $mµk)$ 로 제한됩니다.복소수 $공정$ X $(t)$ = $e$ 의^i(2mν₀)t 경우 $KZFT m,k,ν 0 (t)$ 결과는 변경되지 않습니다.실제 가치 프로세스의 경우 에너지를 실제 및 복잡한 도메인에 균등하게 분배합니다.즉, $2Re[KZFT m,k,ν 0 (t)]$ 는 같은 주파수 θ의₀ 코사인 또는 사인파를 재구성한다.따라서 $2Re[KZFT m,k,ν 0 (t)]$ 는 주파수 θ를₀ 갖는 알 수 없는 파형의 진폭과 위상을 올바르게 재구성합니다.아래 그림은 KZFT 여과의 전력 전달 기능을 보여줍니다.이는 관심 주파수₀ θ = 0.4를 완벽하게 포착했으며 여과 파라미터 k로 제어하는 측면 로브에서 스펙트럼 누출이 거의 없음을 명확히 보여준다.실제적인 목적을 위해, 통상적인 FFT(k = 1)가 약 5%의 강한 누출을 제공할 때, 3-5 범위 내에서 k를 선택하는 것으로 충분합니다.

예: 시뮬레이션 신호
$결측값$ 이 있는 데이터 세트의 스펙트럼을 정확하게 결정하는 KZFT 알고리즘의 능력을 테스트하기 위해 sin $2π(0.10)t$ + $sin$ 2 $((0.02) t$ + normal random noise N(0,16)을 사용했다.실제적인 고려를 위해 스펙트럼이 지배적인 주파수를 계속 포착할 수 있는지 여부를 판단하기 위해 p=70%에서 결측값의 백분율을 사용했다.m=600과 k=3의 더 넓은 윈도우 길이를 사용하여 적응적으로 평활된 KZP 알고리즘을 사용하여 시뮬레이션된 세로 데이터 세트에 대한 스펙트럼을 결정했다.그림 3에서는 단위 시간당 0.08 및 0.10 사이클의 지배적인 주파수가 신호의 고유 주파수로 식별되는 것이 명백합니다.

종적 관측의 높은 노이즈에 포함된 원래 신호의 KZFT 재구성(누락률 60%)R-소프트웨어의 KZA 패키지의 KZFT 필터는 f = 주파수 매개변수를 갖는다.스펙트럼에서 발견된 각각의 알려진 지배적 주파수에 대해 이 파라미터를 정의함으로써 KZFT 필터는 파라미터 m=300 및 k=3으로 각 주파수에 대한 신호를 재구성합니다(단위 시간당 0.08 및 0.10 사이클).재구성된 신호는 KZFT 필터를 2회(각 지배 주파수 약 1회) 적용한 후 각 필터의 결과를 합산하여 결정되었습니다.참 신호와 재구성된 신호 사이의 상관 관계는 96.4%였습니다. 그림 4에 나와 있습니다.원래 관측치에서는 알고리즘에 의해 완벽하게 재구성된 복잡하고 숨겨진 주기성을 추측할 수 없습니다.

원시 데이터에는 숨겨진 주파수가 포함되어 있는 경우가 많습니다.소수의 고정 주파수파를 조합하면 신호의 혼합 인식을 복잡하게 만들 수 있지만 시간이 지남에 따라 예측 가능한 상태로 유지됩니다.출판물에^[3]^[6] 따르면 대기압은 달의 중력과 태양의 하루 주기에 기인하는 숨겨진 주기성을 포함하고 있다.이러한 대기 해일의 주기적인 신호를 재구성하면 극한의 날씨에 존재하는 많은 이상 징후를 설명하고 예측할 수 있다.행성의 중력에 의한 태양에도 비슷한 해일이 존재해야 한다.태양의 자전은 지구의 적도 전류와 비슷한 전류를 발생시킨다.해류 주변의 섭동이나 소용돌이는 태양 표면에 이상을 일으킬 것이다.고자성 플라즈마에서 수평 회전 에드는 수직 폭발을 일으켜 더 깊고 뜨거운 플라즈마를 태양 표면 위로 운반합니다.각각의 행성은 태양에 특정한 주파수의 해일을 만든다.때로는 두 개의 파동이 위상을 이루기도 하고, 다른 파동은 위상을 벗어나기도 합니다.결과 진폭이 다른 주파수로 진동합니다.DZ 알고리즘을^[3]^[6] 사용하여 흑점 데이터의 스펙트럼을 추정하면 주기성이 9.9년과 11.7년에 가까운 두 개의 선명한 주파수 라인을 얻을 수 있다.이러한 주파수 선은 목성과 토성(9.9)과 금성과 지구(11.7)에 의한 차이 주파수로 볼 수 있습니다.9.9와 11.7 사이의 차이 주파수는 64년의 주기를 갖는 주파수를 산출합니다.이 모든 기간은 태양 흑점 데이터에서 식별할 수 있습니다.64년 주기 구성요소는 현재 감소 ^[3]^[4]모드에 있습니다.이러한 감소는 가까운 미래에 지구에 냉각 효과를 일으킬 수 있다.여러 행성의 공동 효과를 조사하는 것은 태양 활동에서 오랜 기간을 발견할 수 있고 지구의 기후 변동을 설명하는 데 도움이 될 수 있습니다.

KZA

그림 5a: 신호 플롯 + 계절성 + 노이즈그림 5b: 그림 5a의 데이터에서 분리된 신호의 KZA 재구성.파란색 선은 원래 신호를 검은색 선으로 재구성한 것입니다.

그림 6: 그림 5a의 데이터에 대한

KZFT m, k

적용일반 로우패스 필터는 장기 컴포넌트의 파손을 재현할 수 없습니다.

KZ 적응형(KZA) 필터라고 불리는 KZ 필터의 적응형 버전은 심한 노이즈로 덮인 비모수 신호의 단절을 검색하기 위해 개발되었습니다.KZA 필터는, 최초로 브레이크가 발생했을 때의 잠재적인 시간 간격을 특정합니다.그런 다음 평활된 결과의 분해능이 증가하도록 창 크기를 줄여 이러한 시간 간격을 더 주의 깊게 조사합니다.

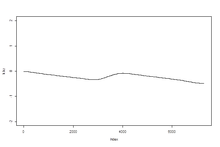
중단점 검출의 예로서 계절성과 노이즈에 매몰된 중단이 포함된 장기 추세를 시뮬레이션합니다.그림 2는 진폭이 1 단위인 계절 $사인파$ , 정규 분포 노이즈(노이즈 = $1$ ) 및 브레이크가 있는 기본 신호의 그래프입니다.더 어려운 것은 기본 신호에는 전체 하향 추세 1유닛과 상향 브레이크 0.5유닛이 포함되어 있다는 것입니다.원래 데이터에서는 하락 추세와 하락이 거의 보이지 않습니다.기본 신호는 스텝 $함수$ y = $-1 / 7300t$ $+ sin(2µt)$ 이며 $,$ $t$ < $3452$ 및 y $= -1 / 7300 (t$ - $3452)$ + sin( $2µt)$ 은 $3452$ $<$ t < $7300$ 입니다.원래 데이터에 저역 평활 $필터 3,365$ KZ를 적용하면 그림 6과 같이 파손이 지나치게 평활화된다.브레이크의 위치가 더 이상 명확하지 않습니다.KZ 필터(KZA)의 적응 버전을 적용하면 그림 5b와 같이 브레이크가 발견됩니다.KZA의 구성은 반복 평활 필터 KZ의 적응 버전을 기반으로 합니다.KZ에서 발견된 트렌드에 따라 필터링 창의 크기를 변경하는 것이 아이디어입니다.이렇게 하면 필터가 데이터가 변경되는 영역을 확대합니다. 변경이 빠를수록 줌이 더 촘촘해집니다.KZA를 구성하는 첫 번째 단계는 KZ $[X (t)]$ 를_q,k 사용하는 것입니다.여기서 k는 반복이고 q는 필터 길이입니다. $여기$ 서_q,k KZ는 반복 이동 $평균 i$ y= 1 $/(2q+ Σ q j=-q 1$ ) $X$ 이며_i+j, $여기$ 서_i x는 원본 데이터이고 $y$ 는_i 필터링된 데이터입니다.이 결과는 필터의 적응 버전을 구축하는 데 사용됩니다.필터는 각각 헤드와 테일(q와_b q)로_f 구성되며, 데이터에 따라 크기를 조정하는 f = 헤드와 b = 테일(f = head 및 b = tail).두부_f q는 데이터의 중단에 따라 축소됩니다.KZ; $D (t)$ = $Z (t$ $+ q$ ) - $Z (t$ $-$ q)에서 작성된 차분 벡터는 D'( $t)$ = $D (t +$ 1) - $D (t)$ 의 이산 등가물을 구하는 데 사용됩니다. 이 결과는 필터링 창의 헤드와 테일(q_f_b 및 q)의 크기를 각각 결정합니다.기울기가 양의 경우 헤드는 축소되고 꼬리는 전체 크기( $D$ '( $t)$ > $0$ ), f( $D (t) =$ 1 - $D (t)/ max[D (t)]$ 인q( $t)$ $및 b$ $q$ $(t)$ = q)로_f 확장됩니다 $.$ 기울기가 음수인 경우, 윈도우의 머리는 풀사이즈가 되고 꼬리는 축소됩니다( $D$ '( $t)$ < $0$ , 그 $후 f$ q( $t)$ = q $및 b$ q( $t)$ = $f (D (t) q$ ).KZA의 상세 코드를 이용할 수 있습니다.

그림 7: 정상 노이즈에 매몰된 레벨 1의 2차원 신호의 사각 이미지 θ=2의 재구성.왼쪽은 노이즈가 많은 이미지, 오른쪽은 2차원 KZA를 적용한 이미지입니다.총 표시 필드는 100 x 100 포인트이며, 원본 이미지는 중앙에 30 x 30 포인트입니다.

KZA 알고리즘은 비모수적 접근법의 모든 일반적인 장점을 가지고 있으며, 조사 중인 시계열의 특정 모델이 필요하지 않습니다.심한 노이즈로 덮인 모든 성질의 저주파 신호에서 갑작스러운 변화를 검색합니다.KZA는 신호 대 잡음비가 매우 낮더라도 브레이크 검출에 매우 높은 감도를 보이고 브레이크 시간 검출의 정확성도 매우 높습니다.

KZA 알고리즘을 적용하여 노이즈가 많은 2차원 영상을 복원할 수 있습니다.이것은, 강한 노이즈에 의한 흑백 화상으로서 2 레벨의 함수 f(x,y) 또는 멀티 레벨의 칼라 화상입니다.KZA를 라인별로 적용하여 파손(색상의 변화)을 검출할 수 있습니다.그러면 다른 라인의 파손점은 일반 KZ ^[3]필터에 의해 평활됩니다.공간 KZA의 시연은 그림 7에 나와 있습니다.

스펙트럼 내의 선명한 주파수 라인의 결정은 적응적으로 평활화된 주기문자에 ^[3]의해 결정될 수 있다.알고리즘의 중심 아이디어는 KZ 주기도의 대수를 적응적으로 평활화하는 것입니다.평활의 범위는 총 엔트로피에서 조건부 엔트로피의 일정한 비율로 제공됩니다.대략적으로 말하면, 알고리즘은 주파수 척도가 아닌 정보 척도로 균일하게 동작합니다.이 알고리즘은 KZP의 파라미터 k=1에 대해서도 Dirienzo-Zurbenko 알고리즘으로 알려져 있으며 소프트웨어에서 제공됩니다.

공간 KZ 필터

공간 KZ 필터는 시공간으로 기록된 변수에 적용할 수 있습니다.필터의 파라미터는 시간과 공간에서 개별적으로 선택할 수 있습니다.일반적으로 물리적 감각은 공간 내에서 어느 정도의 평균화 척도가 합리적인지, 시간적으로는 어느 정도의 평균화 척도가 타당한지를 적용할 수 있습니다.파라미터 k는 필터 분해능의 선명도 또는 주파수 리크 억제를 제어하고 있습니다.공간 KZ 필터 알고리즘은 R 소프트웨어에서 사용할 수 있습니다.결과시간 파라미터는 가상시간으로 처리하여 공간여과 결과의 영상을 가상시간에 "동영상"으로 표시할 수 있다.시간 t, 경도 x 및 위도 y의 함수로 온도 T(t, x, y)의 세계 기록에 적용된 3D 공간 KZ 필터를 시연할 수 있다.지구 기후 변동 성분 매개변수를 선택하기 위해 시간 t에 대해 25개월, KZ 필터링에 대해 경도와 위도에 대해 3°를 선택했습니다.척도 분해능을 수용하기 위해 매개변수 k는 5와 동일하게 선택되었다.아래 그림 8에 "동영상" 결과의 단일 슬라이드가 나와 있습니다.위도를 따라 낮은 표준 평균 코사인 제곱 온도 분포를^[4] 빼서 시간과 공간의 기후 변동을 식별했다.

그림 8: 2007년 12월 KZ 필터 m = (3°, 3°, 25개월), k = 5(위도 및 고도에 따라 조정됨).

2007년 코사인 제곱법칙에서 온도의 이상변동을 볼 수 있습니다.온도 이상은 우측 그림 눈금으로 지구 전체에 표시됩니다.지난 100년 동안 지속되었던 유럽과 북아프리카에 비해 매우 높은 양의 이상 징후를 보입니다.절대 습도 변수는 최근 콜모고로프-주르벤코 필터에서 주르벤코 이고르와 스미스 데빈이 시공간 ^[8]분석에서 보여준 것과 같이 주요 지역 기후 변화에 대한 책임이 있다.이러한 이상 징후는 KZ 여과 결과 "동영상"에서 시간에 따라 서서히 변화하고 있으며, 관찰된 이상 징후의 느린 강도는 시간에 따라 확인되었다.공간 KZ 여과로 El Nino 척도 등의 다른 스케일 변동도 확인할^[4] 수 있다.이러한 스케일의 고화질 "영화"는^[4] 북미 전역에서 제공됩니다.다른 변수에 대해 다른 척도를 KZ 필터링으로 선택할 수 있으며, 해당 다변량^[3]^[6] 분석은 다른 공변량보다 결과 변수를 조사하는 데 높은 효율성 결과를 제공할 수 있습니다.KZ 필터 분해능은 기존 방법에 비해 매우 우수하며 계산적으로 최적입니다.

실장

W. Yang 및 I. Zurbenko. kzft: Kolmogorov-Zurbenko 푸리에 변환 및 응용.R 패키지, 2006.
B. Close and I. Zurbenko. kza: 이미지 검출을 위한 Kolmogorov-Zurbenko 적응 알고리즘.R 패키지, 2016년 (https://cran.r-project.org/web/packages/kza/)
Andreas Weiler와 Michael Grossniklaus(독일 Konstanz 대학)의 1차원 어레이에 KZA 및 KZA Java 구현(https://web.archive.org/web/20140914054417/http)
Mathieu Schopfer(스위스 로잔 대학)의 KZ, KZFT 및 KZP의 Python 구현(https://github.com/MathieuSchopfer/kolmogorov-zurbenko-filter)

레퍼런스

^ ^a ^b ^c ^d ^e ^f ^g I. 주르벤코시계열의 스펙트럼 분석.North-Holland Series in Statistics and Probability, 1986.
^ ^a ^b ^c Zurbenko, I.; Porter, P. S.; Gui, R.; Rao, S. T.; Ku, J. Y.; Eskridge, R. E. (1996). "Detecting Discontinuities in Time Series of Upper-Air Data: Development and Demonstration of an Adaptive Filter Technique". Journal of Climate. 9 (12): 3548. Bibcode:1996JCli....9.3548Z. doi:10.1175/1520-0442(1996)009<3548:DDITSO>2.0.CO;2. ISSN 1520-0442.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l Yang, Wei; Zurbenko, Igor (2010). "Kolmogorov-Zurbenko filters". Wiley Interdisciplinary Reviews: Computational Statistics. 2 (3): 340–351. doi:10.1002/wics.71.
^ ^a ^b ^c ^d ^e Zurbenko, IG; Cyr, DD (2013). "Climate fluctuations in time and space: Addendum to Zurbenko & Cyr (2011)". Climate Research. 57 (1): 93–94. Bibcode:2013ClRes..57...93Z. doi:10.3354/cr01168.
^ B.Close, I. Zurbenko, Kolmogorov-Zurbenko 적응 알고리즘, Proceedings JSM, 2011
^ ^a ^b ^c ^d Zurbenko, Igor G.; Potrzeba, Amy L. (2013). "Tides in the atmosphere". Air Quality, Atmosphere & Health. 6: 39–46. doi:10.1007/s11869-011-0143-6. S2CID 94420644.
^ Zurbenko, I.G. (1993). "On weakly correlated random numbers generator". Journal of Statistical Computation and Simulation. 47 (1–2): 79–88. doi:10.1080/00949659308811512.
^ Zurbenko, Igor G.; Smith, Devin (2018). "Kolmogorov-Zurbenko filters in spatiotemporal analysis". Wiley Interdisciplinary Reviews: Computational Statistics. 10: e1419. doi:10.1002/wics.1419.

[z86-1] ^ ^a ^b ^c ^d ^e ^f ^g I. 주르벤코시계열의 스펙트럼 분석.North-Holland Series in Statistics and Probability, 1986.

[zprkge-2] Zurbenko, I.; Porter, P. S.; Gui, R.; Rao, S. T.; Ku, J. Y.; Eskridge, R. E. (1996). "Detecting Discontinuities in Time Series of Upper-Air Data: Development and Demonstration of an Adaptive Filter Technique". Journal of Climate. 9 (12): 3548. Bibcode:1996JCli....9.3548Z. doi:10.1175/1520-0442(1996)009<3548:DDITSO>2.0.CO;2. ISSN 1520-0442.

[yz10-3] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l Yang, Wei; Zurbenko, Igor (2010). "Kolmogorov-Zurbenko filters". Wiley Interdisciplinary Reviews: Computational Statistics. 2 (3): 340–351. doi:10.1002/wics.71.

[zc-4] Zurbenko, IG; Cyr, DD (2013). "Climate fluctuations in time and space: Addendum to Zurbenko & Cyr (2011)". Climate Research. 57 (1): 93–94. Bibcode:2013ClRes..57...93Z. doi:10.3354/cr01168.

[cz-5] B.Close, I. Zurbenko, Kolmogorov-Zurbenko 적응 알고리즘, Proceedings JSM, 2011

[zp-6] Zurbenko, Igor G.; Potrzeba, Amy L. (2013). "Tides in the atmosphere". Air Quality, Atmosphere & Health. 6: 39–46. doi:10.1007/s11869-011-0143-6. S2CID 94420644.

[7] Zurbenko, I.G. (1993). "On weakly correlated random numbers generator". Journal of Statistical Computation and Simulation. 47 (1–2): 79–88. doi:10.1080/00949659308811512.

[8] Zurbenko, Igor G.; Smith, Devin (2018). "Kolmogorov-Zurbenko filters in spatiotemporal analysis". Wiley Interdisciplinary Reviews: Computational Statistics. 10: e1419. doi:10.1002/wics.1419.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Search

콜모고로프-주르벤코 필터

네임스페이스

더

목차

배경

정의.

특성.

최적성

내선번호

실장

레퍼런스