관계(수학)

수학에서 집합의 관계는 집합의 주어진 두 멤버 사이에 성립할 수도 있고 그렇지 않을 수도 있습니다. 예를 들어, "미만"은 자연수 집합에 대한 관계이며, 예를 들어 1과 3 사이(1 < 3으로 표시됨) 및 3과 4 사이(3 < 4로 표시됨)는 동일하지만 3과 1 사이 또는 4와 4 사이(3 < 4로 표시됨)는 그렇지 않습니다. 즉, 3 < 1은 거짓으로 평가되며, 4 < 4도 마찬가지입니다. 또 다른 예로, "is sis sister of"는 모든 사람들의 집합에 대한 관계로, 예를 들어 마리 퀴리와 브로니스와와 드뷔스카 사이에 존재하며, 마찬가지로 그 반대의 경우도 있습니다. 설정된 구성원은 "어느 정도" 관계에 있지 않을 수 있습니다. 관계에 있거나 관계에 있지 않을 수 있습니다.

공식적으로 집합 X에 대한 관계 R은 X의 구성원들의 순서쌍 (x,y)의 집합으로 볼 수 있습니다.^[1] (x,y)가 R의 구성원이면 관계 R은 x와 y 사이에 성립합니다. 예를 들어, 자연수에서 "미만"이라는 관계는 (1,3)과 (3,4)를 모두 포함하지만 (3,1)과 (4,4)는 포함하지 않는 자연수 쌍의 무한 집합 R입니다_less. 한 자리 자연수의 집합에서 "의 비유분수"라는 관계는 여기에 표시하기에 충분히 작습니다: R = { (2,4), (2,6), (2,8), (3,6), (3,9), (4,8) }; 예를 들어 2는 8의 비유분수이지만 그 반대는 아니므로 (2,8) ∈ R이지만 (8,2) ∉ R입니다.

만약 R이 x와 y를 유지하는 관계라면, 종종 xRy를 씁니다. 수학에서 가장 일반적인 관계에서는 "이하"를 나타내는 "<", "의 비사분수를 나타내는 "="와 같이 특수 기호가 도입됩니다. 예를 들어, "1 < 3", "1은 3보다 작음", "(1,3) ∈ R"은 모두 동일한 의미이며, 일부 저자는 "(1,3) ∈(<)"를 쓰기도 합니다.

관계의 다양한 속성이 조사됩니다. xRx가 모든 x에 대하여 성립하면 관계 R은 반사적이고, xRx가 n에 대하여 성립하면 반사적이지 않습니다. xRy가 항상 yRx를 의미하면 대칭이고, xRy가 yRx가 불가능함을 의미하면 비대칭입니다. xRy 및 yRz가 항상 xRz를 의미하는 경우 이는 추이적입니다. 예를 들어, "보다 작음"은 반사적이지 않고 비대칭적이며 과도적이지만 반사적이지도 않고 대칭적이지도 않습니다. "sis sister of"는 추이적이지만 반사적이지도 않고(예: 피에르 퀴리는 자신의 여동생이 아닙니다) 대칭적이지도 않고 비대칭적이지도 않습니다. (모든 여성이 자신의 여동생인가요?) 반사적이지도 않고 정의의 문제일 수 있지만, "의 조상은 추이적인 반면"의 부모는 그렇지 않습니다. 수학적 정리는 "가변 관계가 비대칭인 경우에만 무반전적이다"와 같은 관계 속성의 조합에 대해 알려져 있습니다.

특히 중요한 것은 속성의 특정 조합을 만족시키는 관계입니다. 부분 순서는 반사적이고 반대칭적이며 과도적인 관계이고,^[2] 등가 관계는 반사적이고 대칭적이며 과도적인 관계이고,^[3] 함수는 우-고유적이고 전체적인 관계입니다(아래 참조).^[4][5]

관계는 집합이므로 집합 연산을 사용하여 조합, 교집합, 상보 등을 포함하고 집합 대수의 법칙을 만족하여 조작할 수 있습니다. 그 외에도 관계의 역방향과 관계의 구성과 같은 연산이 가능하여 관계 미적분학의 법칙을 만족합니다.^[6][7][8]

위의 관계^[a] 개념은 서로 다른 두 집합의 구성원 사이의 관계(예를 들어, 기하학에서 모든 점의 집합과 모든 선의 집합 사이의 "누워져 있는" 것과 같은 이질적인 관계), 세 개 이상의 집합 사이의 관계(예를 들어, "개인 x가 시간 z에서 마을 y에 살고 있는" 것과 같은 유한 관계), 클래스 간의 관계(모든 집합의 클래스에 대한 "의 요소"와 같이 이진 관계 § 집합 대 클래스 참조).

정의.

집합 X가 주어졌을 때, X에 대한 관계 R은 형식적으로 R ⊆ { (x,y) x, y ∈ X}인 원소들의 순서 쌍들의 집합입니다.

(x,y) ∈ R은 "x는 y와 관련된 R"이라고 읽으며, xRy로 infix 표기법으로 쓰여집니다. 요소의 순서는 중요합니다. 만약 x ≠y이면 yRx는 xRy와 무관하게 참이거나 거짓일 수 있습니다. 예를 들어, 3은 9를 나누지만 9는 3을 나누지 않습니다.

관계의 대표성

y x	1	2	3	4	6	12
1
2
3
4
6
12
R의div 표현 부울 행렬로서

유한 집합 X 위의 관계 R은 다음과 같이 나타낼 수 있습니다.

• 방향 그래프: X의 각 구성원은 정점에 해당하며, (x,y) ∈ R인 경우에만 x에서 y로의 방향 간선이 존재합니다.
• 부울 행렬: X의 구성원들은 어떤 고정된 순서 x, ..., x로 배열됩니다; 행렬은 n × n의 차원을 가지며, 원소는 i, 열 j이고, 는 (x,x) ∈ R이고, 그렇지 않으면 , 입니다.
• 2D-플롯: 부울 행렬의 일반화로서 실수의 –무한 집합 R 위의 관계는 2차원 기하 도형으로 표현될 수 있습니다: 직각좌표를 사용하여 (x,y) ∈ R일 때마다 (x,y)에 점을 그립니다.

유한 집합 X 위의 추이^[c] 관계 R은 다음과 같이 표현될 수도 있습니다.

• 해시 다이어그램: X의 각 구성원은 정점에 해당합니다. 방향 에지는 (x,y) ∈ R인 경우에만 x에서 y로의 방향 경로가 존재하도록 그려집니다. 방향 그래프 표현에 비해 하세 다이어그램은 덜 엉킨 이미지로 이어집니다. "x에서 y까지 방향 경로가 존재한다"는 관계는 추이적이므로, 추이적 관계만 Hasse 다이어그램으로 나타낼 수 있습니다. 일반적으로 다이어그램은 모든 모서리가 위쪽 방향을 가리키도록 배치되며 화살표는 생략됩니다.

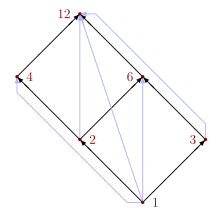
예를 들어, 모든 나눗셈들의 집합 12 위에서, 관계 R을_div 다음과 같이 정의합니다.

x R_div y if x is a divisor of y and x ≠ y.

Formally, X = { 1, 2, 3, 4, 6, 12 } and R_div = { (1,2), (1,3), (1,4), (1,6), (1,12), (2,4), (2,6), (2,12), (3,6), (3,12), (4,12), (6,12) }. R을_div 부울 행렬로 표현하면 중간 표에 표시되며, Hasse 다이어그램과 방향 그래프로 표현하면 왼쪽 그림에 표시됩니다.

다음은 동등합니다.

• x Ry는_div 사실입니다.
• (x,y) ∈ R
• R을_div 나타내는 하세 다이어그램에는 x에서 y로의 경로가 있습니다.
• R을_div 나타내는 방향 그래프에는 x부터 y까지의 간선이 존재합니다.
• R을_div 나타내는 부울 행렬에서 x행, y열의 원소는 ""입니다.

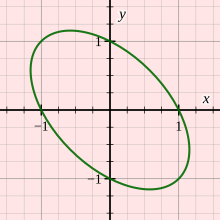
다른 예로 R에 대한 관계 R을_el 다음과 같이 정의합니다.

x R_el y if x² + xy + y² = 1.

R을_el 2D 그림으로 표현하면 타원을 얻을 수 있습니다. 오른쪽 그림을 참조하십시오. R은 유한하지도 않고, 방향 그래프도 아니고, 유한 부울 행렬도 아니므로, 하세 다이어그램을 사용하여 R을_el 묘사할 수 없습니다.

관계의 속성

집합 X에 대한 관계 R이 가질 수 있는 몇 가지 중요한 성질은 다음과 같습니다.

반사적

for all x ∈ X, xRx. 예를 들어, ≥는 반사 관계이지만 >는 반사 관계가 아닙니다.

무반전(또는 엄격)

for all x ∈ X, not xRx. 예를 들어 >는 비굴절 관계인데 ≥는 그렇지 않습니다.

앞의 두 대안은 완전하지 않습니다. 예를 들어 아래 다이어그램에 주어진 빨간색 관계 y = x는 각각 쌍 (0,0)을 포함하지만 (2,2)는 포함하지 않기 때문에 무반사적이거나 반사적이지 않습니다.

대칭

for all x, y ∈ X, if xRy then yRx. 예를 들어, y가 x의 혈족일 경우에만 x가 y의 혈족이기 때문에 "의 혈족"은 대칭 관계입니다.

반대칭

for all x, y ∈ X, if xRy and yRx then x = y. 예를 들어, ≥는 반대칭 관계이며 >도 마찬가지이지만 공백(정의의 조건은 항상 거짓)입니다.

비대칭적

for all x, y ∈ X, if xRy then not yRx. 관계가 반대 대칭이고 무반전인 경우에만 비대칭입니다.^[11] 예를 들어 >는 비대칭 관계인데 ≥는 그렇지 않습니다.

다시 말하지만, 앞의 세 가지 대안은 완전하지 않습니다. 자연수보다 예를 들어 x > 2로 정의된 관계 xRy는 비대칭은 고사하고 대칭(예: 5R1, 1R5는 아님)도 반대칭(예: 6R4, 4R6)도 아닙니다.

트랜지티브

for all x, y, z ∈ X, if xRy and yRz then xRz. 전이 관계는 비대칭인 경우에만 굴절되지 않습니다.^[12] 예를 들어, "의 조상"은 천이 관계인 반면, "의 부모"는 천이 관계가 아닙니다.

연결된

for all x, y ∈ X, if x ≠ y then xRy or yRx. 예를 들어, 자연수에서 <는 연결되어 있는 반면, "의 약수"는 연결되어 있지 않습니다(예: 5R7이나 7R5 모두 연결되어 있지 않습니다).

강력하게 연결됨

for all x, y ∈ X, xRy or yRx. 예를 들어, 자연수에서는 ≤가 강하게 연결되어 있지만 <는 연결되어 있지 않습니다. 관계는 그것이 연결되어 있고 반사적인 경우에만 강하게 연결됩니다.

고유 속성:

주사^[d](왼쪽 고유라고도^[13] 함)

For all x, y, z ∈ X, if xRy and zRy then x = z. 예를 들어 다이어그램의 녹색 및 파란색 관계는 주입식이지만 빨간색 관계는 (-1 및 1 대 1 모두와 관련됨에 따라) 검은색 관계가 아닙니다. (-1 및 1 대 0 모두와 관련됨에 따라) 검은색 관계도 아닙니다.

함수^[d](오른쪽 고유,^[13] 오른쪽^[14] 정의 또는 무가치라고도^[8] 함)

For all x, y, z ∈ X, if xRy and xRz then y = z. 그러한 관계를 부분 함수라고 합니다. 예를 들어, 다이어그램의 빨간색과 녹색 관계는 기능적이지만 파란색 관계는 (1이 -1과 1 모두에 관련됨에 따라) 검은색 관계도 아닙니다(0이 -1과 1 모두에 관련됨에 따라).

토탈리티 속성:

직렬^[d](전체 또는 왼쪽-전체라고도 함)

모든 x ∈ X에 대하여, xRy와 같은 y ∈ X가 존재합니다. 이와 같은 관계를 다중값 함수라고 합니다. 예를 들어, 다이어그램의 빨간색과 녹색 관계는 전체적이지만 파란색 관계는 (-1은 어떤 실수와도 관련이 없기 때문에) 검은색 관계도 아닙니다. (2는 어떤 실수와도 관련이 없기 때문에) 또 다른 예로 >는 정수에 대한 직렬 관계입니다. 그러나 양의 정수에는 1 > y 정도의 양의 정수가 없기 때문에 양의 정수에 대한 직렬 관계가 아닙니다.^[15] 그러나 <는 양의 정수, 유리수 및 실수에 대한 직렬 관계입니다. 모든 반사 관계는 직렬입니다. 주어진 x에 대해 y = x를 선택합니다.

서젝티브^[d](오른쪽-전체^[13] 또는 위쪽이라고도 함)

모든 ∈ Y에 대하여 xRy와 같은 x ∈ X가 존재합니다. 예를 들어 다이어그램의 녹색 및 파란색 관계는 주관적이지만 빨간색 관계는 (실수를 -1과 관련시키지 않으므로) 검은색 관계가 아닙니다 (실수를 2와 관련시키지 않으므로).

속성의 조합

재산별관계

	반사성	대칭성	감수성	커넥티드니스	예
부분순서	리플	안티심	네.		부분 집합
엄격부분순서	언레플	심	네.		엄격 부분 집합
총주문량	리플	안티심	네.	네.	알파벳 순서
엄밀전순차	언레플	심	네.	네.	엄밀한 가나다순
등가관계	리플	심	네.		평등

위 속성의 특정 조합을 만족시키는 관계는 특히 유용하므로 이름을 자체적으로 받았습니다.

등가관계

반사적이고 대칭적이며 추이적인 관계. 이러한 특성은 반사성을 의미하기 때문에 대칭, 과도 및 직렬 관계이기도 합니다.

주문:

부분순서

반사적이고 반대칭적이며 추이적인 관계.

엄격부분순서

무반전적이고 비대칭적이며 추이적인 관계입니다.

총주문량

반사적이고, 반대칭적이고, 추이적이고, 연결된 관계.^[16]

엄밀전순차

무반전적이고 비대칭적이며 추이적이며 연결된 관계입니다.

고유 속성:

일대일^[d]

주사 및 기능적입니다. 예를 들어, 다이어그램의 녹색 관계는 일대일이지만 빨간색, 파란색 및 검은색 관계는 그렇지 않습니다.

일대다^[d]

주입식이며 작동하지 않습니다. 예를 들어, 다이어그램의 파란색 관계는 일대일이지만 빨간색, 녹색 및 검은색 관계는 그렇지 않습니다.

다대일^[d]

기능적이며 주사제가 아닙니다. 예를 들어, 다이어그램의 빨간색 관계는 다대일이지만 녹색, 파란색 및 검은색 관계는 그렇지 않습니다.

다대다^[d]

주사제도 기능도 없습니다. 예를 들어, 다이어그램의 검은색 관계는 다대 다이지만 빨간색, 녹색 및 파란색 관계는 그렇지 않습니다.

고유성 및 전체성 속성:

함수^[d].

함수적이고 전체적인 관계. 예를 들어, 다이어그램의 빨간색과 녹색 관계는 함수이지만 파란색과 검은색 관계는 함수가 아닙니다.

주사^[d].

주입식 기능입니다. 예를 들어 그림의 녹색 관계는 주입이지만 빨간색, 파란색 및 검은색은 주입이 아닙니다.

투찰^[d].

객관적인 함수입니다. 예를 들어, 다이어그램의 녹색 관계는 돌출 관계이지만 빨간색, 파란색 및 검은색은 돌출 관계가 아닙니다.

바이젝션^[d]

주입식 및 타의적인 함수입니다. 예를 들어, 다이어그램의 녹색 관계는 바이젝션이지만 빨간색, 파란색 및 검은색 관계는 바이젝션이 아닙니다.

관계에 대한 연산

연합^[e]

만약 R과 S가 X에 대한 관계라면 R ∪ S = { (x, y) xRy 또는 xSy}는 R과 S의 결합 관계입니다. 이 작업의 ID 요소는 빈 관계입니다. 예를 들어, ≤는 <와 =의 결합이고, ≥는 >와 =의 결합입니다.

교차점^[e]

R과 S가 X에 대한 관계라면 R ∩ S = { (x, y) xRy 및 xSy}는 R과 S의 교집합 관계입니다. 이 연산의 아이덴티티 요소는 보편적 관계입니다. 예를 들어, "is is a lower card of the suit"은 "is lower card is than"과 "suit of the suit"의 교차점입니다.

구성.^[e]

R과 S가 X에 대한 관계라면 S ∘ R = { (x, z)가 존재하므로 xRy와 ySz}(R; S로도 표시)는 R과 S의 조성 관계입니다. 아이덴티티 요소는 아이덴티티 관계입니다. 여기서 사용되는 표기 S ∘ R의 R과 S의 순서는 함수의 구성에 대한 표준 표기 순서와 일치합니다. 예를 들어, ∘의 어미는 수확량의 어미이고, ∘의 어미는 수확량의 어미이고, 반면에, ∘의 어미는 수확량의 어미입니다. 전자의 경우, 만약 x가 y의 부모이고 y가 z의 어머니라면, x는 z의 외조부모입니다.

컨버스^[e]

만약 R이 집합 X와 Y에 대한 관계라면 R = { (y, x) xRy}는 Y와 X에 대한 R의 반대 관계입니다. 예를 들어, =는 ≠와 마찬가지로 자신의 역이고, <와 >는 ≤와 ≥와 마찬가지로 서로의 역입니다.

보형물^[e]

R이 X에 대한 관계라면 R = { (x, y) x, xRy}가 아닌 y ∈ X(R 또는 ¬R로도 표시)는 R의 상보 관계입니다. 예를 들어, =와 ≠는 서로 보완적이며, ⊆와 ⊈, ⊇와 ⊉, ∈와 ∉도 마찬가지이며, 총 주문의 경우 <와 ≥, >와 ≤도 마찬가지입니다. 역 관계 R의 여집합은 $여집합$의 역이다: R ${\displaystyle T^{}\stackrel{}{{}^{}}}$¯ =$R$¯ T.${\displaystyle${\$overline${R^{\mathsf {T}}}={\bar {R}}^{\mathsf {T}}.

제한^[e]

R이 X에 대한 관계이고 S가 X의 부분 집합이면 R = { (x, y) xRy 및 x, y ∈ S}는 R에서 S까지의 제한 관계입니다. 식 R = { (x, y) xRy 및 x ∈ S}는 R 대 S의 왼쪽 restrict 관계이고, R = { (x, y) xRy 및 y ∈ S}는 R 대 S의 오른쪽 restrict 관계라고 합니다. 관계가 반사적, 비반사적, 대칭적, 반대칭적, 비대칭적, 과도적, 총, 삼차성, 부분 순서, 총 순서, 총 순서, 엄격한 약한 순서, 총 전 순서(약한 순서) 또는 등가 관계인 경우, 그 제한도 마찬가지입니다. 그러나 제한의 일시적 폐쇄는 일시적 폐쇄의 제한의 하위 집합으로, 일반적으로 동일하지 않습니다. 예를 들어, "x는 y의 부모이다"라는 관계를 여성에게 제한하면 "x는 여성의 어머니이다"라는 관계가 생성됩니다. 그것의 일시적인 폐쇄는 여성과 친할머니를 연관시키지 않습니다. 반면에, "is parent of"의 일시적인 폐쇄는 "is store of"이며, 여성에 대한 제한은 여성과 친할머니를 연관시킵니다.

관계 R이 X와 Y 위의 관계 S, R이 S의 부분 집합이면 R ⊆ S, 즉 모든 x ∈ X와 y ∈ Y에 대해 xRy이면 xSy에 포함된다고 합니다. 만약 R이 S에 포함되고 S가 R에 포함된다면, R과 S는 동등하게 쓰여진 R = S라고 불립니다. 만약 R이 S에 포함되지만 S가 R에 포함되지 않는다면, R은 S보다 작다고 말하고, R ⊊ S입니다. 예를 들어, 유리수 위에서 관계 >는 ≥보다 작고, 구성 > ∘ >와 같습니다.

관계에 대한 정리

• 관계가 반대 대칭이고 비반전적인 경우에만 비대칭입니다.
• 전이 관계는 비대칭인 경우에만 굴절되지 않습니다.
• 관계는 그 보체가 반사적이지 않을 경우에만 반사적입니다.
• 관계는 그것이 연결되어 있고 반사적인 경우에만 강하게 연결됩니다.
• 관계는 대칭인 경우에만 역수와 같습니다.
• 관계는 그 여집합이 반대칭인 경우에만 연결됩니다.
• 관계는 그 보체가 비대칭인 경우에만 강하게 연결됩니다.^[17]
• 관계 R이 관계 S에 포함되어 있다면,
  • R이 반사적이고, 연결되어 있고, 강하게 연결되어 있고, 왼쪽 전체이거나, 오른쪽 전체이거나, S도 마찬가지입니다.
  • S가 무반곡, 비대칭, 반대칭, 좌-유일 또는 우-유일이면 R도 마찬가지입니다.
• 관계는 각각 반사적, 비반사적, 대칭적, 비대칭적, 반대칭적, 연결된, 강하게 연결된, 과도적입니다.

예

• 엄격한 주문을 포함한 주문 관계:
  • 보다 큼
  • 크거나 같음
  • 보다 적은
  • 이하
  • 나눗셈(짝수)
  • 의 부분 집합
• 동등성 관계:
  • 평등
  • (아핀 공간의 경우)와 평행
  • 주사를 맞고 있습니다.
  • 동형
• 공차 관계, 반사 및 대칭 관계:
  • 종속 관계, 유한 공차 관계
  • 독립 관계, 일부 종속 관계의 보완
• 친족관계

일반화

위의 관계 개념은 서로 다른 두 집합의 구성원 간의 관계를 인정하는 것으로 일반화되었습니다. 집합 X와 Y가 주어졌을 때, X와 Y에 대한 이질적인 관계 R은 { (x,y) x ∈X, y ∈Y}의 부분 집합입니다. X = Y일 때 위에서 설명한 관계 개념이 얻어지는데, 이를 일반화와 구별하기 위해 동차 관계(또는 내환 관계)라고 합니다. 각각 ^[d]"와 ^[e]"로 표시된 위의 속성과 연산은 이질적인 관계로 일반화됩니다. 이질적인 관계의 예로는 "해양과 대륙의 경계"가 있습니다. 가장 잘 알려진 예는 sqrt : N → R과 같이 서로 다른 도메인과 범위를 갖는 함수입니다.

참고 항목

• 점과 선의 집합 사이의 이질적인 관계인 발생 구조
• 순서 이론, 순서 관계의 속성을 조사합니다.

메모들

참고문헌

서지학