n차원 순차 이동 퍼즐

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "N차원 순차 이동 퍼즐" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2016년 1월) (이 템플릿 메시지 제거 방법과 시기 학습)

루빅스 큐브는 3차원 순차 움직임 퍼즐의 원형이자 가장 잘 알려져 있다.소프트웨어에서 이 퍼즐을 가상으로 구현한 것이 많았다.3차원이 넘는 순차 이동 퍼즐을 만드는 것은 자연스러운 연장이다.비록 그러한 퍼즐이 물리적으로 구성될 수는 없지만, 어떻게 작동하는지 규칙은 수학적으로 상당히 엄격하게 정의되어 있고 3차원 기하학에서 발견되는 규칙과 유사하다.따라서 소프트웨어로 시뮬레이션할 수 있다.기계적 순차 이동 퍼즐과 마찬가지로, 아직 같은 수준의 경쟁 조직은 아니지만 해결사에 대한 기록이 있다.

용어집

• 정점. 고차원 형상이 만나는 0차원 지점이다.
• 엣지. 고차원 형상이 만나는 1차원 형상이다.
• 면. (3보다 큰 차원의 물체의 경우) 고차원 형상이 만나는 2차원 형상이다.
• 세포. (4차원 이상의 물체의 경우) 고차원 형상이 만나는 3차원 형상이다.
• N-폴리토프위와 같이 계속되는 n차원 형상.특정한 기하학적 모양은 테서락트를 의미하는 4큐브와 같이 이것이 적절한 폴리토프를 대체할 수 있다.
• n세포. n세포가 들어 있는 고차원적 형상이다.
• 조각. 퍼즐의 한 이동 가능한 부분은 전체 퍼즐과 동일한 차원성을 가진다.
• 큐비. 해결 공동체에서 이것은 일반적으로 '피스'에 사용되는 용어다.
• 스티커.퍼즐의 상태를 식별하는 퍼즐의 색상 라벨.예를 들어, 루빅 큐브의 코너 큐빅은 한 조각이지만 각각 세 개의 스티커가 붙어 있다.고차원 퍼즐의 스티커는 2개 이상의 치수성을 가질 것이다.예를 들어, 4-큐브에서 스티커는 3차원 고형분이다.

비교를 위해 표준 3³ 루빅 큐브와 관련된 데이터는 다음과 같다.

피스 카운트
정점 수(V)	8	3색 조각 수	8
가장자리 수(E)	12	2색 조각 수	12
면 수(F)	6	1색 조각 수	6
셀 수(C)	1	0색 조각 수	1
색칠된 조각 수(P)	26
스티커 수	54

달성 가능한 조합의 수 = ${\displaystyle \frac{12!}{}}$ ${\displaystyle \frac{\cdot }{}}$ ${\displaystyle \frac{8!}{}}$ ${\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \cdot }$ ${\displaystyle 2\frac{{\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{\mathrm{}}}$ ${\displaystyle \cdot }$ ${\displaystyle 3\frac{{\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{\mathrm{}}}$~ ${\displaystyle {10}^{}}$ ${\displaystyle {20}^{}}$ ${\frac$ {$12!\cdot 8!$$}}{{2}}\cdot{12}}{2^{12}}}}{{3^{8}}}}\심각 10^{20}}}}}}$

얼굴 중심의 큐빅은 서로 상대적으로 움직일 수 없는 만큼 따로따로 계산해야 하는지에 대한 논란이 있다.다른 출처에 다른 수의 작품이 제공될 수 있다.이 글에서는 얼굴 중심 큐빅을 계산하는데, 이는 산술적 시퀀스를 보다 일관적으로 만들고 확실히 회전시킬 수 있기 때문에, 이 해결책은 알고리즘을 필요로 한다.다만 가운데 있는 큐비에는 눈에 보이는 스티커가 없어 해결책이 필요 없기 때문에 계산되지 않는다.산술적으로 우리는 해야 한다.

$P=V+E+F+C\,\!}$

그러나 C(또는 더 높은 차원에 대한 해당 최고차원 폴리토프)는 계산되지 않기 때문에 이 글에서 제시된 수치에서 P는 항상 이것(또는 이 공식의 n차원 확장)에 한 가지 모자란다.

매직 4D 큐브

기하학적 형상: 큐세락트

Superliminal MagicCube4D 소프트웨어는⁴ N 큐브를 포함한 4D 폴리토페의 많은 트위스트 퍼즐 버전을 구현한다.UI는 4D 트위스트 및 회전과 3D 투영, 큐비 사이즈 및 간격, 스티커 크기 등 4D 뷰잉 파라미터를 제어할 수 있다.

슈퍼리미날소프트웨어는 이 퍼즐을 깨뜨린 해결사들로 기록적인 명예의 전당을 유지하고 있다.

3⁴ 4시 30분

피스 카운트[1]
정점 수	16	4색조 수	16
가장자리 수	32	3색 조각 수	32
면 수	24	2색 조각 수	24
세포수	8	1색 조각 수	8
4-Cube 수	1	0색 조각 수	1
색칠된 조각 수	80
스티커 수	216

달성 가능한 조합:^[2]

${\displaystyle ={\frac {24!\cdot 32!}}{2}}\cdot{\frac{16!}}{2}}\cdot 2^{23}\cdot(3!)^{31}\cdot 3\cdot {\좌측값\frac {4!}}{2}}\오른쪽)^{15}\cdot 4}$

$\displaystyle \sim 10^{120}\,\!}$

2⁴ 4시 30분

피스 카운트[1]
정점 수	16	4색조 수	16
가장자리 수	32	3색 조각 수	0
면 수	24	2색 조각 수	0
세포수	8	1색 조각 수	0
4-Cube 수	1	0색 조각 수	0
색칠된 조각 수	16
스티커 수	64

달성 가능한 조합:^[2]

${\displaystyle {}={\frac {15!}}{2}}\cdot {\좌우 이동\frac {4!}}{2}}\오른쪽)^{14}\cdot 4}$

${\displaystyle {}\심 10^{28}\,\!}$

4시⁴ 15분

피스 카운트[1]
정점 수	16	4색조 수	16
가장자리 수	32	3색 조각 수	64
면 수	24	2색 조각 수	96
세포수	8	1색 조각 수	64
4-Cube 수	1	0색 조각 수	16
색칠된 조각 수	240
스티커 수	512

달성 가능한 조합:^[2]

${\displaystyle ={\frac {15!}}{2}}\cdot \lefts\frac {4!}}{2}}\오른쪽)^{14}\cdot 4\cdot {\frac {64!}}{{2}}\cdot 3^{63}\cdot {96!\cdot 2}{2\cdot (4!)^{24}}}\cdot {2^{95}\cdot 64!\cdot 2}{2\cdot (8!)^{8}}}}$

${\displaystyle \sim 10^{334}\,\!}$

5⁴ 4시 15분

피스 카운트[1]
정점 수	16	4색조 수	16
가장자리 수	32	3색 조각 수	96
면 수	24	2색 조각 수	216
세포수	8	1색 조각 수	216
4-Cube 수	1	0색 조각 수	81
색칠된 조각 수	544
스티커 수	1000

달성 가능한 조합:^[2]

${\displaystyle ={\frac {48!}{(6!)^{8}}\cdot {\frac {96!}{{8}}}\cdot {\frac {64!}{(8!)^{8}}\cdot {\frac {24!\cdot 32!}}{2}}\cdot(3!)^{31}\cdot 2^{23}\cdot {\frac {64!}}{2}}\cdot }$${\displaystyle 3^{63}\cdot 16!\cdot \leftfrac {4!}}{2}}\오른쪽)^{15}\cdot 4\cdot{96!}{\frac{96!}{24}}}\cdot 2^{95}\cdot{96!}{4!}}{24}}\cdot 2^{95}}}}$

${\displaystyle \sim 10^{701}\,\!}$

매직 5D 큐브

기하학적 형상: 펜터액트

그라비티3d 매직 5D 큐브 소프트웨어는 2부터⁵ 7까지⁵ 6가지 크기로 5큐브 퍼즐을 렌더링할 수 있다.큐브에서 이동하는 기능뿐만 아니라 보기를 변경하는 컨트롤도 있다.여기에는 Superliminal의 4D 큐브와 유사한 3-공간, 4-공간 및 5-공간, 4-D 및 5-D 투시 컨트롤, 큐비 및 스티커 간격 및 크기 컨트롤에서 큐브를 회전하는 컨트롤이 포함된다.

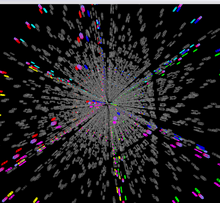
그러나 5-D 퍼즐은 4-D 퍼즐보다 2-D 화면에서 이해하는 것이 훨씬 어렵다.중력3d 구현의 필수적 특징은 선택한 큐빅과 스티커를 끄거나 강조표시하는 기능이다.그렇다 하더라도, 스크린샷에서 볼 수 있듯이, 생성된 이미지의 복잡성은 여전히 상당히 심각하다.

중력3d는 이 퍼즐의 해답을 깨는 기록들을 위해 정신병의 전당을 유지하고 있다.2011년 1월 6일 현재, 5-큐브 7⁵ 사이즈에 대한 두 가지 성공적인 해결책이 있다.^[3]

3⁵ 5시 30분

피스 카운트[1]
정점 수	32	5색 조각 수	32
가장자리 수	80	4색조 수	80
면 수	80	3색 조각 수	80
세포수	40	2색 조각 수	40
4-Cube 수	10	1색 조각 수	10
5-Cube 수	1	0색 조각 수	1
색칠된 조각 수	242
스티커 수	810

달성 가능한 조합:^[4]

${\displaystyle ={\frac {32!}}{2}}\cdot 60^{32}\cdot {\frac {80!}}{2}}\cdot {\frac {24^{80}}{2}}\cdot {\frac {40!\cdot 80!}}{2}}\cdot {\frac{6^{80}}{2}}:\cdot {\2^{40}{2}}:}$

${\displaystyle \sim 10^{561}\,\!}$

2⁵ 5시 30분

피스 카운트[1]
정점 수	32	5색 조각 수	32
가장자리 수	80	4색조 수	0
면 수	80	3색 조각 수	0
세포수	40	2색 조각 수	0
4-Cube 수	10	1색 조각 수	0
5-Cube 수	1	0색 조각 수	0
색칠된 조각 수	32
스티커 수	160

달성 가능한 조합:^[4]

${\displaystyle ={\frac {31!}}{2}}\cdot 60^{31}}}$

${\displaystyle \sim 10^{89}\,\!}$

5시⁵ 15분 4초

피스 카운트[1]
정점 수	32	5색 조각 수	32
가장자리 수	80	4색조 수	160
면 수	80	3색 조각 수	320
세포수	40	2색 조각 수	320
4-Cube 수	10	1색 조각 수	160
5-Cube 수	1	0색 조각 수	32
색칠된 조각 수	992
스티커 수	2,560

달성 가능한 조합:^[4]

${\displaystyle ={\frac {31!}}{2}}\cdot 60^{31}\cdot {\frac {160!}}{2}}\cdot {\frac{12^{160}}{3}}\cdot {\frac {320!}}{24^{80}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {320!}}{8!^{40}}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {{160!}{16!^{10}}}}}}}}}}}}}}}$

${\displaystyle \sim 10^{2075}\,\!}$

5시⁵ 15분

피스 카운트[1]
정점 수	32	5색 조각 수	32
가장자리 수	80	4색조 수	240
면 수	80	3색 조각 수	720
세포수	40	2색 조각 수	1,080
4-Cube 수	10	1색 조각 수	810
5-Cube 수	1	0색 조각 수	243
색칠된 조각 수	2,882
스티커 수	6,250

달성 가능한 조합:^[4]

${\displaystyle {\display}={\frac {32!}}{2}}\cdot 60^{32}\cdot {\frac {80!}}{2}}\cdot{\frac{24^{80}}{2}}\cdot{\frac{160!}}{2}}\cdot {\frac{12^{160}}{3}}\cdot {\frac!\cdot 80!}}{2}}\cdot {\frac{6^{80}}{2}}\cdot {\frac{2^{40}}}}}{{2}}\cdot {\frac {320!}}{24^{80}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {320!}}{24^{80}}}\cdot {\frac {6^{320}:{2}}:\cdot {\frac {240!}{(6!)^{40}}}\cdot {\frac{240}{2}}:\cdot {\frac {320!}{(8!)^{40}}\cdot {\frac{2^{320}}{2}}\cdot {\frac {message!}}{{(12!)^{40}}}\cdot {\frac{2^{11}}{2}}\cdot {\frac {80!}{(8!)^{10}}\cdot {\frac {160!}{{10}}}\cdot \{\frac {240!}}{{(24!)^{10}}\cdot {\frac {320!}}{{(32!)^{10}}}\끝{118}}}$

${\displaystyle \sim 10^{5267}\,\!}$

5시⁵ 30분 6초

피스 카운트[1]
정점 수	32	5색 조각 수	32
가장자리 수	80	4색조 수	320
면 수	80	3색 조각 수	1,280
세포수	40	2색 조각 수	2,560
4-Cube 수	10	1색 조각 수	2,560
5-Cube 수	1	0색 조각 수	1,024
색칠된 조각 수	6,752
스티커 수	12,960

달성 가능한 조합:^[4]

${\displaystyle {\frac{31!}}{2}}\cdot 60^{31}\cdot {\frac {160!}}{2}}\cdot{\frac{12^{160}}{3}}\cdot{\frac {160!}}{2}}\cdot {\frac{12^{160}}{3}}\cdot {\frac {320!}}{24^{80}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {320!}}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {reason!}}{24^{160}}\cdot {\frac {3^{116}}{3}}}{3}\cdot {\frac {320!}}{8!^{40}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {320!}}{8!^{40}}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {960!}{24!^{40}}\cdot {\frac{2^{960}{2}}\cdot {\frac {960!}{24!^{40}}}\cdot {\frac {2^{960}}{2}}\cdot {\frac {640!}{64!^{10}}}\cdot {\frac {960!}{96!^{10}}}\cdot \\{\frac {640!}{64!^{10}}}\cdot {\frac {160!}{16!^{10}}}\cdot {\frac {160!}{16!^{10}}}\end{matrix}}}$

${\displaystyle \sim 10^{11441}\,\!}$

5시⁵ 7분

피스 카운트[1]
정점 수	32	5색 조각 수	32
가장자리 수	80	4색조 수	400
면 수	80	3색 조각 수	2,000
세포수	40	2색 조각 수	5,000
4-Cube 수	10	1색 조각 수	6,250
5-Cube 수	1	0색 조각 수	3,125
색칠된 조각 수	13,682
스티커 수	24,010

달성 가능한 조합:^[4]

${\displaystyle {\display}={\frac {32!}}{2}}\cdot 60^{32}\cdot {\frac {80!}}{2}}\cdot{\frac{24^{80}}{2}}\cdot{\frac{160!}}{2}}\cdot{\frac{12^{160}}{3}}\cdot{\frac {160!}}{2}}\cdot {\frac{12^{160}}{3}}\cdot {\frac!\cdot 40!}}{2}}\cdot {\frac{6^{80}}{2}}\cdot {\frac{2^{40}}}}}{{2}}\cdot {\frac {320!}}{24^{80}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {320!}}{24^{80}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {320!}}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {reason!}}{24^{160}}\cdot {\frac {3^{116}}{3}}}{3}\cdot {\frac {320!}}{24^{80}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {240!}}{6!^{40}}}\cdot \\{240^{240}}{2}}\cdot {\frac!}{12!^{40}}\cdot {\frac{2^{11}}{2}}\cdot {\frac {320!}}{8!^{40}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {240!}}{6!^{40}}}\cdot {\frac {240^}{2}}\cdot {\frac {960!}{24!^{40}}\cdot {\frac{2^{960}{2}}\cdot {\frac {960!}{24!^{40}}\cdot {\frac{2^{960}}{2}}\cdot {\frac!}{12!^{40}}\cdot {\frac{2^{115}{2}}\cdot {\frac {960!}{24!^{40}}\cdot {\frac{2^{960}}{2}}\cdot {\frac {320!}}{8!^{40}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {80!}}{8!^{10}}}\cdot {\frac {240!}{24!{10}}\cdot {\frac {320!}{32!}}}\frac {160!}{16!^{10}}\frac {80!}{8!^{10}}}\cdot \\{\frac {480!}{48!^{10}}}\cdot {\frac {960!}{96!^{10}}}\cdot {\frac {640!}{64!^{10}}}\cdot {\frac {240!}{24!^{10}}}\cdot {\frac {960!}{96!^{10}}}\cdot {\frac {960!}{96!^{10}}}\cdot {\frac {320!}{32!^{10}}}\cdot {\frac {640!}{64!^{10}}}\cdot {\frac {160!}{16!^{10}}}\end{matrix}}}$

${\displaystyle \sim 10^{21503}\,\!}$

매직 큐브 7D

기하학적 형상: 육각형(6D)과 간극형(7D)

안드레이 애스트렐린의 매직 큐브 7D 소프트웨어는 3⁴~5사이즈에서⁷ 최대 7차원 퍼즐을 렌더링할 수 있다.

2016년 5월 현재 3⁶, 3⁷, 4, 5개의⁶⁶ 퍼즐만 풀렸다.^[5]

매직 120 셀

기하학적 형상: 120-셀(헤카토닉오사초론 또는 도데카콘타초론이라고도 함)

120셀은 도데카헤드라 120개로 구성된 4차원 기하학적 형상(4폴리토프)으로, 다시 12개의 펜타곤으로 구성된 3차원 형상이다.120 셀은 큐브의 4-D 아날로그인 테서락트(4-큐브)와 같은 방식으로 도데카헤드론의 4-D 아날로그다.따라서 중력3d에서 나온 4D 120셀 소프트웨어 순차 이동 퍼즐은 도데카헤드론 모양을 한 메가믹스 3D 퍼즐의 4D 아날로그다.

퍼즐은 한 면에 3개의 큐빅으로 이루어진 하나의 사이즈로 만들어지지만 다양한 난이도의 6가지 컬러링 방식으로 만들어진다.풀 퍼즐은 각 셀에 대해 120가지 색상인 다른 색을 요구한다.이 많은 색깔들은 어떤 색조들은 구별하기 매우 어렵다는 점에서 퍼즐의 난이도를 더한다.가장 쉬운 형태는 두 개의 연동형 토리로, 각각의 토러스들은 서로 다른 차원의 큐비즈 링을 형성한다.착색 계획의 전체 목록은 다음과 같다.

• 2파운드의 토리.
• 9-105 4-105 셀.즉, 4-큐브와 같은 착색 방식이다.
• 9단계의 층.
• 12인치 반지.
• 60마일의 항우울제정반대되는 도데카헤드론 세포의 각 쌍은 같은 색이다.
• 120마일의 풀 퍼즐.

컨트롤은 4-D 관점, 셀 크기, 스티커 크기 및 거리, 일반적인 줌 및 회전을 위한 컨트롤이 있는 4-D 매직 큐브와 매우 유사하다.또한, 토리, 4큐브 세포, 층 또는 고리의 선택에 따라 세포 그룹을 완전히 끄는 기능이 있다.

그라비티3d는 해결책의 로그파일을 제공해야 하는 해결사들을 위해 "명예의 전당"을 만들었다.퍼즐은 2017년 4월 현재 12차례나 풀렸다.^[6]

피스 카운트[7]
정점 수	600	4색조 수	600
가장자리 수	1,200	3색 조각 수	1,200
면 수	720	2색 조각 수	720
세포수	120	1색 조각 수	120
4-셀 수	1	0색 조각 수	1
색칠된 조각 수	2,640
스티커 수	7,560

달성 가능한 조합:^[7]

${\displaystyle ={\frac {600!}}{2}}\cdot{\frac {message!}}{2}}\cdot{\frac {message!}}{{2}}\cdot{2^{6}}{6^{6^}}}{2}}\cdot{\12^{600}}{3}}}}}}$

${\displaystyle \sim 10^{8126}\,}$

달성 가능한 조합의 이러한 계산은 수학적으로 입증되지 않았으며 상한으로만 간주될 수 있다.그것의 파생은 모든 "최소한의 변화" 조합을 만드는 데 필요한 알고리즘 집합의 존재를 가정한다.퍼즐 해결사들이 지금까지 해결된 모든 유사한 퍼즐에서 그것들을 찾는데 성공했기 때문에 이러한 알고리즘들이 발견되지 않을 것이라고 추측할 이유는 없다.

3x3 2D 제곱

기하학적 형상: 사각형

2-D 루빅형 퍼즐은 4-D형 퍼즐처럼 물리적으로 구성될 수 없다.^[8]3-D 퍼즐은 3차원에 스티커 없이 구성될 수 있으며, 이는 2-D 퍼즐로 작동하지만, 퍼즐의 진정한 구현은 가상 세계에 남아 있다.여기에 나타난 구현은 그것을 2D 매직 큐브라고 부르는 슈퍼리미날로부터 나온 것이다.

그 퍼즐은 해결책이 아주 사소한 것이기 때문에 해결사들에게는 큰 관심이 없다.대체로 이것은 곡선을 꼬아서 제자리에 놓을 수 없기 때문이다.표준 루빅스 큐브에서 가장 어려운 알고리즘 중 일부는 조각이 정확한 위치에 있지만 올바른 방향은 아닌 그런 반전을 다루는 것이다.고차원적인 퍼즐로 이 비틀림은 겉으로 보기에는 다소 당황스러운 형태를 취할 수 있다.2×2 퍼즐의 난이도를 3×3(동일한 수의 조각을 가지고 있음)과 비교하기만 하면 높은 차원에 트위스트를 일으키는 이 능력은 난이도와 많은 관련이 있으며, 따라서 지금까지 유행하던 루빅큐브 해소에 대한 만족도와도 관계가 있다는 것을 알 수 있다.

피스 카운트[1]
정점 수	4	2색 조각 수	4
가장자리 수	4	1색 조각 수	4
면 수	1	0색 조각 수	1
색칠된 조각 수	8
스티커 수	12

달성 가능한 조합:

$(\displaystyle =4!\,\!=24}$

중심 조각은 서로 상대적인 고정된 방향(표준 3×3×3 큐브의 중심 조각과 정확히 같은 방식으로)이므로 조합 계산에서 계산하지 않는다.

이 퍼즐은 사실 루빅스 큐브의 진정한 2차원 아날로그가 아니다.n차원 퍼즐의 단일 폴리토프에 대한 운영 그룹이 (n – 1)차원 공간에서 (n – 1)차원 폴리토프의 회전으로 정의되는 경우, 그룹의 크기

• 5-115는 4-공간 = 8×6×4 = 192의 4-118의 회전이다.
• 4극은 3-공간 = 6×4 = 24의 3-제곱(제곱)의 회전이기 때문에,
• 3-분할은 2-제곱(제곱)의 회전(2-공간 = 4)인 경우
• 1-공백 = 1-공백의 1-공백의 회전 2-공백에 대하여

즉, 실제 3D 퍼즐과 마찬가지로 이동에 제약을 가하면 2D 퍼즐을 전혀 스크램블할 수 없다.2D Magic Cube에 실제로 주어진 움직임은 반사 작용이다.이 반사 작업은 더 높은차원 퍼즐로 확장될 수 있다.3D 큐브의 경우, 유사한 동작은 얼굴을 제거하고 큐브를 마주보는 스티커로 대체하는 것이다.4-큐브의 경우, 유사작전은 큐브를 제거하고 안쪽으로 교체하는 것이다.

1D 투영

또 다른 대체차원 퍼즐은 데이비드 밴더첼의 매직 큐브 3D에서 달성할 수 있는 관점이다.2D 컴퓨터 화면에 투사된 4-큐브는 일반적인 형태의 n-차원 퍼즐이 (n – 2)차원 공간에 투사된 예다.이것의 3D 아날로그는 반더셀의 프로그램이 할 수 있는 1차원 표현으로 큐브를 투영하는 것이다.

밴더스첼은 아무도 이 퍼즐의 1D 투영법을 풀었다고 주장하지 않는 것에 홀렸다.^[9]그러나, 이 퍼즐에 대한 기록이 보관되지 않기 때문에, 실제로 그것이 풀리지 않은 경우는 아닐 수도 있다.

참고 항목

• 루빅스 큐브 그룹
• 루빅스 큐브 소프트웨어 목록
• 4차원 게임 목록

참조

추가 읽기

• H. J. Kamack과 T. R. Keane, The Rubik Tesseract는 여기에서 온라인으로 이용 가능하며 2008년 12월 25일에 보관되었다.
• 벨레만, D, "루빅의 테세락트", 수학 잡지 65권, 1위(1992년 2월), 수학적 협회 27~36권.
• Pickover, C, 하이퍼스페이스를 통한 서핑, pp120–122, 옥스포드 대학 출판부, 1999.
• Pickover, C, Alian IQ Test, 24장 Dover Publishments, 2001.
• Pickover, C, The Zen of Magic Square, Circles and Stars, pp130–133, 프린스턴 대학 출판부, 2001.
• 2001년 6월, 컴퓨터 큐비스트 데이비드 싱마스터.4D 참조를 포함하여 Singmaster가 관리하는 목록.2008년 6월 19일 검색됨

외부 링크

• 슈퍼리미날
• 중력3d의 D차원 루빅 큐브 구조
• 데이비드 밴더스첼의 3D 매직 큐브