This is a good article. Click here for more information.

천구

Celestial spheres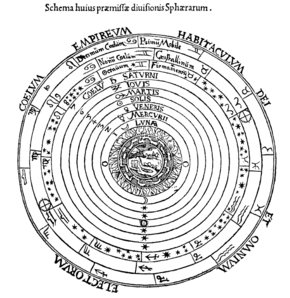
천구와 혼동하지 말 것.
"천공"은 여기서 리다이렉트됩니다.Studio de musique ancienne de Montréal의 앨범은 Heaven Spires를 참조하십시오.
지구중심 천구;피터 아피안의 코스모그래피아 (개미, 1539년)

천구, 또는 천구들은 플라톤, 에우독소스, 아리스토텔레스, 프톨레마이오스, 코페르니쿠스, 그리고 다른 사람들에 의해 개발된 우주론 모델의 근본적인 실체였다.이러한 천체 모형에서, 고정된 별과 행성의 겉으로 보이는 움직임은 마치 오르브에 박힌 보석처럼, 에테르성 투명한 다섯 번째 원소(주석)로 만들어진 회전 구에 포함된 것으로 간주함으로써 설명된다.고정된 별들은 서로 상대적인 위치를 바꾸지 않는다고 믿었기 때문에, 그것들이 하나의 별이 빛나는 [1]구 표면에 있어야만 한다는 주장이 제기되었다.

현대 사상에서는 행성의 궤도는 대부분 빈 공간을 통과하는 행성들의 경로로 보인다.그러나 고대와 중세의 사상가들은 천체의 오목한 부분이 서로 겹치는 두터운 희귀물질의 구라고 여겼으며, 각각은 그 위의 구와 아래의 [2]구와 완전히 맞닿아 있었다.학자들은 프톨레마이오스의 에피사이클을 적용했을 때, 그들은 각 행성 구체가 그들을 [2]수용할 수 있을 정도로 정확히 두껍다고 추정했다.이 중첩된 구체 모형을 천문학적 관측과 결합함으로써 학자들은 태양까지의 거리, 다른 행성들, 그리고 우주의 끝까지의 거리, 약 7300만 마일(1억1700만 킬로미터)[3]에 대해 그 당시에 일반적으로 받아들여진 값을 계산했다.내포된 구체 모형이 태양과 행성에 미치는 거리는 현재 측정된 [4]거리와 크게 다르며, 우주의 크기는 상상할 수 없을 정도로 크고 지속적으로 [5]팽창하는 것으로 알려져 있습니다.

앨버트 반 헬든은 1250년부터 17세기까지 거의 모든 교육받은 유럽인들이 "구체를 둥지로 만들고 거기서 파생된 우주 차원"[6]이라는 프톨레마이오스식 모델에 익숙했다고 제안했습니다.코페르니쿠스의 태양중심 모델을 채택한 후에도, 새로운 버전의 천구 모델이 도입되었고, 행성 구들은 수성, 금성, 지구-달, 화성, 목성, 토성의 이 순서를 따랐다.

천체의 이론에 대한 주류의 믿음은 과학 혁명에서 살아남지 못했다.1600년대 초, 케플러는 행성들이 구에 의해 운반된다는 것을 고려하지 않았지만, 케플러의 행성 운동 법칙에 의해 묘사된 타원 경로를 따라 움직인다고 주장했지만, 계속해서 천체에 대해 논의했다.1600년대 후반, 지구 및 천체 물체의 움직임에 관한 그리스와 중세 이론들은 케플러의 법칙이 물체 사이의 중력에서 어떻게 발생하는지 설명하는 뉴턴의 만유인력의 법칙과 뉴턴 역학에 의해 대체되었다.

역사

천구의 운동 원인에 대한 추가 정보:천체의 역학

구와 원에 대한 초기 아이디어

고대 그리스에서 천체와 고리의 개념은 기원전 [7]6세기 초에 아낙시만데르의 우주론에 처음 등장했다.그의 우주론에서 태양과 달은 모두 응축된 공기의 튜브에 둘러싸인 관 모양의 불 고리에 있는 원형으로 열린 통풍구이다; 이 고리들은 지구를 중심으로 회전하는 전차 같은 바퀴의 테두리를 구성한다.고정된 별들은 또한 그러한 바퀴 테두리 안에 열린 구멍이지만, 별들에는 너무나 많은 바퀴들이 있어서 그들의 연속된 테두리들은 모두 지구를 감싸고 있는 연속적인 구형 껍데기를 형성합니다.이 모든 바퀴 테두리는 원래 지구를 완전히 감싸고 있는 원래의 불덩어리로부터 형성되었고, 그것은 많은 개별 [8]고리로 분해되었다.따라서, 아낙시만더스의 우주론에서는, 태초에 천체 고리가 형성된 구가 있었고, 그 중 일부는 차례로 별 구가 구성되었다.지구에서 볼 때 태양의 고리가 가장 높고 달의 고리가 더 낮으며 별의 구가 가장 낮았다.

아낙시만데르에 이어, 그의 제자 아낙시메네스 (585–528/4)는 별, 태양, 달, 그리고 행성들이 모두 불로 이루어져 있다고 생각했습니다.하지만 별들이 못이나 기둥처럼 회전하는 크리스털 구체에 고정되어 있는 반면, 태양, 달, 행성, 그리고 지구는 모두 그 [9]넓이 때문에 나뭇잎처럼 공중에 떠다닌다.그리고 고정된 별들이 항성권에 의해 완전한 원을 그리며 도는 반면, 태양, 달 그리고 행성들은 별들처럼 지구 아래에서 지는 것과 다시 떠오르는 것 사이에서 회전하는 것이 아니라, 그들은 다시 떠오를 때까지 머리의 중간을 도는 모자처럼 지구 주위를 가로로 돈다.그리고 아낙시만더와는 달리, 그는 고정된 별들을 지구에서 가장 멀리 떨어진 지역으로 내몰았다.아낙시메네스의 우주의 가장 영구적인 특징은 별이 단단한 틀에서처럼 결정구 위에 고정된다는 개념이었고, 이것은 코페르니쿠스와 케플러에 이르기까지 우주론의 기본 원리가 되었다.

아낙시메네스 이후, 피타고라스, 크세노파네스, 파르메니데스 모두 우주가 [10]구형이라고 생각했다.그리고 기원전 4세기 플라톤의 티마이오스는 우주의 본체가 가장 완벽하고 균일한 형태로 만들어졌다고 주장했습니다. 고정된 [11]별들을 포함한 구체의 것입니다.그러나 이 행성들은 아낙시만더의 우주론에서처럼 바퀴 테두리가 아닌 회전하는 띠나 고리로 설정된 구형 물체라고 가정했다.

행성 구체의 출현

띠 대신 플라톤의 제자 유독수스는 모든 행성에 동심원 구를 사용하는 행성 모형을 개발했는데, 달과 태양 모형에는 각각 3개의 구가 있고 나머지 5개의 행성 모형에는 각각 4개의 구가 있어 [12][13]총 26개의 구를 만들었다.칼리포스는 태양, 달, 수성, 금성, 화성 모형에는 5개의 구를 사용하고 목성과 토성 모형에는 4개의 구를 유지하여 [13]총 33개의 구를 만드는 등 이 체계를 수정했다.각각의 행성은 그들만의 특별한 구들 중 가장 안쪽에 붙어있다.에우독수스와 칼립푸스의 모형은 행성 운동의 주요 특징을 정성적으로 묘사하고 있지만, 그들은 이러한 움직임을 정확하게 설명하지 못하기 때문에 양적 [14]예측을 제공할 수 없다.그리스 과학 역사가들은 전통적으로 이 모델들을 단지 기하학적 [15][16]표현이라고 여겼지만, 최근의 연구들은 이 모델들이 물리적으로[17] 실재하거나 이 [18]문제를 해결하기 위한 제한된 증거에 주목하면서 판단을 보류하는 것을 제안했다.

그의 형이상학에서, 아리스토텔레스는 에우독소스의 수학적 모델에 기초해 구체의 물리적 우주론을 발전시켰다.아리스토텔레스의 완전히 발달된 천체 모형에서, 구면 지구는 우주의 중심에 있고 행성들은 통합된 [19]행성계를 형성하는 47개 또는 55개의 서로 연결된 구들에 의해 움직인다. 반면 에우독소스와 칼립포스의 모형에서는 각 행성의 개별 구들은 다음 행성의 구들과 연결되어 있지 않았다.아리스토텔레스는 정확한 구(球)의 수와 이동자의 수는 천문학적 조사에 의해 결정된다고 말하지만, 그는 외구의 움직임에 대항하기 위해 에우독소스와 칼립포스가 제안한 구(球)에 추가 구를 추가했다.아리스토텔레스는 이 구체들이 변하지 않는 다섯 번째 요소인 에테르로 이루어져 있다고 생각한다.이 동심원 구들 각각은 그 자체의 신에 의해 움직인다. 즉, 불변의 신성한 흔들림 없이 움직이는 신이며,[20] 그들은 단지 그것에 의해 사랑받기 때문에 그 영역을 움직인다.

금성, 화성, 목성, 토성 구체의 프톨레마이오스 모형으로 에피사이클, 편심 변위점 및 등각점.게오르그 폰 포이어바흐, 테오리카에 노바에 플라네타룸, 1474.

그의 알마게스트에서, 천문학자 프톨레마이오스는 별과 행성의 움직임에 대한 기하학적 예측 모델을 개발했고 그의 행성 [21][22][23][24]가설에서 그것들을 우주의 통일된 물리적 모델로 확장했습니다.에크트릭스와 에피사이클을 사용함으로써,[25] 그의 기하학적 모델은 우주의 초기 동심원 구형 모델에서 보여졌던 것보다 더 큰 수학적 세부사항과 예측 정확도를 달성했습니다.프톨레마이오스의 물리적 모형에서, 각각의 행성은 두 개 이상의 [26]구에 포함되어 있지만, 프톨레마이오스는 그의 행성 가설의 제2권에서 제1권에서와 같이 구가 아닌 두꺼운 원형 조각을 묘사했다.한 구/슬라이스는 지구에서 중심 오프셋이 있는 배변이고, 다른 구/슬라이스는 배변에 내장된 에피사이클이며, 유성/슬라이스는 에피사이클릭 구/슬라이스에 [27]내장되어 있습니다.프톨레마이오스의 둥지 구 모형은 우주의 일반적인 치수를 제공했는데, 토성의 가장 큰 거리는 지구의 19,865배이고 고정된 별의 거리는 적어도 20,000개의 지구 반지름이다.[26]

행성 구들은 달의 구, 수성, 금성, 태양, 화성, 목성, 토성의 구 순으로 우주의 중심에 있는 구형 정지 지구로부터 바깥쪽으로 배열되었다.좀 더 상세한 모형에서는 일곱 개의 행성 구가 그 안에 다른 보조 구를 포함하고 있었다.행성구에는 고정된 별들을 포함하는 항성구가 뒤따랐다; 다른 학자들은 분점의 세차운동을 설명하기 위해 9번째 구를, 추분의 추정된 두려움을 설명하기 위해 10번째 구를, 그리고 [28]황도의 변화하는 경사도를 설명하기 위해 11번째 구를 추가했다.고대에는 하위 행성들의 순서가 보편적으로 합의되지 않았다.플라톤과 그의 추종자들은 그들에게 달, 태양, 수성, 금성을 주문했고, 그리고 나서 상부 [29][30]구에 대한 표준 모델을 따랐다.다른 사람들은 수성과 금성의 구체의 상대적인 위치에 대해 동의하지 않았다: 프톨레마이오스는 두 구를 모두 수성 위에 놓고, 다른 사람들은 두 구를 모두 태양 위에 놓고; 알 비트루지와 같은 몇몇 중세 사상가들은 금성의 구를 태양 아래에 놓았다.[31]

중세 시대

천문학적 논의

11세기 후반 De Natura Reum의 베데에서 7개의 천구 안에 있는 지구

무슬림 천문학자 알-파르한으로 시작하는 일련의 천문학자들은 별과 행성 구와의 거리를 계산하기 위해 둥지 구체의 프톨레마이오스 모델을 사용했다.알파르한의 별까지의 거리는 20,110 지구 반지름으로, 지구의 반지름은 3,250 마일(5,230 킬로미터)이라고 가정했을 때, 65,357,500 마일(105,182,700 킬로미터)[32]이 되었다.프톨레마이오스의 알마게스트에 대한 소개, 타실 알-마지스티는 타비트 이븐 코라에 의해 쓰여진 것으로 믿어져,[33] 천구까지의 프톨레마이오스의 거리에 대한 작은 변화를 보여주었다.그의 Zij에서, 알-바탄은 둥지 구체의 모형으로 행성까지의 거리에 대한 독립적인 계산을 제시했는데, 그는 이것이 프톨레마이오스 이후에 쓴 학자들 때문이라고 생각했다.그의 계산은 [34]별까지의 19,000 지구 반지름을 산출했다.

밀레니엄이 바뀔 무렵, 아랍의 천문학자이자 박식가인 이븐 알-헤이탐은 프톨레마이오스의 지구중심 모델을 내포된 구에 대해 발전시켰다.이 개념이 프톨레마이오스의 행성 가설과 유사함에도 불구하고, 알-헤이담의 발표는 충분히 세부적으로 차이가 있어 [35]개념의 독립적인 발전을 반영한다는 주장이 제기되어 왔다.이븐 알-헤이담은 또한 그의 광학 서 15장부터 16장까지에서 천구는 고체 [36]물질로 구성되어 있지 않다고 말했다.

12세기 말쯤, 스페인의 이슬람 천문학자 알 비트루지는 동서로 다른 속도로 움직이는 순수한 동심원 구체의 아리스토텔레스식 틀을 사용하여 프톨레마이오스의 에피사이클과 에센트릭스가 없는 행성들의 복잡한 움직임을 설명하려고 했다.이 모형은 예측 천체 [37]모형보다 훨씬 덜 정확했지만, 후기 유럽 천문학자들과 [38][39]철학자들에 의해 논의되었다.

13세기에 천문학자 알-우르시는 프톨레마이오스의 둥지 구 체계에 근본적인 변화를 제안했다.그의 키타브 알-하야에서, 그는 그가 다시 결정한 매개변수를 사용하여 행성들의 거리를 다시 계산했다.태양의 거리를 지구 반지름 1,266으로 간주하여, 그는 금성의 구를 태양의 구 위에 놓도록 강요받았다; 더 정교하게, 그는 구들의 두께에 행성의 직경을 더했다.그 결과, 그의 둥지 구상 모형은 지구 반지름 140,[34]177개의 별들의 구를 가지고 있었다.

비슷한 시기에 유럽 대학의 학자들은 아리스토텔레스의 재발견된 철학과 프톨레마이오스의 천문학의 함의를 다루기 시작했다.천문학자들과 인기 작가들 모두 우주의 [40]차원에 대한 내포된 구체 모형의 의미를 고려했다.노바라의 입문 천문서인 Theoryica planetarum의 캄파누스는 지구로부터의 다양한 행성의 거리를 계산하기 위해 둥지 구 모형을 사용했는데, 그는 이를 지구 반지름 22,612 또는 73,387,747로 제시했다. 100평방킬로미터입니다.[41][42]로저 베이컨은 그의 작품에서 알-파르한의 지구 반지름 20,110 마일, 즉 65,357,700 마일까지의 거리를 인용했는데, 여기서부터 그는 우주의 둘레를 410,818,5173.[43]7마일로 계산했다.이 모델이 물리적 현실을 나타낸다고 생각되었다는 분명한 증거는 베이컨의[44] 작품인 Opus Majus와 인기 있는 중세 영어인 South English Legendary에서 발견된 가장 높은 별 [45][46]천국에 도달하는 데 8,000년이 걸린다는 설명입니다.내포된 구체 모형에서 파생된 우주의 치수에 대한 일반적인 이해는 모세 마이모니데스의 히브리어, 메츠의 고수인의 프랑스어, 그리고 단테 알리기에리의 [47]이탈리아어 발표를 통해 더 많은 청중에게 다가갔다.

철학적, 신학적 논의

철학자들은 그러한 수학적 계산보다는 천체의 본질, 창조된 자연에 대한 드러난 설명과 그들의 관계, 그리고 그들의 움직임의 원인에 더 관심이 있었다.

아디 세티아는 12세기 이슬람 학자들 사이에서 벌어진 논쟁을 파크르 알딘 알 라지의 해설을 바탕으로 천체가 실재하는지, 구체적인 물리적 물체인지, 아니면 "단순히 여러 별과 행성에 의해 추적된 천체의 추상적인 원들"인지에 대한 논평을 바탕으로 묘사하고 있다.세티아는 대부분의 학자들과 천문학자들이 "별들이 도는 단단한 구체"라고 말했고 이 관점은 천체의 궤도에 관한 코란 시들의 명백한 감각에 더 가깝다고 지적했다.하지만, 알-라지는 이슬람 학자 다하크와 같은 몇몇 사람들이 그들을 추상적이라고 여겼다고 말한다.알-라지 자신은 결정을 내리지 못했다. "사실, 하늘의 특징을 확인할 수 있는 방법은 [신성한 계시 또는 예언적 전통에 대한] 권위 외에는 없다."Setia게 결론을 내리고 있다."Thus이 al-Razi(고 다른 이들 전 후 그를), 천문학적인 모델들을 위하여, 전력 회사 또는 하늘을 주문해서 결여를 건전한 합리적인 교정에 있고, 천상의 현실에 대한 묘사와 설명을 우려하고 있지 않으므로 지적 헌신 그들에게 하는 한에 있어서는 만들어질 수 있는 설립되지 않는 것 같다."[48]

기독교와 이슬람 철학자들은 프톨레마이오스의 체계를 수정하여 움직이지 않는 가장 바깥 지역, 즉 하느님과 [49]모든 선택된 사람들의 거주지로 확인되게 된 엠피리아 천국을 포함시켰다.중세 기독교인들은 별의 구를 성경에 나오는 굳은살과 동일시했고,[50] 때때로 창세기에 따라 굳은살 위에 보이지 않는 물층을 두었다.천사가 살고 있는 바깥의 구체가 몇몇 [51]기록에서 나타났다.

과학사학자 에드워드 그랜트는 중세 스콜라 철학자들이 일반적으로 천체를 3차원 또는 연속적인 의미에서 견고하다고 생각했지만, 대부분은 단단한 의미에서 견고하다고 생각하지 않았다는 증거를 제시해 왔다.천체가 일종의 연속적인 [52]유체로 만들어졌다는 것이 일치된 의견이었다.

21세기 후반, 무타칼림 아두드 알딘 알-이지(1281–1355)는 모든 물리적 영향은 자연적 [53]원인이 아닌 신의 의지에 의해 직접 발생한다고 주장한 원자론의 아슈아리 교리에 따라 균일하고 원형의 운동 원리를 거부했다.그는 천체가 "상상적인 것"이며 "거미줄보다 더 약한 것"[54]이라고 주장했다.그의 견해는 알-주르자니 (1339–1413)에 의해 이의를 제기되었는데, 그는 천체가 외부적인 현실을 가지고 있지 않더라도, 그들은 정확하게 상상되고 실제[[54]외부]에 부합하는 것이라고 주장했다.

중세 천문학자들과 철학자들은 천체의 움직임의 원인에 대한 다양한 이론을 발전시켰다.그들은 그것들이 만들어졌다고 생각되는 물질, 천체의 지능과 같은 외부 운동가, 그리고 원동력이나 감명받은 힘과 같은 내부 운동가들의 관점에서 구체의 움직임을 설명하려고 시도했다.일부 모델은 속도, 추진력 및 [55]저항과 관련된 정량적 분석을 포함했지만, 이러한 모델의 대부분은 정성적이었다.중세 말기에 이르러, 유럽의 공통된 견해는 천체가 [56]계시의 천사와 동일시되는 외부 지성에 의해 움직인다는 것이었다.모든 하위 영역에 영향을 미치는 매일의 움직임과 함께 움직였던 가장 바깥쪽의 움직이는 구체는 움직이지 않는 이동자, 즉 신과 동일시된 원동자에 의해 움직였다.각각의 하부 구는 지능이라고 불리는 [57]하위 영적 이동자에 의해 움직였습니다.

르네상스

토마스 디게스의 1576년 코페르니쿠스 천체 중심 모델

16세기 초에 니콜라우스 코페르니쿠스는 지구를 중심에서 태양 쪽으로 이동시킴으로써 천문학 모델을 획기적으로 개혁했지만, 그는 그의 위대한 작품을 "천구의 회전에 대하여"라고 불렀다.비록 코페르니쿠스가 우주의 물리적 성질을 자세히 다루지는 않지만, 그의 몇 가지 암시는 그의 전임자들처럼 그가 비고체적인 [58]천체를 받아들였다는 것을 분명히 한다.코페르니쿠스는 아홉 번째와 열 번째 구를 거부하고, 지구 주위에 달의 구를 배치하고, 태양을 그 구에서 우주의 중심으로 이동시켰다.행성 궤도들은 다음과 같은 순서로 우주의 중심을 돌았다.수성, 금성, 지구와 달의 구를 포함하는 거대한 구, 그리고 화성, 목성, 토성의 구.마침내 그는 [59]정지해 있던 별들의 8번째 구를 유지했습니다.

영국의 연감 제작자인 토마스 디지스는 칼레스티올 오르브에 대한 그의 Perfit Description of the Caelestiall Orbes… (1576년)에서 새로운 우주 시스템의 구들을 묘사했다.여기서 그는 "궤도"를 새로운 코페르니쿠스적 순서로 배열하여 "죽음의 지구", "지구, 4개의 고전적 요소, 달을 운반하기 위해 하나의 구를 확장하고 별의 구를 무한히 확장하여 모든 별을 감싸고 "위대한 신의 궁정, 선택자의 습관, 그리고 실리스탈리 아겔"의 역할을 했다.es.[60]

코페르니쿠스의 의견에 따른 요하네스 케플러의 천체 및 그 사이의 공간도(미스테리움 코스모그래픽, 제2판, 1621년)

16세기에, 프란체스코 파트리지, 안드레아 치살피노, 피터 라무스, 로버트 벨라르미네, 지오르다노 브루노, 제로니모 무뇨즈, 미카엘 네안데르, 장 페나, 크리스토프 로트만을 포함한 많은 철학자, 신학자, 천문학자들이 [61]천체의 개념을 포기했다.로스만은 1585년 혜성을 관측한 결과, 관측된 시차가 없다는 것은 혜성이 토성 밖에 있다는 것을 나타내는 반면, 관측된 굴절의 부재는 천구가 공기와 같은 물질이라는 것을 의미하므로 행성 구체가 존재하지 [62]않는다고 주장했다.

티코 브라헤는 1587년부터 1585년까지 일련의 혜성에 대한 로트만의 논의와 행성 오르브를 통과한 미카엘 마에스트린의 1577년 혜성에 대한 표로 된 거리에 의해 도움을 받아 "천체의 구조는 매우 유동적이고 단순하다"는 결론을 내리게 되었다[63].티코는 하늘을 "경직하고 불침투성 물질로 만들어진 다양한 오브"로 나눈 "매우 많은 현대 철학자들"의 견해에 반대했다.에드워드 그랜트는 코페르니쿠스 이전에 단단한 천체를 비교적 적게 믿었고, 이 생각은 [64][65]1542년 코페르니쿠스의 De Revolutionbus의 출판과 1588년 Tycho Brahe의 혜성 연구 출판 사이에 처음으로 보편화되었다고 결론지었다.

그의 초기 미스테리움 코스모그래픽에서, 요하네스 케플러는 행성들의 거리와 코페르니쿠스 체계에 의해 암시된 행성들 사이의 간격에 대해 고려했고, 이것은 그의 전 스승인 마이클 마에스트린이 [66]언급했습니다.케플러의 플라톤 우주론은 큰 간격을 5개의 플라톤 다면체로 메웠는데, 이 다면체는 구의 측정된 천문학적 거리를 [67][page needed]설명했습니다.케플러의 성숙한 천체 물리학에서, 구들은 초기 아리스토텔레스의 천체 물리학의 회전하는 물리적 오르브라기보다는 각 행성 궤도를 포함하는 순수 기하학적 공간 영역으로 간주되었습니다.따라서 각 행성의 궤도의 이심률은 천구의 안쪽과 바깥쪽 한계 반지름과 두께를 정의했습니다.케플러의 천체역학에서, 행성 운동의 원인은 태양 자체의 동기에 [68]의해 회전하는 태양이었다.하지만, 움직이지 않는 항성구는 케플러의 우주론에서 물리적 천구의 영구적인 잔해였다.

문학적·시각적 표현

"중세의 우주는 유한하기 때문에, 형태, 완벽한 구형의 형태를 가지고 있고, 그 안에 질서 있는 다양성을 포함하고 있습니다…"
"구들은... 정신이 쉴 수 있는 대상을 우리에게 제시하며, 그 위대함에 압도적이지만 그 조화에는 만족합니다."

C. S. Lewis, The Discarded Image, p. 99.

단테와 베아트리체는 구스타브 도레의 삽화부터 신 희극 파라디소 칸토 28행 16~39행까지 가장 높은 천국을 바라봅니다.

키케로의 스키피오의 꿈에서 늙은 스키피오 아프리카누스는 지구와 로마 제국이 하찮아지는 것에 비해 천체를 통한 등정을 묘사한다.로마 작가 마크로비우스의 스키피오의 꿈에 대한 해설은 하늘의 질서에 대한 다양한 학파에 대한 논의를 포함하였고, 초기 [69]중세에 걸쳐 천구에 대한 생각을 확산시키는데 많은 기여를 했다.

니콜 오렘, Le livre du Ciel et du Monde, 파리, BnF, Manuscrits, F. 565, f. 69, (1377).

일부 중세 후기 인물들은 신이 중심에 있고 지구가 주변에 있는 영적 평면에서 천체의 물리적 질서는 그들의 질서와 반대라고 언급했다.14세기 초에 단테는 그의 신 희극의 파라디소에서 신을 [70]우주의 중심에 있는 빛으로 묘사했다.여기서 시인은 육체적 존재를 넘어 엠피리언 천국으로 올라갑니다. 그곳에서 그는 신과 대면하고 신과 인간의 본성을 모두 이해할 수 있습니다.세기의 후반, 니콜 오렘의 후원자인 찰스 5세를 위해 제작된 아리스토텔레스의 드 카엘로를 번역하고 해설한 니콜 오렘의 Le livre du Ciel et du Monde의 조명자는 같은 모티브를 사용했다.그는 달이 지구에 가장 가깝고 별이 가장 높은 전통적인 순서로 구를 그렸지만, 구들은 아래로 오목한 것이 아니라 신을 중심으로 위쪽으로 오목한 것이 [71]지구를 중심으로 했다.이 그림 아래 오레스메는 시편을 인용하여 "하늘은 신의 영광을 선포하고 굳건함은 그의 [72]작품을 보여준다"고 말한다.

16세기 후반의 포르투갈 서사시 루시아드는 천체를 [73]신이 건설한 "우주의 위대한 기계"로 생생하게 묘사한다.탐험가 Vasco da Gama는 기계 모형 형태로 천체를 보여준다.키케로의 표현과는 달리, 다 가마의 구 관광은 엠피리언에서 시작해서 지구를 향해 안쪽으로 내려가고, 지구 왕국의 영역과 분할에 대한 조사로 절정에 달하며, 따라서 신성한 계획에서 인간 행위의 중요성을 확대한다.

「 」를 참조해 주세요.

메모들

  1. ^ 그랜트, 행성, 별, 오브, 페이지 440
  2. ^ a b 린드버그, 서양과학의 시작, 페이지 251
  3. ^ Van Helden, Measuring the Universe, 페이지 28-40.
  4. ^ 그랜트, 행성, 별, 오르브, 437-8페이지.
  5. ^ Van Helden, 우주 측정, 3페이지
  6. ^ Van Helden, Measuring the Universe, 37, 40페이지
  7. ^ Samos 1913/97 옥스포드 대학 출판/샌드파이퍼 북스사의 히스의 아리스타르쿠스 제4장 참조; Popper's The World of Parmenides Routledge 1998 페이지 11 참조
  8. ^ 히쓰 따오기 pp26–8
  9. ^ 사모스의 1913년 히스의 아리스타르코스 5장을 참조하라.
  10. ^ 크세노파네스와 파르메니데스의 구면 우주론은 히쓰 따오기 7장과 9장, 포퍼 따오기 2장과 3장을 각각 참조한다.
  11. ^ F. M. 콘포드, 플라톤의 우주론: 플라톤의 티마이우스, 54-7페이지
  12. ^ Neugebauer, 고대 수학 천문학사, 제2권, 677-85페이지.
  13. ^ a b 로이드, "천상의 이상", 페이지 173
  14. ^ Neugebauer, 고대 수학 천문학사, 제2권, 677-85페이지.
  15. ^ 드레이어, 행성계의 역사, 90-1, 121-2페이지
  16. ^ 로이드, 아리스토텔레스, 150페이지
  17. ^ 래리 라이트, "에우독서스의 천문학:기하학 또는 물리학,"과학의 역사와 철학 연구, 4(1973년): 165-72.
  18. ^ G. E. R. Lloyd, "현상의 구함", 고전 분기, 28(1978): 페이지 219에서 202~222.
  19. ^ 아리스토텔레스, 형이상학 1073b1–1074a13, 882–883페이지, The Basic Works of Aristeles Richard McKeon, ed., 2001년 현대 도서관
  20. ^ 아리스토텔레스 형이상학 1072b4는 "그러면, 마지막 원인은 사랑받음으로써 움직임을 만들어내지만, 다른 모든 것은 감동에 의해 움직인다"고 말했다.
  21. ^ Neugebauer, 고대 수학 천문학사, 111-12페이지, 148
  22. ^ Pedersen, 초기 물리 및 천문학, 87페이지
  23. ^ 크로, 세계론, 페이지 45, 49-50, 72,
  24. ^ 린튼, 에우독수스에서 아인슈타인으로, 페이지 63~64, 81.
  25. ^ Taliaferro, 번역자의 알마게스트 입문, p,1, Dreyer, 행성계의 역사, 페이지 160,167.
  26. ^ a b Neugebauer, 고대 수학 천문학사, 제2권, 917–926페이지.
  27. ^ 안드레아 머셜, "프톨레마이오스의 행성운동 물리적 가설의 구조와 기능", 천문학사 저널 26(1995): 33-61.
  28. ^ 프란시스 R.존슨, "말로우의 제국주의 천국", ELH, 12(1945): 35-44, 페이지 39
  29. ^ 브루스 S.Eastwood, Ordering the Heavel: Carolingian Renaissance의 로마 천문학과 우주론, (Leiden: Bril) 2007, 36-45페이지
  30. ^ 그의 혁명서 Bk1.10 코페르니쿠스는 플라톤의 추종자들이 수성과 금성의 궤도를 태양보다 높게 둔 경험적 이유를 주장했는데, 그것은 만약 그들이 태양에 준태양이라면, 그들은 기껏해야 반구처럼 보일 뿐이고, 때로는 태양을 가릴 수도 있기 때문이다.f 서방 세계 16 프톨레마이오스-코페르니쿠스-케플러)
  31. ^ al-Birrujī. (1971) 천문학의 원리에 대하여, 7.159-65, 번역.버나드 R.골드스타인, 제1권, 페이지 123-5.뉴헤이븐: 예일 대학교.Pr. ISBN0-300-01387-6
  32. ^ Van Helden, Measuring the Universe, 페이지 29-31.
  33. ^ Van Helden, Measuring the World, 31페이지
  34. ^ a b Van Helden, Measuring the Universe, 31-2페이지.
  35. ^ Langermann, Y. Tzvi (1990). Ibn al Haytham's on the Configuration of the World. New York: Garland Publishing. pp. 11–25.
  36. ^ 를 클릭합니다Rosen, Edward (1985). "The Dissolution of the Solid Celestial Spheres". Journal of the History of Ideas. 46 (1): 13–31 [19–20, 21]. doi:10.2307/2709773. JSTOR 2709773..
  37. ^ Goldstein, Bernard R. (1971). Al-Bitrūjī: On the Principles of Astronomy. Vol. 1. New Haven: Yale University Press. pp. 40–5.
  38. ^ Goldstein, Al-Bitruj,, 6페이지
  39. ^ 그랜트, 행성, 별, 오르브, 563–6페이지.
  40. ^ 그랜트, 행성, 별, 오르브, 433–43페이지.
  41. ^ 그랜트, 행성, 별, 오르브, 434-8페이지.
  42. ^ Van Helden, Measuring the Universe, 페이지 33-4.
  43. ^ Van Helden, Measuring the World, 36페이지
  44. ^ Van Helden, Measuring the Universe, 페이지 35
  45. ^ 루이스, 폐기된 이미지, 97-8페이지.
  46. ^ Van Helden, Measuring the World, 페이지 38
  47. ^ Van Helden, Measuring the Universe, 37-9페이지.
  48. ^ Adi Setia (2004), "Fakhr Al-Din Al-Razi on Physics and the Nature of the Physical World: A Preliminary Survey", Islam & Science, 2, retrieved 2 March 2010
  49. ^ 그랜트, 행성, 별, 오르브, 382–3페이지.
  50. ^ 린드버그, 서양과학의 시작, 249-50페이지.
  51. ^ 린드버그, 서양과학의 시작, 250페이지
  52. ^ 그랜트, 행성, 별, 오르브, 328–30페이지.
  53. ^ Huff, Toby (2003). The Rise of Early Modern Science: Islam, China, and the West. Cambridge University Press. p. 175. ISBN 978-0-521-52994-5.
  54. ^ a b 페이지 55~57 /
  55. ^ 그랜트, 행성, 별, 오브, 541페이지
  56. ^ 그랜트, 행성, 별, 오브, 페이지 527
  57. ^ 그랜트, 행성, 별, 오르브, 526-45페이지.
  58. ^ 니콜라스 자딘, "코페르니쿠스 오르브의 의미", 천문학사 저널, 13 (1982): 168–94, 페이지 177–78.
  59. ^ Hilderich von Varel(Edo Hildericus), Propositiones Cosmographicae de Globi Terreni Dimensione(프랑크푸르트 d.Oder, 1576)는 Peter Barker와 Bernard R에서 인용했다.골드스타인, "16세기 천문학의 현실주의와 기구주의: 재평가", 과학 6.3(1998): 232–58, 페이지 242–23.
  60. ^ 코일, 닫힌 세계에서, 페이지 28-30.
  61. ^ 마이클 A.그라나다, "티코는 1586년 이전에 천체를 없앴는가?", 천문학사 저널, 37 (2006): 126-45, 페이지 127-29.
  62. ^ 버나드 R.Goldstein과 Peter Barker, "천구 해체에 있어서의 Rothmann의 역할", 영국 과학사 저널, 28(1995): 385–403, 페이지 390–91.
  63. ^ 마이클 A.그라나다, "티코는 1586년 이전에 천체를 없앴는가?", 천문학사 저널, 37 (2006): 126-45, 페이지 132-38.
  64. ^ 그랜트, "천체 오르브", 페이지 185-86.
  65. ^ 그랜트, 행성, 별, 오르브, 345-48페이지.
  66. ^ '마이클 마에스트린의 미스터리'
  67. ^ 필드, 케플러의 기하학적 우주론.
  68. ^ 요하네스 케플러, 코페르니쿠스 천문학의 대명사, 제1권, 4.2.3권, 514–15페이지 (1630)
  69. ^ 마크로비우스, 스키피오의 꿈에 대한 해설, 윌리엄 해리스 스탈 옮김, 뉴욕: 컬럼비아 대학교.1952년 박사; 구순에 대해서는 162-165페이지를 참조한다.
  70. ^ C. S. Lewis, 폐기된 이미지: 케임브리지 중세와 르네상스 문학 입문:케임브리지 대학교박사, 1964년, 페이지 116. ISBN 0-521-09450-X.
  71. ^ 니콜 오렘, "Le livre du Ciel et du Monde", 1377은 2007년 6월 2일을 회수했다.[1]
  72. ^ P. 18:2. 니콜 오레스메에서 인용, Le livre du ciel et du monde, A, D에 의해 편집 및 번역되었습니다.메누트와 A. J. 데노미, 매디슨:위스콘신 대학교 박사, 1968년, 282~283페이지
  73. ^ Luiz Vaz de Cameses, The Lusiads, 랜데그 화이트 옮김옥스포드 대학 출판부, 2010.

참고 문헌

  • 아리스토텔레스 형이상학, '아리스토텔레스 기본 저작물' 리처드 맥킨 (에드) 현대 도서관, 2001
  • Clagett, 위스콘신 중세대학 기계학 마셜 사이언스 1959 출판사
  • 코헨, I.B. & Whitman, A. Principia University of California Press 1999 프레스
  • Cohen & Smith (eds) Campbridge Companion to Newton CUP 2002
  • 코페르니쿠스, 니콜라우스, 서양의 대저서: 16 프톨레마이오스 코페르니쿠스 케플러 브리태니커사 1952
  • Crowe, Michael J. (1990). Theories of the World from Antiquity to the Copernican Revolution. Mineola, NY: Dover Publications, Inc. ISBN 978-0-486-26173-7.
  • 뒤엠, 피에르"물리학의 역사"카톨릭 백과사전.제12권뉴욕: Robert Appleton Company, 1911. 2008년 6월 18일 <http://www.newadvent.org/cathen/12047a.htm>.
  • 뒤엠, 피에르Le Systéme du Monde: Histoire des consumologiques de Platon copern Copernic, 10권, 파리:헤르만, 1959년
  • 뒤엠, 피에르중세 우주론: Theorys of Infinity, Place, Time, Void, and Multiple of Worlds (인피니티, 장소, 시간, 보이드 및 복수 세계 이론) Le Systéme du Monde에서 발췌, 시카고의 Roger Ariew에 의해 번역 및 편집되었습니다.시카고 대학교 출판부, 1987년 ISBN 0-226-16923-5
  • Dreyer, John Louis Emil (2007) [1905]. History of the Planetary Systems from Thales to Kepler. New York, NY: Cosimo. ISBN 978-1-60206-441-6.
  • Eastwood, Bruce, "기독교 라틴 유럽의 천문학 c. 500–c. 1150", 천문학사 저널, 28 (1997) : 235–258.
  • Eastwood, Bruce, Order the Heavening: 카롤링거 르네상스의 로마 천문학과 우주론, Leiden: Bril, 2007.ISBN 978-90-04-16186-3.
  • Eastwood, Bruce and Gerd Grahohoff, 중세 유럽의 로마 천문학을 위한 행성도, ca. 800–1500, 미국철학회 거래, 제94권, 3부, 필라델피아, 2004.ISBN 0-87169-943-5
  • 필드, J. V. 케플러의 기하학적 우주론.시카고:시카고 대학 출판부, 1988년 ISBN 0-226-24823-2
  • Golino, Carlo(에드), Galileo Repraise, 캘리포니아 대학 출판부 1966
  • Grant, Edward, "Celestial Orbs in the Latin Middle Age", Isis, 78(1987): 153-73. The Scientific Enterprise in Attiates and Middle Age, Ed.에 전재.시카고 대학교 박사, 2000년ISBN 0-226-74951-7
  • Grant, Edward, Planets, Stars 및 Orb: 중세 코스모스, 1200–1687, 케임브리지:케임브리지 대학교1994년 박사ISBN 0-521-56509-X
  • 그랜트, 에드워드, 중세 현대과학 재단, 캠브리지:케임브리지 대학교1996년 박사ISBN 0-521-56762-9
  • Grasshoff, Gerd (2012). "Michael Maestlin's Mystery: Theory Building with Diagrams". Journal for the History of Astronomy. 43 (1): 57–73. Bibcode:2012JHA....43...57G. doi:10.1177/002182861204300104. S2CID 117056401.
  • 진저리치, 오웬 천국의 눈, 1993년 미국물리연구소
  • Hutchins, Robert Maynard; Adler, Mortimer J., eds. (1952). Ptolemy, Copernicus, Kepler. Great Books of the Western World. Vol. 16. Chicago, Ill: William Benton.
  • 히스, 토마스, 사모스 옥스포드 대학 출판/샌드파이퍼 북스사의 아리스타르쿠스. 1913/97
  • R.A. Jarrell, Taton & Wilson의 Tycho Brahe의 동시대인 (eds)1989
  • Koyré, Alexandre, Galileo Studies (번역자 Mepham) Harvester Press 1977 ISBN 0-85527-354-2
  • Koyré, Alexandre (1957). From the Closed World to the Infinite Universe. Forgotten Books. ISBN 978-1-60620-143-5.
  • 케플러, 요하네스, 코페르니쿠스 천문학의 대명사 (Bks 4 & 5), 서양의 위대한 책에 출판되었다: 16 프톨레마이오스 코페르니쿠스 케플러, 브리태니커 백과사전 1952.
  • 루이스, C.S., 폐기된 이미지: 케임브리지 중세와 르네상스 문학 입문:케임브리지 대학교 출판부 1964 ISBN 0-521-09450-X
  • Lindberg, David C. (1992). The Beginnings of Western Science. Chicago: University of Chicago Press. ISBN 978-0-226-48231-6.
  • 린드버그, 데이비드 C.(ed.) 시카고 중세 과학:1978년 시카고 대학교 박사ISBN 0-226-48233-2
  • Linton, Christopher M. (2004). From Eudoxus to Einstein—A History of Mathematical Astronomy. Cambridge: Cambridge University Press. ISBN 978-0-521-82750-8.
  • 로이드, G.E.R., 아리스토텔레스: 그의 사상의 성장과 구조, 페이지 133–153, 케임브리지:케임브리지 대학교1968년 박사ISBN 0-521-09456-9.
  • 로이드, G.E.R. "천상의 이상:아마추어 천문학자 아리스토텔레스" 160–183쪽, 케임브리지 아리스토텔레스 탐험:케임브리지 대학교1996년 박사ISBN 0-521-55619-8.
  • 마하, 에른스트, The Science of Mechanics Open Court 1960.
  • 정확한 과학의 문턱에 있는 마이어, Annalise: 중세 후기 자연철학에 관한 Annalise Maier의 선집(필라델피아 스티븐 사겐트 편집):펜실베니아 대학 출판사, 1982년.
  • McCluskey, Stephen C., 초기 중세 유럽의 천문학과 문화, 캠브리지:케임브리지 대학교1998년 박사ISBN 0-521-77852-2
  • Neugebauer, Otto, 고대 수학 천문학사, 3권, 뉴욕: Springer, 1975.ISBN 0-387-06995-X
  • Pederson, Olaf (1993) [1974]. Early Physics and Astronomy: A Historical Introduction. Cambridge: Cambridge University Press. ISBN 978-0-521-40340-5.
  • 포퍼, 칼, 파르메니데스 루트리지 1996
  • 로젠, 에드워드, 코페르니쿠스 논문 3권 1939/59년
  • S. Sambursky, The Physical World of Late Antious Routledge & Kegan Paul, 1962년
  • 스코필드, C., Taton & Wilson의 Tychonic 및 Semi-Tychonic World Systems (eds) 1989
  • Sorabji, Richard, Matter, Space and Motion 런던:덕워스, 1988년 ISBN 0-7156-2205-6
  • 소라브지, 리처드, (ed.) 필로포노스와 아리스토텔레스 과학 런던과 이타카 NY 1987년
  • Sorabji, Richard, 해설자의 철학, 서기 200~600년: 제2권 물리 Duckworth
  • Taliaferro, R. Catesby (1946). Translator's Introduction to the Almagest. In Hutchins (1952, pp.1–4).
  • R. Taton & C.윌슨(에드), 천문학의 일반사: 제2권 르네상스부터 천체물리학 제A부 티코 브라헤에서 뉴턴 캠브리지까지:케임브리지 대학교1989년 박사
  • 토렌, 빅터 E., "1577년의 혜성과 티코 브라헤의 세계계" 국제사학사, 29(1979): 53~67.
  • Taton & Wilson 1989의 Tycho Brahe, Victor E.
  • Van Helden, Albert (1985). Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley. Chicago and London: University of Chicago Press. ISBN 978-0-226-84882-2.

외부 링크

Wikimedia Commons에는 천구(우주학적 모델)와 관련된 미디어가 있습니다.