투영직교군

투사 기하학 및 선형 대수학에서 투사 직교 그룹 PO는 관련 투사 공간 P(V)에서 2차 공간 V = (V,Q)^{[note 1]}의 직교 그룹의 유도 작용이다.명시적으로 투영직교 그룹은 지수 그룹이다.

PO(V) = O(V)/ZO(V) = O(V)/{±I}

여기서 O(V)는 (V)와 ZO(V)={±의 직교 그룹이다.I}은 V의 모든 직교 스칼라 변환의 부분군이며, 이들은 원점을 통한 정체성과 반사로 구성된다.이러한 스칼라들은 투사공간에 사소한 작용을 하고 작용의 커널을 형성하기 때문에 지수화되며, "Z"라는 표기법은 스칼라 변환이 직교군의 중심이기 때문이다.

투사 특수 직교 그룹 PSO는 관련 투사 공간에서 특수 직교 그룹의 유도 작용과 유사하게 정의된다.명시적으로:

PSO(V) = SO(V)/ZSO(V)

여기서 SO(V)는 V에 대한 특수 직교 그룹이고 ZSO(V)는 단위 결정 인자를 갖는 직교 스칼라 변환의 하위 그룹이다.여기서 ZSO는 SO의 중심이며 홀수 차원에서는 사소하지만 짝수 차원에서는 {±1}과 같다. 이러한 홀수/짝수 차이는 직교 그룹의 구조 전반에 걸쳐 발생한다.GL/SL, GO/SO와 유추하여 투사직교군(projective general orthogonal group)을 투사일반직교군(projective general orgonal group)이라고도 하며 PGO를 나타낸다.

직교 그룹과 마찬가지로, 투사 직교 그룹은 모든 분야에 걸쳐 정의될 수 있고 다양한 2차 형태로 정의될 수 있지만, 일반 직교 그룹과 마찬가지로, 주요 강조점은 실제 양의 확실한 투사 직교 그룹에 있다. 다른 분야는 아래에 일반화에 상세하게 설명되어 있다.달리 언급된 경우를 제외하고, 후속편에서 PO와 PSO는 진짜 긍정적인 확정 그룹을 언급할 것이다.

(특수)직교 그룹의 인용보다는 커버인 스핀 그룹과 핀 그룹처럼, 투사(특수)직교 그룹은 유클리드 기하학의 (투사) 기하학적 아날로그, 관련 리 그룹 및 표현 이론에 관심이 있다.

보다 본질적으로 (실제 양정확정) 투사 직교 그룹 PO는 타원 공간의 등위계(타원 기하학의 의미)로 정의될 수 있는 반면, PSO는 타원 공간의 방향 보존 등위계(공간이 방향성이 있는 경우, 그렇지 않은 경우 PSO = PO)로 정의할 수 있다.

구조

홀수 및 짝수 치수

The structure of PO differs significantly between odd and even dimension, fundamentally because in even dimension, reflection through the origin is orientation-preserving, while in odd dimension it is orientation-reversing ( $-I\in \operatorname {SO} (2k)$ but ${\displaystyle -I\no$ $t \in \operatorname {SO}(2k+1)$ ). $-I\not \in \operatorname {SO} (2k+1)$ 이는 각 홀수차원 실제 투영 공간은 방향성이 있는 반면, 양차원의 각 짝수차원 실제 투영 공간은 방향성이 없다는 점에서 볼 수 있다.좀 더 추상적인 수준에서 홀수 및 짝수차원 투영직교 그룹의 리알헤브라는 두 개의 다른 패밀리를 형성한다: $B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.$ k $B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.$ = $B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.$ $B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.$ $B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.$ + $B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.$ , $B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.$ = $B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.$ . $B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.$ $B_{k}={\mathfrak {so}}_{2k+1},D_{k}={\mathfrak {so}}_{2k}.$ ${\displaystyle B_{k}={2k+1},D_{k}={mathfrak{so}}_{}}}}.$ $}$

Thus, $O(2k+1)=\operatorname {SO} (2k+1)\times \{\pm I\},$ ^{[note 2]} while $O(2k)\neq \operatorname {SO} (2k)\times \{\pm I\}$ and is instead a non-trivial central extension of PO(2k).

Beware that PO(2k+1) is isometries of $\mathbf {RP} ^{2k}=\mathbf {P} (\mathbf {R} ^{2k+1}),$ while PO(2k) is isometries of $\mathbf {RP} ^{2k-1}=\mathbf {P} (\mathbf {R} ^{2k})$ – the odd-dimensional (vector) group is isome짝수차원의 투사공간을 시도하는 반면, 짝수차원의 집단은 홀수차원의 투사공간을 등분한다.

In odd dimension, $\operatorname {SO} (2k+1)\cong \operatorname {PSO} (2k+1)=\operatorname {PO} (2k+1),$ ^{[note 3]} so the group of projective isometries can be identified with the group of rotational isometries.

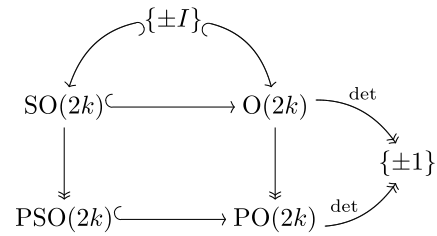
짝수치수에서 SO(2k)→PSO(2k)→O(2k)→PO(2k)는 모두 2대 1 커버, PSO(2k) <PO(2k)는 지수 2 서브그룹이다.

일반 속성

PSL과 PGL과 마찬가지로 PSO와 PO는 중심이 없다. 이는 스칼라 매트릭스가 SO와 O의 중심일 뿐만 아니라 하이퍼센터(중앙에 의한 양이 항상 중심이 없는 그룹을 산출하는 것은 아님)이기 때문이다.

PSO는 투사형 특수 선형 그룹 PSL에서 최대 콤팩트 부분군이고, PO는 투사형 일반 선형 그룹 PGL에서 최대 콤팩트다.이는 SL에서는 SO가 최대 소형이고 GL에서는 O가 최대 소형인 것과 유사하다.

표현 이론

PO는 표현 이론에 기본적 관심사: 집단 동형성 G → PGL은 지도 G → GL의 선형 표현이라 불리며, 어떤 선형 표현도 지도 G → O → (불변형 내부 제품을 취함으로써) 지도 G → O로 축소할 수 있는 것처럼, 어떠한 투영적 표현도 지도 G → 지도 G → PGL로 축소할 수 있다.PO.

자세한 내용은 투영 선형 그룹: 표현 이론을 참조하십시오.

부분군

투사 직교 그룹의 하위 그룹은 - $-I$ ${\displaystyle -I}($ 중앙 대칭)을 포함하는 직교 그룹의 하위 그룹에 해당한다.항상 지수(격자 정리) 지도가 있는 것처럼 O와 PO의 부분군 사이에는 갈루아 연결이 있는데, 여기에 O에 대한 결합(PO에서 이미지를 찍은 다음 O에서 프리이미지를 찍은 후 제공 $-I$ 이 없는 경우 $-I$ $-I$ - I {\ $displaystyle -I}$ 를 추가한다.

특히 관심사는 이산형 부분군이며, 이는 투사형 폴리탑의 대칭으로 실현될 수 있다 – 이것들은 중심 대칭을 포함하는 (분리형) 점 그룹에 해당한다.스핀 그룹의 이산 하위 그룹, 특히 이항 다면 그룹의 3차원 사례와 비교해 보십시오.

예를 들어, 3차원에서 5개의 플라톤 고형물 중 4개는 중심 대칭(큐브/옥타헤드론, 도데카헤드론/icosaheadron)을 가지지만, 4차면체는 그렇지 않지만, 결과 대칭 그룹은 입방체/옥타헤드론과 동일하다.

위상

PO와 PSO는 중심이 없는 위상학 그룹으로서 커버 그룹의 맨 아래에 있으며, 상단 그룹은 각각 (간단하게 연결된) 핀 그룹 또는 스핀 그룹이다.

핀_±(n) → O(n) → PO(n).

스핀(n) → SO(n) → PSO(n).

이 그룹들은 모두 같은 리 대수학의 작은 실제 형태들이다.

1대1(이형성)인 SO(2k+1)→PSO(2k+1)를 제외한 모든 2대1 커버다.

호모토피군

$\pi _{1}$ ${\$ } 이상의 호모토피 그룹은 커버 아래에서 변경되지 않으므로 $\pi _{1}$ 직교 그룹의 그룹과 일치한다.하부 호모토피 그룹은 다음과 같이 주어진다.

\pi _{0}(\operatorname {PSO})\cong 1

\pi _{0}{big (}\\operatorname {PO}(2k){\big )}\cong \mathbf {Z} /2,\pi _{0}{0}\big(}\\\\operatorname {PO}(2k+1){\big}\cong 1.

(중앙이 없는) PSO(n)의 기본 그룹은 (단순하게 연결된) 스핀(n)의 중심과 동일하며, 그룹을 다루는 것에 대해서는 항상 진실이다.

\pi _{1}{big(}\!\operatorname {PSO})(n)}=\pi _{1}{big(}\\\\operatorname {PO})(n)=Z{big(}\\\\\operatorname {Spin}{big)}.

스핀 그룹 중앙 표 사용( $k\geq 1$ $k\geq 1$ 1 ${\displaystyle k\geq$ 1 $}$ 의 경우): $k\geq 1$

\pi _{1}{big (}\!\operatorname {PSO}{\big )}=\mathbf {Z} /2\oplus \mathbf {Z} /2,

\pi _{1}{{1}{{1}\big!\operatorname {PSO}(4k+2){\big )=\mathbf {Z} /4,

\pi _{1}{big(}\!\operatorname {PSO}(2k+1){big(}\big)}=\pi _{1}{big(}\\\operatorname {SO}{k+1){big)=\mathbf {Z}/2,},

저차원의 경우:

\pi _{1}{\big (}\!\operatorname {PSO} (1){\big )}=1,

\pi _{1}{\big (}\!\operatorname {PSO} (1){\big )}=1,

(

\pi _{1}{\big (}\!\operatorname {PSO} (1){\big )}=1,

\pi _{1}{\big (}\!\operatorname {PSO} (1){\big )}=1,

(

\pi _{1}{\big (}\!\operatorname {PSO} (1){\big )}=1,

1

\pi _{1}{\big (}\!\operatorname {PSO} (1){\big )}=1,

)

\pi _{1}{\big (}\!\operatorname {PSO} (1){\big )}=1,

= 1

\pi _{1}{\big (}\!\operatorname {PSO} (1){\big )}=1,

,

{\displaystyle \pi _{1}{

1}{

big (}\\\operatorname {PSO}(1){\big )}=1,}

그룹은 사소한 것이므로

\pi _{1}{\big (}\!\operatorname {PSO} (1){\big )}=1,

.

\pi _{1}{\big (}\!\operatorname {PSO} (2){\big )}=\mathbf {Z} ,

as it is topologically a circle, though note that the preimage of the identity in Spin(2) is

\mathbf {Z} /4,

as for other

{\displaystyle 4k+2.

}

호몰로지 집단

번들

직교 그룹이 벡터 번들의 구조 그룹인 것처럼, 투사 직교 그룹은 투사 번들의 구조 그룹이며, 해당 분류 공간은 BPO로 표시된다.

일반화

직교 그룹과 마찬가지로 투사 직교 그룹은 두 가지 주요 방법으로 일반화할 수 있다: 필드 변경 또는 2차 형태 변경.실수 이외의 1차적 관심사는 복잡한 수나 유한한 분야에 있으며, (실제 상공에서) 2차적 형태도 무기한 형식이 될 수 있으며, 그 서명으로 PO(p,q)로 표기된다.

복잡한투사 직교 그룹인 PO(n,C)를 투사적 단일 그룹인 PU(n)와 혼동해서는안 된다. PO는 대칭형태를 보존하는 반면, PU는 은둔적형태를 보존한다 – PU는 복합 투사적공간의 대칭이다(푸비니-스터디 메트릭 보존).

특성 2의 분야에는 2차 형태와 대칭 이선형 형태가 더 이상 동등하지 않으며 $I=-I,$ , $I=-I,$ = - $I=-I,$ , ${\displaystyle I=-I,},$ 결정인자를 딕슨 불변성으로 교체해야 한다.

유한장

유한분야에 걸친 투영직교그룹은 Lie형의 유한단순군, 즉 D형의_n Chevalley 군을 구성하는 데 사용된다.유한분야에 걸친 직교군 O(n,q)는 부분군으로서 SO를, 비종교 중심({±I})을 가지고 있기 때문에 단순하지 않다.이 두 가지 모두 PSO에 전달함으로써 고정되지만 PSO 자체는 일반적으로 단순하지 않으며, 그 대신 스피너 규범(이상한 특성)이나 준위계(짝수 특성)에 의해 정의된 부분군(지수 1 또는 2일 수 있음)을 사용해야 한다.^[1]quasideterminant는 $(-1)^{D}$ ( $(-1)^{D}$ - $(-1)^{D}$ ) $(-1)^{D}$ ${\$ 로 정의할 수 있으며, 여기서 $(-1)^{D}$ D는 딕슨 불변제(Dickson 불변제에 의해 정의된 결정인자) 또는 고정 공간의 치수에 관해서도 정의될 수 있다.

메모들

^ 2차 공간은 2차 형태 Q와 함께 벡터 공간 V로, Q는 명확할 때 표기법에서 삭제된다.
^ 이 제품은 추상적인 외부 직접 합이 아니라 내부 직접 합(부분군 제품)이다.
^ 이 방정식의 이형성/평등성 구별은 컨텍스트가 2 대 1의 지수 $O\to \operatorname {PO}$ O $O\to \operatorname {PO}$ → $O\to \operatorname {PO}$ $O\to \operatorname {PO$ \to \operatorname} – \operatorname{PSO}(2k+1) 및 \operatorname{{PO}(2k+1)은 대상(명칭, 전체 공간)의 동일한 하위 집합이므로 동등하며, 유도 맵 $\operatorname {SO} \to \operatorname {PSO}$ → $\operatorname {SO} \to \operatorname {PSO}$ $\operatorname {SO} \to \operatorname {PSO}$ 은 $\operatorname {SO} \to \operatorname {PSO}$ (는) 이형이지만 두 그룹은 서로 다른 공간의 하위 집합이므로 동등성이 아니라 이형이다.이러한 구분이 이루어지는 예는 (Conway & Smith 2003, 페이지 34)를 참조하십시오.

참고 항목

참조

^ ATLAS, 페이지 xi

Conway, John Horton; Smith, Derek Alan (2003-02-07), "3.7 The Projective or Elliptic Groups", On quaternions and octonions, A K Peters, Ltd., pp. 34, ISBN 978-1-56881-134-5
Conway, J. H.; Curtis, R. T.; Norton, S. P.; Parker, R. A.; and Wilson, R. A. "The Groups GO_n(q), SO_n(q), PGO_n(q), and PSO_n(q), and O_n(q)." §2.4 in Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups.영국 옥스포드: Clarendon Press, pp. xi–xii, 1985.

외부 링크

[1] 2차 공간은 2차 형태 Q와 함께 벡터 공간 V로, Q는 명확할 때 표기법에서 삭제된다.

[2] 이 제품은 추상적인 외부 직접 합이 아니라 내부 직접 합(부분군 제품)이다.

[3] 이 방정식의 이형성/평등성 구별은 컨텍스트가 2 대 1의 지수 $O\to \operatorname {PO}$ O $O\to \operatorname {PO}$ → $O\to \operatorname {PO}$ $O\to \operatorname {PO$ \to \operatorname} – \operatorname{PSO}(2k+1) 및 \operatorname{{PO}(2k+1)은 대상(명칭, 전체 공간)의 동일한 하위 집합이므로 동등하며, 유도 맵 $\operatorname {SO} \to \operatorname {PSO}$ → $\operatorname {SO} \to \operatorname {PSO}$ $\operatorname {SO} \to \operatorname {PSO}$ 은 $\operatorname {SO} \to \operatorname {PSO}$ (는) 이형이지만 두 그룹은 서로 다른 공간의 하위 집합이므로 동등성이 아니라 이형이다.이러한 구분이 이루어지는 예는 (Conway & Smith 2003, 페이지 34)를 참조하십시오.

[4] ATLAS, 페이지 xi

[note 1]

[note 2]

[note 3]

[1]

Search