사분위수나 사분위수와 혼동해서는안 된다.
도 2의 다항식 0의 위치
수학에서 사분면 또는 사분면 (높은 치수 의 사분면 )은 원뿔면 (엘립스 , 파라볼라 , 하이퍼볼라 )의 일반화 다. a(D + 1)차원 공간에 있는 (D 치수 D의) 과외면 이며, D + 1 변수에서 2도(원뿔 부분 경우 D = 1)의 무적화 다항식 0 집합 으로 정의된다. 정의 다항식이 절대적으로 해석 할 수 없는 경우, 퇴행형 사분면 또는 환원형 사분면 이라고 하는 경우가 많지만, 일반적으로 0 집합은 사분면으로 간주되지 않는다.
좌표 x 1 ,x 2 , ...,x D +1대수 방정식 으로[1]
∑ i , j = 1 D + 1 x i Q i j x j + ∑ i = 1 D + 1 P i x i + R = 0 {\displaystyle \sum _{i,j=1}^{D+1}x_{d+1}Q_{ij}x_{j}+\sum _{i=1}{d+1}P_{i}x_{i}+R=0} 벡터 및 행렬 표기로 다음과 같이 압축적으로 작성할 수 있다.
x Q x T + P x T + R = 0 {\displaystyle xQx^{\mathrm {T}+Px^{\mathrm {T}}+R=0\,} 여기서 x =x1 2 , ..., x) 는D +1벡터 , x 는T x(열 벡터)의 전치 , Q 는 (D + 1)× (D ) 행렬 , P 는 (D + 1R 은 스칼라 상수다. Q , P , R 값은 종종 실수 나 복잡한 숫자 에 대해 취해지지만, 어떤 분야 에서도 사분위가 정의될 수 있다.
사분위는 아핀 대수적 품종 , 또는 환원 가능한 경우 아핀 대수적 집합 이다. 사분위는 투영 공간 에서도 정의될 수 있다. 아래의 § 투영 기하학 을 참조한다.
유클리드 평면 유클리드 평면 의 치수는 2이므로 유클리드 평면의 사분위는 1 치수를 가지므로 평면 곡선 이 된다. 그것들은 원추형 또는 원추형 이라고 불린다.
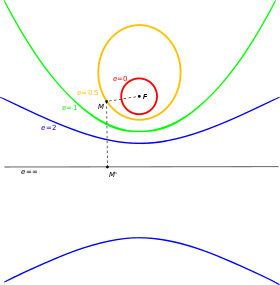
고정 초점 F 와 다이렉트릭스가 있는 원(e = 0), 타원(e = 0.5), 파라볼라(e = 1) 및 하이퍼볼라(e = 2) 유클리드 공간 3차원 유클리드 공간 에서 사분면은 차원 D = 2를 가지며, 사분면 이라고 알려져 있다. 그것들은 부착된 변형 하에서 궤도 로 분류되고 이름이 지어진다. 더 정확히 말하면, 만약 아핀 변환이 4중치를 다른 것에 매핑한다면, 그들은 같은 등급에 속하며, 같은 이름과 많은 속성을 공유한다.
주축 정리 는 모든 (감소 가능한) 사분면에 대해 적절한 유클리드 변환 또는 데카르트 좌표 변경을 통해 사분면의 2차 방정식을 다음과 같은 정상적인 형태 중 하나에 넣을 수 있음을 보여준다.
x 2 a 2 + y 2 b 2 + ε 1 z 2 c 2 + ε 2 = 0 , {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+\varepsilon _{1}{z^{2} \over c^{2}}+\barepsilon _{2} \2}=0,} x 2 a 2 − y 2 b 2 + ε 3 = 0 {\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}+\varepsilon _{3}=0} x 2 a 2 + ε 4 = 0 , {\displaystyle {x^{2} \over a^{2}}+\varepsilon _{4}=0,} z = x 2 a 2 + ε 5 y 2 b 2 , {\displaystyle z={x^{2} \over a^{2}}+\varepsilon_{5}{y^{2} \over b^{2}},} 여기서 ε i {\ displaystyle \varepsilon _ {i} 3 {\ displaystyle \varepsilon 3}
이 17개의 정상 형태는[2] In three cases there are no real points: ε 1 = ε 2 = 1 {\displaystyle \varepsilon _{1}=\varepsilon _{2}=1} imaginary ellipsoid ), ε 1 = 0 , ε 2 = 1 {\displaystyle \varepsilon _{1}=0,\varepsilon _{2}=1} imaginary elliptic cylinder ), and ε 4 = 1 {\displaystyle \varepsilon _{4}=1} complex conjugat e 병렬 평면, 축소 가능한 사분면). 하나 의 경우, 가상의 원뿔 에는 하나의 점이 있다(ε1 2 0 displaystyle \varepsilon _{1}=1,\varepsilon _{2}=0}). ε 1 ε 2 0 , {\displaystyle \varepsilon _{1}=\varepsilon _{ 0,} ε 3 0 , {\displaystyle \var렙실론 _{3}=0,} ε 4 0 , {\displaystyle \varepsilon _{4}=0,} ε 4 1 {\displaystyle \varepsilon _{4}=-1,}
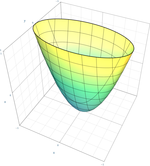
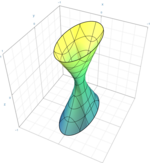
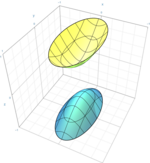
따라서 17개의 정상적인 형태 중 9개의 진정한 사분위가 있는데, 원추형, 3개의 원통형(흔히 퇴행형 사분체라고 불림)과 5개의 비퇴행형 사분체(엘립소이드 , 파라볼로이드 , 하이퍼볼로이드 )가 다음 표에 자세히 설명되어 있다. 나머지 8개의 사분위는 상상의 타원체(실제점 없음), 상상의 원통(실제점 없음), 상상의 원뿔(실제점 없음), 환원 가능한 사분위(단일 실점), 두 개의 평면으로 분해된다; 평면의 구별 여부에 따라 그러한 분해된 사분위가 5개 있다. 대문을 열다
표준 방정식의 매개변수 중 두 개 이상이 같을 때, 한 축(또는 구의 경우 무한히 많은 축)을 회전할 때 불변으로 남아 있는 4분의 1의 혁명 을 얻는다.
정의 및 기본 속성 아핀 사분위 는 도 2의 다항식의 0 의 집합이다. 달리 명시되지 않은 경우, 다항식은 실제 계수를 가지도록 되어 있으며, 0은 유클리드 공간 에 있는 점들이다. 그러나 대부분의 특성은 계수가 어떤 필드 에 속하고 점이 부속 공간 에 속할 때 참으로 남아 있다. 대수 기하학 에서 보통 그렇듯이, 계수가 실제일 때 다항식 계수, 일반적으로 복합수 를 포함하는 대수적으로 닫힌 장 에 대한 점을 고려하는 것이 종종 유용하다.
많은 성질은 무한대에 점 을 추가하는 것으로 구성되는 투영완성 에 의해 사분면을 투영공간 으로 확장함으로써 진술하기 쉬워진다(그리고 증명하기 쉽다). 엄밀히 말하면
p ( x 1 , … , x n ) {\displaystyle p(x_{1},\ldots ,x_{n}}} 아핀 사분면을 정의하는 2급 다항식이다. 그러면 그 투영적 완성은 p 를 로 균질화함 으로써 정의된다.
P ( X 0 , … , X n ) = X 0 2 p ( X 1 X 0 , … , X n X 0 ) {\displaystyle P(X_{0},\ldots,X_{n}}=X_{0}^{2}\,p\좌({\frac{X_{1}{0}}},\ldots,{\frac {X_{n}}}},{X_{0}}}\rig)}}} (p 의 정도가 2이기 때문에 이것은 다항식이다.) 투사 완료 지점은 투사 좌표 가 P 의 0인 투사 공간의 점이다.
따라서, 투영 사분면 은 2도의 동종 다항식 의 투영 공간에 있는 0의 집합이다.
위의 동질화 과정은 X 0 설정 하여 되돌릴 수 있기 때문이다.
p ( x 1 , … , x n ) = P ( 1 , x 1 , … , x n ) , {\displaystyle p(x_{1},\ldots,x_{n}}=P(1,x_{1},\ldots,x_{n}\}). 아핀 4중방과 그것의 투영적인 완성을 구분하지 않는 것이 종종 유용하며, 아핀 방정식 또는 4중방의 투영 방정식 을 말하는 것이 유용하다. However, this is not a perfect equivalence; it is generally the case that P ( X ) = 0 {\displaystyle P(\mathbf {X} )=0} X 0 = 0 {\displaystyle X_{0}=0} p ( x ) = 0 {\displaystyle p(\mathbf {x} )=0} s 부속 공간의 "무한도"에서.
방정식 치수 n 의 부속 공간 에 있는 사분위는 도 2의 다항식 0의 집합이다. 즉, 좌표가 방정식을 만족하는 점들의 집합이다.
p ( x 1 , … , x n ) = 0 , {\displaystyle p(x_{1},\ldots,x_{n}=0,} 다항식 p 가 형태를 갖는 곳
p ( x 1 , … , x n ) = ∑ i = 1 n ∑ j = 1 n a i , j x i x j + ∑ i = 1 n ( a i , 0 + a 0 , i ) x i + a 0 , 0 , {\displaystyle p(x_{1},\ldots ,x_{n})=\sum _{i=1}^{n}\sum _{j=1}^{n}a_{i,j}x_{i}x_{j}+\sum _{i=1}^{n}(a_{i,0}+a_{0,i})x_{i}+a_{0,0}\,,} for a matrix A = ( a i , j ) {\displaystyle A=(a_{i,j})} i {\displaystyle i} j {\displaystyle j} n {\displaystyle n} characteristic of the field of the coefficients is not two, generally a i , j = a j , i {\displaystyle a_{i,j}=a_{j,i}} ly A A T {\ displaystyle A=A^{\mathsf{T a j 0 {\displaystyle a_{i,j}=0} ( 가 < i {\displaysty j< } 동등 displaystystystystysty 삼각형 일
행렬 방정식으로 방정식을 단축할 수 있다.
x T A x = 0 , {\displaystyle \mathbf {x} ^{\mathsf {T}A\mathbf {x} =0\...} 와 함께
x = ( 1 x 1 ⋯ x n ) T . {\displaystyle \mathbf {x} ={\begin{pmatrix}1&x_{1}\cdots &x_{n}\end{pmatrix}}^{\mathsf {T}\,.} 투영완성의 방정식은 거의 동일하다.
X T A X = 0 , {\displaystyle \mathbf {X} ^{\mathsf {T}A\mathbf {X} =0,} 와 함께
X = ( X 0 X 1 ⋯ X n ) T . {\displaystyle \mathbf {X} ={\begin{pmatrix}X_{0}&X_{1}&\cdots &X_{n}\end{pmatrix}}^{\mathsf {T}}}. } 이러한 방정식은 차원 n의 공간 에서 차원 n – 1 과 도 2의 대수적 초대면 으로서 사분면을 정의한다.
매트릭스 A {\displaystyle A} 불가능 한 경우 사분위는 소멸 되지 않는다고 한다.
투영 사분면의 정상 형태 실베스터의 관성 법칙 에 의해 실제 투사 공간 에서는 비성 2차 형태 P (X )를 정상 형태로 넣을 수 있다.
P ( X ) = ± X 0 2 ± X 1 2 ± ⋯ ± X D + 1 2 {\displaystyle P(X)=\pm X_{0}^{2}\pm X_{1}^{1}^{2}\pm \cdots \pm X_{D+1}^{2} }} 적절한 투영적 변환 을 통해(단수 사분위에 대한 정규 형태는 계수로 ±1과 0을 가질 수 있다. 3차원 공간의 2차원 표면(차원 D = 2)의 경우, 정확하게 세 가지 비감속 사례가 있다.
P ( X ) = { X 0 2 + X 1 2 + X 2 2 + X 3 2 X 0 2 + X 1 2 + X 2 2 − X 3 2 X 0 2 + X 1 2 − X 2 2 − X 3 2 {\displaystyle P(X)={\begin}X_{0}^{2}+X_{1}^{1}^{2}+X_{2}^{2}+X_{3} }^{2}\\X_{0}^{2}+X_{1}^{2}+X_{2}^{2}-X_{3}^{2}\\X_{0}^{2}+X_{1}^{2}-X_{2}^{2}-X_{3}^{2}\end{cases}}} 첫 번째 경우는 빈 세트다.
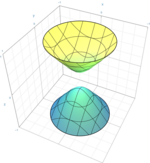
두 번째 경우는 무한대의 선택된 평면이 빈 세트, 점 또는 비감산 원뿔에서 각각 사분면을 절단하는지에 따라 타원체, 타원형 파라볼로이드 또는 두 장의 하이퍼볼로이드를 생성한다. 이것들은 모두 양의 가우스 곡률 을 가지고 있다.
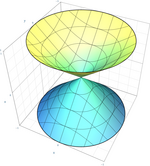
세 번째 경우는 무한대의 평면이 각각 두 개의 선으로 자르는지, 또는 비생성 원뿔체로 자르는지에 따라 쌍곡선 포물선 또는 한 장의 하이퍼볼로이드를 생성한다. 이것들은 음의 가우스 곡률의 이중 지배 표면 이다.
타락한 형태
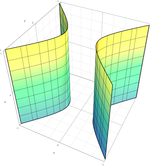
X 0 2 − X 1 2 − X 2 2 = 0. {\displaystyle X_{0}^{2}-X_{1}^{2}-X_{2}^{2}=0.\,} 무한대의 평면이 점, 선, 두 선 또는 비감발 원뿔에서 각각 절단하는지에 따라 타원형 실린더, 포물선 실린더, 쌍곡선 실린더 또는 원뿔을 생성한다. 이것들은 가우스 곡률 제로 단독 지배 표면이다.
우리는 투영적 변환이 가우스 곡선 형태의 다른 부호를 섞지 않는다는 것을 안다. 이것은 일반적인 표면에 적용된다.[3]
복잡한 투영 공간 에서 모든 비감소 사분위는 서로 구별할 수 없게 된다.
정수 및 합리적인 솔루션 Each solution of p ( x ) = 0 {\displaystyle p(\mathbf {x} )=0} x {\displaystyle \mathbf {x} } X ≠ 0 {\displaystyle \mathbf {X} \neq \mathbf {0} } P ( X ) = 0 {\displaystyle P(\mathbf {X} )=0} X = k ( 1 , x {\displaystyle \ mathbf {X} =k(1,\mathbf {x} k {\displaystyle k} x {\ displaystyle mathbf {x} .
또한, 기본 행렬이 변위할 수 없는 경우, 합리적 인 구성요소가 있는{\ displaystyle \mathbf {y} 대한 y 0 {\displaystyle p(\mathbf {y} )=0} Let X = Y + λ Z {\displaystyle \mathbf {X} =\mathbf {Y} +\lambda \mathbf {Z} } Y ≠ 0 {\displaystyle \mathbf {Y} \neq \mathbf {0} } Z ≠ 0 {\displaystyle \mathbf {Z} \neq \mathbf {0} } λ {\displaystyle \lambda } P ( X ) = X X {\ displaystyle P(\mathbf {X} )=\mathbf {X} ^{\mathsf {T}A\mathbf {X}} 행렬 displaystyle
P ( X ) = Y T A Y + 2 λ Y T A Z + λ 2 Z T A Z . {\displaystyle P(\mathbf {X} )=\mathbf {Y} ^{\mathsf {T}}A\mathbf {Y} +2\lambda \mathbf {Y} ^{\mathsf {T}}A\mathbf {Z} +\lambda ^{2}\mathbf {Z} ^{\mathsf {T}}A\mathbf {Z} \,.} 언제
Y T A Y = 0 , Y T A Z ≠ 0 , Z T A Z ≠ 0 {\displaystyle {\begin{aligned}\mathbf {Y} ^{\mathsf {T}}A\mathbf {Y} &=0,\\\mathbf {Y} ^{\mathsf {T}}A\mathbf {Z} &\neq 0,\\\mathbf {Z} ^{\mathsf {T}}A\mathbf {Z} &\neq 0\end{aligned}}} then the two solutions to P ( X ) = 0 {\displaystyle P(\mathbf {X} )=0} λ {\displaystyle \lambda } λ = 0 , − ( 2 Y T A Z ) / ( Z T A Z ) {\displaystyle \lambda =0,-(2\mathbf {Y} ^{\mathsf {T}}A\mathbf {Z} )/(\mathbf {Z} ^{\mathsf {T}}A\mathbf {Z} )} 후자는 0이 아니고 합리적이다. In particular, if y {\displaystyle \mathbf {y} } p ( y ) = 0 {\displaystyle p(\mathbf {y} )=0} Y {\displaystyle \mathbf {Y} } P ( Y ) = 0 {\displaystyle P(\mathbf {Y} )=0} Z {\displaystyle \mathbf {Z} } Z {\displaystyle \mathbf {Z} } A Y {\displaystyle A\mathbf {Y} } Z T A Z ≠ 0 {\displaystyle \mathbf {Z} ^{\mathsf {T}}A\mathbf {Z} \neq 0} λ {\displaystyle \lambda }
In short, if one knows one solution y {\displaystyle \mathbf {y} } W Z = ( Z T A Z ) Y − ( 2 Y T A Z ) Z {\displaystyle \mathbf {W} _{\mathbf {Z} }=(\mathbf {Z} ^{\mathsf {T}}A\mathbf {Z} )\mathbf {Y} -(2\mathbf {Y} ^{\mathsf {T}}A\math bf {Z} )\mathbf {Z} W Z {\ displaystyle \ mathbf {W} _{\ mathbf {Z}}} 선택 . If both y {\displaystyle \mathbf {y} } p ( y ) = 0 {\displaystyle p(\mathbf {y} )=0} w {\displaystyle \mathbf {w} } p ( w ) = 0 {\displaystyle p(\mathbf {w} )=0} Z = W − Y {\displaystyle \mathbf {Z} =\mathbf {W} -\mathbf {Y} } W Z W {\ displaystyle \mathbf {W} _{\mathbf {Z} }=\mathbf {W 피타고라스의 3배 또는 헤로니아 삼각형 을 모두 생성할 수 있다.
필드 위에 투영 사분위수 실제 투사 공간에서 투사 사분면의 정의(위 참조)는 필드 위에 있는 n차원 투사 공간에서 투사 사분면을 정의하는 것을 공식적으로 채택할 수 있다. 좌표 처리를 생략하기 위해 일반적으로 투영적 사분위는 벡터 공간에 2차 형태로 정의된다.
이차형 K {\displaystyle K} 필드 로 하고 {\displaystyle V } 벡터 공간 으로 K {\displaystyle K} . {\displaystyle V} K {\displaysty } q {\ q}
(Q1) q ( λ x → ) = λ 2 q ( x → ) {\displaystyle \;q(\lambda {\vec {x}})=\lambda ^{2}q({\vec {x}})\;} λ ∈ K {\displaystyle \lambda \in K} x → ∈ V {\displaystyle {\vec {x}}\in V} (Q2) f ( x → , y → ) := q ( x → + y → ) − q ( x → ) − q ( y → ) {\displaystyle \;f({\vec {x}},{\vec {y}}):=q({\vec {x}}+{\vec {y}})-q({\vec {x}})-q({\vec {y}})\;} bilinear form .2차 형태 이선형 {\displaystyle f} .
In case of char K ≠ 2 {\displaystyle \operatorname {char} K\neq 2} f ( x → , x → ) = 2 q ( x → ) {\displaystyle f({\vec {x}},{\vec {x}})=2q({\vec {x}})} f {\displaystyle f} q {\displaystyle q} In case of char K = 2 {\displaystyle \operatorname {char} K=2} 1 + 1 = 0 {\displaystyle 1+1=0} f ( x → , x → ) = 0 {\displaystyle f({\vec {x}},{\vec {x}})=0} f {\displaystyle f} symplectic
For V = K n {\displaystyle V=K^{n}\ } x → = ∑ i = 1 n x i e → i {\displaystyle \ {\vec {x}}=\sum _{i=1}^{n}x_{i}{\vec {e}}_{i}\quad } { e → 1 , … , e → n } {\displaystyle \{{\vec {e}}_{1},\ldots ,{\vec {e}}_{n}\}} V {\displaystyle V} q \displaystyle q}
q ( x → ) = ∑ 1 = i ≤ k n a i k x i x k with a i k := f ( e → i , e → k ) for i ≠ k and a i i := q ( e → i ) {\displaystyle q({\vec {x}})=\sum _{1=i\leq k}^{n}a_{ik}x_{i}x_{k}\ {\text{ with }}\ a_{ik}:=f({\vec {e}}_{i},{\vec {e}}_{k})\ {\text{ for }}\ i\ne q\ {\text{ }\ a_{ii}:=q({\vec{e}_ {i}\} f x y ∑ 1 i ≤ a k x k k y i displaystyle ({\vec{x},{\vec {y}}=\sum _{1=i \leq }^{na}a_{k_{k}x_{k}y_ { k}. 예를 들면 다음과 같다.
n = 3 , q ( x → ) = x 1 x 2 − x 3 2 , f ( x → , y → ) = x 1 y 2 + x 2 y 1 − 2 x 3 y 3 . {\displaystyle n=3,\displaystyle q({\vec {x}=x_{1}x_{2}-{3}^{2},\bec {y}}}}=x_{1}y_{1}{1}y_{1}-{3x_{3}.};}. 들판 위의 n차원 투사 공간 K {\displaystyle K} 2 ∈ N {\ displaystyle 2\leq \in \mathb {N
필드 K {\displaystyle K,} 1 {\ displaystyle V_{n+1} 1 )차원 벡터 공간 ⟨ x \{\displaystyle \langle{\vec}\ langle } 0 → ≠ x V 1 {\ vec 스타일 {\0}\nec{\bec}\in V_{n+1 P ⟨ ∣ v n 1 }, {\ displaystyle {\mathcal{P}=\\\langle {\\bec{x}}\rangele \mid {\\bec}\{n+1}\}} 포인트 집합 , G n 1 } 2차원 서브스페이스 {\displaystyle {G}=\{\\text{n2차원 서브스페이스 } V_ {n+1}\} P n K G {\ displaystyle P_{n}(K)=({\mathcal{P},{\mathcal{G})\}\}}} K displaystyle K} 투영 . V n 1 k (k+1)} 1 {\ displaystyle V_{n+1} P displaystyle P_{n}(K)} displaystystystyle k} 아공간 이다. n 3 {\ displaystyle \;n]3\;} n 1 {\displaystyle (n-1) 하이퍼플레인 이라고 한다.투영 사분면체 For a quadratic form q {\displaystyle q} V n + 1 {\displaystyle V_{n+1}} ⟨ x → ⟩ ∈ P {\displaystyle \langle {\vec {x}}\rangle \in {\mathcal {P}}} singular if q ( x → ) = 0 {\displaystyle q({\vec {x}})=0}
Q = { ⟨ x → ⟩ ∈ P ∣ q ( x → ) = 0 } {\displaystyle {\mathcal {{Q}=\\langle {\vec}\x}\angle \in {\mathcal {P}\mid q({\vec {x}})=0\}}} Q {\displaystyle q} 4중 이라고 한다(이중q {\displaystyle q}
P 2 K {\displaystyle P_{2}(K)} (E1): q ( x → 1 x 2 x 3 displaystyle q({\vec{x}}}=x_{ x_{2}-x_{3}^{2}\} 원뿔 을 얻는다( E2 q( 1 x 2 {\ displaystyle \;q({\vec{x}})=x_{1}x_{2}\;} 1 0 {\displaystyle x_{1}= 0 }, x {\displaystystyle x_{2}=0}, 그들은 ⟨ ( 0 , , 1 T ⟩ {\displaystyle \langle (0,0,1)^{\text{ T}\rangele }
아래 고려사항에 대해서는 Q ≠ ∅ {\displaystyle {\mathcal {Q}\neq \emptyset } .
극공간 포인트 P ⟨ p ⟩ P {\ displaystyle P=\langle {\vec}\rangle \in mathcal {P}}
P ⊥ := { ⟨ x → ⟩ ∈ P ∣ f ( p → , x → ) = 0 } {\displaystyle P^{\perp }=\{\langle {\vec}}\angle \in {\mathcal {P}\mid f({\vec {p},{\vec}}}}=0\}}}}}}} P {\displaystyle P} 극공간 q}
f ( p x {\ displaystyle \;f({\vec{p}},{\vec{x}}}=0\;}, 임의 displaystyle{\vec{x 대해 ⊥ P {\ displaystystyle P^{\p={P}}}}}} .
If f ( p → , x → ) ≠ 0 {\displaystyle \;f({\vec {p}},{\vec {x}})\neq 0\;} x → {\displaystyle {\vec {x}}} f ( p → , x → ) = 0 {\displaystyle \;f({\vec {p}},{\vec {x}})=0\;} 그러므로
P ⊥{\ displaystyle P^{\perp }}} 하이퍼플레인 또는 P {\ displaystyle {\mathcal {P}} . 선과 교차점 4중 Q {\ displaystyle {\mathcal{Q}}
임의 라인 g {\displaystyle g} a) g ∩ Q ∅ {\ displaystyle g\cap {\mathcal{Q}=\emptyset \;}, {\displaystyle g} 외부 라인 또는 b) g ⊂ Q {\ displaystyle g\subset {\mathcal {Q}\;} {\displaystyle g} 접선 또는 b g ∩ {\ displaystyle g\cap {\mathcal {Q} 1\;}, {\displaystyle g} 접선 또는 c) g ∩ Q 2 {\ displaystyle g\cap {\mathcal {Q} =2\;}, {\displaystyle g} secant line 이라 한다. 증명: U u → {\ displaystyle g} Q {\ displaystyle {\mathcal {Q} . U=\langle {\ vec {u}}\rangele \} 와 = → ⟩ v ⟩ displaystyle V =\langle {\v }\rangele \} displaysty g} . q ( u → 0 } q ( x u → + v → ) = q ( x u → ) + q ( v → ) + f ( x u → , v → ) = q ( v → ) + x f ( u → , v → ) . {\displaystyle q(x{\vec{u}+{\vec{v}})=q(x{\vec {u}}+f(x{\vec {u},{\vc{v}})+f(x{\vec}}=q({\vc{v}}}}}}+vec{vec};; } I) In case of g ⊂ U ⊥ {\displaystyle g\subset U^{\perp }} f ( u → , v → ) = 0 {\displaystyle f({\vec {u}},{\vec {v}})=0} q ( x u → + v → ) = q ( v → ) {\displaystyle \;q(x{\vec {u}}+{\vec {v}})=q({\vec {v}})\;} x ∈ K {\displaystyle x\in K} ce either q ( x u → + v → ) = 0 {\displaystyle \;q(x{\vec {u}}+{\vec {v}})=0\;} any x ∈ K {\displaystyle x\in K} q ( x u → + v → ) ≠ 0 {\displaystyle \;q(x{\vec {u}}+{\vec {v}})\neq 0\;} any x ∈ K {\displaystyle x\in K} II) In case of g ⊄ U ⊥ {\displaystyle g\not \subset U^{\perp }} f ( u → , v → ) ≠ 0 {\displaystyle f({\vec {u}},{\vec {v}})\neq 0} q ( x u → + v → ) = q ( v → ) + x f ( u → , v → ) = 0 {\displaystyle \;q(x{\vec {u}}+{\vec {v}})=q({\vec {v}})+xf({\vec {u},{\vec{v}=0\;} 정확히 displaystyle x} : g { displaystyle g\cap mathcal{Q} 2
추가로 그 증거는 다음을 보여준다.
점 P ∈ Q {\ displaystyle P\in {\mathcal {Q} 선 {\displaystyle g^{\perp g ⊂ P ⊥ {\ displaystystyle g^{\p }} 접선 이다. f-11, q-11 고전적인 사례에서 K R {\ displaystyle =\mathb {R} 또는 {\ displaystyle \mathb {C}}은( char 2 {\displaysty \operatorname {char} \ neq 2 } 및 f {\ displaystyty 으) char K {\displaystyle \operatorname {char} K=2} 4중 {\ displaystyle {\mathcal {Q}} 위 {\displaystyf f}
a) R := P ∈ P ⊥ P } {\displaystyle {\R}:=\{P\in {\mathcal}\mid P^{\perp }={\mathcal }\}}}}}}}}}} R {\ displaystyle {\mathcal {R}} Q {\ displaystyle {\mathcal {Q} f-라디칼 이라고 한다. b) S := R ∩ {\ displaystyle {\mathcal {S}:={\mathcal{R}\cap{\mathcal{Q}}}}} {\ displaystyle q} -radical of Q displaystystylease {\\\mathcal{Q} . c) char K ≠ 2 {\displaystyle \operatorname {char} K\neq 2} 경우 S {\ displaystyle {\mathcal{R}={\mathcal {S}} . S ∅ {\displaystyle {\mathcal{S}=\emptyset } 사분면체라고 한다.
P 2 K {\displaystyle P_{2}(K)} 예((E1): For q ( x → ) = x 1 x 2 − x 3 2 {\displaystyle \;q({\vec {x}})=x_{1}x_{2}-x_{3}^{2}\;} f ( x → , y → ) = x 1 y 2 + x 2 y 1 − 2 x 3 y 3 . {\displaystyle f({\vec {x}},{\vec {y}})=x_{1}y_{2}+x_{2}y_{1}-2x_{3}y_{3}\;. } char K ≠ 2 {\displaystyle \operatorname {char} K\neq 2 절대 {\ displaystyle mathcal P} . R S ∅ {\displaystystyle {\\R}={\mathcal}}={S}}}}=\mathcalmet }}}. In case of char K = 2 {\displaystyle \operatorname {char} K=2} f ( x → , y → ) = x 1 y 2 + x 2 y 1 {\displaystyle f({\vec {x}},{\vec {y}})=x_{1}y_{2}+x_{2}y_{1}\;} R = ⟨ ( 0 , 0 , 1 ) T ⟩ ∉ Q {\displaystyle {\mathcal {R}}=\langle (0,0,1)^{\text{ T}}\rangele \notin{\mathcal{Q R ≠ ∅. {\displaystyle {\mathcal{R}\neq{\mathcal{S}=\emptysset \}} 매듭 이다. 두 경우 모두 S ∅ {\displaystyle =\emptyset } 비감소 되지 않는다. (E2): For q ( x → ) = x 1 x 2 {\displaystyle \;q({\vec {x}})=x_{1}x_{2}\;} f ( x → , y → ) = x 1 y 2 + x 2 y 1 {\displaystyle f({\vec {x}},{\vec {y}})=x_{1}y_{2}+x_{2}y_{1}\;} R = ⟨ ( 0 , 0 , 1 ) T ⟩ = S , {\displaystyle {\mathca l {R}=\langle(0,0,1)^{\text{ T}\rangele ={\mathcal{S}\,} 이 예에서는 사면이 퇴화 된다.
대칭 사분위는 다소 동질적인 물체다.
For any point P ∉ Q ∪ R {\displaystyle P\notin {\mathcal {Q}}\cup {\mathcal {R}}\;} involutorial central collineation σ P {\displaystyle \sigma _{P}} P {\displaystyle P} σ P ( Q ) = Q {\displaystyle \sigma _{P}({\mathcal {Q}})={\mathcal {Q}}} 교정: P ∉ ∪ R {\ displaystyle P\notin {\mathcal{Q}\cup{\mathcal{R}}} P ⊥ {\ displaystyle ^{\perp}}}}
선형 매핑
φ : x → → x → − f ( p → , x → ) q ( p → ) p → {\displaystyle \varphi :{\vec{x}}\오른쪽 화살표 {\vec}-{\frac {f({\vec {p},{\vec {p}}}{q\\vec {p}}}{\vec {p}}}}}{\vec {p}}}}}}}}}}}} 축 P ⊥{\ displaystyle ^{\perp }} 중심 P {\displaystyle 비자발적인 중심 결합 ation {\displaystyle } {\displaystystyle Q}}}} In case of char K ≠ 2 {\displaystyle \operatorname {char} K\neq 2} φ {\displaystyle \varphi } familiar shape φ : x → → x → − 2 f ( p → , x → ) f ( p → , p → ) p → {\displaystyle \;\varphi :{\vec {x}}\rightarrow {\vec {x}}-2{\frac {f({\vec {p}},{\vec {x}})}{ f({\vec {p}},{\vec {p}})}}{\vec {p}}\;} φ ( p → ) = − p → {\displaystyle \;\varphi ({\vec {p}})=-{\vec {p}}} φ ( x → ) = x → {\displaystyle \;\varphi ({\vec {x}})={\vec {x}}\;} ⟨ x → ⟩ ∈ P ⊥ {\displaystyle \langle {\vec {x}}\rangle \in P^{\perp }}
비고:
a) 외부 라인, 접선 라인 또는 세컨트 라인은 각각 외부, 접선 및 세컨트 라인의ution P {\ displaystyle \sigma _{P} b) R {\ displaystyle {\mathcal{R}} p displaystyle \sigma _{P} . q-subspace 및 4분위수 색인 U ⊂ Q {\ displaystyle \;{\ mathcal {U}\}; n ( K){\displaystyle P_ {n }}} 하위 {\displaystyle \;{\mathcal {U}\subset {Q};};} 한다
예를 들어, 하이퍼볼로이드 (아래)의 구 또는 선 의 점.
두 개의 최대 q {\displaystyle q} 치수 {\displaystyle m} . [5] 그런 최대 displaystyle } displaystyle mathcal displaystyle m }
정수 i := m 1 {\ displaystyle \;i:=m+1\;} Q {\ displaystyle {\mathcal {Q} 인덱스 라고 한다. 정리: (BUEKENHOUT)[6]
P n K {\displaystyle P_{n}(K)} 4중 displaystyle mathcal {Q}} i {\displaystystyle i} i ≤ n 1 2 {\ displaystyle i\leq {\frac {n+1}{2}}:} Q {\ displaystyle {\mathcal{ Q }} n , n ≥ 2 {\displaystyle P_{n}(K), n \geq 2 } {\displaystyle }
i 1 {\displaystyle =1} Q {\ displaystyle {\mathcal{Q}} 또는 n {\displaystyn=2 타원형 원뿔)라고 한다i 2 {\displaystyle i=2} Q {\ displaystyle {\mathcal{Q}} 하이퍼볼로이드 라고 한다예:
a) Quadric Q {\displaystyle {\mathcal {Q}}} P 2 ( K ) {\displaystyle P_{2}(K)} q ( x → ) = x 1 x 2 − x 3 2 {\displaystyle \;q({\vec {x}})=x_{1}x_{2}-x_{3}^{2}\;} b) 다항식 p ξ ξ 2 0 b 0 {\ displaystyle \;p(\xi )=\xi ^{2}+a_{0 }\xi +b_{0 }\;} K {\displaystyle } 대해 q ( x → 0 1 x 2 b 0 x 23 x {\ displaysty \;q({\vec{x}}})=x_{0}^{0}x_{0} {2+}b_{0 }x_{2}^{2}-x_{3}x_{4}\;} 3 (K {\displaystyle P_{3}(K)} Q {\ displaystystyle {\mathcal{Q}}}}}} 예를 들어, p ξ ξ 2 {\ displaystyle p(\xi )=\xi }+1\;} R {\ displaystyle \mathb {R}}}( C {\ displaysty \mathb {C}!) c) P 3 K {\displaystyle P_{3}(K)} Q( x 1 2 x 3 4 {\ displaysty \;q({\vec{x}}})=x_{1}x_{2}+x_{ 3 }x_{4}\;} 하이퍼볼로이드 를 생성함사분면의 일반화: 이차 집합 정품 꼬치장(분할 고리)을 넘어 공간에 사분면의 정의를 공식적으로 확장하는 것은 합리적이지 않다. 왜냐하면 보통 사분위와는 전혀 다른 사분위수를 2개 이상 붙일 수 있기 때문이다.[7] [8] [9] 그 이유는 다음과 같다.
디비전 링 displaystyle 어떤 방정식 x a b 0 , a b k displaystyle ^{2}+ax+b=0,\in } ) 대응적 이다4차원의 일반화 가 있다: 2차적 집합 .[10] 2차 집합은 4차원과 동일한 기하학적 특성을 가진 투영 공간의 점 집합이다. 모든 선은 2차 집합을 교차하거나 집합에 포함된다.
참고 항목 참조 ^ "지오메트리 공식 및 사실"의 실비오 레비 사분법 , 미네소타 대학교 기하학 센터에서 CRC 표준 수학적 표와 공식 , CRC 프레스 30판에서 발췌함 ^ Stewart Venit and Wayne Bishop, 초등 선형 대수학 (4판), International Thompson Publishing, 1996.^ S. 라제브닉과 J. 폰세 "The Local Projective Shape of Smooth Surfaces and Their Outlines" (PDF) .^ 부텔스파커/로센바움: 158페이지 ^ 뷰텔파허/로센바움, 페이지 139 ^ F. Buekenhout: 앙상블 쿼드래티크 데 에스페이스 프로젝트ive , 수학. Teitschr. 110 (1969), 페이지 306-318. ^ R. Artzy : 코닉 2 {\ displaystyle y=x^{2}} Moufang , Aequat. 매템 6(1971년), 페이지 31-35 ^ E. Berz: 수학의 데스카게스첸 에베넨 에 있는 케겔슈니트 . Zeitschr 78 (1962년), 페이지 55-8 ^ 외부 링크 E. 하트만: Planar Circle Geometries , 페이지 123 ^ Beutelspacher/Rosenbaum: 페이지 135
참고 문헌 목록 오딘: 지오메트리 , 스프링거, 2002년 베를린, ISBN 978-3-540-43498-6 , 페이지 200. M. Berger: 수학 문제집 , ISSN 0941-3502, Springer New York, 페이지 79–84. A. Beutelspacher, U. Rosenbaum: Projektive Geometrie , Vieweg + Teubner, Brounschweig u. a. 1992년 ISBN 3-528-07241-5 , 페이지 159. P. 뎀보스키: 유한 기하학 , 스프링거, 1968, ISBN 978-3-540-61786-0 , 페이지 43. Iskovskikh, V.A. (2001) [1994], "Quadric" , Encyclopedia of Mathematics EMS Press Weisstein, Eric W. "Quadric" . MathWorld 외부 링크 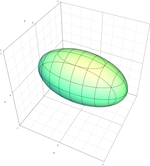





















 경우 1개가 이중 평면을 가지고 있다.
경우 1개가 이중 평면을 가지고 있다. 

































 때 가정한다
때 가정한다










 (는)
(는) 





















 (를)
(를) 




 (는) 대칭이다.
(는) 대칭이다. 















 ,
,










 경우 x
경우 x 


















 (
(



























 (원뿔) 사면이 비감소되지 않는다.
(원뿔) 사면이 비감소되지 않는다.



 하이퍼플레인이다
하이퍼플레인이다













 (는)
(는) 





 Planes, Aequat.매템 6(1971년), 페이지 31-35
Planes, Aequat.매템 6(1971년), 페이지 31-35

