테트라데카곤

정사각형
정사각형
유형	정규 다각형
모서리 및 정점	14
슐레플리 기호	{14}, t{7}
콕시터-딘킨 도표
대칭군	디헤드랄(D14), 2×14 주문
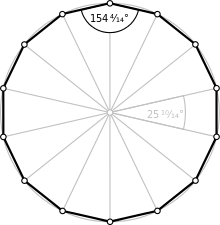
내부 각도(도)	154+2/7°
특성.	볼록, 주기, 등변, 이등변, 동위원소

기하학에서 4각형 또는 4각형 또는 14각형은 14면 다각형이다.

정사각형

일반 테트라데카곤은 슐래플리 기호 {14}을(를) 가지며, 두 가지 유형의 가장자리를 교대로 하는 헵타곤, t{7}로 구성할 수 있다.

측면 길이 a의 정규 4각형 영역은 다음과 같다.

${\displaystyle A={\frac {14}{4}}a^{2}\cot {\frac {\pi }{14}}}\약 15.3345a^{2}}:$

건설

14 = 2 × 7이므로, 일반 사선각은 나침반과 직선자를 사용하여 구성할 수 없다.^[1] 단, 다음 두 가지 예와 같이 각도 삼지경을 사용하거나, 표시된 자를 ^[2]사용하여 네우스(neusis)를 이용하여 구성할 수 있다.^[3]

대칭

일반 테트라데카곤은 Dih₁₄ 대칭, 순서 28. 3개의 부분군 분면 대칭이 있다. Dih₇₁₄, Dih₂, Dih₁ 및 4개의 순환 그룹 대칭: Z, Z₂, Z₇₁.

이 8개의 대칭은 정점이나 가장자리를 통과할 수 있기 때문에 더 큰 숫자인 4각형의 10개의 뚜렷한 대칭에서 볼 수 있다. 존 콘웨이는 편지와 단체 주문으로 이것들에 라벨을 붙였다.^[4] 정규형식의 전체 대칭은 r28이며 어떤 대칭도 a1로 표기되지 않는다. 이음 대칭은 정점(대각의 경우 d) 또는 가장자리(직각의 경우 p)를 통과하는지와 반사선이 양쪽 가장자리와 정점을 통과했을 때 i에 따라 구분된다. 중앙 열의 주기적 대칭은 중심 교량 순서에 대해 g로 표시된다.

각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다. g14 부분군만 자유도는 없지만 지시된 가장자리로 볼 수 있다.

가장 높은 대칭 불규칙한 테트라데카곤은 d14로 길고 짧은 가장자리를 교대할 수 있는 7개의 거울에 의해 구성된 이등변 테트라데카곤과 가장자리 길이가 같지만 정점이 두 개의 내부 각도를 교대하는 동위원소 테트라데카곤이다. 이 두 형태는 서로 이중으로 되어 있으며, 정사각형의 대칭 순서의 절반을 가지고 있다.

해부

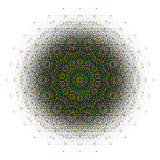14구경 투영법

84 롬브 해부

Coxeter는 모든 조노곤(상대방이 평행하고 길이가 같은 2m-곤)을 m(m-1)/2 평행그램으로 해부할 수 있다고 명시하고 있다.^[5] 특히 면적이 고르게 많은 일반 다각형의 경우, 이 경우 평행사변형은 모두 rhombi이다. 일반 테트라데카곤의 경우 m=7이며, 7 rhomb의 21:3 세트로 나눌 수 있다. 이 분해는 페트리 폴리곤 7큐브 투영을 기반으로 하며, 672면 중 21면이다. OEIS: A006245 목록에는 반영되어 있는 14배 회전 및 키랄 형태를 포함하여 24698개의 솔루션으로 정의되어 있다.

21마리의 늑대로 해부한다.

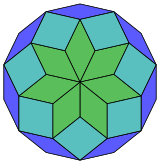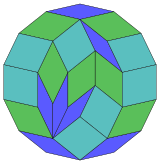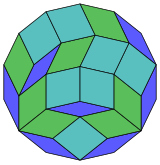숫자 사용법

일반 테트라데카곤은 말레이시아 연방의 14개 주를 대표하는 면의 수인 일부 기념 금화와 은화의 형태로 사용된다.^[6]

관련숫자

테트라데카그램은 기호가 {14/n}인 14면 별 다각형이다. 두 개의 일반 별 다각형이 있다: {14/3}과(와) {14/5}, 같은 정점을 사용하지만 3번째 또는 5번째 지점마다 연결된다. 또한 세 가지 화합물이 있는데, {14/2}은(는) 2개의 헵타곤으로 2{7}, {14/4}과(와) {14/6}은(는) 2{7/2}, 2{7/3}은(는) 2개의 서로 다른 헵타로 축소되고, 마지막으로 {14/7}은(는) 7개의 디곤으로 축소된다.

14점짜리 별의 주목할 만한 적용은 말레이시아 국기에 있는데, 이 깃발은 오른쪽 상단 모서리에 노란색 {14/6} 테트라데카그램이 통합되어 연방정부와 13개 주가 단결을 나타낸다.

화합물 및 항성 다각형
n	1	2	3	4	5	6	7
형태	정규	화합물	별 폴리곤	화합물	별 폴리곤	화합물
이미지	{14/1} = {14}	{14/2} = 2{7}	{14/3}	{14/4} = 2{7/2}	{14/5}	{14/6} = 2{7/3}	{14/7} 또는 7{2}
내부 각도	≈154.286°	≈128.571°	≈102.857°	≈77.1429°	≈51.4286°	≈25.7143°	0°

정규 헵타곤과 헵타그램의 더 깊은 절단은 정점과 두 개의 가장자리 길이의 등각형 중간 테트라다그램 형태를 생성할 수 있다. 다른 절단은 폴리곤 2{p/q}, 즉 t{7/6}={14/6}=2{7/3}, t{7/4}={14/4}=2{7/2}, t{7/2}={14/2}={14/2}={7}}.^[7]

헵타곤과 헵타의 등각 절단
퀘이레굴라속	등각			퀘이레굴라속 이중 커버
t{7}={14}		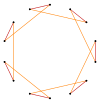		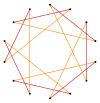{7/6}={14/6} =2{7/3}
t{7/3}={14/3}				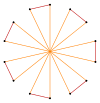t{7/4}={14/4} =2{7/2}
t{7/5}={14/5}				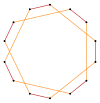t{7/2}={14/2} =2{7}

동위원소 형태

동위원소 폴리곤은 바깥쪽 가장 내부 각도가 α인 {p_α}, 그리고 q가 권선 번호인 별 폴리곤 {(p/q)},_α gcd(p,q)=1, q<p)로 라벨을 붙일 수 있다. 동위원소 테트라데카곤은 p=7을 가지고 있고, 7이 최상이므로 모든 해결책인 q=1..6은 폴리곤이다.

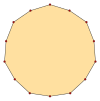{7α}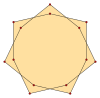

{(7/2)α}

{(7/3)α}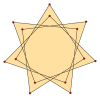

{(7/4)α}

{(7/5)α}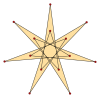

{(7/6)α}

페트리 폴리곤

일반 스큐 테트라데카곤은 많은 고차원 폴리탑에 대해 Petrie 폴리곤으로 존재하며, 다음을 포함한 이러한 스큐 직교 투영에서 볼 수 있다.

페트리 폴리곤
B7		2I2(7)(4D)
7형식	7시 15분	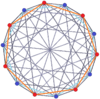7-7 듀오피라미드	7-7 듀오프리즘
A을13	D8		E8
13xx	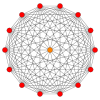511	151	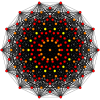421	241

참조

외부 링크

• Weisstein, Eric W. "Tetradecagon". MathWorld.