사비츠키-골레이 필터

사비츠키-골레이 필터는 디지털 데이터 포인트 집합에 적용할 수 있는 디지털 필터로 신호 경향을 왜곡하지 않고 데이터의 정밀도를 높일 수 있다.이것은 콘볼루션이라고 알려진 프로세스에서 선형 최소 제곱법에 의해 저도 다항식으로 인접 데이터 점의 연속 하위 집합을 적합시킴으로써 달성된다.데이터 포인트의 간격이 같을 경우, 모든 데이터 서브셋에 적용할 수 있는 단일 집합의 "콘볼루션 계수"의 형태로 최소 제곱 방정식에 대한 분석 솔루션을 찾아 각 서브셋의 중앙점에 평활 신호 또는 평활 신호의 파생 모델의 추정치를 제공할 수 있다.이 방법은 확립된 수학적 절차를 바탕으로 1964년 아브라함 사비츠키(Abraham Savitzky)와 마르셀 J. E. Golay(Marcel J. Golay)^[3][4]에 의해 대중화되었다.^[1][2]표의 몇 가지 오류가 수정되었다.^[5]2차원 및 3차원 데이터 처리를 위한 방법이 확장되었다.

사비츠키와 골레이의 논문은 분석 화학^[6] 저널에서 가장 널리 인용된 논문 중 하나이며, 이 저널에 의해 "컴퓨터가 제어하는 분석 기구의 새벽을 이 기사로 추적할 수 있다고 주장할 수 있다"는 10개의 논문의 하나로 분류된다.^[7]

적용들

데이터는 점 집합 {x_j, y_j}, j = 1, ..., n으로 구성되며 여기서 x는_j 독립 변수, y는_j 관측값이다.그것들은 표현에 따라 일련의 m 콘볼루션 계수 C로_i 처리된다.

${\displaystyle Y_{j}=\sum _{i={1-m}{2}}^{\tfrac {m-1}\{2}}C_{{i}\,y_{j+i},\qd{\frac {\m+1}{2}}:00}$

선택된 콘볼루션 계수는 아래 표에 표시된다.예를 들어 5점 2차 다항식으로 평활하는 경우 m = 5, i = -2, -1, 0, 1, 2 및 j번째 평활 데이터 점 Y는_j

${\displaystyle Y_{j}={\frac {1}{35}}(-3y_{j-2}+12y_{j-1}+17y_{j}+12y_{j+1}-3y_{j+2})}$,

여기서, C₋₂ = -3/35, C₋₁ = 12/35 등평활화에는 수많은 응용이 있는데, 주로 데이터가 실제보다 덜 시끄러운 것처럼 보이도록 하기 위해 수행된다.다음은 데이터의 수치적 분화 적용이다.^[8]참고 n번째 파생상품을 계산할 때 $n{\displaystyle \frac{!}{h^{}}}$ ${\$$}{h^{n}}}}}}}}}}}}$은(${\displaystyle \frac{{아래}^{}}{}}$에서 ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{Y^{}}{}}$ d$$x n {\$디스플레이스타일${\$d^{n}Y}{dx^{n$을(를) 얻기 위해 계산된 모든 데이터 포인트에 적용할$$ 수 있다.

1. 실험 데이터 곡선에서 최대값과 최소값의 위치.이것이 사비츠키에게 처음으로 동기를 부여한 애플리케이션이었다.^[4]함수의 첫 번째 파생상품은 최대 또는 최소로 0이다.다이어그램은 노이즈(블루 다이아몬드)가 추가된 합성 로렌츠 곡선에 속하는 데이터 포인트를 보여준다.데이터는 0에서 최대값을 기준으로 반 폭의 척도로 표시된다.평활 곡선(빨간색 선)과 1차 파생 모델(녹색)은 7포인트 큐빅 사비츠키-골레이 필터로 계산했다.제로 크로싱의 어느 한쪽 위치에서 첫 번째 파생상품 값의 선형 보간법은 최대 피크 위치를 제공한다.제3차 파생상품도 이러한 목적으로 사용할 수 있다.
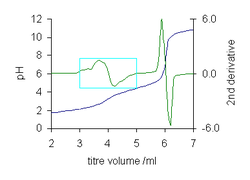
2. 적정 곡선의 끝점 위치.끝점은 함수의 두 번째 파생상품이 0인 변곡점이다.^[9]말론산에 대한 적정곡선은 방법의 힘을 보여준다.첫 번째 끝점은 4ml로 거의 보이지 않지만, 두 번째 파생상품은 제로 크로스를 찾기 위해 선형 보간법으로 쉽게 그 가치를 결정할 수 있다.
3. 기준 평탄화.해석 화학에서는 때때로 곡선 기준선에 대한 흡수 밴드의 높이를 측정해야 한다.^[10]기준선의 곡률이 흡수대 곡률보다 훨씬 작기 때문에 두 번째 파생상품은 효과적으로 기준선을 평평하게 만든다.흡수대 높이와 비례하는 파생상품 높이의 세 가지 척도는 "피크 대 밸리" 거리 h1과 h2와 기준선으로부터의 높이 h3이다.^[11]
4. 분해능 향상 분광기.스펙트럼 분석 곡선의 두 번째 파생상품의 대역은 스펙트럼의 대역보다 좁다. 즉, 반폭을 줄였다.이를 통해 부분적으로 겹치는 밴드를 별도의 (음극) 피크로 "해결"할 수 있다.^[12]다이어그램은 "피크 대 밸리" 거리 측정을 사용하여 화학적 분석에 어떻게 사용될 수 있는지를 보여준다.이 경우, 계곡은 로렌츠인의 두 번째 파생상품의 특성이다. (x축 위치는 절반 높이에서 절반 너비의 눈금에서 피크 최대값의 위치에 상대적이다.)
5. 4번째 파생 모델로 분해능 향상(양극 피크)미니마는 로렌츠인의 4번째 파생상품의 특성이다.

이동평균

이동 평균 필터는 단기 변동을 완화하고 장기 추세 또는 주기를 강조하기 위해 시계열 데이터와 함께 일반적으로 사용된다.그것은 종종 주가, 수익률 또는 거래량과 같은 재무 데이터의 기술적 분석에 사용된다.또한 국내 총생산, 고용 또는 기타 거시경제 시계열을 조사하는 데 경제 분야에서도 사용된다.

가중치가 없는 이동 평균 필터는 가장 간단한 콘볼루션 필터다.데이터 세트의 각 부분 집합은 직선 수평선에 의해 적합된다.모든 계수 값이 단순히 다음 값과 같기 때문에 콘볼루션 계수의 사비츠스키-골레이 표에는 포함되지 않았다.1/m.

콘볼루션 계수 도출

데이터 점의 간격이 같을 경우 최소 제곱 방정식에 대한 분석 솔루션을 찾을 수 있다.^[2]이 용액은 수치 평활과 분화의 콘볼루션 방법의 기초를 형성한다.데이터가 n개의 점 집합(x_jj, y)으로 구성되어 있다고 가정하자(j = 1, ..., n), 여기서 x는_j 독립 변수, y는_j 기준값이다.다항식은 각각 구간 h로 구분된 m(홀수) 인접 데이터 점 집합에 선형 최소 제곱으로 적합된다.첫째, 변수의 변화가 일어난다.

${\displaystyle z={{x-{\bar {x}} \over h}}}}$

where ${\displaystyle {\bar {x}}}$ is the value of the central point. z takes the values ${\displaystyle {\tfrac {1-m}{2}},\cdots ,0,\cdots ,{\tfrac {m-1}{2}}}$ (e.g. m = 5 → z = −2, −1, 0, 1, 2).^{[note 1]}도 k의 다항식은 다음과 같이 정의된다.

${\displaystyle Y=a_{0}+a_{1}z+a_{2}z^{2}\cdots +a_{k}z^{k}.}$^[주2]

계수 a₀, a₁ 등은 정규 방정식을 풀어서 구한다(bold a는 벡터를, 굵은 J는 행렬을 나타낸다).

${\displaystyle {\mathbf {a} }=\left({{\mathbf {J} }^{\mathbf {T} }{\mathbf {J} }}\right)^{-{\mathbf {1} }}{\mathbf {J} }^{\mathbf {T} }{\mathbf {y} },}$

여기서 $J{\displaystyle \mathbf{}}$ ${\$은(는) Vandermonde 행렬로, $즉{\displaystyle \mathbf{}}$ J$$${\$$displaystyle \mathbf {J}$의 세 번째 행에는 값 $1{\displaystyle \mathrm{}}$,${\displaystyle {}_{}^{}{}_{}{i}_{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$,${\displaystyle }$…$${\$displaysty$1$, z_{i$}z_{i$}^{2}, dots }$가 있다$$$.$

예를 들어, 5점에 맞는 입방 다항식의 경우, z= -2, -1, 0, 1, 2의 정규 방정식은 다음과 같이 해결된다.

${\displaystyle \mathbf{J} ={\begin{pmatrix}1&-2&4-8\\1&1&1&1&1&0\1&0\1&1&1&1\&1&4&8\end{pmatrix}}}}}}$

${\displaystyle \mathbf {J^{T}J}={\begin{pmatrix}m&, \sum z&, \sum z^{2}&, \sum z^{3}\\\sum z&, \sum z^{2}&, \sum z^{3}&, \sum z^{4}\\\sum z^{2}&, \sum z^{3}&, \sum z^{4}&, \sum z^{5}\\\sum z^{3}&, \sum z^{4}&, \sum z^{5}&, \sum z^{6}\\\end{pmatrix}}={\begin{pmatrix}m&, 0&,\sum z^{2}&, 0\\0&,\sum z^{2}&, 0&,\sum z^{4}\\\sum z^{2}&, 0&.앰프,\sum z^{4}&, 0\\0&,\sum z^{4}&, 0&, \sum z^{6}\\\end{pmatrix}}={\begin{pmatrix}5&, 0&.10&0\\0&10&34\\10&0&34\\10&34&0\\0&34&0&130\\end{pmatrix}}}$

이제, 정규 방정식은 행과 열을 재배열하여 다음과 같은 두 개의 개별적인 방정식으로 나눌 수 있다.

${\displaystyle \mathbf {J^{T}J} _{\text{ven}={\begin{pmatrix}5&10\\10&34\\\end{pmatrix}\quad \mathrm {and}\quad \quad \mathbf {J^{{}}T}J} _{\text{odd}={\begin{pmatrix}10&34\\34&130\\end{pmatrix}}}}$

이러한 행렬의 각 행렬의 역행 표현식은 Cramer의 규칙을 사용하여 얻을 수 있다.

${\displaystyle(\mathbf {J^{)T}J} )_{\text{J^{-1}^{-1}={1 \\begin{pmatrix}34&-10\-10&5\\\end{pmatrix}\quad \mathrm {and} \mathbf {J^{{}}}T}J} )_{\text{odd}^{-1}={1 \1 \over 144}{\begin{pmatrix}130&-34\-34&10\\\end{pmatrix}}}}}$

정규 방정식이 된다.

${\displaystyle {\begin{pmatrix}{a_{0}}\\{a_{2}}\\\end{pmatrix}}_{j}={1 \over 70}{\begin{pmatrix}34&-10\\-10&5\end{pmatrix}}{\begin{pmatrix}1&1&1&1&1\\4&1&0&1&4\\\end{pmatrix}}{\begin{pmatrix}y_{j-2}\\y_{j-1}\\y_{j}\\y_{j+1}\\y_{j+2}\end{pmatrix}}}$

그리고

${\displaystyle {\begin{pmatrix}a_{1}\\a_{3}\\\end{pmatrix}}_{j}={1 \over 144}{\begin{pmatrix}130&-34\\-34&10\\\end{pmatrix}}{\begin{pmatrix}-2&-1&0&1&2\\-8&-1&0&1&8\\\end{pmatrix}}{\begin{pmatrix}y_{j-2}\\y_{j-1}\\y_{j}\\y_{j+1}\\y_{j+2}\\\end{pmatrix}}}$

다중화 및 공통 요인 제거,

${\displaystyle {\begin{aligned}a_{0,j}&={1 \over 35}(-3y_{j-2}+12y_{j-1}+17y_{j}+12y_{j+1}-3y_{j+2})\\a_{1,j}&={1 \over 12}(y_{j-2}-8y_{j-1}+8y_{j+1}-y_{j+2})\\a_{2,j}&={1 \over 14}(2y_{j-2}-y_{j-1}-2y_{j}-y_{j+1}+2y_{j+2})\\a_{3,j}&={1 \over 12}(-y_{j-2}+2y_{j-1}-2y_{j+1}+y_{j+2})\end{aligned}}}$

이러한 표현에서 y의 계수는 콘볼루션 계수로 알려져 있다.그것들은 행렬의 요소들이다.

${\displaystyle \mathbf {C=(J^{T}J)^{-1}J^{T}} }$

대체적으로.

${\displaystyle (C\otimes y)_{j}\ =Y_{j}=\sum _{i=-{\tfrac {m-1}{2}}}^{\tfrac {m-1}{2}}C_{i}\,y_{j+i},\qquad {\frac {m+1}{2}}\leq j\leq n-{\frac {m-1}{2}}}$

행렬 표기법에서 이 예는 다음과 같이 기록된다.

${\displaystyle {\pmatrix}Y_{3}\\Y_{4}\\Y_{5}\\\vdots};12&, 17&, 12&, -3&, 0&, 0&, \cdots \\0&, -3&, 12&, 17&, 12&, -3&, 0&, \cdots \\0&, 0&, -3&, 12&, 17&, 12&, -3&, \cdots \\\vdots &, \vdots &, \vdots &, \vdots &, \vdots &, \vdots &, \vdots &, \ddots}{\begin{pmatrix}y_{1\end{pmatrix}={1\over 35}{\begin{pmatrix}-3& \end{pmatrix}.}}\end{pmatrix}\\y_{2}\\y_{3}\\y_{4}\\y_{5}\\y_{6}\\y_{7}\\\vdots}$

m ~ 25에 대해 동일한 방법으로 계산된 콘볼루션 계수 표는 1964년에 사비츠키-골레이 스무딩 필터에 대해 발행되었다.^[3][5] 중심점 값 z = 0은 단일 계수 집합, 평활용 a₀, 첫 번째 파생상품 등에₁ 대해 구한다.수치적 파생상품은 Y를 구별하여 얻는다.이는 파생상품이 평활 데이터 곡선에 대해 계산된다는 것을 의미한다.입방 다항식의 경우

${\displaystyle {\reasoned}Y&, =a_{0}+a_{1}z+a_{2}z^{2}+a_{3}z^{3}=a_{0}&,{\text{에서}}z=0,x={\bar{)}}\\{\frac{dY}{dx}}&={\frac{1}{h}}\left({a_{1}+2a_{2}z+3a_{3}z^{2}}\right)={\frac{1}{h}}a_{1}&,{\text{에서}}z=0,x={\bar{)}}\\{\frac{{2d^}Y}{dx^{2}}}&={\frac{1}{h^{2}}}\left({2a_{2}+6a_{3}z}\right)={\frac{2}{h^{2}}}a_{2}&,{\text{에서}}z=0,x={\bar{)}}.\\{\frac{d^{3}Y}{dx^{3}}}&={\frac {6}{h^{3}}a_{3}\ended{정렬}}}}}}}$

일반적으로 도(0과 1),^{[note 3]} (2와 3), (4와 5) 등의 다항식은 평활화 및 짝수파생물에 대해 동일한 계수를 제공한다.도(1과 2), (3과 4) 등의 다항식은 홀수 유도체에 대해 동일한 계수를 제공한다.

대수적 표현식

사비츠키-골레이 테이블을 항상 사용할 필요는 없다.매트릭스 JJ의^T 합계는 폐쇄된 형태로 평가될 수 있다.

${\displaystyle {\begin{aligned}\sum _{z=-{\frac {m-1}{2}}}^{\frac {m-1}{2}}z^{2}&={m(m^{2}-1) \over 12}\\\sum z^{4}&={m(m^{2}-1)(3m^{2}-7) \over 240}\\\sum z^{6}&={m(m^{2}-1)(3m^{4}-18m^{2}+31) \over 1344}\end{aligned}}}$

대수적 공식은 경련 계수에 대해 도출될 수 있다.^{[13][note 4]}변곡점이 있는 곡선과 함께 사용하기에 적합한 함수는 다음과 같다.

Smoothing, polynomial degree 2,3 : ${\displaystyle C_{0i}={\frac {\left({3m^{2}-7-20i^{2}}\right)/4}{m\left({m^{2}-4}\right)/3}};\quad {\frac {1-m}{2}}\leq i\leq {\frac {m-1}{2}}}$ (the range of values for i also applies 아래 표현에 대해)

1st derivative: polynomial degree 3,4 ${\displaystyle C_{1i}={\frac {5\left({3m^{4}-18m^{2}+31}\right)i-28\left({3m^{2}-7}\right)i^{3}}{m\left({m^{2}-1}\right)\left({3m^{4}-39m^{2}+108$$}\오른쪽)/15}$

2차 파생상품: 다항식도 C ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle i_{}}$= ${\displaystyle \frac{12}{}}$ ${\displaystyle \frac{m}{}}$ ${\displaystyle \frac{i}{}}$ 2${\displaystyle \frac{{}^{}}{}}$- m${\displaystyle \frac{}{}}$( ${\displaystyle \frac{m{}^{}}{}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{{}^{}}}$- ${\displaystyle \frac{1}{}}$) ${\displaystyle \frac{{m\mathrm{}}^{}}{}}$ 2${\displaystyle \frac{{}^{}}{}}$(${\displaystyle \frac{m{}^{}}{}}$ ${\displaystyle \frac{2{}^{}{}^{}}{}}$- ${\displaystyle \frac{1}{}}$)${\displaystyle \frac{}{}}$/ ${\displaystyle \frac{30}{}}$ ${\$$}}{m^{2}\왼쪽 ^{2}-1}\오른쪽)\왼쪽 ^{2}-4}\오른쪽)/30}}$

3차 파생상품: 다항식도 ${\displaystyle C_{}}$ 3 ${\displaystyle {i\mathrm{}}_{}}$ =${\displaystyle {}_{}}$-${\displaystyle \frac{}{}}$(${\displaystyle \frac{{}^{}}{}}$ 2 -${\displaystyle \frac{{}^{}{7\mathrm{}}^{}}{}}$ )${\displaystyle \frac{\mathrm{i}}{}}$ +${\displaystyle \frac{20}{}}$ i ${\displaystyle \frac{{3m\mathrm{}}^{}}{}}$ (${\displaystyle \frac{{}^{}2{}^{}}{}}$ -${\displaystyle \frac{{}^{}1}{}}$ )${\displaystyle \frac{}{}}$/${\displaystyle \frac{3m\mathrm{}}{}}$ 4 -${\displaystyle \frac{{}^{}{39m\mathrm{}}^{}}{}}$ 2${\displaystyle \frac{{}^{}}{}}$+ ${\displaystyle \frac{108}{}}$)${\displaystyle \frac{}{}}$/ $(\$$}}{m\왼쪽 leftm^{2}-1}\오른쪽)\왼쪽 ({3m^{4}-39m^{2}+108}\오른쪽)/420}}}$

변곡점이 없는 곡선과 함께 사용할 수 있는 간단한 표현식은 다음과 같다.

평활, 다항식 도 0.1(이동 평균):${\$

1차 파생 모델, 다항식 도 1,2: C $1{\displaystyle {}_{}}$ ${\displaystyle i_{}}$= i ${\displaystyle \frac{m({m\mathrm{}}^{}}{}}$ 2${\displaystyle \frac{{}^{}}{}}$- ${\displaystyle \frac{1}{}}$)${\displaystyle \frac{}{}}$/ ${\displaystyle \frac{12}{}}$ ${\$

더 높은 파생상품을 얻을 수 있다.예를 들어, 네 번째 파생상품은 두 번째 파생상품 함수의 패스를 두 번 수행하여 얻을 수 있다.^[14]

직교 다항식 사용

보조 변수 z에서 m 데이터 점을 단순 다항식으로 적합시키는 방법의 대안은 직교 다항식을 사용하는 것이다.

${\displaystyle Y=b_{0}P^{0}(z)+b_{1}P^{1}(z)\cdots +b_{k}P^{k}(z).}$

여기서 P⁰, ..., P는^k 0, ..., k의 상호직교 다항식의 집합이다. 직교 다항식의 식을 얻는 방법과 계수 b와 a의 관계에 대한 자세한 내용은 게스트가 제공한다.^[2]정규 방정식 행렬인 JJ는^T 상호 직교성 때문에 두 직교 다항식의 곱이 0이기 때문에 대각 행렬이기 때문에 경련 계수에 대한 식을 쉽게 얻을 수 있다.따라서 역의 각 0이 아닌 원소는 단순히 정규 방정식 행렬에서 대응하는 원소의 역수일 뿐이다.직교 Gram 다항식을 만들기 위해 재귀법을 사용함으로써 계산이 더욱 단순화된다.전체 계산은 재귀와 관련된 계산에 잘 적응된 컴퓨터 언어인 PASCAL의 몇 줄에 코딩될 수 있다.^[15]

첫 번째 및 마지막 점의 처리

사비츠키-골레이 필터는 단일 콘볼루션 계수 집합을 사용하여 중심점 z = 0의 평활값 또는 파생값을 얻기 위해 가장 일반적으로 사용된다.(m - 1)/시리즈의 시작점과 끝점은 이 과정을 이용하여 계산할 수 없다.이런 불편을 피하기 위해 다양한 전략을 활용할 수 있다.

• 데이터는 첫 번째(m - 1)/2 지점의 복사본과 마지막(m - 1)/2 지점의 복사본을 차례로 추가하여 인위적으로 확장할 수 있다.예를 들어 m = 5를 사용하면 데이터 y₁, ..., y의_n 시작과 끝에 두 점이 추가된다.

y₃,y₂,y₁,y,...y_n,y_n−1,y,y,y_n−2.

• 적합한 다항식을 다시 살펴보면, 하나의 다항식, a₀ .. a에_k 대한 모든 합성 계수 집합을 사용하여 z의 모든 값에 대해 데이터를 계산할 수 있다는 것은 명백하다.

입방 다항식의 경우

${\displaystyle {\reasoned}Y&=a_{0}+a_{1}z+a_{2}z^{2}+a_{3}z^{3}\\{\frac {dY}{dx}}&={\frac {1}{h}}(a_{1}+2a_{2}z+3a_{3}z^{2})\\{\frac {d^{2}Y}{dx^{2}}}&={\frac {1}{h^{2}}}(2a_{2}+6a_{3}z)\\{\frac {d^{3}Y}{dx^{3}}}&={\frac {6}{h^{3}}a_{3}\ended{정렬}}}}}}}$

• 누락된 첫 번째 지점과 마지막 지점에 대한 콘볼루션 계수도 쉽게 얻을 수 있다.^[15]이것은 또한 같은 다항식으로 첫 번째 (m + 1)/2 점을 적합시키는 것과 같으며, 마지막 점에도 유사하다.

데이터 가중치 부여

데이터 포인트에 모두 동일한 가중치를 부여한다는 것은 위의 치료법에서 함축되어 있다.기술적으로, 객관적 기능

${\displaystyle U=\sum _{i}w_{i}(Y_{i}-y_{i}^{2}}$

최소 공정에서 최소화되는 단위 중량은 w = 1이다_i.가중치가 모두 같지 않을 때 정규 방정식이 된다.

${\displaystyle \mathbf {a} =\left(\mathbf {J^{T}W} \mathbf {J} \right)^{-1}\mathbf {J^{T}W} \mathbf {y} \qquad W_{i,i}\neq 1}$,

모든 데이터 하위 집합에 대해 동일한 대각선 가중치 집합을 사용하는 경우,${\displaystyle }W{\displaystyle }$ = ${\displaystyle \text{diag}({w\mathrm{}}_{}}$ ${\displaystyle {}_{}}$,${\displaystyle {}_{}{w\mathrm{}}_{}}$ ${\displaystyle {}_{}}$,${\displaystyle }$.${\displaystyle }$. w${\displaystyle {}_{}{m}_{}}$ )$${\$displaystyle W={\text{diag}}}(w_{1},w_{2$}, $..., w_{m}),$ 정상$$방정식에 대한 분석 솔루션을 기록할 수 있다.예를 들어, 2차 다항식에서는

${\displaystyle \mathbf {J^{T}WJ} ={\begin{pmatrix}m\sum w_{i}&\sum w_{i}z_{i}&\sum w_{i}z_{i}^{2}\\\sum w_{i}z_{i}&\sum w_{i}z_{i}^{2}&\sum w_{i}z_{i}^{3}\\\sum w_{i}z_{i}^{2}&\sum w_{i}z_{i}^{3}&\sum w_{i}z_{i}^{4}\end{pmatrix}}}$

이 행렬의 역행렬에 대한 명시적 표현은 크레이머의 규칙을 사용하여 얻을 수 있다.다음과 같이 일련의 콘볼루션 계수를 도출할 수 있다.

${\displaystyle \mathbf {C} =\왼쪽(\mathbf {J^{T}W} \mathbf {J} \right)^{-1}\mathbf {J^{T}W}.}$

또는 계수 C를 스프레드시트에서 계산할 수 있으며, 기본 제공 행렬 반전 루틴을 사용하여 정규 방정식 행렬의 역행렬을 구할 수 있다.일단 계산되고 저장되면 이 계수 집합을 동일한 가중치가 적용되는 모든 계산에 사용할 수 있다.각각의 다른 가중치 체계에는 다른 계수 세트가 필요하다.

2차원 콘볼루션 계수

직사각형 픽셀 그리드로 구성된 사진 영상의 강도 값과 같은 데이터 값 표에도 2차원 평활과 분화를 적용할 수 있다.^[16][17] 이러한 그리드를 커널이라고 하며 커널을 구성하는 데이터 포인트를 노드라고 한다.노드의 지수를 단순 순서에 따라 직사각형 커널을 하나의 행으로 변환하는 것이 요령이다.1차원 필터 계수는 m 데이터 지점 집합에 종속 변수 z의 다항식을 적합시켜 찾지만, 2차원 계수는 m × n 커널 노드의 값 집합에 종속 변수 v와 w의 다항식을 적합시켜 찾는다.다음 예제는 총 도 3, m = 7 및 n = 5의 이바리테 다항식의 경우 위의 1차원 사례에 대한 공정을 병렬하는 과정을 보여준다.^[18]

${\displaystyle v={\frac {x-{\bar{x}}{h(x)}}{w={\frac {y-}{h(y)}}}}}}$

${\displaystyle Y=a_{00}+a_{10}v+a_{01}w+a_{20}v^{2}+a_{11}vw+a_{02}w^{2}+a_{30}v^{3}+a_{21}v^{2}w+a_{12}vw^{2}+a_{03}w^{3}}$

35개₁ 데이터 값의 직사각형 커널, d₃₅ - d

v w	−3	−2	−1	0	1	2	3
−2	d1	d2	d3	d4	d5	d6	d7
−1	d8	d9	d10	d11	d12	d13	d14
0	d15	d16	d17	d18	d19	d20	d21
1	d22	d23	d24	d25	d26	d27	d28
2	d29	d30	d31	d32	d33	d34	d35

행이 차례로 배치될 때 벡터가 된다.

d = (d₁ ... d₃₅)^T

Jacobian은 10개의 열을 가지고 있는데₀₃, 각 변수₀₀ a - a, 그리고 35개의 행을 각 v와 w 값 쌍에 하나씩 가지고 있다.각 행에는 형식이 있다.

${\displaystyle J_{\text{row}=1\quad v\quad ww\quad v^{2}\quad v^{2}\quad v^{3}\quad v^{2}w^{2}\quad vw^{2}\quad ww^{3}\quad w^{3}}}}}}}}}}}}\quad w^{3}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

콘볼루션 계수는 다음과 같이 계산된다.

${\displaystyle \mathbf {C} =\왼쪽(\mathbf {J} ^{T}\mathbf {J} \right)^{-1}\mathbf {J}^{T}}}$

C의 첫 번째 행에는 각각 35개의 데이터 값을 곱하여 커널의 중앙 노드에서$$평활값인 ${\displaystyle {\mathrm{다항}}_{}}$ 계수 $a{\displaystyle {}_{}}$ 00{\$displaystyle a_{00$를 얻을 수 있는 35개의 콘볼루션 계수가 포함되어 있다(위 표의 18번째 노드에서).마찬가지로 C의 다른 행에 35개의 값을 곱하여 다른 다항식 계수를 얻을 수 있으며, 이 계수를 사용하여 다른 노드에서 평활값과 다른 평활 부분파생상품을 구할 수 있다.

니키타스와 파파 루이지는 사용된 다항식의 형식에 따라 스무딩의 품질이 크게 달라질 수 있다는 것을 보여주었다.^[19]그들은 양식의 다항식 사용을 권장한다.

${\displaystyle Y=\sum _{i=0}^{p}\sum _{j=0}^{q}a_{ij}v^{i}w^{j}}}}}}$

그러한 다항식은 커널의 중앙 및 근거리 영역 모두에서 양호한 평활화를 달성할 수 있으므로 샘플링된 도메인의 내부 및 근거리 데이터 지점 모두에서 평활에 자신 있게 사용할 수 있다.최소 제곱 문제를 해결할 때 불협화음을 방지하기 위해 p < m과 q < n. 2차원 계수를 계산하는 소프트웨어와 그러한 C의 데이터베이스에 대해서는 아래 다차원 콘볼루션 계수에 대한 섹션을 참조하십시오.

다차원 콘볼루션 계수

2차원 콘볼루션 계수의 아이디어는 커널 노드의 다차원 분포를 한 줄로 배열함으로써 보다 높은 공간 차원에서도 쉽게 확장할 수 있다.^[16][20]니키타스와 파파 루이지가^[19] 2차원 사례에서 앞서 발견한 것에 이어 다차원 사례에서는 다음과 같은 형태의 다항식 사용을 권장한다.

${\displaystyle Y=\sum _{i_{1}=0}^{p_{1}}\sum _{2}=0}^{p_{2}}\cdots \sum \sum _{i_{i_{{}}}}}}D}=0}^{p_{D}}(a_{i_{1}i_{2}}\cdots i_{{D}\time u_{1}^{{1}i_{1}u_{2}^{D}^{D}^{D}^{D}}}}}}}}}}}}$

여기서 D는 공간의 치수, ${\displaystyle a$$s$는 다항 계수, u는 서로 다른 공간 방향의 좌표다.혼합이든 아니든 모든 순서의 부분파생물에 대한 대수적 표현은 위의 표현에서 쉽게 파생될 수 있다.^[20]참고로 C는 커널 노드가 일렬로 배열되는 방식과 제이코비안을 준비할 때 위의 확장된 형태의 서로 다른 용어들이 배열되는 방식에 따라 달라진다.

컴퓨터 프로그래밍 언어로 사용할 수 있는 표준 부동 소수점 숫자의 정밀도가 더 이상 충분하지 않기 때문에 다차원 사례에서 C의 정확한 계산이 어려워진다.정밀도가 부족하면 부동소수점 절단 오차가 일부 C요소의 크기에 비견될 수 있으며, 이는 다시 그 정확도를 심각하게 떨어뜨려 무용지물로 만든다.Chandra Shekhar는 이러한 정확성 문제를 적절하게 처리하는 두 가지 오픈 소스 소프트인 ACCC(Advanced Convolution Coefficulator Calculator)와 PCCCC(정밀 콘볼루션 계수 계산기)를 내놓았다.ACCC는 부동 소수점 번호를 반복적으로 사용하여 계산을 수행한다.^[21]부동 소수점 숫자의 정밀도는 GNU MPR을 사용하여 각 반복에서 점진적으로 증가한다.두 번 연속적으로 획득한 C가 사전 지정된 거리까지 동일한 유의 자릿수를 가지기 시작하면 수렴이 도달한 것으로 가정한다.거리가 충분히 큰 경우, 계산은 매우 정확한 C를 산출한다. PCCC는 GNU Multiple Precision Mathing Library를 사용하여 합리적인 수 계산을 채택하고, 합리적인 수 형식에서 완전히 정확한 C를 산출한다.^[22]결국, 이러한 합리적인 숫자는 미리 지정된 숫자의 유의한 숫자가 될 때까지 부동 소수점 숫자로 변환된다.

대칭 커널과 대칭 및 비대칭 다항식, 유니티 스페이스 커널 노드, 1, 2, 3, 4차원 공간에서 ACCC를 사용하여 계산한 C의 데이터베이스를 사용할 수 있다.^[23]Chandra Shekhar는 또한 앞서 언급한 데이터베이스에 제공된 C의 사용을 허용하면서 ^[20]균일하지 않은 간격의 커널 노드에 대해 필터링과 부분적인 차이(다양한 주문의)를 수행하기 위해 유니티 스페이스 커널 노드에 대해 계산된 C의 사용을 기술하는 수학적 프레임워크를 내놓았다.이 방법은 대략적인 결과만 산출하지만 커널 노드의 불균일성이 약하다는 전제하에 대부분의 엔지니어링 애플리케이션에서 허용된다.

콘볼루션의 일부 특성

1. 평활화를 위한 콘볼루션 계수의 합은 1과 같다.홀수 유도체의 계수 합계는 0이다.^[24]
2. 평활화를 위한 제곱된 콘볼루션 계수의 합은 중심 계수의 값과 동일하다.^[25]
3. 함수의 평활은 함수의 아래 영역을 변경하지 않는다.^[24]
4. 균등파생 계수를 갖는 대칭함수의 경련은 대칭의 중심을 보존한다.^[24]
5. 파생 필터의 속성.^[26]

신호 왜곡 및 소음 감소

콘볼루션 과정에서 신호가 왜곡될 수밖에 없다.위의 속성 3부터, 피크가 있는 데이터를 평활화하면 피크의 높이가 낮아지고 반폭은 커진다.왜곡과 신호 대 잡음 비(Signal-to-Noise ratio) 개선의 범위:

• 다항식의 정도가 증가함에 따라 감소하다.
• convolution 함수의 폭, m이 증가함에 따라 증가한다.

예를 들어 모든 데이터 포인트의 노이즈가 상관관계가 없고 일정한 표준 편차인 σ을 갖는 경우, 다음과 같은^{[25][note 5]} m 포인트 스무딩 기능을 가진 콘볼루션에 의해 노이즈의 표준 편차가 감소한다.

다항식 도 0 또는 1: ${\displaystyle \sqrt{\frac{\mathrm{1m}}{}}}$ ${\displaystyle \sqrt{\sigma }}$ ${\displaystyle {\sqrt {$1$\over$ m$}\ma }($이동 평균)

다항식도 2 또는 3:$3{\displaystyle \sqrt{\frac{\mathrm{}}{}}}$(${\displaystyle \sqrt{\frac{{3m\mathrm{}}^{}}{}}}$ 2${\displaystyle \sqrt{\frac{{}^{}}{}}}$- 7${\displaystyle \sqrt{\frac{}{}}}$) ${\displaystyle \sqrt{\frac{\mathrm{4m}}{}}}$(${\displaystyle \sqrt{\frac{{m\mathrm{}}^{}}{}}}$ 2${\displaystyle \sqrt{\frac{{}^{}}{}}}$- ${\displaystyle \sqrt{\frac{4}{}}}$) ${\displaystyle \sqrt{\frac{}{}}}$ ${\displaystyle {\sqrt$ {\$sqrt {\3m^{2}-7)}{4m(m^{2}-4)}\\ma$ $\}\}.$

이러한 함수는 오른쪽 그림에서 볼 수 있다.예를 들어 9점 선형 함수(이동 평균)를 사용하면 노이즈의 3분의 2가 제거되고 9점 2차/큐빅 스무딩 함수를 사용하면 노이즈의 약 절반만 제거된다.나머지 소음의 대부분은 저주파 소음이다(아래 콘볼루션 필터의 주파수 특성 참조).

이동 평균 함수는 최상의 노이즈 감소를 제공하지만 m 지점에 대한 곡면성이 있는 데이터를 평활하기에 적합하지 않다.2차 필터 함수는 2차 다항식이 없기 때문에 변곡점이 있는 데이터 곡선의 파생 모델을 얻는 데 적합하지 않다.다항식 순서와 콘볼루션 계수의 최적 선택은 소음 감소와 왜곡 사이의 절충이 될 것이다.^[27]

멀티패스 필터

왜곡을 완화하고 노이즈 제거를 개선하는 한 가지 방법은 폭이 더 작은 필터를 사용하여 두 개 이상의 콘볼루션을 수행하는 것이다.동일한 필터의 두 패스에 대해 이것은 원래 필터 자체와의 콘볼루션으로 얻은 필터의 한 패스에 해당한다.^[28]예를 들어 계수가 있는 필터(1/3, 1/3, 1/3)의 패스는 계수(1/9, 2/9, 3/9, 2/9, 2/9, 1/9)가 있는 필터의 패스를 1회 패스하는 것과 같다.

다중 할당 시 단점은 $m{\displaystyle }$ ${\displaystyle m}$– 포인트 함수의 n ${\displaystyle n}$ 통과에$$ 해당하는 필터 너비가 n${\displaystyle (m}$- ${\displaystyle 1}$)${\displaystyle }$+ $(\displaystyle n(m-1)+1}$이므로 다중 할당 시 엔드 효과가 더 크다는 것이다.그럼에도 불구하고, 멀티캐스팅은 큰 이점을 위해 사용되어 왔다.예를 들어, 신호 대 잡음 비율이 5에 불과한 일부 40 대 80의 데이터는 유용한 결과를 제공했다.^[29]위에 제시된 소음 감소 공식은 각 통과에 따라 계산된 데이터 지점 간의 상관관계가 증가하기 때문에 적용되지 않는다.

콘볼루션 필터의 주파수 특성

콘볼루션은 푸리에 공동 도메인의 곱셈에 매핑된다.콘볼루션 필터의 이산 푸리에 변환은 실제 값 함수로서 다음과 같이 나타낼 수 있다.

${\displaystyle FT(\theta )=\sum _{j={\tfrac {1-m}{2}}^{\tfrac {m-1}{2}}C_{j}\cos(j\teta )}}$

θ은 0도에서 180도까지 진행되며, 그 후에는 함수가 저절로 반복된다.9점 이차/큐빅 스무딩 함수에 대한 그래프가 대표적이다.매우 낮은 각도에서 그래프는 거의 평평하며, 이는 데이터의 저주파 성분이 평활 연산에 의해 사실상 변경되지 않는다는 것을 의미한다.각도가 증가하면 값이 감소하여 주파수 성분이 점점 더 감쇠된다.이는 콘볼루션 필터를 저역 통과 필터로 설명할 수 있음을 보여준다: 제거되는 노이즈는 주로 고주파 노이즈이며 저주파 노이즈는 필터를 통과한다.^[30]일부 고주파 노이즈 구성 요소는 푸리에 변환에서 큰 각도로 분해된 것에서 알 수 있듯이 다른 구성 요소보다 더 감쇠된다.이것은 평활된 데이터에 작은 진동을 일으킬 수 있다.^[31]

콘볼루션 및 상관 관계

콘볼루션은 데이터 오류 간의 상관관계에 영향을 미친다.콘볼루션의 효과는 선형 변환으로 표현될 수 있다.

${\displaystyle Y_{j}\ =\sum _{i=-{\frac {m-1}{2}}^{\frac {m-1}{2}}C_{i}\,y_{j+i}}}}}$

오차 전파 법칙에 의해 데이터의 분산-공분산 행렬 A는 다음과 같이 B로 변환된다.

${\displaystyle \mathbf {B} =\mathbf {C} \mathbf {A} \mathbf {C}^{T}}$

이 점이 실제로 어떻게 적용되는지 확인하려면 데이터 점이 분산이 같고 서로 상관 관계가 없다고 가정하여 처음 세 개의 계산된 점인 Y₂ - Y에₄ 대한 3점 이동 평균의 효과를 고려하십시오.A는 식별 행렬에 각 점에서의 상수, σ², 분산을 곱한 것이 된다.

${\displaystyle \mathbf{B}={\sigma ^{2}\over 9}{\begin{pmatrix}1&, 1&, 1&, 0&, 0\\0&, 1&, 1&, 1&, 0\\0&, 0&, 1&, 1&, 1\end{pmatrix}}{\begin{pmatrix}1&, 0&, 0&, 0&, 0\\0&, 1&, 0&, 0&, 0\\0&, 0&, 1&, 0&, 0\\0&, 0&, 0&, 1&, 0\\0&, 0&, 0&, 0&, 1\end{pmatrix}}{\begin{pmatrix}1&, 0&0.\\1&, 1&, 0\\1&, 1&, 1\\0&, 1&, 1\\0&, 0&, 1\end{pmatrix}}={\sigma ^{2}\over 9}{\begin{pmatrix}3&, 2&, 1\\2&, 3&, 2\\1&, 2&, 3\end{pmatrix}}}$

이 경우 상관 계수는

${\displaystyle \rho_{ij}={\frac {B_{ij}}{\sqrt{B_{j}}},\(i\neq j)}}$

계산된 포인트 사이에 i와 j가 될 것이다.

${\displaystyle \rho _{i,i+1}={2 \over 3}=0.66,\,\rho_{i,i+2}={1 \over 3}=0.33}$

일반적으로 계산된 값은 관측된 값이 상관관계가 없는 경우에도 상관관계가 있다.상관관계는 한 번에 m - 1로 계산된다.^[32]

멀티패스 필터

데이터 집합의 노이즈 및 상관 관계에 대한 다중 할당 효과를 설명하려면 3점 이동 평균 필터의 두 번째 통과 효과를 고려하십시오.두 번째 패스용^{[note 6]}

${\displaystyle \mathbf {CBC^{T}}={\sigma ^{2}\over 81}{\begin{pmatrix}1&, 1&, 1&, 0&, 0\\0&, 1&, 1&, 1&, 0\\0&, 0&, 1&, 1&, 1\end{pmatrix}}{\begin{pmatrix}3&, 2&, 1&, 0&, 0\\2&, 3&, 2&, 0&, 0\\1&, 2&, 3&, 0&, 0\\0&, 0&, 0&, 0&, 0\\0&, 0&, 0&, 0&, 0\end{pmatrix}}{\begin{pmatrix}1&, 0&, 0\\1&, 1&, 0\\1&am.p/&1&, 1\\0&, 1&, 1\\0&, 0&, 1\end{pmatrix}}={\sigma ^{2}\over 81}{\begin{pmatrix}19&, 16&, 10&, 4&, 1\\16&, 19&, 16&, 10&, 4\\10&, 16&, 19&, 16&, 10\\4&, 10&, 16&, 19&, 16\\1&, 4&, 10&, 16&, 19\end{pmatrix}}$

두 번의 통과 후 중앙점의 표준 편차는 한 번의 통과에 대해 0.58σ에 비해 ${\displaystyle \sqrt{\frac{19}{}}}$ ${\displaystyle \sqrt{81\sigma }}$= ${\displaystyle 0.\mathrm{48\sigma }}$ ${\displaystyle {\sqrt{19}{81}}}\sigma =$ 0.$48\sigma }}$로 줄었다$.$소음 감소는 동일한 조건에서 평활된 지점이 0.45㎛의 더 작은 표준 편차를 갖는 5점 이동 평균의 1회 통과보다 약간 낮다.

상관 계수가 있는 4개의 순차적 점 범위에 걸쳐 상관 관계가 확장됨

${\displaystyle \rho_{i,i+1}={16 \over 19}=0.84,\rho_{10 \over 19}=0.53,\rho_{4 \over 19}=0.21,\rho_{i,i+4}={1 \19}=0.05}$

보다 좁은 평활 기능으로 두 번의 패스를 수행하여 얻은 이점은 계산된 데이터에 왜곡이 적다는 것이다.

참고 항목

• 커널 매끄러움 – 통계에 사용되는 많은 동일한 프로세스에 대해 서로 다른 용어
• 로컬 회귀 분석 - LOESS 및 LOWESS 방법
• 수치적 차별화 – 기능의 차별화에 대한 적용
• 스무딩 스플라인
• 스텐실(숫자 분석) – 미분방정식의 용액 적용

부록

선택한 콘볼루션 계수 표

데이터 포인트 세트$({\displaystyle {}_{}}$ ${\displaystyle j_{}}$, ${\displaystyle {}_{}}$ ${\displaystyle j_{}{}_{}}$) ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {\le }_{}}$ ${\displaystyle j_{}}$ ${\displaystyle {\le }_{}}$ ${\displaystyle n_{}}$ ${\$ n$}}$을 고려하십시오$.$사비츠키-골레이 표는 $step{\displaystyle {}_{}}$ x${\displaystyle {}_{}{}_{}}$ - ${\displaystyle x_{}}$ j${\displaystyle {}_{}}$- ${\displaystyle 1_{}}$ ${\$}-x_${j-1}$ step x - x는$$ h. 입방 다항식과 창 크기 m, m, 5점인 이른바 콘볼루션 계수의 사용 예는 다음과 같다.

스무딩

${\displaystyle Y_{j}={\frac {1}{35}}(-3\times y_{j-2}+12\times y_{j-1}+17\times y_{j}+12\times y_{j+1}-3\times y_{j+2})}$ ;

제1차 파생상품

${\displaystyle Y'_{j}={\frac {1}{12h}}(1\times y_{j-2}-8\times y_{j-1}+0\times y_{j}+8\times y_{j+1}-1\times y_{j+2})}$ ;

제2차 파생상품

${\displaystyle Y''_{j}={\frac {1}{7h^{2}}}(2\times y_{j-2}-1\times y_{j-1}-2\times y_{j}-1\times y_{j+1}+2\times y_{j+2})}$.

도 1, 2, 3, 4, 5의 다항식에 대한 콘볼루션 계수의 선택된 값은 다음 표에^{[note 7]} 제시되어 있다. 이 값은 Gorry에서 제공된 PASCAL 코드를 사용하여 계산되었다.^[15]

평활화 계수 다항식 정도 이차 또는 입방체 둘 또는 셋 4중주 또는 5중주 4시나 창 크기 5 7 9 7 9 −4 −21 15 −3 −2 14 5 −55 −2 −3 3 39 −30 30 −1 12 6 54 75 135 0 17 7 59 131 179 1 12 6 54 75 135 2 −3 3 39 −30 30 3 −2 14 5 −55 4 −21 15 정상화 35 21 231 231 429

첫 번째 파생상품 계수 다항식 정도 선형 또는 이차적 하나 또는 둘 입방 또는 사방형의 서너 개 창 크기 3 5 7 9 5 7 9 −4 −4 86 −3 −3 −3 22 −142 −2 −2 −2 −2 1 −67 −193 −1 -1 −1 −1 −1 −8 −58 −126 0 0 0 0 0 0 0 0 1 1 1 1 1 8 58 126 2 2 2 2 −1 67 193 3 3 3 −22 142 4 4 −86 정상화 2 10 28 60 12 252 1,188

2차 파생상품 계수 다항식 정도 이차 또는 입방체 둘 또는 셋 4중주 또는 5중주 4시나 창 크기 5 7 9 5 7 9 −4 28 −126 −3 5 7 −13 371 −2 2 0 −8 −1 67 151 −1 −1 −3 −17 16 −19 −211 0 −2 −4 −20 −30 −70 −370 1 −1 −3 −17 16 −19 −211 2 2 0 −8 −1 67 151 3 5 7 −13 371 4 28 −126 정상화 7 42 462 12 132 1716

제3차 파생상품 계수 다항식 정도 입방 또는 사방형의 서너 개 5진법 또는 6진법 대여섯 창 크기 5 7 9 7 9 −4 −14 100 −3 −1 7 1 −457 −2 −1 1 13 −8 256 −1 2 1 9 13 459 0 0 0 0 0 0 1 −2 −1 −9 −13 −459 2 1 −1 −13 8 −256 3 1 −7 −1 457 4 14 −100 정상화 2 6 198 8 1144

제4차 파생상품 계수 다항식 정도 4중주 또는 5중주 4시나 창 크기 7 9 −4 14 −3 3 −21 −2 −7 −11 −1 1 9 0 6 18 1 1 9 2 -7 −11 3 3 −21 4 14 정상화 11 143

메모들

참조

• Gans, Peter (1992). Data fitting in the chemical sciences: By the method of least squares. ISBN 9780471934127.

외부 링크

위키미디어 커먼즈에는 사비츠키-골레이 필터와 관련된 미디어가 있다.

• 다차원 최소 제곱 필터용 ACC(고급 콘볼루션 계수 계산기)
• Savitzky-Golay 필터 - 통계 기초
• 중심점으로부터의 데이터 세트 크기, 적합 순서 및 오프셋의 범위에 대한 광범위한 계수