나사(단순 기계)

나사는 회전 운동을 선형 운동으로, 토크(회전력)^[1]를 선형 힘으로 변환하는 메커니즘입니다.그것은 6개의 고전적인 단순한 기계 중 하나이다.가장 일반적인 형태는 원통형 샤프트로 구성되어 있으며,^[2][3] 외부에는 나사산이라고 불리는 나선형 홈이나 능선이 있습니다.나사는 다른 물체 또는 매체의 구멍을 통과하며 구멍 안쪽에 나사산이 나사의 나사산과 맞물립니다.나사 축이 고정 나사산을 기준으로 회전하면 나사는 나사축을 둘러싼 매체에 대해 축을 따라 이동합니다. 예를 들어, 목재 나사를 회전시키면 나사가 나사축을 강제로 나무로 만듭니다.나사기구는 나사축이 고정물체의 나사구멍을 통해 회전하거나 너트 등의 나사칼라가 고정물축 ^[4][5]주위를 회전할 수 있다.기하학적으로 볼 때 ^[1]나사는 실린더를 감싼 좁은 경사면으로 볼 수 있다.

다른 단순한 기계와 마찬가지로 나사는 힘을 증폭시킬 수 있습니다. 샤프트의 작은 회전력(토크)은 부하에 큰 축력을 가할 수 있습니다.피치(나사 나사산 사이의 거리)가 작을수록 기계적 이점(입력력에 대한 출력 비율)이 커집니다.나사는 물체를 고정하기 위한 나사 고정 장치와 용기, 가시, 나사 잭, 나사 프레스 등의 장치에 널리 사용됩니다.

같은 원리를 사용하는 다른 메커니즘(나사라고도 함)은 샤프트나 나사산이 반드시 있는 것은 아닙니다.예를 들어, 코르크따개는 뾰족한 끝이 있는 나선형 막대이고, 아르키메데스의 나사는 물을 위로 이동시키기 위해 회전하는 나선형 챔버를 사용하는 워터 펌프입니다.모든 나사의 공통 원리는 회전하는 나선은 선형 운동을 일으킬 수 있다는 것입니다.

역사

나사는 ^[6]발명된 마지막 간단한 기계 중 하나였다.그것은 기원전 ^[7]911-609년에 메소포타미아에서 처음 나타났고, 이후 고대 이집트와 고대 ^[8][9]그리스에서 나타났다.

기록에 따르면 물나사, 즉 나사 펌프가 ^[10][11]고대 이집트에서 처음 사용되었고,^[12] 그리스 철학자 아르키메데스가 기원전 234년경에 아르키메데스의 나사식 물 펌프를 묘사하기 전입니다.아르키메데스는 나사에 대한 최초의 이론적 연구를 ^[13]기계로 썼고 고대 그리스에서 ^[9][14]나사를 도입한 것으로 여겨진다.기원전 1세기까지, 나사는 나사 압착기와 아르키메데스의 ^[10]나사의 형태로 사용되었다.

그리스 철학자들은 나사를 단순한 기계들 중 하나로 정의했고 그 (이상적인) 기계적 ^[15]이점을 계산할 수 있었다.예를 들어 알렉산드리아의 Heron(52 AD)은 나사를 "하중을 이동시킬 수 있는" 5가지 메커니즘 중 하나로 나열하고 실린더를 감싸는 경사면으로 정의하며 나사산을 ^[17]절단하는 탭을 포함하여 나사산의 제작 및 용도를 ^[16]설명했습니다.

복잡한 나선형 모양은 손으로 힘겹게 잘라야 했기 때문에 고대에는 나사가 일부 기계에서만 연결로 사용되었습니다.나사 고정 장치는 나사 절단 선반이 ^[18]개발된 후 15세기에야 시계에서 사용되기 시작했습니다.이 나사는 유럽 ^[12]회화에 오거와 드릴의 이미지가 나타나기 시작한 이 무렵에 (물 외에) 구멍을 뚫고 움직이는 재료에도 적용되었던 것으로 보인다.나사를 포함한 단순한 기계의 완전한 동적 이론은 1600년 이탈리아 과학자 갈릴레오 갈릴레이가 르 메카니헤에서 고안했습니다.^{[9]: 163 [19]}

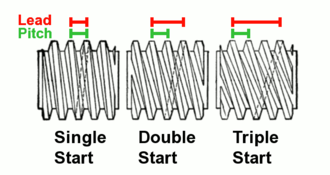
리드 앤 피치

나사산의 미세도 또는 거칠기는 밀접하게 관련된 두 가지 ^[5]양으로 정의됩니다.

• 리드는 나사가 1회전(360°)으로 이동하는 축 거리(나사의 축과 평행)로 정의됩니다.수갱의.리드선은 나사의 기계적 이점을 결정합니다. 리드선이 작을수록 기계적 이점이 ^[20]높아집니다.
• 피치는 인접한 나사산의 볏 사이의 축 거리로 정의됩니다.

"싱글 스타트" 나사라고 불리는 나사에는 단일 나선형 나사산이 감겨 있어 리드선과 피치가 동일합니다.여러 개의 나사산이 서로 얽혀 있는 "다중 시동" 나사가 다를 뿐입니다.이 나사에서 리드는 피치에 출발 횟수를 곱한 값과 같다.다중 시작 나사는 병의 나사 캡 및 볼 포인트 펜 등 특정 회전에 대해 큰 선형 모션이 필요할 때 사용됩니다.

손재주

나사산의 나선은 두 가지 방향으로 꼬일 수 있는데, 이를 핸드니스라고 합니다.대부분의 나사산은 위에서 보았을 때 시계 방향으로 ^[21][22]돌렸을 때 나사축이 뷰어에서 멀어지도록 방향을 잡습니다(나사가 조여집니다).오른손의 손가락을 회전 방향으로 축 주위에 구부리면 엄지손가락이 축의 운동 방향을 가리킨다는 오른손 그립 규칙을 따르기 때문에 오른손(RH) 나사산이라고 합니다.반대 방향으로 향하는 나사산을 LH(왼손잡이(LH)

일반적으로 오른손잡이는 나사산의 ^[21]기본 핸들링입니다.따라서 대부분의 나사산 부품 및 고정 장치에는 우측 나사산이 있습니다.왜 오른손잡이 나사산이 표준이 되었는지에 대한 한 가지 설명은 오른손잡이 드라이버로 오른손잡이 나사를 조이는 것이 왼손잡이 나사를 조이는 것보다 쉽다는 것이다. 왜냐하면 그것은 약한 회전자 ^[21]근육보다 강한 반향자 근육을 사용하기 때문이다.대부분의 사람들이 오른손잡이이기 때문에 나사 고정 장치에서는 오른손잡이 나사산이 표준이 되었습니다.

기계의 나사 연결은 예외이며, 어느 쪽이 더 적합한지에 따라 오른손잡이 또는 왼손잡이일 수 있습니다.왼쪽 나사산은 일부 다른 용도에도 사용됩니다.

• 샤프트의 회전으로 인해 기존의 오른손 너트가 플렛팅 유도 세차 때문에 조이지 않고 느슨해지는 경우.예를 들어 다음과 같습니다.
  • 자전거의 ^[21][23]왼쪽 페달.
  • 원형 톱날 또는 벤치 그라인더 휠을 고정하는 왼쪽 나사.
• 턴버클이나 탈착식 파이프 세그먼트와 같이 양 끝에 나사산이 있는 일부 장치에서는이 부품에는 오른손용 나사산과 왼손용 나사산이 각각 1개씩 달려 있어 두 나사산을 동시에 조이거나 느슨하게 합니다.
• 일부 가스 공급 연결부에서는 위험한 잘못된 연결을 방지하기 위해 사용됩니다.예를 들어 가스 용접에서는 인화성 가스 공급 라인이 왼손용 나사산으로 부착되어 있으므로 실수로 오른손용 나사산을 사용하는 산소 공급 라인과 전환되지 않습니다.
• 일반인들에게 쓸모없는 전구를 만들기 위해, 일부 기차역이나 지하철역에서는 ^[21]왼손 전구를 사용한다.
• 관 뚜껑은 전통적으로 왼손 ^[21][24][25]나사로 고정되었다고 한다.

나사산

다양한 용도로 사용되는 나사산에는 다양한 형태의 나사산이 사용됩니다.나사산은 서로 다른 제조사가 만든 부품이 올바르게 맞물릴 수 있도록 표준화되어 있습니다.

나사산 각도

나사산 각도는 나사산의 두 베어링 면 사이의 축과 평행한 섹션에서 측정된 포함 각도입니다.축방향 하중력과 베어링 표면에 대한 법선 사이의 각도는 대략 나사산의 절반 정도이므로 나사산의 마찰과 효율은 물론 마모율과 강도에도 큰 영향을 미칩니다.나사산 각도가 클수록 하중 벡터와 표면 법선 사이의 각도가 커지므로 주어진 하중을 지탱하는 데 필요한 나사산 사이의 정상 힘이 커집니다.따라서 나사산 각도를 높이면 나사의 마찰 및 마모가 증가합니다.

외측을 향한 각진 나사산 베어링 표면은 하중력에 의해 작용될 때 너트에 반경 방향(외측)의 힘을 가하여 인장 응력을 유발합니다.이 방사형 폭발력은 나사산 각도가 증가함에 따라 증가합니다.너트 재료의 인장 강도가 부족할 경우 나사 각도가 큰 너트에 과도한 하중이 가해지면 너트가 갈라질 수 있다.

나사산의 각도는 나사산의 강도에도 영향을 미칩니다.각도가 큰 나사산은 크기에 비해 뿌리가 넓고 강합니다.

스레드 종류

나사형 고정 장치의 경우, ^[5]고정 장치가 풀리지 않도록 하기 위해 많은 마찰이 허용되며 일반적으로 필요합니다.따라서 고정 장치에 사용되는 나사산은 일반적으로 60°의 나사산 각도를 가집니다.

• (a) V 나사산
  주요 기사:셀프 태핑 나사
  - 나무 나사, 판금 나사 등 날카로운 날이 필요한 자체 태핑 나사, 고정 나사, 조정 나사 등 나사를 움직이지 않도록 하기 위해 추가적인 마찰이 필요한 경우, 나사산 파이프 이음매처럼 조인트가 유체가 단단해야 하는 경우에 사용합니다.
• (b) 미국 국적
  상세 정보:국가 파이프 나사산
  - 거의 동일한 Unified Thread Standard로 대체되었습니다.V 나사산과 60° 나사 각도가 동일하지만 루트가 평평하기 때문에 더 강합니다.볼트, 너트 및 다양한 고정 장치에 사용됩니다.
• 다. 미터법 나사산
  주요 기사:메트릭 스레드
  - 이러한 스레드는 ISO 및 DIN 표준에 따라 지정되며 공통적입니다.
• (d) Whitworth 또는 영국 표준
  주요 기사: British Standard Whitworth
  - Unified Thread Standard로 대체된 영국 표준과 매우 유사합니다.

반면 리드 나사 또는 잭 나사 등의 기계 연결에서는 마찰이 ^[5]최소화되어야 합니다.따라서 각도가 작은 나사산이 사용됩니다.

• 마 정사각형 나사산
  주요 기사: 정사각형 나사산
  - 나사산 각도가 ^[5]0°인 가장 강하고 가장 낮은 마찰 나사산으로 너트에 폭발력을 가하지 않습니다.그러나 제작이 어려우며,^[5] 모서리를 언더컷해야 하므로 단일 점 절단 공구가 필요합니다.잭 나사 및 리드 나사 등 고부하 용도에 사용되지만 대부분 Acme 스레드로 대체되었습니다.대신 5° 나사 각도가 작은 변형된 정사각형 나사산이 사용되기도 하는데, 이는 제조 비용이 저렴합니다.
• 바 Acme 나사
  주요 기사:Acme 스레드
  - 나사 각도가 28°이므로 정사각형 나사산에 비해 마찰력이 높지만 제작이 용이하며 마모 ^[5]조정 시 분할 너트와 함께 사용할 수 있습니다.이는 선반과 같은 기계의 가시, C-클램프, 밸브, 가위 잭 및 리드 나사에 널리 사용됩니다.
• 사 버트리스 나사
  주요 기사:버트리스 나사산
  - 나사 잭과 같이 ^[5]한 방향으로만 하중이 가해지는 고부하 용도에 사용됩니다.베어링 표면의 각도가 0°이므로 정사각형 나사산만큼 효율적이지만 더 강하고 제작이 쉽습니다.
• (h) 너클 나사
  주요 기사: 너클 나사산
  - 모서리를 둥글게 하여 파손을 방지하고 마찰력을 높인 정사각형 실과 유사합니다.저강도 용도에서는 압연 방식으로 시트 스톡에서 저렴하게 제조할 수 있습니다.전구와 소켓에 사용됩니다.

사용하다

• 나사는 자체 잠금 특성(아래 참조)으로 인해 목재 나사, 판금 나사, 스터드 및 볼트와 너트 등 물체 또는 재료를 함께 고정하는 나사 고정 장치에 널리 사용됩니다.
• 또한 자체 잠금 특성은 코르크 나사, 나사 상단 용기 뚜껑, 나사산 파이프 조인트, 바이스, C-클램프 및 나사 잭과 같은 다양한 다른 용도로 나사를 사용하는 데에도 중요합니다.
• 나사는 기계, 웜 기어, 리드 나사, 볼 나사 및 롤러 나사에서도 동력을 전달하기 위한 연결로 사용됩니다.나사 링크는 효율성이 낮기 때문에 고출력을 전달하는 데 거의 사용되지 않지만 액추에이터 위치 결정과 같은 저출력의 간헐적 사용에 더 많이 사용됩니다.
• 회전하는 나선형 나사 블레이드 또는 챔버는 아르키메데스의 나사, 오거 접지 드릴 및 나사 컨베이어의 재료를 이동하는 데 사용됩니다.
• 마이크로미터는 정밀 보정된 나사를 사용하여 길이를 매우 정확하게 측정합니다.

나사 프로펠러는 나사라는 이름을 공유하지만 위의 나사 유형과는 매우 다른 물리적 원리로 작동하므로 이 문서의 정보는 해당되지 않습니다.

이동 거리

α$${\$displaystyle \alpha}$의 각도로 회전할 때 나사 샤프트가 이동하는 선형 $거리{\displaystyle }$d {\$displaystyle$ d$}$는 다음과 같습니다.

${{displaystyle d=llcfrac}{360^{\display }},$

여기서 l$\$ l은$$나사의$$ 리드입니다.

단순 기계의 거리 비율은 가해진 힘이 하중이 이동하는 거리에 대한 거리의 비율로 정의됩니다.나사의 경우 샤프트 가장자리에 있는 점이 샤프트가 움직이는 선형 거리에_out 대한_in 원형 거리 d의 비율입니다.r이 축의 반지름인 경우 나사 림의 한 점이 2µr의 거리를 이동하는 반면 축은 리드 거리 l만큼 직선적으로 움직입니다.그래서 거리비는

${{displaystyle {mbox {distance ratio}}\equiv {frac {d_{in}} {d_{out}}=blac {2\pi r} {l}},$

마찰이 없는 기계적 이점

나사의 기계적 이점 MA는 하중을 가할 때 샤프트가 가하는 축방향 출력력_out F와 샤프트의 림에 가해지는 회전력_in F의 비율로 정의됩니다.마찰이 없는 나사(이상적 나사라고도 함)의 경우, 에너지 보존에 의한 입력력에 의한 나사에서의 작업은 하중력에 대한 나사에 의한 작업과 동일합니다.

${\displaystyle W_{in}=W_{out},}$

작업은 작용하는 거리에 힘을 곱한 것과 같으므로 나사를 한 바퀴 완전히 돌리면 ${\displaystyle {\mathrm{Win}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 2}$ ${\displaystyle \mu }$ r ${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{in}}_{}{}_{}}${$display style$ W_${in$} = $2\pi$ rF_${in$$},$ 부하에$$ 대한 $작업$은 ${\displaystyle W_{}}$ ${\displaystyle o_{}}$ t ${\displaystyle {}_{}}$ $L$ F ${\displaystyle {}_{}}$ t${\displaystyle {}_{}}{\displaystyle u_{}}$ {$display style$ W_out}입니다.l 거리 비율:

나사의 기계적 이점은 $리드선{\displaystyle }$ l{$displaystyle$ l$\}$에 따라 결정되며 나사산 사이의 거리가 작을수록 기계적 이점이 커지며 나사가 주어진 힘을 가할 때 가할 수 있는 힘이 커집니다$.$그러나 대부분의 실제 나사는 마찰력이 크고 기계적 이점도 위의 방정식보다 낮습니다.

토크 형태

나사에 가해지는 회전력은 $실제로{\displaystyle {}_{}}$ 토크 ${\displaystyle {\mathrm{Ti}}_{}}$ n $=$ ${\displaystyle {}_{}}$ n$$r (\$displaystyle T_${in$}=F_{in}$r$,\})$입니다.따라서 나사를 돌리는 데 필요한 입력력은 샤프트에서 얼마나 떨어져 있는가에 따라 달라집니다.나사에 가해지는 힘은 일반적으로 위에서 가정한 바와 같이 림에 적용되지 않습니다.예를 들어 볼트는 렌치가 레버 역할을 하는 등 어떤 형태의 레버에 의해 사용되는 경우가 많습니다.이 경우의 기계적 이점은 위의 방정식의 r에 대한 레버 암의 길이를 사용하여 계산할 수 있습니다.이 외부 요인 r은 위의 방정식에서 토크 측면에서 이 요소를 제거할 수 있습니다.

${\displaystyle {F_{out}}{T_{in}}=blac {2\pi }{l}},$

실제 기계적 우위성과 효율성

이동 나사산과 고정 나사산 사이의 슬라이딩 접촉 면적이 넓기 때문에 일반적으로 나사는 마찰 에너지 손실이 큽니다.윤활이 잘 된 잭 나사도 효율이 15%~20%에 불과하고, 회전 시 가해지는 나머지 작업도 마찰에 의해 손실됩니다.마찰이 포함되면 기계적 이점은 더 이상 거리 비율과 동일하지 않을 뿐만 아니라 나사의 효율에도 좌우됩니다.에너지 절약에 의해 입력력이 회전함으로써 스크루에 가해지는 워크_in W는 부하_out W를 이동시키는 워크의 합계와 같으며 스크류 내_fric 마찰 W에 의해 열로 방산된다.

${\displaystyle W_{in}=W_{out}+W_{fric},}$

효율 θ는 0과 1 사이의 무차원 수치로, 출력 작업과 입력 작업의 비율로 정의됩니다.

$\displaystyle \eta = W_{out}/W_{in},$

${\displaystyle W_{out}=\eta W_{in},}$

작업은 이동 거리에 힘을 곱한 값으로 $정의$되므로 ${\displaystyle {\mathrm{Wi}}_{}}$ n ${\displaystyle {}_{}}$ ${\displaystyle F_{}}$ ${\displaystyle {}_{}{}_{}}$ n ${\displaystyle {\mathrm{di}}_{}{}_{}}$n { $display style$ W_${in$ } ${\displaystyle {}_{}}$ $F\_{\displaystyle {}_{}}$${in} d_{$in},} ${\displaystyle {및}_{}}$ W ${\displaystyle o_{}}$ ${\displaystyle {}_{}{}_{}}$ t = F ${\displaystyle o_{}}$ ${\displaystyle t_{}}$ d${\displaystyle {}_{}}{\displaystyle o_{}}$ t { $display W_${$out$} $=$$F_{out}d_{out},}$ 이므로$$

${\displaystyle F_{out}d_{out}=\eta F_{in}d_{in},}$

${\displaystyle {F_{out}}{F_{in}}=\eta {frac {d_{in}} {d_{out}},}$

또는 토크 측면에서

${\displaystyle {F_{out}}{T_{in}}=blac {2\pi \eta}{l}}\qquad,}$

따라서 실제 나사의 기계적 이점은 효율에 의해 이상적인 마찰이 없는$나사$보다 $감소합니다.$$효율성$이 낮기 때문에 동력 기계 나사는 대량의 전력을 전달하기 위한 링크로 사용되는 경우가 많지 않지만, 보다 자주 사용되는 포지셔너입니다.아주 ^[5]조금

자체 잠금 속성

큰 마찰력으로 인해 실제로 사용되는 대부분의 나사는 "자기 잠금"이 되며, "비반복" 또는 "비오버홀링"이라고도 합니다.즉, 샤프트에 토크를 가하면 샤프트가 회전하지만, 샤프트에 가해지는 축방향 하중으로 인해 토크가 0인 경우에도 샤프트가 반대로 회전하지 않습니다.이는 "호출" 또는 "비잠금"인 다른 단순 기계와는 대조적이며, 이는 하중이 충분히 크면 뒤로 이동하거나 "오버홀"을 의미합니다.따라서 어느 방향으로든 기계를 사용할 수 있습니다.예를 들어, 레버에서 로드 엔드에 가해지는 힘이 너무 크면 레버가 뒤로 이동하면서 가해지는 힘을 처리합니다.대부분의 나사는 자체 잠금식으로 설계되어 있으며, 축에 토크가 없으면 남아 있는 위치에 그대로 유지됩니다.그러나 피치가 크고 윤활이 잘 되는 일부 나사 메커니즘은 자체 잠금 장치가 아니므로 오버홀이 발생합니다. 푸시 드릴과 같은 극소수만 이러한 "후방"의 의미로 나사를 사용하여 축방향 힘을 가하여 나사를 회전시킵니다.나사가 풀리는 다른 이유는 조립품 설계 및 충격, 진동, 동적 하중 등의 잘못된 외력 설계로 인해 나사산 및 맞물림/^[26]클램프 표면에서 미끄러짐이 발생합니다.

이러한 자체 잠금 특성은 목재 나사, 판금 나사, 스터드 및 볼트 등의 나사 고정 장치에 나사를 많이 사용하는 이유 중 하나입니다.고정 장치를 돌려서 고정하면 함께 고정되는 재료 또는 부품에 압축력이 가해집니다. 올바른 설계의 경우 부품의 힘이 아무리 가해져도 나사가 풀리지 않습니다.또한 이 특성은 나사 상단 용기 뚜껑, 가시, C-클램프 및 나사 잭에서 나사를 사용하는 데에도 기초가 됩니다.잭 샤프트를 돌리면 무거운 물체를 들어 올릴 수 있지만, 샤프트를 분리하면 어떤 높이까지 들어 올려도 그대로 유지됩니다.

$효율$이 50% ^[27][28][29]미만인 경우에만 나사가 자동으로 잠깁니다$.$

$\displaystyle \eta = flac {F_{out} / F_{in} {d_{in} / d_{out}} = flac {F_{out} {F_{in}}{\frac {l}{2\pi r}}< 0.50,}$

나사의 자체 잠금 여부는 궁극적으로 나사산의 피치 각도와 마찰 계수에 따라 달라집니다. 매우 잘 윤활되고 충분히 큰 피치의 저마찰 나사산이 "오버홀"될 수 있습니다.또한 클램프된 구성 요소가 완전히 움직이지 않도록 단단히 고정되어 있는지 확인해야 합니다.그렇지 않으면 나사산 또는 클램핑 표면이 미끄러질 ^[26]수 있습니다.

레퍼런스