근계

거짓말군과 거짓말대수
고전파 일반 선형 GL(n) 특수 선형 SL(n) 직교 O(n) 특수직교 SO(n) 유니터리 U(n) 특수 유니터리 SU(n) 심플렉틱 Sp(n)
단순 거짓말 그룹 고전적인 가n 나n 다n 라n 특출난 사2 바4 마6 마7 마8
기타 거짓말 그룹 원형 로렌츠 푸앵카레 등각군 미분동형 고리 유클리드의
거짓말대수 리 군-리 대수 대응 지수지도 연접표 살상형태 색인 단순 리 대수 루프 대수학 아핀 리 대수
반단순 리 대수 Dynkin 다이어그램 대뇌하목 근계 웨일군 실물 복잡화 스플릿 리 대수 콤팩트 리 대수
표상이론 거짓말그룹대표 거짓말 대수 표현 반단순 리 대수의 표현 이론 고전적인 리 군들의 표현 최고중량정리 보렐-바일-보트 정리
물리학의 거짓말군 입자물리학과 표현이론 로렌츠 군 표현 푸앵카레 그룹 표현 갈릴레이 군의 표현
사이언티스트 소푸스 리 앙리 푸앵카레 빌헬름 킬링 엘리 카르탕 헤르만 바일 클로드 체발리 하리쉬찬드라 아르망 보렐
용어집 거짓말 그룹 표
v t

수학에서 근계는 유클리드 공간에서 특정 기하학적 특성을 만족하는 벡터의 구성입니다. 이 개념은 리 군과 리 대수의 이론, 특히 반단순 리 대수의 분류 및 표현 이론에서 기본적인 것입니다. 리 군(그리고 대수 군과 같은 일부 유사체)과 리 대수는 20세기 동안 수학의 많은 부분에서 중요하게 되었기 때문에, 근계의 겉보기에 특별한 특성은 그들이 적용되는 영역의 수에 달려 있습니다. 또한 Dynkin 다이어그램에 의한 뿌리 시스템에 대한 분류 체계는 라이 이론(예: 특이점 이론)과 명백한 관련이 없는 수학의 일부에서 발생합니다. 마지막으로, 스펙트럼 그래프 이론에서와 같이 뿌리 시스템은 그 자체를 위해 중요합니다.^[1]

정의 및 예제

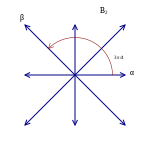
첫 번째 예로 오른쪽 이미지와 같이 2차원 유클리드 공간에 있는 6개의 벡터 R을² 고려하여 근이라고 합니다. 이 벡터는 전체 공간에 걸쳐 있습니다. 어떤 근에 수직인 선, 예를 들어 β를 생각하면, 그 선에서 R이² 반사되면 다른 근, 예를 들어 α를 다른 근으로 보냅니다. 또한 전송되는 루트는 α + nβ이며, 여기서 n은 정수입니다(이 경우 n은 1과 같습니다). 이 6개의 벡터는 다음 정의를 만족하므로 루트 시스템을 형성합니다. 이 벡터를 A라고₂ 합니다.

정의.

E를 유한 차원 유클리드 벡터 공간이라 하고, 표준 유클리드 내부 $곱$은$($⋅$,$ ⋅$)$ ${\displaystyle$ (\cdot,\cdot )}로 $표시$됩니다.$$E의 루트 $시스템$φ {\displaystyle \Phi}는 다음 조건을 만족시키는 영이 아닌 벡터(루트라고 함)의 유한 집합입니다.

1. 뿌리가 E에 걸쳐 있습니다.
2. 루트 $\alpha$ ∈ φ {\displaystyle \alpha \in \Phi}에서 {\displaystyle \Phi$}$에 속하는 유일한 스칼라 배수는 α {\displaystyle \alpha } 자체 및 - α {\displaystyle -\alpha }입니다.
3. $모든$루트 α ∈ φ {\displaystyle \alpha \in \Phi}에 대해 세트 φ set {\displaystyle \Phi}는 α {\displaystyle \alpha}에 수직인 초평면을 통해 반사 상태에서 닫힙니다.
4. (Integrality) If ${\displaystyle \alpha }$ and ${\displaystyle \beta }$ are roots in ${\displaystyle \Phi }$, then the projection of ${\displaystyle \beta }$ onto the line through ${\displaystyle \alpha }$ is an integer or half-integer multiple of ${\displaystyle \alpha }$.

조건 3과 4를 동등하게 작성하는 방법은 다음과 같습니다.

3. 임의의 두 루트 $\alpha {\displaystyle ,}$ ${\displaystyle \beta }$ ∈ φ ${\$displaystyle$$\alpha$,\$beta \in \Phi}에 대해 세트 φ {\displaystyle \Phi }에는 요소 σ α(β):= β - 2(α, β)(α, α) α가 포함됩니다. {\displaystyle \sigma _{\alpha }(\beta):=\beta -2{\frac {(\alpha,\beta)}{(\alpha,\alpha )}}}\alpha .}
4. 임의의 두 근 $\alpha {\displaystyle ,}$ ${\displaystyle \beta }$ ∈ φ ${\displaystyle \alpha$,\beta \Phi}의 경우, 숫자 ⟨ β, α ⟩ := 2 (α, β) (α, α) {\displaystyle \lang,\alpha \rangle := 2{\frac {(\alpha,\beta)}{(\alpha,\alpha)}}는 정수입니다.

일부 저자는 루트 시스템의 정의에 조건 1~3만 포함합니다.^[4] 이러한 맥락에서, 적분 조건도 만족하는 근계를 결정학적 근계라고 합니다.^[5] 다른 저자들은 조건 2를 생략하고 조건 2를 만족하는 루트 시스템을 축소라고 부릅니다.^[6] 이 글에서는 모든 뿌리 시스템이 축소되고 결정학적인 것으로 가정합니다.

성질 3에서 볼 때, 적분 조건은 β와 그 반사 σ(β)가 α의 정수배만큼 다르다는 것을 말하는 것과 동등합니다. 연산자를 참고합니다.

속성 4로 정의된 제품은 내부 제품이 아닙니다. 반드시 대칭일 필요는 없으며 첫 번째 인수에서만 선형입니다.

랭크-2 루트 시스템

루트 시스템 $A{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$× ${\displaystyle {A\mathrm{}}_{}}$ 1 ${\$	루트 시스템 ${\displaystyle {D2\mathrm{}}_{}}$ ${\$
루트 시스템 ${\displaystyle {A2\mathrm{}}_{}}$ ${\$	루트 시스템 ${\displaystyle {G2\mathrm{}}_{}}$ ${\$
뿌리 시스템 ${\displaystyle {B2\mathrm{}}_{}}$ ${\$	뿌리계 ${\displaystyle {C2\mathrm{}}_{}}$ ${\$

루트 시스템 φ의 순위는 E의 차원입니다. 두 근 시스템은 그들이 걸쳐 있는 유클리드 공간을 공통 유클리드 공간의 상호 직교 부분 공간으로 간주함으로써 결합될 수 있습니다. 오른쪽에 그려진 시스템 A₂, B₂, G와₂ 같이 이러한 조합에서 발생하지 않는 근계는 축소할 수 없다고 합니다.

${\displaystyle 각}$루트${\displaystyle 쌍}$에 대해 $숫자$⟨ x, y ⟩ {\displaystyle \langle x,y\rangle }이 보존되도록 φ를 φ로 보내는 가역적 선형 변환 E → E가 있는 경우 두 루트 시스템(E, φ)과 (E, φ)을 동형이라고 합니다.

루트 시스템 φ의 루트 격자는 φ에 의해 생성된 E의 Z-서브모듈입니다. 이것은 E안에 있는 격자입니다.

웨일군

φ의 뿌리와 관련된 초평면을 통한 반사에 의해 생성된 E의 동위원소 그룹을 φ의 웨일 그룹이라고 합니다. 유한 집합 φ에 충실하게 작용하기 때문에 웨일기는 항상 유한합니다. 반사면은 뿌리에 수직인 초평면으로, ${\displaystyle {아래\mathrm{}}_{}}$ 그림에서 A2 ${\$에 점선으로$$ 표시됩니다. 바일군은 6개의 원소를 가진 정삼각형의 대칭군입니다. 이 경우, Weyl 그룹은 뿌리 시스템의 완전한 대칭 그룹이 아닙니다(예: 60도 회전은 뿌리 시스템의 대칭이지만 Weyl 그룹의 요소는 아닙니다).

예제 순위 지정

0이 아닌 두 벡터${\displaystyle }${${\displaystyle \alpha ,\mathrm{-\alpha }}$ ${\displaystyle \}}$ ${\displaystyle \{\alpha$, -$\alpha \}}$로 구성된 랭크 1의 루트 시스템은 오직 하나입니다$.$ 이 루트 시스템은 ${\displaystyle {A\mathrm{}}_{}}$ 1 ${\$라고 불립니다$.$

두 개의 예제 순위 지정

랭크 2에는${\displaystyle }$σ α(β) =$$β +$n α$ {\displaystyle \sigma _{\alpha}(\beta) =\beta + n\alpha}에 해당하는 네 가지 가능성이 있습니다. 여기서 n = 0, 1, 2, 3 {\display n = 0, 1, 2, 3}에 해당합니다. 오른쪽 그림은 이러한 가능성을 보여주지만 몇 가지 중복이 있습니다. ${\displaystyle A_{}}$ ${\displaystyle {1\mathrm{}}_{}}$× ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$는 ${\displaystyle {D\mathrm{}}_{}}$ $2{\displaystyle {}_{}}$ ${\$와 동형이고$$ $B{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$는 ${\displaystyle {C\mathrm{}}_{}}$ 2 ${\$와 동형입니다$.$

루트 시스템은 생성되는 격자에 의해 결정되지 않습니다. ${\displaystyle A_{1}\times A_{1}}$ and ${\displaystyle B_{2}}$ both generate a square lattice while ${\displaystyle A_{2}}$ and ${\displaystyle G_{2}}$ both generate a hexagonal lattice.

φ가 E의 루트 시스템이고 S가 ψ = φ ∩ S에 의해 스팬된 E의 부분 공간일 때마다 ψ는 S의 루트 시스템입니다. 따라서 순위 2의 4개의 루트 시스템의 전체 목록은 임의의 순위의 루트 시스템에서 선택된 임의의 2개의 루트에 대한 기하학적 가능성을 보여줍니다. 특히 그런 두 뿌리는 0도, 30도, 45도, 60도, 90도, 120도, 135도, 150도, 180도의 각도로 만나야 합니다.

반단순 리 대수에서 발생하는 근계

$g{\displaystyle \mathfrak{}}$ ${\$가 복소 반단순 리 대수이고, $h{\displaystyle \mathfrak{}}${\$displaystyle {\mathfrak {h}}$가 카르탕 부분대수라면, 우리는 다음과 같이 근계를 구성할 수 있습니다. We say that ${\displaystyle \alpha \in {\mathfrak {h}}^{*}}$ is a root of ${\displaystyle {\mathfrak {g}}}$ relative to ${\displaystyle {\mathfrak {h}}}$ if ${\displaystyle \alpha \neq 0}$ and there exists some ${\displaystyle X\neq 0\in {\mathfrak {g}}}$ such that

$모든 H$∈ h ${\displaystyle H$\in ${\mathfrak$ $\{$h}}에 대하여, 근의 집합이 근계를 이루는 내적이 존재함을 보일 수 있습니다. $g{\displaystyle \mathfrak{}}$ ${\$의 근계는 $g{\displaystyle \mathfrak{}}$ ${\$의 구조를 분석하고$$ 표현을 분류하기 위한 기본 도구입니다$$. (Root systems 및 Lie 이론에 대한 아래의 섹션을 참조하십시오.)

역사

뿌리 체계의 개념은 1889년경 빌헬름 킬링에 의해 처음 소개되었습니다 (독일어, Wurzel^[10] system).^[11] 그는 복소수 분야에 걸쳐 모든 단순한 리 대수를 분류하기 위해 그것들을 사용했습니다. Killing은 원래 분류에서 실수를 저질렀는데, 두 개의 예외적인 4등급 뿌리 체계를 나열했는데, 실제로는 하나밖에 없는데, 지금은 F로₄ 알려져 있습니다. Cartan은 나중에 Killing의 두 근 체계가 동형이라는 것을 보여줌으로써 이 오류를 수정했습니다.^[12]

킬링은 현재 카르탄 $부분대수$ ${\displaystyle {\mathfrak {h}}$라고 불리는 것을 고려하여$$리 대수 L ${\displaystyle L}$의 구조를 조사했습니다$.$ 그런 다음 그는 특성 다항식 ${\displaystyle 데트({ad}_{}}$ ${\displaystyle L}$ ⁡$$x - t) ${\displaystyle \det(\operatorname {ad$}_${$L$\}$x-t)}의 근을 연구했습니다. $여기$서 $x$ ∈ h는 ${\mathfrak${h}}에서 ${\$$displaystyle$ x\를 표시합니다. 여기서$$근은 h {\$displaystyle {\mathfrak$ {h}}의$함수$로 또는 $실제로$는$$이중 $벡터 공간$ h$$∗ {\$displaystyle$ $\{\backslash$mathfrak {h}^{*}}의 요소로 간주됩니다. $이$ 근들의 집합은 위에서 정의한$바$와 같이 h ∗ {\$displaystyle {\$mathfrak$${h}}^{*} 안에서 근계를 형성하며, 여기서 내부 생성물은 Killing 형태입니다.

근계 공리의 기본 결과

두 근 사이의 각도의 코사인은 양의 정수 제곱근의 1/2로 제한됩니다. ${\displaystyle 이}$는${\displaystyle }$⟨ $β$$,$ $α$⟩ {\$displaystyle$ \langle \beta,\alpha \rangle } 및 ⟨ β ⟩ {\displaystyle \langle \alpha,\beta \rangle }가 모두 가정에 의한 정수이기 때문입니다.

$2$ ${\displaystyle \cos }$⁡$($θ)${\displaystyle }$∈ [ - 2, $2]$ {\${\displaystyle displaystyle}$ 2${\displaystyle \frac{}{}}$cos(\theta )\in [-2, 2]}에서 cos$$⁡(θ) ${\$displaystyle \cos(\theta)}에 사용할 수 있는$$유일한 값은 0, ± 12, ± 22, ± 32 {\displaystyle 0,\tfrac {1}{2},\pm {\tfrac {\sqrt {2}},$\pm {\tfrac {\sqrt {3}}{2}}$ 및$$± ${\displaystyle \frac{}{}}$$=$${\displaystyle }$±1 {\displaystyle \pm {\tfrac {\sqrt {4}}{2}}$=$\pm 1}, 90°, 60° 또는 120°, 45° 또는 135°, 30° 또는 150° 및 0° 또는 180°의 각도에 해당합니다. 조건 2는 1과 -1 이외의 α의 스칼라 배수는 뿌리가 될 수 없으므로 2α 또는 -2α에 해당하는 0 또는 180°가 빠집니다. 오른쪽 그림은 60° 또는 120°의 각도가 동일한 길이의 뿌리에 해당하는 반면, 45° 또는 135°의 각도는 $2{\displaystyle \sqrt{\mathrm{}}}$ ${\$의 길이 비율에 해당하고 30° 또는 150°의 $각도$는 3$${\$displaystyle {\sqrt {3}}$의 길이 비율에 해당합니다$.$

요약하면, 여기 각 뿌리 쌍에 대한 유일한 가능성이 있습니다.^[13]

• 90도 각도, 이 경우 길이 비율은 제한이 없습니다.
• 각도는 60도 또는 120도, 길이 비율은 1입니다.
• 45도 또는 135도 각도, 길이 비율은 $2{\displaystyle \sqrt{\mathrm{}}}$ ${\$입니다$.$
• 각도 30 또는 150도, 길이 비율은 $3{\displaystyle \sqrt{\mathrm{}}}$ ${\$입니다$.$

양근과 단순근

근 체계$$φ${\$displaystyle \Phi}가 주어지면, 우리는 항상 양의 근들의 집합을 (여러 가지 방법으로) 선택할 수 있습니다. 이것은 φ${\displaystyle$ \Phi}의 하위 집합$$φ + {\displaystyle$$\$Phi$ $^{+}$이므로 다음과 같습니다.

• 각 루트 $\alpha$ ∈ φ ${\displaystyle \{\backslash }$displaystyle \alpha $\$in \Phi}에 대해 $루트$ α ${\$displaystyle \alpha }, - α {\displaystyle -\alpha ${\displaystyle {}^{}}$ 중 정확히 하나가 φ display + {\displaystyle \Phi ^{+}에 포함되어 있습니다.
• ${\displaystyle \mathrm{임의}}$의 두${\displaystyle }개$의$$의 α,$$β ∈ φ + ${\displaystyle$\alpha,\beta \in \Phi ^{+}에서 α + β {\displaystyle \alpha +\beta }가 루트가 되도록 α + β φ ∈ + {\displaystyle \alpha +\beta \in \Phi ^{+}.

양의 근 집합$$φ + {\displaystyle$$\Phi^{+}}을 선택하면$$-$$φ +${\displaystyle$ -\Phi^{+}의 요소를 음의 근이라고 합니다. 어떤 근도 포함하지 않는 초평면 $V$ ${\displaystyle V}$를 선택하고 V ${\displaystyle$ V$\}$의 $고정$된$$변에 놓여 있는 모든 근을$$φ + ${\displaystyle$\Phi^{+}로 설정하여 양의 근의 집합을 구성할 수 있습니다. 또한 모든 양의 근의 집합은 이러한 방식으로 발생합니다.

φ$$+ ${\$displaystyle \Phi$$^{+}의 요소를 {\displaystyle \Phi ^{+}의 두 요소의 합으로 쓸 수 없는 경우 단순 루트(기본 루트$)$라고 합니다. (단순 루트의 집합을 φ φ {\displaystyle \Phi }의 베이스라고도 합니다.) 단순 루트의 집합$$δ${\$displaystyle$$\Delta }은(는) 다음과 같은 추가 특수 속성을 가진 E ${\displaystyle$ E}의$$기초입니다.

• 모든 루트 $\alpha$ ∈ φ ${\$displaystyle \alpha$$\in \Phi}는 정수 계수를 가진$$δ with$${\displaystyle \Delta } 요소의 선형 조합입니다.
• 각 $\alpha$ ∈ φ${\$displaystyle \alpha$$\in \Phi}에 대해 이전 점의 계수는 모두 음수가 아니거나 모두 양수가 아닙니다.

각 루트 시스템$$φ${\$displaystyle \Phi}에 대해 양의 루트 집합 또는 이와 동등하게 단순 루트 집합을 선택할 수 있지만, 양의 루트 집합 두 개는 Weyl 그룹의 작용에 따라 다릅니다.

이중근계, 코루트 및 적분요소

이중근계

만약 φ가 E의 근계라면, 근 α의 근 α는 다음과 같이 정의됩니다.

또한 E에서 코루트 집합은 이중 루트 시스템(또는 때로는 역 루트 시스템)이라고 불리는 루트 시스템 φ를 형성합니다. 정의에 따라 α = α이므로 φ는 φ의 이중근계입니다. φ에 의해 스팬된 E의 격자는 코루트 격자라고 불립니다. φ와 φ는 모두 W에 있는 와일기가 같고, 예를 들어,

δ가 φ에 대한 단순 근들의 집합이라면, δ는 φ에 대한 단순 근들의 집합입니다.

아래에 설명된 분류에서 ${\displaystyle {A형}_{}}$ ${\$ 및 ${\displaystyle {Dn}_{}}$ ${\$의 루트 시스템은 예외적인 루트 $시스템$인 E${\displaystyle {}_{}{6\mathrm{}}_{}}$, ${\displaystyle {E\mathrm{}}_{}}$7, ${\displaystyle {E\mathrm{}}_{}}$ 8${\displaystyle {}_{}}$ ${\displaystyle {F\mathrm{}}_{}}$ 4${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}${\$displaystyle E_{6}, E_{7}, E_{8}, F_{4}, G_{2}$의 루트 시스템은$$ 모두 자체 이중입니다. 즉, 이중 루트 시스템이 원래 루트 시스템과 동형임을 의미합니다. 대조적으로 ${\displaystyle {Bn}_{}}${\$displaystyle B_{n}}$ 및 ${\displaystyle {Cn}_{}}${\$displaystyle C_{n}}$ 루트 시스템은 서로 이중이지만 동형이 아닙니다($n$ = ${\displaystyle 2}${\$displaystyle$n = 2$}$인 경우 제외).

적분요소

E의 벡터$$λ {\displaystyle$$\lambda}는 각 코루트를 갖는 내적이 정수일 경우 적분이라고 합니다.

\Delta }에서$α$∈ δ$$${\$$displaystyle$\$alpha$$$^{\vee }${\displaystyle }집합$은 이중 루트 시스템의 기본을 형성하므로 {\displaystyle \lambda } λ이 통합되어 있는지 확인하려면 위 조건에서 α ∈ δ {\displaystyle \alpha \in \Delta }를 확인하면 됩니다.

적분 원소들의 집합을 주어진 근계와 관련된 무게 격자라고 합니다. 이 용어는 적분 요소가 유한 차원 표현의 가능한 가중치를 형성하는 반단순 리 대수의 표현 이론에서 비롯되었습니다.

뿌리 체계의 정의는 뿌리 자체가 필수 요소임을 보장합니다. 따라서 뿌리의 모든 정수 선형 조합도 적분입니다. 그러나 대부분의 경우 뿌리의 정수 조합이 아닌 적분 요소가 있을 것입니다. 즉, 일반적으로 무게 격자는 뿌리 격자와 일치하지 않습니다.

Dynkin diagram에 의한 뿌리계 분류

루트 시스템은 (α, β) = 0 {\displaystyle(\alpha, β) φ φ ∪ 1 φ \ 2${\$displaystyle \Phi =\Phi _{1}\cup \Phi _{2}의 결합으로 분할할 수 없는 경우 축소할 수 없습니다. (α, β) = 0 {\displaystyle (\alpha,${\displaystyle \backslash }$$beta$)$=$0} $모든$ ${\displaystyle {\alpha }_{}}$ $∈$ $φ$$$1 ${\displaystyle \$alpha \in \Phi _{1}} 및 β $∈$ $φ$ 2 {\displaystyle \$beta$ \in \Phi _{2}.

환원 불가능한 근 체계는 유진 다이킨의 이름을 딴 다이킨 도표인 특정 그래프에 해당합니다. 이러한 그래프의 분류는 조합론의 단순한 문제이며, 환원 불가능한 근 시스템의 분류를 유도합니다.

Dynkin 다이어그램 구성

루트 시스템이 주어지면 앞 절과 같이 단순 루트의 집합 δ을 선택합니다. 연관된 Dynkin 다이어그램의 정점은 δ의 루트에 해당합니다. 모서리는 각도에 따라 다음과 같이 꼭짓점 사이에 그려집니다. (단순 뿌리 사이의 각도는 항상 90도 이상입니다.)

• 벡터가 직교하면 가장자리가 없습니다.
• 120도 각도를 만들면 방향이 없는 단일 모서리,
• 135도 각도를 만들면 방향성 이중 모서리가 있고,
• 각도가 150도인 경우 방향 삼중 모서리입니다.

"방향 에지"란 이중 및 삼중 에지가 짧은 벡터를 가리키는 화살표로 표시되는 것을 의미합니다. (화살을 "보다 큰" 기호로 생각하면 화살표가 어느 방향을 가리키게 되어 있는지 명확하게 알 수 있습니다.)

위에서 언급한 뿌리의 기본 속성에 의해 Dynkin 다이어그램을 생성하는 규칙도 다음과 같이 설명할 수 있습니다. 근이 직교하는 경우 모서리 없음; 비직교근의 경우, 길이 대 길이 비율이 $1{\displaystyle \sqrt{\mathrm{}}}$, 2 ${\$ 3 ${\$sqrt {$3$인 경우, 예를 $들어{\displaystyle \sqrt{\mathrm{}}}$$$ {\$displaystyle G_{$2}}근$$ 시스템의 경우, 150도 각도에서 두 개의 단순 근이 있습니다($길이{\displaystyle \sqrt{\mathrm{}}}$ 비율은 3$${\$displaystyle${\$sqrt {3}}).$ 따라서 Dynkin 다이어그램은 두 개의 정점이 삼중 간선으로 연결되어 있으며, 화살표는 긴 루트와 관련된 정점에서 다른 정점을 가리키고 있습니다. (이 경우 화살표는 어느 방향으로 이동하든 동일하므로 화살표는 약간 중복됩니다.)

뿌리계 분류

주어진 근계에 둘 이상의 가능한 단순 근들의 집합이 있지만, 와일 그룹은 그러한 선택들에 대해 일시적으로 작용합니다.^[19] 따라서 Dynkin 다이어그램은 단순한 뿌리의 선택과는 무관하며 뿌리 체계 자체에 의해 결정됩니다. 반대로, 동일한 Dynkin 다이어그램을 가진 두 개의 뿌리 시스템이 주어지면, 기본에 있는 뿌리부터 시작하여 뿌리를 연결하여 시스템이 실제로 동일함을 보여줄 수 있습니다.^[20]

따라서 루트 시스템을 분류하는 문제는 가능한 Dynkin 다이어그램을 분류하는 문제로 줄어듭니다. 루트 시스템은 Dynkin 다이어그램이 연결된 경우에만 축소할 수 없습니다.^[21] 연결 가능한 다이어그램은 그림에 표시된 것과 같습니다. 첨자는 다이어그램의 정점 수(따라서 해당 축소 불가능한 근 시스템의 순위)를 나타냅니다.

φ${\displaystyle$\$Phi$ }이 루트 시스템인 경우, 이중 루트 시스템 φ ∨ {\displaystyle \Phi^{\vee }}에 대한 Dynkin 다이어그램은 모든 정점과 가장자리를 동일하게 유지하되 모든 화살표의 방향을 반대로 하여 φ {\displaystyle \Phi }의 Dynkin 다이어그램에서 가져옵니다. 따라서 Dynkin 다이어그램을 $통해{\displaystyle {}_{}}$ ${\displaystyle {Bn}_{}}${\$displaystyle B_{n}}$과 ${\displaystyle {Cn}_{}}${\$displaystyle C_{n}$이 서로 이중임을 알 수 있습니다.

와일 챔버와 와일 그룹

φ$$⊂ E {\displaystyle \Phi \subset E}가 루트 시스템인 경우, 각 루트 α {\displaystyle \alpha}에 수직인 초평면을 고려할 수 있습니다. σ$α$ {\displaystyle \$sigma_{\$alpha}}는 초평면에 대한 반사를 나타내며, Weyl 그룹은 모든 σ α {\displaystyle \sigma_{\alpha}'s에 의해 생성된 E {\displaystyle E} 변환 그룹임을 기억하십시오. 초평면 집합의 보체는 연결이 끊어지고 연결된 각 구성 요소를 웨일 챔버라고 합니다. 단순 근의 특정 집합 δ을 수정한 경우, \Delta ∈의 모든 α ∈ δ {\displaystyle \alpha \에 대해 (α$,$ v) > $0 {\$$displaystyle$ $,v$) > 0$}$과 같은 점 V δ$$E {\\in }$$으로 기본 Weyl 챔버를 정의할 수 있습니다.

반사${\displaystyle }$σ ${\displaystyle \mathrm{\alpha }},$ α ∈ φ${\displaystyle$ \sigma_${\alpha$},\alpha \in \Phi}의 반사는 φ {\displaystyle \Phi }를 보존하기 때문에 뿌리에 수직인 초평면 집합도 보존합니다. 따라서, 각 Weyl 그룹 요소는 Weyl 챔버를 허용합니다.

그림은 ${\displaystyle {A2\mathrm{}}_{}}$ ${\$ 루트$$ 시스템의 경우를 보여줍니다. 뿌리에 직교하는 "초평면"(이 경우 1차원)은 점선으로 표시됩니다. 6개의 60도 섹터는 Weyl 챔버이며 음영이 표시된 영역은 표시된 베이스와 관련된 기본 Weyl 챔버입니다.

와일 챔버에 관한 기본적인 일반 정리는 다음과 같습니다.^[22]

정리: 웨일 그룹은 웨일 챔버에서 자유롭게 그리고 일시적으로 작용합니다. 따라서 웨일 그룹의 순서는 웨일 챔버의 수와 같습니다.

${\displaystyle {예}_{}}$를 들어$$A 2 {\$displaystyle$A_{$2}}$ 케이스에서$$, 웨일 그룹은 6개의 원소를 가지고 있고 6개의 웨일 챔버가 있습니다.

관련 결과는 다음과 같습니다.^[23]

정리: Weyl 챔버 $C$ ${\displaystyle$ C$}$을(를) $고칩니다$ 그러면 모든 $v$∈ E ${\displaystyle$v\in E}에 대해 V ${\displaystyle$ v}의 $Weyl-orbit$는$$C$\{\backslash$displaystyle $C$}의$$닫힘 C ¯${\displaystyle$${\$bar {C}}에 정확히 한 점을 포함합니다.

근계와 거짓말 이론

환원 불가능한 근 체계는 리 이론에서 여러 관련 객체를 분류하며, 특히 다음과 같습니다.

• 단순 복소 리 대수(반단순 리 대수에서 발생하는 근계에 대한 위의 논의 참조),
• 단순 모듈로 센터인 복잡한 Lie 그룹을 간단히 연결하고,
• 간단한 모듈로 센터인 콤팩트 리 그룹을 간단히 연결합니다.

각 경우에 근은 인접 표현의 0이 아닌 가중치입니다.

이제 우리는 험프리스의 주장에$$따라 환원 불가능한 루트 시스템이 C ${\$에 대해 간단한 리 대수를 어떻게 분류하는지에 대한 간단한 표시를 제공합니다.^[24] 예비 결과는 연관된 근 시스템이 축소할 수 없는 경우에만 반단순 리 대수가 간단하다는 것을 나타냅니다.^[25] 따라서 우리는 축소할 수 없는 뿌리 시스템과 단순한 Lie 대수에 대한 관심을 제한합니다.

• 먼저, 각각의 단순 대수 $g{\displaystyle \mathfrak{}}$ ${\$에 대하여 오직 하나의 근계가 존재함을$$ 증명해야 합니다. $이{\displaystyle \mathfrak{}}$ 주장은 g ${\$의 카탄 하위 대수가 자동 형태론에 고유하다는$$ 결과에서 비롯되며,^[26] 그 결과 두 카탄 하위 대수는 동형 근계를 제공합니다.
• 다음으로, 우리는 환원 불가능한 각각의 근 시스템에 대해 최대 하나의 Lie 대수가 있을 수 있다는 것, 즉 근 시스템이 최대 동형까지 Lie 대수를 결정한다는 것을 보여주어야 합니다.^[27]
• 마지막으로, 우리는 각각의 환원 불가능한 근 시스템에 대해 연관된 간단한 Lie 대수가 있다는 것을 보여주어야 합니다. 이 주장은 A형, B형, C형, D형의 근계에 대해 명백하며, 관련된 Lie대수는 고전 Lie대수입니다. 그런 다음 예외적인 대수를 사례별 방식으로 분석할 수 있습니다. 또는 세레의 관계를 이용하여 근 시스템으로부터 Lie 대수를 구축하는 체계적인 절차를 개발할 수 있습니다.^[28]

예외적 근계와 그들의 Lie 그룹과 Lie 대수 사이의 연결에 대해서는 E₈, E, E₇, F₆₄, G를₂ 참조하십시오.

환원 불가능한 근계의 성질

${\displaystyle \Phi}$	${\displaystyle \Phi}$	${\displaystyle \Phi^{<}}}$	I	D	${\displaystyle W}$
An (n ≥ 1)	n(n+1)			n + 1	(n+1)!
B(n ≥ 2)	2n2	2n	2	2	2nn!
C(n ≥ 3)	2n2	2n(n − 1)	2n−1	2	2nn!
D(n ≥ 4)	2n(n − 1)			4	2nn−1!
마6	72			3	51840
마7	126			2	2903040
마8	240			1	696729600
바4	48	24	4	1	1152
사2	12	6	3	1	12

환원 불가능한 루트 시스템은 해당 연결된 Dynkin 다이어그램에 따라 이름이 지어집니다. 4개의 무한 가군(A_n, B, C_n, D_nn, 고전적 근계라고 함)과 5개의 예외적인 경우(예외적 근계)가 있습니다. 첨자는 루트 시스템의 순위를 나타냅니다.

축소할 수 없는 근 시스템에서는 길이(α, α)에 대해 최대 두 개의 값이 있을 수 있으며,^1/2 이 값은 짧고 긴 근에 해당합니다. 모든 뿌리의 길이가 같으면 정의에 따라 길이가 긴 것으로 간주되며 뿌리 시스템은 단순히 레이스로 연결되어 있다고 합니다. 이것은 A, D 및 E의 경우에 발생합니다. 길이가 같은 임의의 두 뿌리는 바일 그룹의 같은 궤도에 놓여 있습니다. 단순하게 배치되지 않은 경우 B, C, G 및 F의 경우, 근 격자는 짧은 근에 의해 스팬되고 긴 근은 하위 격자에 걸쳐 있으며, 이는 코루트 격자의² r/2배와 동일하며, 여기서 r은 긴 근의 길이입니다.

상기 인접한 표에서, φ은 단근의 수를 나타내고, I는 장근에 의해 생성된 부격자의 근 격자 내의 지수를 나타내며, D는 카탄 행렬의 행렬식을 나타내고, W는 웨일기의 차수를 나타내는 것을 특징으로 하는 방법.

환원 불가능한 근계의 명시적 구성

A_n

A의₃ 단순근

	e1	e2	e3	e4
α1	1	−1	0	0
α2	0	1	−1	0
α3	0	0	1	−1

E를 좌표가 0으로 합하는 R의 부분공간이라 하고, φ를 길이 √2의 E 안에 있는 벡터들의 집합, 즉 R 안에 있는 정수 좌표를 갖는 벡터들의 집합이라 합니다. 이러한 벡터는 두 개의 좌표를 제외한 모든 좌표가 0이고, 하나의 좌표는 1이고, 하나의 좌표는 -1이어야 하므로 모두² n+n의 근이 존재합니다. 표준기저로 표현되는 단순근의 한 가지 선택은 1 ≤ i ≤ n에 대한 α = e - e 입니다.

α에 수직인 초평면을 통한 반사 σ은 인접한 i번째 좌표와 (i + 1)번째 좌표의 순열과 같습니다. 이러한 전위는 전체 순열 그룹을 생성합니다. 인접한 단순근에 대해서는 σ(α) = α + α = σ(α) = α + α 즉, 반사는 1의 배수를 더하는 것과 같으나, 인접하지 않은 단순근에 수직인 단순근의 반사는 0의 배수만큼 달라지지 않고 그대로 유지됩니다.

A_n 근 격자, 즉 A_n 근들에 의해 생성된 격자는 성분들의 합이 0인 R의ⁿ⁺¹ 정수 벡터들의 집합으로 가장 쉽게 설명됩니다.

A₂ 근 격자는 삼각 타일의 꼭짓점 배열입니다.

A₃ 뿌리 격자는 결정학자들에게 면심 입방정(또는 입방정) 격자로 알려져 있습니다.^[29] 사면체-팔면체 벌집의 꼭짓점 배열입니다.

A₃ 루트 시스템(다른 랭크 3 루트 시스템과 마찬가지로)은 Zometool Construction 집합에서 모델링할 수 있습니다.^[30]

일반적으로 A근_n 격자는 n차원 단순 벌집의 꼭짓점 배열입니다.

B_n

B의₄ 단순근

	e1	e2	e3	e4
α1	1	−1	0	0
α2	0	1	−1	0
α3	0	0	1	−1
α4	0	0	0	1

E = R이라고 하고, φ는 길이 1 또는 √2의 E 안에 있는 모든 정수 벡터로 구성된다고 합니다. 뿌리의 개수는 총 2개입니다². 1 ≤ i ≤ n – 1의 경우 α = e – e (A의 경우 위의 단순근 선택)이며, 더 짧은 근 α = e입니다.

근단 α에 수직인 초평면을 통한 반사 σ은 물론 단순히 n번째 좌표의 음수입니다. 긴 단순근 α의 경우, σ(α) = α + α이지만, 짧은근에 수직인 반사의 경우, σ(α) = α + 2α로, 1의 배수가 아닌 2의 배수로 차이가 납니다.

B근_n 격자, 즉 B근에_n 의해 생성된 격자는 모든 정수 벡터로 구성됩니다.

B는 √2에 의한 스케일링을 통해 A와 동형이며, 따라서 별개의 루트 시스템이 아닙니다.

C_n

C의₄ 단순근

	e1	e2	e3	e4
α1	1	−1	0	0
α2	0	1	−1	0
α3	0	0	1	−1
α4	0	0	0	2

E = R이라고 하고, E φ는 E의 모든 정수 벡터와 함께 길이 √2의 모든 정수 벡터로 구성되며, 여기서 λ는 길이 1의 정수 벡터입니다. 뿌리의 개수는 총 2개입니다². 단순근의 한 가지 선택은 α = e - e이고, 1 ≤ i ≤ n - 1 (A에 대한 단순근의 위 선택)에 대한 것이고, 더 긴 근 α = 2e입니다. 반사 σ(α) = α + α이지만 σ(α) = α + 2α입니다.

C_n 루트 격자, 즉 C_n 루트에 의해 생성된 격자는 성분의 합이 짝수 정수인 모든 정수 벡터로 구성됩니다.

C는 √2에 의한 스케일링과 45도 회전을 통해 B와 동형이며, 따라서 뚜렷한 근계가 아닙니다.

D_n

D의₄ 단순근

	e1	e2	e3	e4
α1	1	−1	0	0
α2	0	1	−1	0
α3	0	0	1	−1
α4	0	0	1	1

E = R이라고 하고, φ는 길이 √2의 E 안에 있는 모든 정수 벡터로 구성된다고 합니다. 총 뿌리 수는 2n(n - 1)입니다. α = e + e와 함께 1 ≤ i ≤ n - 1 (A에 대한 위의 단순한 뿌리 선택)에 대한 단순한 뿌리의 한 가지 선택.

α에_n 수직인 초평면을 통한 반사는 인접한 n번째 및 (n - 1)번째 좌표를 전치 및 음화하는 것과 같습니다. 단순한 근과 다른 단순한 근에 수직한 반사는 더 큰 배수가 아니라 두 번째 근의 0 또는 1의 배수만큼 다릅니다.

D_n 근 격자, 즉 D_n 근에 의해 생성된 격자는 성분의 합이 짝수 정수인 모든 정수 벡터로 구성됩니다. 이것은_n C 근 격자와 같습니다.

D_n 근은 정류된 n-정소플렉스의 정점으로 표현됩니다. Coxeter-Dynkin 다이어그램: ... 2n(n - 1)개의 꼭짓점은 n-정소플렉스의 가장자리 가운데에 존재합니다.

D는₃ A와₃ 일치하므로 뚜렷한 근계가 아닙니다. 12개의₃ D 루트 벡터는 정육면체의 더 낮은 대칭 구성의 정점으로 표현됩니다.

D는₄ 삼중성이라고 불리는 추가 대칭을 가지고 있습니다. 24개의₄ D 루트 벡터는 24개 셀의 더 낮은 대칭 구성의 정점으로 표현됩니다.

E₆, E₇, E₈

1의22 72개의 정점은6 E의 근 벡터를 나타냅니다. (이 E6 Coxeter 평면 투영에서는 녹색 노드가 두 배로 증가합니다.)	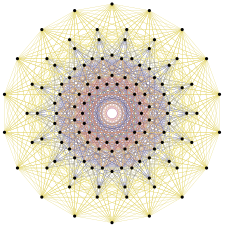2의31 126개 정점은 E의 근 벡터를7 나타냅니다.	4개의21 정점 중 240개는 E의8 근 벡터를 나타냅니다.

• E₈ 근계는 R의⁸ 임의의 벡터 집합으로 다음 집합과 합동입니다.
  $${\displaystyle D_{8}\cup \left\{\frac {1}{2}}\left(\sum_{i=1}^{8}\varepsilon_{i}\mathbf {e}_{i}\right):\varepsilon _{i}=\pm 1,\,\varepsilon _{1}\cdots \varepsilon _{8}=+1\right\}.}$$

  

뿌리 시스템에는 240개의 뿌리가 있습니다. 방금 나열된 집합은 E8 근 격자에서 길이 √2의 벡터 집합으로, 간단히 E8 격자 또는 γ이라고도 합니다. R의⁸ 점들의 집합은 다음과 같습니다.

1. 모든 좌표는 정수이거나 모든 좌표는 반 integers(정수와 반 integers의 혼합은 허용되지 않음)이며,
2. 8개의 좌표의 합은 짝수 정수입니다.

따라서,

• 근계 E는₇ E에서₈ 고정된 근에 수직인 벡터들의₈ 집합입니다. 뿌리 시스템 E는₇ 126개의 뿌리를 가지고 있습니다.
• 근계 E는₆ E에서₇ 고정된 근에 수직인 벡터의₇ 집합이 아닙니다. 실제로 그런 식으로 D를₆ 얻습니다. 그러나 E는₆ E의₈ 적절한 두 뿌리에 수직인 E의₈ 하위 시스템입니다. 뿌리 시스템 E에는₆ 72개의 뿌리가 있습니다.

E의₈ 단순근: 짝수 좌표

1	−1	0	0	0	0	0	0
0	1	−1	0	0	0	0	0
0	0	1	−1	0	0	0	0
0	0	0	1	−1	0	0	0
0	0	0	0	1	−1	0	0
0	0	0	0	0	1	−1	0
0	0	0	0	0	1	1	0
−1/2	−1/2	−1/2	−1/2	−1/2	−1/2	−1/2	−1/2

때때로 편리한 E 격자에 대한 대안적인 설명은 R의 모든 점의 집합 γ'로 다음과 같습니다.

• 모든 좌표는 정수이고 좌표의 합은 짝수, 또는
• 모든 좌표는 반 integers이고 좌표의 합은 홀수입니다.

격자 γ γ'와 γ'는 동형입니다. 임의의 홀수 개의 좌표의 부호를 변경하여 하나에서 다른 하나로 전달할 수 있습니다. 격자 γ은 E에 대한 짝수 좌표계로 불리기도 하고 격자 γ'은 홀수 좌표계로 불리기도 합니다.

대체(비정규) Dynkin 다이어그램(위)에서 노드 순서에 따라 행이 정렬된 짝수 좌표계에서 E에₈ 대한 단순 근의 한 가지 선택은 다음과 같습니다.

α_i = e_i − e_i+1, for 1 ≤ i ≤ 6, and

α = e + e

(D에₇ 대한 단순 근의 위의 선택) 및

E의₈ 단순근: 홀수 좌표

1	−1	0	0	0	0	0	0
0	1	−1	0	0	0	0	0
0	0	1	−1	0	0	0	0
0	0	0	1	−1	0	0	0
0	0	0	0	1	−1	0	0
0	0	0	0	0	1	−1	0
0	0	0	0	0	0	1	−1
−1/2	−1/2	−1/2	−1/2	−1/2	1/2	1/2	1/2

교대(비정규) Dynkin 다이어그램(위)에서 노드 순서에 따라 행이 정렬된 홀수 좌표계에서 E에₈ 대한 단순 근의 한 선택은 다음과 같습니다.

α_i = e_i − e_i+1, for 1 ≤ i ≤ 7

(A에₇ 대한 위의 단순 근 선택)과 함께

α = β, 여기서

$\beta$ = $12$ ($$-$$∑$$ =$$ $je$ + ∑ i = j + 18 e ) . {\textstyle {\frac {1}{2}}\left (-\sum _{i=1}^{j}e_{i}+\sum _{i=j+1}^{8}e_{i}\right).

(β를₃ 사용하면 동형 결과를 얻을 수 있습니다. β 또는_1,7 β를_2,6 사용하면 간단히 A 또는₈ D를₈ 얻을 수 있습니다. β의₄ 경우 좌표가 0으로 합하고, α도_1...7 마찬가지이므로 좌표가 0으로 합하는 7차원 부분 공간에만 걸쳐 있습니다. 실제로 -2β는₄ 밑면(α_i)에 좌표(1,2,3,4,3,2,1)를 가지고 있습니다.

α에₁ 대한 수직은 처음 두 좌표가 동일하다는 것을 의미하므로 E는₇ 처음 두 좌표가 동일한 E의₈ 부분 집합이고, 유사하게 E는₆ 처음 세 좌표가 동일한 E의₈ 부분 집합입니다. 이를₇ 통해 E와 E를₆ 명시적으로 정의할 수 있습니다.

E₇ = {α ∈ Z⁷ ∪ (Z+1/2)⁷ : Σα_i² + α₁² = 2, Σα_i + α₁ ∈ 2Z},

E₆ = {α ∈ Z⁶ ∪ (Z+1/2)⁶ : Σα_i² + 2α₁² = 2, Σα_i + 2α₁ ∈ 2Z}

α를₁ 삭제하고 나서 α를₂ 삭제하면₆ E와₇ E에 대한 단순 근들의 집합을 얻을 수 있습니다. 그러나 이들 단순 근들의 집합은 α₁ 또는 α와₂ 직교하지 않기 때문에 위에서 쓴 것과 다른₈ E₇ 및 E 부분₆ 공간에 있습니다.

F₄

F의₄ 단순근

	e1	e2	e3	e4
α1	1	−1	0	0
α2	0	1	−1	0
α3	0	0	1	0
α4	−1/2	−1/2	−1/2	−1/2

F의 경우, E = R이라고 하고, 2α의 좌표가 모두 정수이고 모두 짝수이거나 모두 홀수인 길이 1 또는 √2의 벡터 α의 집합을 φ라고 합니다. 이 시스템에는 48개의 뿌리가 있습니다. 단순근의 한 가지 선택은 B에 대해 위에 주어진 단순근의 선택, 그리고 α ${}_{}$ =$$- $\underset{}{\overset{}{}}$∑ $i$ = 14 e {\textstyle {\boldsymbol {\alpha}_{4}=-{\frac {1}{2}\sum_{i=1}^{4}e_{i}}입니다.

F근₄ 격자는 모든 좌표가₄ 정수이거나 모든 좌표가 반정수(정수와 반정수의 혼합은 허용되지 않음)가 되도록 R에⁴ 있는 점들의 집합입니다. 이 격자는 후르비츠 4차 이온의 격자와 동형입니다.

G₂

G의₂ 단순근

	e1	e2	e3
α1	1	−1	0
β	−1	2	−1

뿌리 체계 G는₂ 12개의 뿌리를 가지고 있으며, 이는 육각형의 꼭짓점을 형성합니다. 위 사진을 보세요.

단순근의 한 선택은 (α, β = α - α)이고, 여기서 α = e - e for i = 1, 2는 A에 대한 상기 단순근의 선택입니다.

G근₂ 격자, 즉 G근에₂ 의해 생성되는 격자는 A근₂ 격자와 같습니다.

근포셋

양의 근 집합은 $\beta {\displaystyle }$- ${\displaystyle \alpha }$ ${\displaystyle \beta -\alpha }$가 단순 근의 음이 아닌 선형 조합인 $경우$에만 α ${\displaystyle \le }$ ${\displaystyle \beta }$ ${\displaystyle \alpha \leq \beta }$라고 함으로써 자연스럽게 순서가 정해집니다. $\underset{}{\mathrm{이}}$ 포셋은 $\underset{}{데그}$⁡$($∑ α ∈ δ$α$) = ∑$$α ∈ λ α {\textstyle \deg \left(\sum _{\alpha \in \Delta }\lambda _{\alpha \right)=\sum _{\alpha \in \Delta }\lambda _{\alpha }\λ _{\alpha}}로 등급이 매겨지며, 많은 놀라운 조합 특성을 가지고 있습니다. 그 중 하나는 이 포셋으로부터 해당 웨일기의 기본 불변량의 정도를 결정할 수 있다는 것입니다.^[31] Hasse 그래프는 루트 포셋의 순서를 시각화한 것입니다.

참고 항목

• ADE구분
• 아핀근계
• 콕서터-딘킨 도표
• 콕서터군
• 콕서터 행렬
• 덩킨도
• 근일점
• 반단순 리 대수
• 반단순 리 대수의 표현 이론에서의 가중치
• 반단순 리 대수의 근계
• 웨일군

메모들

참고문헌

• Adams, J.F. (1983), Lectures on Lie groups, University of Chicago Press, ISBN 0-226-00530-5
• Bourbaki, Nicolas (2002), Lie groups and Lie algebras, Chapters 4–6 (translated from the 1968 French original by Andrew Pressley), Elements of Mathematics, Springer-Verlag, ISBN 3-540-42650-7루트 시스템의 Bourbaki, Nicolas (2002), Lie groups and Lie algebras, Chapters 4–6 (translated from the 1968 French original by Andrew Pressley), Elements of Mathematics, Springer-Verlag, ISBN 3-540-42650-7고전적인 참조입니다.
• Bourbaki, Nicolas (1998). Elements of the History of Mathematics. Springer. ISBN 3540647678.
• Coleman, A.J. (Summer 1989), "The greatest mathematical paper of all time", The Mathematical Intelligencer, 11 (3): 29–38, doi:10.1007/bf03025189, S2CID 35487310
• Hall, Brian C. (2015), Lie groups, Lie algebras, and representations: An elementary introduction, Graduate Texts in Mathematics, vol. 222 (2nd ed.), Springer, ISBN 978-3319134666
• Humphreys, James (1972). Introduction to Lie algebras and Representation Theory. Springer. ISBN 0387900535.
• Humphreys, James (1992). Reflection Groups and Coxeter Groups. Cambridge University Press. ISBN 0521436133.
• Killing, Wilhelm (June 1888). "Die Zusammensetzung der stetigen endlichen Transformationsgruppen". Mathematische Annalen. 31 (2): 252–290. doi:10.1007/BF01211904. S2CID 120501356. Archived from the original on 2016-03-05.
  • — (March 1888). "Part 2". Math. Ann. 33 (1): 1–48. doi:10.1007/BF01444109. S2CID 124198118.
  • — (March 1889). "Part 3". Math. Ann. 34 (1): 57–122. doi:10.1007/BF01446792. S2CID 179177899. Archived from the original on 2015-02-21.
  • — (June 1890). "Part 4". Math. Ann. 36 (2): 161–189. doi:10.1007/BF01207837. S2CID 179178061.
• Kac, Victor G. (1990). Infinite-Dimensional Lie Algebras (3rd ed.). Cambridge University Press. ISBN 978-0-521-46693-6.
• Springer, T.A. (1998). Linear Algebraic Groups (2nd ed.). Birkhäuser. ISBN 0817640215.

더보기

• Dynkin, E.B. (1947). "The structure of semi-simple algebras". Uspekhi Mat. Nauk. 2 (in Russian). 4 (20): 59–127. MR 0027752.

외부 링크