E7(수학)

수학에서 E는₇ 몇 개의 밀접하게 연관된 Lie 그룹, 선형 대수 그룹 또는 그들의 Lie Algebras e의₇ 이름이며, 모두 치수 133을 가지고 있다; 같은 표기법 E는₇ 7위를 가진 해당 뿌리 격자에 사용된다. E라는₇ 명칭은 A_n, B_n, C_n, D라는_n 라벨이 붙은 4개의 무한 시리즈와 E₆, E₇, E₈, F₄, G라는₂ 라벨이 붙은 5개의 예외적인 사례로 분류된 복합 단순 리알헤브라의 카르탄-킬링 분류에서 유래한다. 따라서₇ E 대수학은 다섯 가지 예외적인 사례 중 하나이다.

(성인) 복합형, 콤팩트 리얼형, 또는 E의₇ 어떤 대수적 버전의 기본 집단은 주기적 집단 Z/2Z이며, 그 외적인 오토모피즘 집단은 사소한 집단이다. 그 기본적 표현의 차원은 56이다.

실제 및 복잡한 형태

E형식의₇ 독특한 복합 리 대수학(complex lie 대수학)이 있는데, 이는 복합 치수 133의 복합 그룹에 해당한다. 복합 치수 133의 복합 보조 Lie 그룹 E는₇ 실제 치수 266의 단순한 실제 Lie 그룹으로 간주할 수 있다. 이것은 기본 그룹 Z/2Z를 가지며, E의₇ 콤팩트한 형태(아래 참조)를 가지는 최대 콤팩트 서브그룹을 가지며, 복잡한 결합에 의해 생성되는 순서 2의 외부 자동모형 그룹을 가진다.

E형의₇ 복잡한 Lie 그룹뿐만 아니라, Lie 대수학에는 네 가지 실제 형태가 있으며, 그에 상응하는 네 가지 실제 형태는 사소한 중심을 가지고 있다(모두 대수학적 이중 커버를 가지고 있고, 그 중 세 개는 더 많은 비알제브라틱 커버를 가지고 있어 더 많은 실제 형태를 부여함) 모두 133 실제 치수 133이다.

기본 그룹 Z/2Z를 가지며 사소한 외부 자동모형 그룹을 갖는 컴팩트 형태(다른 정보가 제공되지 않을 경우 보통 의미한 형태)이다.
분할 형태, EV(또는₇₍₇₎ E)는 최대 소형 서브그룹 SU(8)/{±1), 순서 4의 기본 그룹 주기 및 순서 2의 외부 자동모형 그룹을 가지고 있다.
EVI(또는 E_7(-5))는 최대 소형 서브그룹 SU(2)/SO(12)/(중앙), 기본 그룹 순서 4의 비주기적 그룹 및 사소한 외부 자동화 그룹을 가지고 있다.
EVII(또는 E_7(-25))는 최대 소형 서브그룹 SO(2)/E₆/(중앙), 무한순환 기본 그룹 및 순서 2의 외부 자동모형 그룹을 가지고 있다.

간단한 리알헤브라의 실제 형태에 대한 전체 목록은 단순 리 그룹 목록을 참조하십시오.

E의₇ 콤팩트한 실제 형태는 64차원 특출한 콤팩트 리만 대칭 공간 EVI(카탄의 분류에서)의 등위계 그룹이다. 쿼터니언과 옥토니언의 텐서 생산물인 대수학을 이용해 만들 수 있고, 투사면의 통상적인 공리에는 따르지 않지만 로젠펠드 투사면으로도 알려져 있어 비공식적으로 "쿼터옥토니언 투사면"으로 알려져 있다. 이것은 한스 프로이덴탈과 자크 티츠 때문에 마법의 광장으로 알려진 구조를 사용하여 체계적으로 볼 수 있다.

Tits-Koecher 건설은 27차원 예외적인 요르단 알헤브라스로부터 E₇ Lie 대수학의 형태를 생산한다.

대수군으로서의₇ E

리 대수학의 체발리 기초를 이용하여, 정수에 대한 선형 대수집단으로 E를₇ 정의할 수 있으며, 결과적으로 모든 조합 고리 및 특히 어떤 분야에 걸쳐서 E를 정의할 수 있다: 이것은 소위 분할("불완전"이라고도 함) 부선 형태의 E를₇ 정의한다. 는 대수적으로 문을 닫분야에 걸쳐, 이러하고 이중 커버 있는 유일한 형태; 하지만, 다른 밭에, 갈루아 cohomology의 전반적인 체계하에서(완벽한 분야 k에)설정한 H1(k, Aut(E7)), 때문에 E7(아래 참조)의 Dynkin도 없는 automorphi에 의해서 분류된다 종종 많은 다른 양식 또는 E7의“반전”이 있다.sms는 H¹(k, E_{7, ad})와 일치한다.^[1]

실수를 분야에 걸쳐 세개의 실제 거짓말 그룹에서 기술된 바와 같이 E7을 차지하다 이러한 대수적으로 뒤틀린 형태의 정체성이지만, 섬세함은 근본적인 그룹 관련하여의 실수 구성 요소:E7의 모든 수반 형태 대수 기하학의 의미에서, 그들이 정확히 1doubl 인정한다는 근본적인 그룹 Z/2Z다.e 커버; 따라서₇ E의 비-컴팩트 실제 리 그룹 형태는 대수학적이지 않으며 충실한 유한 차원 표현을 허용하지 않는다.

유한한 분야에 걸쳐, Lang-Steinberg의 정리는 H¹(k, E₇) = 0을 의미하며, E는₇ 뒤틀린 형태가 없다는 것을 의미한다: 아래를 참조하라.

대수학

딘킨 도표

E에₇ 대한 Dynkin 도표는 에 의해 제공된다.

루트 시스템

2개의₃₁ 폴리토프의 126 정점은 이 Coxeter 평면 투영에 나타난 바와 같이 E의₇ 루트 벡터를 나타낸다.
Coxeter-Dynkin 다이어그램:

기본 벡터 [u,v,w]를 사용한 3D 투영에서 H3 대칭:
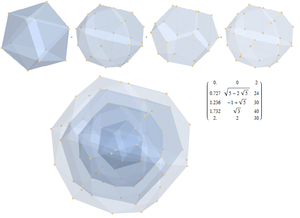
u = (1, φ, 0, -1, φ, 0.0)
v = (sv, 0, 1, φ, 0, -1,0)
w = (0, 1, φ, 0, -1, φ,0)
투영된 2개의₃₁ 폴리토프 정점은 3D 표준에 의해 정렬되고 계산되어 각 집합의 점점 투명한 선체를 생성한다. 다음 프로그램:
1) 원점 2점
2) 이코사면체 2개
3) 아이코사도데카헤드론 1개
4) 도데면체 2개
5) 1 이코사도데카헤드론
총 126정점.

뿌리가 7차원 공간에 걸쳐 있더라도 8차원 벡터 공간의 7차원 아공간에서 베드로 누워 있는 모습을 표현하면 더욱 대칭적이고 편리하다.

뿌리는 (1,-1,0,0,0,0,0,0,0)의 8×7 순열과 ( ${\begin{pmatrix}8\\4\end{pmatrix}}$ ${\begin{pmatrix}8\\4\end{pmatrix}}$ 의 모든 ${\begin{pmatrix}8\\4\end{pmatrix}}$ 순열 (8 $){\begin{pmatrix}\4\\end{pmatrix}}}$ 순열(순열 ${\begin{pmatrix}8\\4\end{pmatrix}}$ , 열, 열, 열, 열, 열, 열, 열, 열, 열, 열, 열)이다.

7차원 아공간은 8개 좌표의 합이 모두 0인 아공간이라는 점에 유의한다. 뿌리는 126개다.

소박한 뿌리는

(0,−1,1,0,0,0,0,0)

(0,0,−1,1,0,0,0,0)

(0,0,0,−1,1,0,0,0)

(0,0,0,0,−1,1,0,0)

(0,0,0,0,0,−1,1,0)

(0,0,0,0,0,0,−1,1)

(½,½,½,½,−½,−½,−½,−½)

이들은 Dynkin 다이어그램의 해당 노드가 사이드 노드와 함께 왼쪽에서 오른쪽으로 정렬되도록 나열되어 있다(위에서 설명한 다이어그램에서).

대체 설명

E₇ × SU(2)를 E의₈ 하위 그룹으로 간주하는 데 유용한 루트 시스템에 대한 대안(7차원) 설명은 다음과 같다.

(± $4\times {\begin{pmatrix}6\\2\end{pmatrix}}$ ,±1,±1, $,$ 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)의 모든 4× ( $){\$ 4 $\time$ {\ $begin{pmatrix}}}$ 순열 $4\times {\begin{pmatrix}6\\2\end{pmatrix}}$ .

\왼쪽(\pm {1\over 2},\pm {1\over 2},\pm {1\over 2},\pm {1\over 2},\pm {1\pm {1\over 2},\pm {\sqrt {2}}\1\pm}\pm {1\cover {2}}\오른쪽)}}}}}

그리고 다음의 두 뿌리는

\left(0,0,0,0,0,0,0,\pm {\sqrt{2}}\오른쪽).

따라서 발전기는 66차원 so(12) 아발지브라와 두 개의 자기 콘주게이트 웨일 스피너로 변환되는 64개의 생성기와 반대편 치례성 치례성 발생기와 그 치례성 발생기 및 기타 치례성 생성기 $({\$ 로 구성된다 $\pm {\sqrt {2}}$

E₇ Cartan 행렬(아래) 및 Dynkin 다이어그램 노드 순서 지정:

단순 루트의 한 선택은 다음 행렬의 행에 의해 주어진다.

{\displaystyle{\begin{bmatrix}1&, -1&, 0&, 0&, 0&, 0&, 0\\0&, 1&, -1&, 0&, 0&, 0&, 0\\0&, 0&, 1&, -1&, 0&, 0&, 0\\0&, 0&, 0&, 1&, -1&, 0&, 0\\0&, 0&, 0&, 0&, 1&, 1&, 0\\-{\frac{1}{2}}&-{\frac{1}{2}}&-{\frac{1}{2}}&-{\frac{1}{2}}&-{\frac{1}{2}}&-{\frac{1}{2}}&.{\frac{\sqrt{2}}{2}}\\0&, 0&, 0&, 0&, 1&, -1&, 0\\\end{bmatrix}}.}

웨일 그룹

E의₇ Weyl 그룹은 순서 2903040: 순서 2의 주기적 그룹과 순서 1451520의 고유한 단순 그룹(PSp₆(2) 또는 PSΩ₇(2)으로 설명할 수 있다.^[2]

카르탄 행렬

단순 루트 위치가 추가된 E7 루트 포셋의 Hasse 다이어그램.

{\begin{bmatrix}2&-1&0&0&0&0&0\\-1&2&-1&0&0&0&0\\0&-1&2&-1&0&0&0\\0&0&-1&2&-1&0&-1\\0&0&0&-1&2&-1&0\\0&0&0&0&-1&2&0\\0&0&0&-1&0&0&2\end{bmatrix}}.

중요한 하위 게브라 및 표현

E는₇ 루트 시스템에 대한 8차원 설명에서 첫 번째 뿌리 그룹이 (E와₇ 동일한 카르탄 하위 골격을 가진) SU(8)의 뿌리와 동일하다는 것을 분명히 알 수 있듯이 SU(8) 하위 골격을 가지고 있다.

133차원 부호 표현 외에도 E₈ 부호 표현에서 찾을 수 있는 56차원 "벡터" 표현이 있다.

실제적이고 복잡한 리알헤브라와 리 그룹의 유한 치수 표현 문자는 모두 웨일 문자 공식에 의해 주어진다. 최소 불가해한 표현 치수는 다음과 같다(OEIS에서 순차 A121736).

1, 56, 133, 912, 1463, 1539, 6480, 7371, 8645, 24320, 27664, 40755, 51072, 86184, 150822, 152152, 238602, 253935, 293930, 320112, 362880, 365750, 573440, 617253, 861840, 885248, 915705, 980343, 2273920, 2282280, 2785552, 3424256, 3635840...

위의 순서에서 밑줄 친 용어는 E의₇ 조정된 형태(동일하게₇, E의 뿌리 격자에 속하는 가중치를 가진 것)로 소유하는 수정 불가능한 표현들의 치수인 반면, 전체 순서는 단순하게 연결된 형태의₇ 수정 불가능한 표현들의 치수를 제공한다. 1903725824, 16349520330 등의 치수에 대한 비이형적 비이성적 표현력이 존재한다.

기본적인 표현은 치수가 133, 8645, 365750, 27664, 1539, 56 및 912인 것이다(위의 카르탄 행렬에 대해 선택한 순서에 따라 Dynkin 다이어그램의 7개 노드에 대응함). 즉, 노드는 6개 노드 체인에 먼저 읽히고 마지막 노드는 세 번째 노드에 연결된다.

E₇ 다항식 불변량

E는₇ 56개의 비확정 변수에서 다음과 같은 쌍의 다항식들의 자동형 그룹이다. 변수를 28, (p, P)와 (q, Q)의 두 그룹으로 나누는데, 여기서 p와 q는 실제 변수, P와 Q는 3×3 옥토니언 은둔자 행렬이다. 첫 번째 불변제는 Sp(56, R):

C_{1}=pq-qp+Tr[PQ]-Tr[QP]

두 번째로 복잡한 불변량은 대칭 사분위수 다항식이다.

C_{2}=(pq+Tr[P\circule Q])^{2}+pTr[]Q\circle {\tild{Q}]+qTr[P\circle {\tilde{P}}+Tr[{\tilde{P}}\circle {\tilde{Q}]

여기서 ${\tilde {P}}\equiv \det(P)P^{-1}$ ~ ${\tilde {P}}\equiv \det(P)P^{-1}$ ${\tilde {P}}\equiv \det(P)P^{-1}$ ( ${\tilde {P}}\equiv \det(P)P^{-1}$ ) ${\tilde {P}}\equiv \det(P)P^{-1}$ - ${\tilde {P}}\equiv \det(P)P^{-1}$ ${\$ 이진원 ${\tilde {P}}\equiv \det(P)P^{-1}$ 연산자는 $A\circ B=(AB+BA)/2$ $A\circ B=(AB+BA)/2$ $A\circ B=(AB+BA)/2$ = $A\circ B=(AB+BA)/2$ $A\circ B=(AB+BA)/2$ + $A\circ B=(AB+BA)/2$ A $A\circ B=(AB+BA)/2$ ) $A\circ B=(AB+BA)/2$ / $A\circ B=(AB+BA)/2$ ${\displaystystyle A\c=(AB+BA)/2}$ 에 의해 정의된다 $A\circ B=(AB+BA)/2$

Cartan에 의해 구성된 대체 사분위수 다항식 불변제는 각각 28개의 구성요소를 가진 두 개의 반대칭 8x8 행렬을 사용한다.

C_{2}=Tr[(XY)^{2}]-{\dfrac {1}{4}}Tr[XY]^{2}+{\frac {1}{96}}\epsilon _{ijklmnop}\left(X^{ij}X^{kl}X^{mn}X^{op}+Y^{ij}Y^{kl}Y^{mn}Y^{op}\오른쪽)

E형₇ 체벌리 그룹

(분할) 대수군 E₇(위 참조)의 q 원소가 있는 유한장 위에 있는 점들은 부선(중심점 없음) 또는 단순하게 연결된 형태(그 대수적 범용 커버)에 의해 유한한 체발리 군을 부여한다. 이것은₇ E(q)라고 쓰여진 그룹과 밀접하게 연결되어 있지만, 이 표기법에는 다음과 같은 몇 가지를 나타낼 수 있는 모호성이 있다.

E의₇ 단순하게 연결된 형태의 F에_q 대한 점들로 구성된 유한 집단(명료성을 위해 E_7,sc(q)로 쓸 수 있으며, E에_q 대한₇ F 타입의 "범용" 체벌리 그룹으로 알려져 있다)
(경직) E의₇ 부선형식의 F에_q 대한 점으로 구성된 유한집단(명료성을 위해 E_7,ad(q)로 표기할 수 있으며, E에₇ 대한_q E형식의 "성인" 체발리 그룹으로 알려져 있다) 또는
전자에서 후자에 이르는 자연지도의 이미지인 유한집단: 이것은 유한집단을 다루는 텍스트에서 가장 흔하게 볼 수 있듯이, 다음에서 E₇(q)로 나타낼 것이다.

다음과 같이 유한 그룹 관점에서, 그 SL(n, q), PGL(n, q)과 PSL(n, q)사이에 유사하다 이 세 집단, 사이의 관계:E7(q)어떤 q, E7,sc(q)은 슈어 커버, E7,ad(q)의 자기 동형 그룹에 놓여 있다 간단하다;게다가 2의 q다 권력 세 사람 모두 일치하고 고르요약할 수 있다.herwise(q)가 홀수일 때) E₇(q)의 슈르 승수는 2이고 E₇(q)는_7,ad E(q)의 지수 2에 해당하므로 E_7,sc(q)와 E_7,ad(q)가 2·E₇(q)와 E₇(q)·2로 표기되는 경우가 많다. 대수군 관점에서 E(q)는 E(q_7,sc_7,ad)와 E(q)와는 달리 F에_q 대한 대수군의 점 집합이 자연적인 방법이 아니기 때문에 유한₇ 단순군을 가리키는 것이 덜 일반적이다.

위에서 언급한 바와 같이 E₇(q)는 어떤 q에 대해서도 단순하며 유한단순집단의 분류에 의해 다루어지는 무한가족 중 하나를 구성한다.^[3]^[4] 원소의 개수는 공식(OEIS에서 순서 A008870)에 의해 주어진다.

{\frac {1}{\mathrm {gcd}(2,q-1)}{63}(q^{18}-1)(q^{14}-1)(q^{12}-1)(q^{10}-1)(q^{8}-1)(q^{6}-1)(q^{1}-1)-1}(q^{gcod-1)}-1)}-1

E_7,sc(q) 또는 E_7,ad(q)의 순서는 분할 계수 gcd(2, q-1)를 제거하여 얻을 수 있다(OEIS에서 순차 A008869). E₇(q)의 슈르 승수는 gcd(2, q-1)이며, 외측 자동성 그룹은 대각선 자동성 그룹 Z/gcd(2, q-1)Z(E_7,ad(q)의 작용으로 주어짐)와 자기장 자동성 그룹(즉, q = p가^f prime인 경우 f의 주기)의 산물이다.

물리학의 중요성

N = 11차원 초중력으로부터의 치수 감소인 4차원의 8초중력은 E보소닉₇ 지구 대칭과 SU(8)보소닉 국부 대칭을 인정한다. 페르미온은 SU(8), 게이지 장은 E를₇ 나타내고 스칼라는 둘 다 나타낸다(그래비톤은 둘 다에 관한 싱글트임). 물리적 상태는 코셋 E₇/SU(8)를 나타낸다.

끈 이론에서 E는₇ (안정적이지 않고 비대칭적인) 이성적인 문자열의 한 버전의 게이지 그룹의 일부로 나타난다. 그것은 또한 4차원 표면 K3와 같은 이성질 끈 이론의 6차원 압축에서 끊기지 않은 게이지 그룹 E₈ × E에서도₇ 나타날 수 있다.

참고 항목

메모들

^ Platonov, Vladimir; Rapinchuk, Andrei (1994) [1991], Algebraic groups and number theory, Pure and Applied Mathematics, 139, Boston, MA: Academic Press, ISBN 978-0-12-558180-6, MR 1278263 (원본: ), §2.2.4
^ Conway, John Horton; Curtis, Robert Turner; Norton, Simon Phillips; Parker, Richard A; Wilson, Robert Arnott (1985). Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups. Oxford University Press. p. 46. ISBN 0-19-853199-0.
^ Carter, Roger W. (1989). Simple Groups of Lie Type. Wiley Classics Library. John Wiley & Sons. ISBN 0-471-50683-4.
^ Wilson, Robert A. (2009). The Finite Simple Groups. Graduate Texts in Mathematics. 251. Springer-Verlag. ISBN 1-84800-987-9.

참조

Adams, J. Frank (1996), Lectures on exceptional Lie groups, Chicago Lectures in Mathematics, University of Chicago Press, ISBN 978-0-226-00526-3, MR 1428422
John Baez, The Octonion, 섹션 4.5: E₇, Bull. 아머. 수학. Soc. 39(2002년), 145-205년. http://math.ucr.edu/home/baez/octonions/node18.html의 온라인 HTML 버전.
E. 크레머와 B. 줄리아, N = 8 초중력 이론 1. 라그랑지안, 체육관Let.B80:48,1978. http://ac.els-cdn.com/0370269378903039/1-s2.0-0370269378903039-main.pdf?_tid=79273f80-539d-11e4-a133-00000aab0f6c&acdnat=1413289833_5f3539a6365149b108ddcec889200964에서 온라인 스캔한 버전.

[1] Platonov, Vladimir; Rapinchuk, Andrei (1994) [1991], Algebraic groups and number theory, Pure and Applied Mathematics, 139, Boston, MA: Academic Press, ISBN 978-0-12-558180-6, MR 1278263 (원본: ), §2.2.4

[2] Conway, John Horton; Curtis, Robert Turner; Norton, Simon Phillips; Parker, Richard A; Wilson, Robert Arnott (1985). Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups. Oxford University Press. p. 46. ISBN 0-19-853199-0.

[3] Carter, Roger W. (1989). Simple Groups of Lie Type. Wiley Classics Library. John Wiley & Sons. ISBN 0-471-50683-4.

[4] Wilson, Robert A. (2009). The Finite Simple Groups. Graduate Texts in Mathematics. 251. Springer-Verlag. ISBN 1-84800-987-9.

[1]

[2]

[3]

[4]

v t 끈 이론
배경	줄들 우주 현 끈 이론의 역사 제1차 슈퍼스트링 제2차 슈퍼스트링 혁명 끈 이론 풍경
이론	난부-고토 액션 폴리아코프 작용 보소닉 끈 이론 슈퍼스트링 이론 I타입 문자열 II형 문자열 IIA 문자열 유형 IIB 문자열 유형 이성질 끈 N=2 슈퍼스트링 F-이론 끈장 이론 매트릭스 문자열 이론 비중요 문자열 이론 비선형 시그마 모형 타키온 응축 RNS 형식주의 GS 포멀리즘
스트링 이중성	T-이중성 S-이중성 U-이중성 몬토넨-올리브 이중성
입자 및 필드	그라비톤 딜라톤 타키온 라몬드-라몬드 필드 칼브-라몬드 필드 자기 단극 이중 그라비톤 이중 광자
브란스	디브레인 NS5-브레인 M2-브레인 M5-브레인 에스브레인 블랙브레인 블랙홀 블랙 스트링 브레인 우주론 떨림 다이어그램 하나니-위튼 전환
등각장 이론	비라소로 대수 거울 대칭 등정 이상 등각대수학 과적합 대수학 정점 연산자 대수 루프 대수 카크무디 대수 베스-주미노-위튼 모형
게이지 이론	이상 징후 인스턴트온 체르-시몬스 양식 보고몰니-프라사드-소머필드 바인딩 예외적인 Lie 그룹(G₂, F₄, E₆, E₇, E₈) ADE 분류 디락 문자열 p-형 전자역학
기하학	칼루자-클레인 이론 압축 왜 10차원이야? 칼러 다지관 리치-플랫 다지관 칼라비-야우 다지관 하이퍼켈러 다지관 K3면 G다지관₂ 스핀(7)-매니폴드 일반화 복합 다지관 오비폴드 코니폴드 오리엔티폴드 모둘리 공간 호하바-위튼 도메인 벽 K-이론(물리학) 꼬인 K이론
초대칭	초중력 초공간 리 수페르게브라 리 슈퍼그룹
홀로그래피	홀로그래피 원리 ADS/CFT 통신
엠이론	매트릭스 M-이론 소개
끈 이론가	아가나기치 아르카니하메드 아티야 은행 베렌슈타인 부소 클리버 커트라이트 딕크라프 디슬러 더글러스 더프 드발리 페라라 피슐러 프리단 게이츠 글리오찌 고파쿠마르 녹색 그린 징그럽다 거버 쿠코프 구스 핸슨 하비 호하바 기븐스 카흐루 카쿠 칼로스 칼루자 카푸스틴 클레바노프 크니즈니크 콘체비치 클라인 린데 몰다세나 만델스탐 마롤프 마르티네크 민왈라 무어 모틀 묵히 마이어스 나노풀로스 네스타세 네크라소프 네베우 닐슨 판 니에우웬후이젠 노비코프 올리브 오오구리 오브루트 폴친스키 폴리아코프 라자라만 라몬드 랜들 랜지바르대미 로체크 롬 사그노티 셰르크 슈바르츠 세이베르크 센 선커 시겔 실버스타인 신 스토다허 스타인하르트 스트로밍거 선드럼 서스킨드 't 후프트' 타운센드 트리베디 투록 바파 베네치아노 베린데 베린데 웨스 비튼 야우 요네아 자몰로드치코프 자몰로드치코프 자슬로 주미노 즈위바흐

Search

E7(수학)

네임스페이스

더

목차

실제 및 복잡한 형태

대수군으로서의₇ E