구조공학 이론

전단 볼트 그림. 상단 그림은 단일 전단을 나타내고 하단 그림은 이중 전단을 나타낸다.

구조 공학은 구조물이 어떻게 자기 무게와 부과된 하중을 지지하고 저항하는지를 이해하고 예측하기 위해 하중, 물리 및 재료에 대한 상세한 지식에 의존한다. 이 지식을 성공적으로 적용하기 위해서는 구조 엔지니어들이 수학 및 관련 경험적 및 이론적 설계 코드에 대한 상세한 지식이 필요할 것이다. 그들은 또한 재료와 구조물의 부식 저항성에 대해 알아야 하며, 특히 그러한 구조물이 외부 환경에 노출되었을 때 더욱 그러하다.

구조물의 설계를 결정하는 기준은 사용성(구조물이 그 기능을 적절하게 수행할 수 있는지 여부를 정의하는 기준) 또는 강도(구조물이 설계 하중을 안전하게 지지하고 저항할 수 있는지를 정의하는 기준)이다. 구조 엔지니어는 이러한 기준을 충족하기에 충분한 강도와 강성을 갖도록 구조물을 설계한다.

구조물에 가해지는 하중은 구조 요소를 통해 전달되는 힘에 의해 지지된다. 이러한 힘은 스스로를 장력(축력), 압축(축력), 전단 및 휨(굽힘 모멘트는 거리 또는 레버 암에 곱한 힘)으로 나타낼 수 있으며, 따라서 회전 효과나 토크가 발생한다.

힘

강도는 재료 특성에 따라 달라진다. 재료의 강도는 축응력, 전단응력, 휨, 비틀림 등에 견딜 수 있는 능력에 따라 달라진다. 재료의 강도는 단위 면적당 힘(제곱 밀리미터 또는 N/mm²당 뉴톤 또는 SI 시스템의 등가 메가파스칼 또는 MPa당 뉴톤, 미국 관습 단위 시스템의 경우 제곱인치 psi당 파운드)으로 측정된다.

구조물은 하중에 의해 유발되는 응력(자재 면적별로 나누어진 힘)이 파괴되지 않고 하중에 저항할 수 있는 구조물의 용량보다 크거나 변형률(백분율 확장)이 너무 커서 원소가 더 이상 기능(수익)을 충족하지 못할 때 강도 기준을 충족하지 못한다.

참고 항목:

강성

강성은 재료 특성과 기하학에 따라 달라진다. 주어진 재료의 구조 요소의 강성은 재료의 영의 계수와 원소의 두 번째 면적 모멘트의 산물이다. 강성은 단위 길이당 힘(밀리미터당 뉴턴 또는 N/mm)으로 측정되며, 후크 법칙에서 '힘 상수'와 같다.

하중을 받는 구조물의 편향은 강성에 따라 결정된다. 동적하중에 대한 구조물의 동적응답(구조물의 고유진동수)도 그 강성에 따라 달라진다.

원소에 힘을 분배하는 표면이 경직된 다중 구조 요소로 구성된 구조에서 원소는 상대 강성에 비례하여 하중을 전달하며, 원소가 강할수록 하중이 더 많이 끌어당긴다. 즉, 편향인 하중/긴장도는 연결된 (접합된) 두 요소에서 동일하게 유지된다. 원소들에 힘을 분배하는 표면이 유연한 구조에서(나무 프레임 구조처럼), 원소들은 상대적인 지류 지역에 비례하여 하중을 운반할 것이다.

구조물은 하중을 받는 동안 허용 가능할 정도로 작은 편향이나 동적 반응을 가지기에 충분히 경직되지 않을 경우 선택된 사용가능성 기준을 충족하지 못하는 것으로 간주된다.

강성의 역행은 유연성이다.

안전계수

구조물의 안전한 설계에는 구조물의 붕괴의 통계적 가능성을 고려한 설계 접근방식이 필요하다. 구조 설계 코드는 하중과 재료 강도는 모두 정규 분포에 따라 다르다는 가정에 기초한다.^{[citation needed]}

구조 엔지니어의 임무는 구조물에 대한 하중 분포와 구조물의 재료 강도 분포 사이의 중복 가능성이 허용될 정도로 작다는 것을 확인하는 것이다(그 기회를 0으로 줄이는 것은 불가능하다).

부분 안전 계수를 하중과 재료 강도에 적용하여 95백분위수(평균으로부터 2 표준 편차)를 사용하여 설계하는 것이 일반적이다. 하중에 적용되는 안전 계수는 일반적으로 실제 하중이 설계 하중보다 95% 더 작다는 것을 보장하며, 강도에 적용되는 계수는 실제 강도의 95%가 설계 강도보다 더 높은 것을 보장한다.

재료 강도에 대한 안전 계수는 재료 및 재료가 국가 또는 지역에 적용되는 설계 코드에 따라 달라진다.

구조 안전 모델링의 보다 정교한 접근방식은 하중과 저항성이 모두 확률적 변수로 모델링되는 구조적 신뢰성에 의존하는 것이다.^[1]^[2] 그러나 이 접근법을 사용하려면 부하 및 저항 분포에 대한 상세한 모델링이 필요하다. 게다가, 그것의 계산은 더 계산 집약적이다.

케이스 로드

하중 케이스는 다양한 유형의 하중과 그에 적용되는 안전 계수의 조합이다. 구조물은 수명주기 동안 경험할 수 있는 모든 하중 케이스에 대해 강도 및 사용가능성을 점검한다.

강도 설계를 위한 일반적인 하중 케이스(초기 부하 케이스, ULS)는 다음과 같다.

1.2 x 사하중 + 1.6 x 활하중

1.2 x 사하중 + 1.2 x 실하중 + 1.2 x 바람하중

서비스 가능성의 설계를 위한 일반적인 하중 케이스(특성 하중 케이스, SLS)는 다음과 같다.

1.0 x 데드 로드 + 1.0 x 라이브 로드

다른 하중 조건에는 다른 하중 케이스를 사용할 수 있다. 예를 들어 화재 설계의 경우 1.0 x 데드 로드 + 0.8 x 라이브 로드의 하중 케이스를 사용할 수 있는데, 화재가 발생하면 모든 사람이 건물을 떠났다고 가정하는 것이 타당하기 때문이다.

다층 건물에서는 모든 층에 동시에 최대 하중이 가해질 확률은 무시할 수 없을 정도로 작기 때문에 지지되는 층수에 따라 총 활하중을 줄이는 것이 보통이다.

대형 건축물이 설계에서 수백 가지의 다양한 하중 케이스를 고려해야 하는 것은 드문 일이 아니다.

뉴턴의 운동 법칙

구조 공학을 위한 가장 중요한 자연 법칙은 뉴턴의 운동 법칙이다.

뉴턴의 첫 번째 법칙은 모든 신체가 정지해 있거나 일률적으로 직진하는 상태에서 끈기 있게 버티는 것을 명시하고 있다. 단, 감명받은 힘에 의해 상태를 바꾸도록 강요되는 한에서는 예외로 한다.

뉴턴의 두 번째 법칙에 따르면 신체의 운동량 변화율은 신체에 작용하는 결과적인 힘에 비례하며 같은 방향이다. 수학적으로 F=ma(힘 = 질량 x 가속)

뉴턴의 제3법칙은 모든 힘은 쌍으로 발생하며, 이 두 힘은 크기가 같고 방향이 반대인 것으로 되어 있다.

이러한 법들로 구조물에 가해지는 힘과 그 구조가 어떻게 저항할 것인지 이해할 수 있다. 제3법칙은 구조가 안정되려면 모든 내외력이 평형을 이루어야 한다고 규정하고 있다. 즉, 자유체 다이어그램에 대한 모든 내부 및 외부 힘의 합계는 0이어야 한다.

$\sum {\vec {F}}=0$ $\sum {\vec {F}}=0$ → $\sum {\vec {F}}=0$ = 0 $\sum {\vec{F}=0$ : 몸에 작용하는 힘의 벡터 합은 0과 같다. 이 번역은 다음과 같다.

σ H = 0: 힘의 수평 구성 요소의 합은 0이다.

σ V = 0: 힘의 수직 성분의 합은 0이다.

$\sum {\vec {M}}=0$ $\sum {\vec {M}}=0$ → $\sum {\vec {M}}=0$ = $\sum {\vec {M}}=0$ $\sum {\vec{M}=0$ : 모든 힘의 모멘트 합계는 0과 같다.

통계적 결정성

구조 엔지니어는 구조 요소와 그 교차점에 있는 노드로 구성된 구조 시스템의 내부 및 외부 힘을 이해해야 한다.

정적으로 결정되는 구조는 뉴턴의 운동 법칙으로부터 평형만을 고려하여 완전히 분석할 수 있다.

정적으로 불확실한 구조는 평형 고려사항으로 공식을 제공할 수 있는 것보다 더 많은 공식을 가지고 있다(동시 방정식 참조). 이러한 시스템은 평형 방정식 외에 기하와 편향의 호환성 방정식을 고려하거나 가상 작업을 사용하여 해결할 수 있다.

시스템이 $b$ $b$ bar $b$ , $j$ $j$ 핀 조인트 $j$ 및 $r$ $r$ 지지 $r$ 반응으로 구성된 경우 다음 관계가 유지되지 않으면 정적으로 결정할 수 없다.

$r+b=2j$

이 관계가 유지된다 하더라도, 구조는 정적으로 불확실한 방식으로 배열될 수 있다.^[3]

탄력성

많은 엔지니어링 설계는 재료가 탄력적으로 작용한다는 가정에 기초한다. 대부분의 재료에서 이 가정은 부정확하지만, 경험적 증거는 이 가정을 사용한 설계가 안전할 수 있다는 것을 보여주었다. 탄력성이 있는 물질은 후크의 법칙을 따르고, 가소성은 일어나지 않는다.

Hoke의 법칙을 따르는 시스템의 경우 생성된 확장은 부하에 정비례한다.

{\vec {\mathbf {F}}}}}}=k{\vec {\mathbf {x}}}}

어디에

x는 평형 위치에서 스프링이 늘어나거나 압축된 거리로, 스프링이 자연적으로 정지할 수 있는 위치[보통 미터 단위]이다.

F는 [보통 뉴턴에서] 물질에 의해 발휘되는 복원력이다.

k는 힘 상수(또는 스프링 상수)이다. 이것이 바로 스프링의 뻣뻣함이다. 상수는 단위 길이당 힘의 단위(일반적으로 미터당 newton)를 가진다.

가소성

Tresca와 Von Mises 기준의 비교

어떤 설계는 재료가 탄력적으로 동작할 것이라는 가정에 기초한다.^[4] 플라스틱 재질은 Hoke의 법칙을 따르지 않는 재료로, 따라서 변형은 적용된 하중에 비례하지 않는다. 플라스틱 재료는 연성 재료다. 가소성 이론은 일부 철근 콘크리트 구조물이 저압력을 받는다고 가정할 때 사용할 수 있는데, 이는 콘크리트가 강재되기 전에 철근 배근에 실패한다는 것을 의미한다.

가소성 이론은 구조물이 붕괴하는 지점(수율)은 하중의 상한과 하한 사이에 있으며, 다음과 같이 정의된다.

주어진 외부 부하에 대해 어느 위치에서든 모멘트가 항복 모멘트를 초과하지 않고 평형 요건을 만족하는 모멘트의 분포를 찾을 수 있으며, 경계 조건이 충족되면 주어진 하중이 붕괴 부하에 대한 하한이다.
작은 변위의 경우, 모든 플라스틱 경첩의 모멘트가 항복 모멘트와 같고 경계 조건이 충족된다고 가정하여 구조물에 의해 수행되는 내부 작업이 동일한 변위의 작은 증분에 대해 주어진 하중에 의해 수행되는 외부 작업과 동일하다고 가정할 때, 그 하중이 공중에 대한 상한이 된다.하중을 줄이다

정확한 붕괴하중이 발견되면 두 방법은 붕괴하중에 대해 동일한 결과를 제공한다.^[5]

가소성 이론은 언제 수율이 발생할 것인지에 대한 정확한 이해에 달려 있다. 플라스틱 재료의 수율 표면에 대한 응력 분포 및 근사치에는 다음과 같은 다양한 모델이 존재한다.^[6]

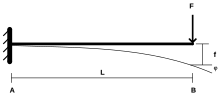
오일러-베르누이 보 방정식

공학적 점하중(f)에서 캔틸레버의 편향

오일러-베르누엘리 빔 방정식은 빔 요소의 동작을 정의한다(아래 참조). 이는 다음 5가지 가정을 기반으로 한다.

연속체 역학은 벤딩 빔에 유효하다.
단면에서의 응력은 벤딩 방향에서 선형적으로 변화하며, 모든 단면 중심에서 0이다.
특정 단면에서의 벤딩 모멘트는 해당 위치에서 비껴진 형상의 두 번째 파생 모델에 따라 선형적으로 변화한다.
빔은 등방성 물질로 구성된다.
적용된 하중은 빔의 중립 축과 직교하며 고유한 평면에서 작용한다.

오일러-베르누엘리 빔 방정식의 단순화된 버전은 다음과 같다.

{\dx^{d^{2}}:{dx^{2}}:}\좌측(EI{\frac {d^{2}w}{dx^{d^{2}w}{dx^{2}}}\오른쪽)=q(x)=\,}

여기서 $w$ $w$ 은 $w$ (는) 편향이고 $q(x)$ ) $q(x)$ 은 $q(x)$ 단위 길이당 부하다. $E$ $E$ 은 $E$ 탄성계수이고 $I$ $I$ 은 면적의 두 번째 순간으로 $I$ , 빔의 휨강성을 제공하는 이들의 산물이다.

이 방정식은 공학적 실무에서 매우 일반적이다: 균일한 정적 빔의 편향을 설명한다.

$w$ $w$ 의 연속적인 파생상품은 다음과 같은 중요한 의미를 갖는다 $w$ .

$\textstyle {w}\,$ $displaystyle \textstyle {w}\,}$ 이(가) 편향이다 $\textstyle {w}\,$ .

$\textstyle {\frac {dw}{dx}}\,$ $\textstyle {\frac {dw}{dx}}\,$ $\textstyle {\frac {dw}{dx}}\,$ $displaystyle \textstyle {\frac {frac}{dx}\,}$ 은 $\textstyle {\frac {dw}{dx}}\,$ (는) 빔의 기울기다.

$\textstyle {-EI{\frac {d^{2}w}{dx^{2}}}}\,$ $\textstyle {-EI{\frac {d^{2}w}{dx^{2}}}}\,$ $\textstyle {-EI{\frac {d^{2}w}{dx^{2}}}}\,$ $\textstyle {-EI{\frac {d^{2}w}{dx^{2}}}}\,$ $\textstyle {-EI{\frac {d^{2}w}{dx^{2}}}}\,$ w $\textstyle {-EI{\frac {d^{2}w}{dx^{2}}}}\,$ $\textstyle {-EI{\frac {d^{2}w}{dx^{2}}}}\,$ $displaystyle \textstyle {-EI{\frac {d^{2}w}{dx^{2}}\,}}$ 는 $\textstyle {-EI{\frac {d^{2}w}{dx^{2}}}}\,$ 빔의 벤딩 모멘트다.

$\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ $\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ $\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ ( $\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ $\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ d $\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ $\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ $\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ $\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ 2 $\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ ) $dstyle \textstyle {-{\frac {d}{dx}}}\좌측(EI{\frac$ {d $^{d^{$ 2} $w}{dx^{2}}}\,}},}}$ 은(는) 빔의 전단력이다 $\textstyle {-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}\,$ .

휨모멘트는 긴장력과 압축력으로 나타나며, 보에서 부부 역할을 한다. 이러한 힘에 의해 발생하는 스트레스는 다음과 같이 나타낼 수 있다.

\sigma ={\frac {My}{I}}=-Ey{\frac {d^{2}w}{dx^{2}},},

여기서 $\sigma$ ${\displaystyle \sigma$ }은 $\sigma$ $($ 는) $응력$ 이고, M {\ $displaystyle$ M}은 $M$ (는 $)$ $벤딩$ 모멘트, y {\displaystyle $y}$ 은 $y$ (는) 빔의 중립 축에서 고려 중인 $지점까지의 거리,$ I ${\$ displaystystyle I}은 $I$ 면적의 두 번째 모멘트다. $I/y$ 방정식은 $I/y$ 계수 $S$ ${\$ $displaystyle S}$ 로 나눈 순간으로 단순화된다 $I/y$ 이 방정식은 구조 엔지니어가 휨 모멘트에 노출되었을 때 구조 요소의 응력을 평가할 수 있게 한다.

버클링

좌굴의 특성 변형을 나타내는 중심 축하중 아래의 기둥.

압축력에 노출될 경우 하중물의 불안정 효과로 인해 구조적 요소가 크게 변형될 수 있다. 그 효과는 제조나 건설의 부정확성으로 인해 시작되거나 악화될 수 있다.

오일러 좌굴 공식은 스트럿(또는 칼럼)이 좌굴에서 고장을 일으키는 축압력을 정의한다.

{\displaystyle F={\frac {\pi ^{2}EI}{(Kl)^{2}}:

어디에

F

F

F

= 최대 또는 임계 힘(기둥의 수직 하중),

E

E

E

= 탄성 계수,

I

I

I

= 영역 모멘트 관성 또는 두 번째 영역 모멘트

l

l

l

= 지원되지 않는 열 길이,

K

K

K

= 컬럼 유효 길이 계수, 이 값은 다음과 같이 컬럼의 엔드 지지 조건에 따라 달라진다.

핀으로 고정된(힌딩된, 회전할 수 있는 자유),

K

K

K

= 1.0.

양쪽 끝이 고정된 경우

K

K

K

= 0.50.

한쪽 끝이 고정되고 다른 쪽 끝이 고정된 경우

K\approx

≈

K\

약 0.70

K\approx

.

한 쪽 끝을 고정하고 다른 쪽 끝을 자유롭게 횡방향으로 이동할 수 있는

경우

K

{\displaystyle

K}

K

= 2.0.

이 값은 때로 설계 목적으로 임계좌굴 응력으로 표현된다.

{\displaystyle \sigma ={\frac {\pi^{2}E}{{\frac {Kl}{r}}^{2}}:

어디에

\sigma

\sigma

\sigma

= 최대 또는 임계 응력

r

[\displaystyle r}

r

= 횡단면의 최소 회전 반지름

다른 형태의 버클링에는 벤딩 시 빔의 압축 플랜지가 버클링되는 측면 비틀림 버클링과 플레이트 평면의 압착으로 인한 플레이트 거더의 판 요소 버클링이 있다.

참고 항목

참조

^ Melchers, R. E. (2002), “Structural Reliability Analysis and Prediction,” 2nd Ed., John Wiley, Chichester, UK.
^ Piryonesi, Sayed Madeh; Tavakolan, Mehdi (9 January 2017). "A mathematical programming model for solving cost-safety optimization (CSO) problems in the maintenance of structures". KSCE Journal of Civil Engineering. 21 (6): 2226–2234. doi:10.1007/s12205-017-0531-z.
^ Dym, Clive L. (1997). Structural Modeling and Analysis. Cambridge University Press. p. 98. ISBN 0-521-49536-9.
^ Heyman, Jacques (1998). Structural Analysis: A Historical Approach. Cambridge University Press. ISBN 0-521-62249-2.
^ Nilson, Arthur H.; Darwin, David; Dolan, Charles W. (2004). Design of Concrete Structures. McGraw-Hill Professional. p. 486. ISBN 0-07-248305-9.
^ Heyman, Jacques (1999). The Science of Structural Engineering. Imperial College Press. ISBN 1-86094-189-3.

카스티글리아노, 카를로 알베르토(번역기: 앤드류스, 유와트 S. (1966년). 탄성계통의 평형론과 그 응용에 관한 연구 도버 출판물
Dym, Clive L. (1997) 구조 모델링 및 분석. 케임브리지 대학 출판부. ISBN 0-521-49536-9
듀가스, 르네(1988) 역학의 역사. Courier Dover Publishes. ISBN 0-486-65632-2
휴슨, 나이젤 R. (2003) 프리스트레스트 콘크리트 교량: 설계 및 시공. 토마스 텔포드 ISBN 0-7277-2774-5
헤이먼, 자크(1998) 구조 분석: 역사적 접근법. 케임브리지 대학 출판부. ISBN 0-521-62249-2
헤이먼, 자크(1999년). 구조 공학의 과학. 임페리얼 칼리지 프레스. ISBN 1-86094-189-3
Hogogestad, E. 철근콘크리트 부재의 휨과 축하중의 조합에 관한 연구 일리노이 대학교 엔지니어링 실험 스테이션, 게시판 시리즈 N.399
제닝스, 앨런(2004) 구조: 이론에서 실천으로. 테일러 & 프랜시스 ISBN 978-0-415-26843-1
레온하르트, A. (1964) Caementum zum Spannbeton, 밴드 III(시멘트부터 프리스트레스트 콘크리트까지). 바우버랙 GmbH.
맥닐, 리처드 H. (1994년). 유한 요소: 설계 및 성능. 마르셀 데커 ISBN 0-8247-9162-2.
뫼르쉬, E. (Stuttgart, 1908). Der Eisenbetonbau, Seine Theri und Anwendung, (보강 콘크리트 구조, 그 이론과 적용) 콘래드 비트워어, 제3판
Nedwell, P.J.; Molly, R.N. (ed) (1994년) 강하:제5차 국제 심포지엄의 진행. 테일러 & 프랜시스 ISBN 0-419-19700-1
뉴턴, 아이작, 레서, 토마스, 재키어, 프랑수아(1822년) Philosphious Naturalis Principia Mathematica. 옥스퍼드 대학교
닐슨, 아서 H.; 다윈, 데이비드; 돌란, 찰스 W. (2004) 콘크리트 구조물의 설계. 맥그로힐 프로페셔널 ISBN 0-07-248305-9
로잔스카야, 마리암, 레비노바, I. S. (1996년) 모렐론, 레기스 & 라쉬드, 로슈디(1996년)의 "통계학" 아랍 과학사 백과사전, 2-3권, Routrege. ISBN 0-415-02063-8
Schlaich, J, K. Shafer, M. Jennewein (1987년) "구조 콘크리트의 일관성 있는 설계"를 참조하십시오. PCI 저널, 특별 보고서, 32권, 3호.
스콧, 리처드(2001) Tacoma의 Wake of Tacoma: 서스펜션 브리지와 공기역학적 안정성을 위한 탐색 ASCE 간행물. ISBN 0-7844-0542-5.
Turner, J.; Clough, R.W.; Martin, H.C.; 토프, 엘제이(1956) "복합 구조물의 강도와 처짐" 항공 과학 저널 23호.
K.S. 비르디(2000년) 구조물에 대한 비정상적 하중: 실험 및 수치 모델링. 테일러 & 프랜시스 ISBN 0-419-25960-0

[:0-1] Melchers, R. E. (2002), “Structural Reliability Analysis and Prediction,” 2nd Ed., John Wiley, Chichester, UK.

[:1-2] Piryonesi, Sayed Madeh; Tavakolan, Mehdi (9 January 2017). "A mathematical programming model for solving cost-safety optimization (CSO) problems in the maintenance of structures". KSCE Journal of Civil Engineering. 21 (6): 2226–2234. doi:10.1007/s12205-017-0531-z.

[3] Dym, Clive L. (1997). Structural Modeling and Analysis. Cambridge University Press. p. 98. ISBN 0-521-49536-9.

[Heyman1-4] Heyman, Jacques (1998). Structural Analysis: A Historical Approach. Cambridge University Press. ISBN 0-521-62249-2.

[5] Nilson, Arthur H.; Darwin, David; Dolan, Charles W. (2004). Design of Concrete Structures. McGraw-Hill Professional. p. 486. ISBN 0-07-248305-9.

[Heyman-6] Heyman, Jacques (1999). The Science of Structural Engineering. Imperial College Press. ISBN 1-86094-189-3.

[1]

[2]

[3]

[4]

[5]

[6]

Search