삼원 플롯

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 찾기 : "Ternary Plot" – 뉴스 · 신문 · 서적 · 학자 · JSTOR (2014년 1월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

삼원 그림, 삼원 그래프, 삼각 그림, 심플렉스 그림, 깁스 삼각형 또는 드 피네티 다이어그램은 상수를 ^[1]합한 세 변수에 대한 중심 그림이다.이 그림에서는 세 변수의 비율을 정삼각형의 위치로 그래픽으로 표현합니다.그것은 물리 화학, 암석학, 광물학, 야금학, 그리고 다른 물리 과학에서 세 가지 종으로 구성된 시스템의 구성을 보여주기 위해 사용됩니다.집단 유전학에서 유전자형 빈도의 삼각형 그림을 드 피네티 다이어그램이라고 합니다.게임 이론에서, 그것은 종종 단순 ^[2]플롯이라고 불린다.삼원 그림은 3차원 사례에서 구성 데이터를 분석하는 도구입니다.

삼원 그림에서 세 변수 a, b 및 c의 값은 일정한 상수 K로 합해야 합니다.일반적으로 이 상수는 1.0 또는 100%로 표시됩니다.그래프화되는 모든 물질에 대해 a + b + c = K이므로 한 변수는 다른 변수와 독립적이지 않으므로 그래프에서 표본의 점을 찾으려면 두 변수만 알고 있어야 합니다. 예를 들어, c는 K - a - b와 같아야 합니다.세 가지 수치들은 독립적으로 변할 수 없기 때문에, 자유도는 두 가지뿐이므로, 두 가지 차원에서만 세 변수의 조합을 그래프로 표시할 수 있다.

화학조성을 묘사하기 위해 3원 그림을 사용하는 것의 장점은 3개의 변수를 2차원 그래프에 편리하게 표시할 수 있다는 것이다.3원 그림을 사용하여 여러 위상이 존재하는 그래프에 합성 영역을 윤곽화하여 위상 다이어그램을 작성할 수도 있습니다.

삼원 그림에서 점의 값은 삼원 좌표 또는 중심 좌표에 대응합니다(최대 상수).

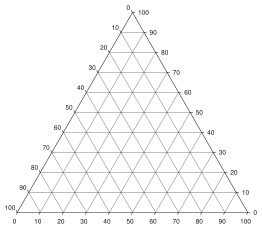
삼원 그림에서 값 읽기

그림에서 점의 값을 결정하는 데 사용할 수 있는 세 가지 동등한 방법이 있습니다.

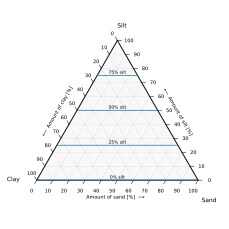
1. 평행선 또는 그리드 방식.첫 번째 방법은 삼각형 모서리에 평행한 선으로 구성된 다이어그램 그리드를 사용하는 것입니다.삼각형의 변에 대한 평행선은 변과 반대되는 정점에 위치한 성분의 점 상수 궤적입니다.각 구성요소는 삼각형의 한 구석에 100%, 반대쪽 모서리에 0%가 있으며, 이 모서리로부터의 거리(반대쪽 모서리에 수직)가 증가함에 따라 선형적으로 감소합니다.제로선과 코너 사이에 일정한 간격으로 평행선을 긋는 것으로, 추정하기 쉬운 미세한 분할을 확립할 수 있다.
2. 수직선 또는 고도법.그리드 선이 없는 다이어그램의 경우, 값을 결정하는 가장 쉬운 방법은 관심 지점에서 세 변 각각까지의 최단 거리(즉, 수직)를 결정하는 것이다.비비아니의 정리에 따르면 거리(또는 삼각형 높이에 대한 거리의 비율)는 각 성분의 값을 제공합니다.
3. 코너 라인 또는 교차 방식.세 번째 방법에서는 수직선이나 평행선을 그릴 필요가 없습니다.각 모서리에서 관심점을 지나 삼각형의 반대쪽으로 직선이 그려집니다.이러한 선의 길이는 점과 해당 변 사이의 세그먼트 길이와 함께 개별적으로 측정됩니다.그런 다음 측정된 선의 비율은 성분 값을 100%의 비율로 제공합니다.

평행선(그리드선)에 따른 변위는 2개의 값의 합을 유지하는 반면 수직선을 따른 움직임은 3번째 값의 감소(증가)의 각각 절반씩 2개의 값을 증가(또는 감소)시킨다.모서리를 통과하는 선을 따라 이동하면 다른 두 값의 비율이 유지됩니다.

• 

  그림 1고도법

• 

  그림 2교차법

• 

  그림 3점이 표시되지 않은 삼원 다이어그램 예제입니다.

• 

  그림 4첫 번째 축에 따른 증분을 보여주는 삼원 다이어그램의 예입니다.

• 

  그림 5두 번째 축을 따른 증분을 보여주는 삼원 다이어그램의 예입니다.

• 

  그림 6세 번째 축에 따른 증분을 보여주는 삼원 다이어그램의 예입니다.

• 

  그림 7빈 삼원 그림

• 

  그림 8세 축의 작동 방식을 나타냅니다.

• 

  주 그리드 선이 있는 레이블이 없는 삼각형 그림

• 

  주 격자선과 보조 격자선이 있는 레이블이 없는 삼각형 그림

데카르트 좌표로부터의 도출

데카르트 좌표에서 삼원도의 도출

그림 (1)은 축 a, b, c를 각각 갖는 3차원 데카르트 공간에서의 점 P(a, b, c)의 경사 투영을 나타낸다.

a + b + c = K(양수), P는 A(K,0,0), B(0,K,0) 및 C(0,0,K)를 포함하는 평면으로 제한됩니다.a, b, c 각각이 음수일 수 없는 경우, P는 (2)와 같이 A, B, C로 둘러싸인 삼각형으로 제한된다.

(3)에서는 축을 회전시켜 등각도를 제공한다.그 삼각형은 정면으로 보면 등변으로 보인다.

(4)에서 선 BC, AC, AB로부터의 P의 거리를 각각 a,, b and, c,로 나타낸다.

벡터 형태(nθ는 단위 벡터) 및 점 p의 모든 선 l = s + t nθ에 대하여, p에서 l까지의 수직 거리는 다음과 같다.

$\displaystyle \left \(\mathbf {s} -\mathbf {p} )-{\bigl(\mathbf {s} -\mathbf {p})\cdot \mathbf {n} \mathbf {n} \right\\,}$

이 경우 P점은

$(\displaystyle \mathbf {p} = pmatrix a\b\c\end{pmatrix}),}$

회선 BC는

${\displaystyle \mathbf {s} =begin {pmatrix} 0\K\\\end {pmatrix}\quad {text {and}}\mathbf {n} =begin {pmatrix} 0\K\end {pmatrix}\K}+{(-K)}^{2}}}={begin{pmatrix}0\{\frac {1}{\frac {1}{\fracrt {2}}\end{pmatrix},}$

수직 거리 공식을 사용하여

$({displaystyle {pmatrix}-a\K-b\c\end{pmatrix}-\left({\begin{pmatrix}-a\K-b\c\end{pmatrix}\cdot {pmatrix}\{\frac1-rt2})=\left\{begin{pmatrix}-a\K-b\\c\end{pmatrix}-\left(0+{\frac {K-b}{\sqrt {2}}+{\frac {c}{\rt {2}}\right}{\frac{pmatrix}}}{\frt}{\frt}}}{\frt}}}}{\frt{\frt}}}}}}}}{\frt{\frt}}}}}}}}=\left\{begin{pmatrix}-a\K-b-{\frac {K-b+c}{2}\c+{\frac {K-b+c}{2}}}\end {pmatrix}\right =\left\{\frac {K-b-c}{2}\{\frac {K-b-c}{2}\end {pmatrix}\right\[10px]&= sqrt { { （ - a ） }^2} + { \ leftflac { K - b - c } {2} } \ right )}^{2}+{\left({\frac {K-b-c}{2}}\오른쪽)}^{2}}=sqrt {a^{2}+{\frac{(K-b-c)}{2}}{2}}}}},\end { aligned}}$

K = a + b + c로 치환하면,

${{displaystyle a'=paramrt {a^{2}+{\frac {a+b-c)}{2}}}}=paramrt {a^{2}+{\frac {a^{2}}}}=paramrt {frac {3}{2}},}$

AC 및 AB 라인에 대한 유사한 계산이 제공됨

${\displaystyle b'=bfrac {3}{2}}\text {and}\display c'=cfrac {3}{2},}$

이는 각 선에서 점의 거리가 원래 값 a, b 및 ^[3]c에 선형적으로 비례함을 나타냅니다.

삼원 플롯 그리기

데카르트 좌표는 삼각형의 점을 그리는 데 유용합니다.a = 100%가 (x,y) = (0,0)에 배치되고 b = 100%가 (1,0)에 배치되는 등변 삼원 그림을 고려합니다.다음으로 c = 100%는 ($\frac{1}{}2\frac{\sqrt{\mathrm{}}}{}$ ,$\frac{\mathrm{}}{}$ 2 $),$ {\$textstyle({\frac {$1}{2$}}, {\frac {\frac {3}}}{$2$\}\}),$ 트리플$$(a,b,c)은 다음과 같습니다.

$\displaystyle \frac {1}{2}}\cdot {frac {2b+c}{a+b+c}, {\frac {3}{2}}\cdot {frac {c}{a+b+c}\right},}$

예

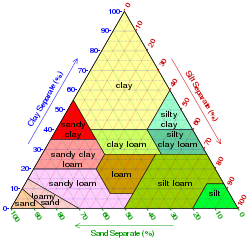
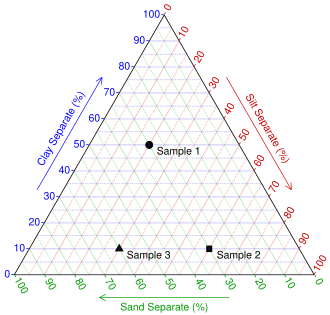
다음 예시는 3개의 토양 샘플로 구성된 가상 세트에 대해 어떻게 작동하는지를 보여 줍니다.

샘플	점토	실트	모래	메모들
샘플 1	50%	20%	30%	점토와 실트가 이 샘플의 70%를 차지하기 때문에 성분이 100%가 되려면 모래의 비율이 30%여야 합니다.
샘플 2	10%	60%	30%	모래의 비율은 시료 1과 같이 30%이지만, 실트 비율이 40% 증가하면 그에 따라 점토의 비율도 감소한다.
샘플 3	10%	30%	60%	이 표본은 점토의 비율은 표본 2와 동일하지만, 침적토와 모래의 비율은 서로 바뀌었습니다. 그래프는 수직 축을 기준으로 반영됩니다.

점 그리기

• 

  Plotting Sample 1 (1) : 50% 점토선 찾기

• 

  플롯 샘플 1 (2): 20% 실트 라인 찾기

• 

  그림 샘플 1(3):교차점은 처음 두 개의 모래 선에 수학적으로 의존하기 때문에 30% 모래 선과 일치합니다.

• 

  모든 샘플 플롯

주목할 만한 삼원도 목록

• 색도
• 피네티 도표
• 달리츠 플롯
• 가연성도
• 옌센 양이온 그림
• 수화학에 사용되는 파이퍼 다이어그램
• QFL 다이어그램
• QAPF 다이어그램
• 초산암 분류도

「 」를 참조해 주세요.

• 겉보기 어금니
• 비비아니의 정리
• 중심 좌표(수학)
• 구성 데이터
• 정보 그래픽스 소프트웨어 목록
  • 지구과학 그래픽스 소프트웨어
  • IGOR Pro
  • 오리진(데이터 분석 소프트웨어)
  • R은 Comprehensive R Archive Network(CRAN; 종합 R 아카이브 네트워크)에 전용 패키지 3진수를 보유하고 있습니다.
  • 시그마플로트
• 프로젝트 삼각형
• 트릴레마

레퍼런스

외부 링크

• "Excel Template for Ternary Diagrams". serc.carleton.edu. Science Education Resource Center (SERC) Carleton College. Retrieved 14 May 2020.
• "Tri-plot: Ternary diagram plotting software". www.lboro.ac.uk. Loughborough University – Department of Geography / Resources Gateway home > Tri-plot. Retrieved 14 May 2020.
• "Ternary Plot Generator – Quickly create ternary diagrams on line". www.ternaryplot.com. Retrieved 14 May 2020.
• Holland, Steven (2016). "Data Analysis in the Geosciences – Ternary Diagrams developed in the R language". strata.uga.edu. University of Georgia. Retrieved 14 May 2020.