플롯(그래픽)

Plot (graphics)
올드 페이스풀 분출 간격 산점도(온천)

플롯은 데이터 집합을 나타내는 그래픽 기법이며, 일반적으로 두 개 이상의 변수 간의 관계를 보여 주는 그래프로 표시됩니다.플롯은 손으로 그리거나 컴퓨터로 그릴 수 있다.과거에는 기계식 또는 전자식 플롯터가 사용되기도 했다.그래프는 변수 간의 관계를 시각적으로 표현한 것으로, 값 목록에서 나오지 않을 수 있는 이해를 신속하게 도출할 수 있는 인간에게 매우 유용하다.척도 또는 눈금자가 주어진 경우 그래프를 사용하여 알려진 변수의 함수로 표시된 미지의 변수 값을 읽을 수도 있지만, 이는 표 형식으로 표시된 데이터로도 수행할 수 있습니다.함수 그래프는 수학, 과학, 공학, 기술, 금융 및 기타 분야에서 사용됩니다.

개요

그래프는 통계량과 데이터 분석에서 중요한 역할을 합니다.여기서의 순서는 크게 양적 부분과 그래픽 부분 두 가지로 나눌 수 있습니다.정량적 기법은 숫자 또는 표 형식의 출력을 산출하는 일련의 통계 절차입니다.정량적 기법의 예는 다음과 같다.[1]

이러한 기술들과 유사한 기술들은 모두 가치가 있고 고전적인 분석의 관점에서 주류이다.일반적으로 그래픽 기법이라고 불리는 통계 도구도 많이 있습니다.여기에는 다음이 포함됩니다.[1]

그래프와 같은 그래픽 절차는 검정 가정, 모형 선택, 모형 검증, 추정기 선택, 관계 식별, 요인 효과 결정, 특이치 탐지 등의 측면에서 데이터 세트에 대한 통찰력을 얻는 짧은 방법입니다.통계 그래픽은 데이터의 [1]기본 구조에 대한 통찰력을 제공합니다.

그래프는 일반적으로 두 그림이 교차하는 위치를 찾아 일부 수학 방정식을 푸는 데도 사용할 수 있습니다.

플롯의 종류

다음 항목도 참조하십시오.공통:카테고리:유형별 그림
  • 점도 : 통계량에 사용되는 그래프 유형입니다.점도표를 사용하면 데이터 행렬의 표본과 변수에 대한 정보를 그래픽으로 표시할 수 있습니다.샘플은 점으로 표시되고 변수는 벡터, 선형 축 또는 비선형 궤적으로 표시됩니다.범주형 변수의 경우 범주 수준 점을 사용하여 범주 변수의 수준을 나타낼 수 있습니다.일반화 비점도에는 연속형 및 범주형 변수에 대한 정보가 표시됩니다.
  • Bland-Altman 플롯 : 분석 화학 및 생물 통계학에서 이 플롯은 두 가지 다른 분석 간의 합치 분석에 사용되는 데이터 플롯의 방법입니다.이는 다른 분야에서 여전히 알려진 Tukey 평균-차이 그림과 동일하지만, Bland와 [2][3]Altman에 의해 의료 통계에서 대중화되었다.
  • 신호도는 제어 이론에서 사용됩니다.
  • 상자 그림 : 설명 통계량에서 상자-수염 다이어그램 또는 그림이라고도 하는 상자 그림은 5개의 숫자 요약(가장 작은 관측치, 하위 사분위수(Q1), 중위수(Q2), 상위 사분위수(Q3) 및 가장 큰 관측치)를 통해 숫자 데이터 그룹을 그래픽으로 표현하는 편리한 방법입니다.상자 그림은 특이치로 간주될 수 있는 관측치가 있는 경우 이를 나타낼 수도 있습니다.
  • 카펫 그림 : 2-3개의 독립 변수와 1-3개의 종속 변수 사이의 교호작용을 나타내는 2차원 그림입니다.
  • 혜성 플롯 : 데이터 포인트가 화면에서 추적되는 2차원 또는 3차원 애니메이션 플롯.
  • 등고선도 : 표시된 수량 q가 상수인 등고선이라고 하는 1차원 곡선을 보여주는 2차원 그림입니다.임의로 플롯된 값을 컬러 코딩할 수 있습니다.
  • Dalitz 그림 : 입자 물리학에서 종종 사용되는 산점도이며, 특정(비슷한) 삼체 붕괴의 산물이 서로 떨어질 수 있는 다양한(운동학적으로 구별되는) 방식의 상대적 빈도를 나타냅니다.
  • 깔때기 그림 : 메타분석에서 출판편향이 존재하는지 확인하기 위해 고안된 유용한 그래프입니다.1994년[5] Light와 Pillemer에 의해 도입되고 Egger와 [6]동료들에 의해 자세히 논의된 깔때기 플롯은 메타 분석의 유용한 부가물이다.깔때기 그림은 연구 크기의 측정값에 대한 처리 효과의 산점도입니다.이는 주로 편향 또는 체계적인 이질성을 감지하는 시각적인 보조 도구로 사용됩니다.
  • 도트 그림(통계량): 도트 차트 또는 도트 그림은 단순 척도로 표시된 데이터 점의 그룹으로 구성된 통계 차트입니다.점 그림은 연속형, 양적, 일변량 데이터에 사용됩니다.데이터 포인트가 적으면 라벨을 붙일 수 있습니다.점 그림은 사용할 수 있는 가장 간단한 그림 중 하나이며 작고 중간 크기의 데이터 세트에 적합합니다.특이치뿐만 아니라 군집과 간격을 강조 표시하는 데 유용합니다.
  • 포레스트 플롯 : 정량적 과학 연구에서 증거의 강도를 보여주는 그래픽 표시입니다.무작위 대조 실험 결과의 메타 분석을 그래픽으로 표현하는 수단으로 의학 연구에 사용하기 위해 개발되었다.지난 20년 동안, 유사한 메타 분석 기법이 관찰 연구(예: 환경 역학)에 적용되었고 숲 그림도 그러한 연구의 결과를 제시하는 데 종종 사용된다.
  • 갤브레이스 그림 : 통계학에서 갤브레이스 그림(갤브레이스의 반지름 그림 또는 단순히 반지름 그림이라고도 함)은 서로 다른 표준 [7]오차를 가진 동일한 양의 여러 추정치를 표시하는 한 방법입니다.포레스트 플롯의 대안 또는 보충물로 메타 분석에서 이질성을 검토하는 데 사용할 수 있다.
  • 히트 맵
  • 롤리팝 그림
  • 니콜스 플롯 : 직교축의 주파수 응답 위상에 대해 진폭의 로그가 플롯되는 신호 처리에 사용되는 그래프입니다.
  • 정규 확률도 : 정규 확률도는 데이터 집합이 근사적으로 정규 분포를 따르는지 여부를 평가하기 위한 그래픽 기법입니다.데이터는 점들이 근사 직선을 형성하도록 이론적 정규 분포를 기준으로 표시됩니다.이 직선으로부터의 이탈은 정규성으로부터의 이탈을 나타냅니다.정규 확률도는 확률도의 특수한 경우입니다.
  • 나이키스트 그림 : 자동 제어 및 신호 처리에 사용되어 피드백이 있는 시스템의 안정성을 평가합니다.이 그래프는 주파수 응답의 게인과 위상이 표시된 극좌표 그래프로 표시됩니다.이러한 위상 수량의 그래프는 위상을 각도로, 크기를 원점으로부터의 거리로 표시합니다.
  • 부분 회귀 그림 : 적용된 통계량에서 부분 회귀 그림은 모형에 다른 변수를 추가하는 효과를 보여주려고 합니다(하나 이상의 독립 변수가 모형에 이미 있는 경우).부분 회귀 그림은 추가된 변수 그림, 수정된 변수 그림 및 개별 계수 그림이라고도 합니다.
  • 부분 잔차 그림 : 적용된 통계량에서 부분 잔차 그림은 주어진 독립 변수와 반응 변수 사이의 관계를 보여 주는 그래픽 기법입니다. 다른 독립 변수도 모형에 있습니다.
  • 확률도 : 확률도는 데이터 집합이 정규 분포 또는 Weibull과 같은 주어진 분포를 따르는지 여부를 평가하고 선택한 분포의 위치 및 척도 모수를 시각적으로 추정하기 위한 그래픽 기법입니다.데이터는 점들이 거의 직선을 형성하도록 이론적 분포에 대해 표시됩니다.이 직선으로부터의 출발은 지정된 분포로부터의 출발을 나타냅니다.
  • Q–Q 그림 : 통계에서 Q–Q 그림(Q는 분위수를 나타냄)은 랜덤 표본을 추출한 통계 모집단의 확률 분포와 비교 분포 간의 차이를 진단하는 그래픽 방법입니다.검정할 수 있는 차이의 예로는 모집단 분포의 비정규성이 있습니다.
  • 반복도 : 기술통계학 및 카오스 이론에서 반복도(RP)는 특정 시점의 위상공간 시간을 나타내는 그림입니다.바꿔 말하면, 그것은 의 그래프이다.
수평 축에 i i를 하고 수직 축에j(\ j를 표시합니다. 서 x {\은 위상 공간 궤적입니다.
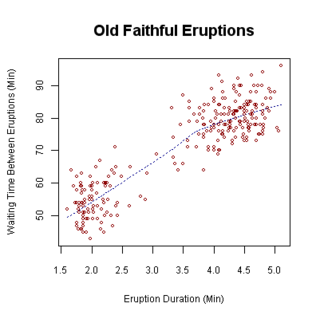
  • 산점도 : 산점도 또는 산점도란 데이터 집합에 변수를 사용하는 표시 유형입니다.데이터는 점의 집합으로 표시되며, 각각은 수평 축의 위치를 결정하는 한 변수의 값과 수직 [8]축의 위치를 결정하는 다른 변수의 값을 가집니다.
  • 슈무 플롯 : 전기공학에서 슈무 플롯은 다양한 조건과 입력에 따라 변화하는 성분 또는 시스템의 반응을 그래픽으로 표시하는 것입니다.컴퓨터, ASIC, 마이크로프로세서 등 복잡한 전자 시스템의 테스트 결과를 나타내는 데 자주 사용됩니다.그림에는 일반적으로 테스트 대상 장치가 작동하는 조건의 범위가 표시됩니다.
  • 스파게티 그림은 시스템을 통과하는 가능한 흐름을 시각화하기 위해 데이터를 보는 방법입니다.이렇게 묘사된 흐름은 국수처럼 나타나기 때문에 이 [9]용어의 결합이다.이 통계 방법은 처음에 공장에서의 루팅을 추적하기 위해 사용되었습니다.이러한 방법으로 플로우를 시각화하면 시스템 플로우 내의 비효율성을 줄일 수 있습니다.
  • 줄기 그림 : 통계학에서 줄기 그림(또는 줄기-잎 그림)은 분포의 모양을 시각화하는 데 도움이 되도록 히스토그램과 유사한 그래픽 형식으로 정량적 데이터를 표시하는 장치입니다.그것들은 1900년대 초 Arthur Bowley의 작품에서 발전하여 탐색적 데이터 분석에 유용한 도구입니다.히스토그램과 달리 스템플롯은 원본 데이터를 적어도 두 개의 유효 자릿수로 유지하고 데이터를 순서대로 배치함으로써 순서 기반 추론 및 비모수 통계로 쉽게 이동할 수 있습니다.
  • 별 그림 : 다변량 데이터를 표시하는 그래픽 방법입니다.각 별은 하나의 관측치를 나타냅니다.일반적으로 별 그림은 각 페이지에 여러 개의 별이 있고 각 별은 하나의 관측치를 나타내는 다중구 형식으로 생성됩니다.
  • 표면도 : 이 그래프 유형에서 표면도는 데이터 세쌍둥이(X,Y,Z) 집합에 적합하도록 표시됩니다. 여기서 Z는 표시할 함수로 구할 경우 Z=f(X,Y)입니다.일반적으로 X와 Y 값의 집합은 동일한 간격으로 배치됩니다.임의로 플롯된 값을 컬러 코딩할 수 있습니다.
  • 삼원 그림: 삼원 그림, 삼원 그래프, 삼각 그림, 심플렉스 그림 또는 드 피네티 다이어그램은 상수를 합한 세 변수의 2원 중심 그림입니다.이 그림에서는 세 변수의 비율을 정삼각형의 위치로 그래픽으로 표현합니다.그것은 암석학, 광물학, 야금학, 그리고 다른 물리 과학에서 세 가지 종으로 구성된 시스템의 구성을 보여주기 위해 사용된다.집단 유전학에서는 종종 드 피네티 도표로 불린다.게임 이론에서, 그것은 종종 단순 플롯이라고 불린다.
  • 벡터장 : 벡터장 그림(또는 진동도)은 2D 또는 3D 점과 관련된 벡터의 방향과 강도를 나타냅니다.일반적으로 평면 또는 표면적에 대한 그라데이션 강도를 표시하는 데 사용됩니다.
  • 바이올린 플롯: 바이올린 플롯은 숫자 데이터를 표시하는 방법입니다.또한 서로 다른 값(가장 간단한 경우 히스토그램일 수 있음)에서 데이터의 확률 밀도를 보여준다는 점을 제외하면 상자 그림과 유사합니다.일반적으로 바이올린 그림에는 표준 상자 그림에서처럼 데이터의 중위수에 대한 마커와 사분위 간 범위를 나타내는 상자가 포함됩니다.이 상자 그림에는 커널 밀도 추정치가 중첩되어 있습니다.바이올린 플롯은 Vioplot 라이브러리를 통한 R과 Vioplot 애드인을 [10]통한 Stata를 포함한 많은 소프트웨어 패키지의 확장으로 사용할 수 있습니다.

특정 수량에 대한 그림

  • Arrhenius 그림 : 이 그림은 반온도(1/ \1abscissa)에 대해 표시된 반응속도((k ) \( k ), 좌표축)의 로그를 비교합니다.아레니우스 그림은 화학 반응 속도에 대한 온도의 영향을 분석하는 데 자주 사용됩니다.
  • 도트 플롯(생물정보학) : 이 플롯은 두 생물학적 염기서열을 비교하며, 이들 사이의 유사성이 매우 높은 영역을 식별할 수 있는 그래픽 방법입니다.그것은 일종의 반복 플롯이다.
  • Lineweaver-Burk 그림 : 이 그림은 반응 속도와 기질 농도의 상호 작용을 비교합니다.그것은 효소 동역학을 나타내고 결정하는 데 사용된다.

3D 플롯

예

그래프의 종류와 용도는 매우 다양하다.대표적인 예는 다음과 같습니다.

  • 심플 그래프: 공급과 수요의 곡선, 경제학에서 공급과 수요를 가격과 관련짓기 위해 사용되는 심플 그래프.그래프를 함께 사용하여 경제적 균형을 결정할 수 있다(기본적으로 방정식을 풀기 위해).
  • 값을 읽는 데 사용되는 간단한 그래프: 예를 들어 성인 남성 모집단에 대한 데이터가 주어지면 남성의 키가 특정 범위에 있을 확률을 도출할 수 있는 종 모양의 정규 분포 또는 가우스 확률 분포.
  • 매우 복잡한 그래프: 온도, 압력, 습도 및 기타 양에 관한 심리 측정 차트.
  • 비직사각형 좌표: 위의 모든 것은 2차원 직사각형 좌표를 사용합니다. 극좌표를 사용하는 그래프의 예로는 특정 유형의 안테나가 모든 방향으로 방사하는 전력을 나타내는 안테나 방사 패턴 도표가 있습니다.

「 」를 참조해 주세요.

레퍼런스

Public Domain이 문서에는 미국 국립표준기술연구소 웹사이트 https://www.nist.gov의 퍼블릭 도메인 자료가 포함되어 있습니다.

  1. ^ a b c NIST/SEMATECH(2003)"그래픽의 역할"인: 2003년 1월 6일 통계방법 전자수첩(작성일).
  2. ^ Altman DG, Bland JM (1983). "Measurement in medicine: the analysis of method comparison studies". The Statistician. Blackwell Publishing. 32 (3): 307–317. doi:10.2307/2987937. JSTOR 2987937.
  3. ^ Bland JM, Altman DG (1986). "Statistical methods for assessing agreement between two methods of clinical measurement". Lancet. 1 (8476): 307–10. doi:10.1016/S0140-6736(86)90837-8. PMID 2868172. S2CID 2844897.
  4. ^ a b Simionescu, P.A. (2014). Computer Aided Graphing and Simulation Tools for AutoCAD Users (1st ed.). Boca Raton, FL: CRC Press. ISBN 978-1-4822-5290-3.
  5. ^ R. J. Light; D. B. Pillemer (1984). Summing up: The Science of Reviewing Research. Cambridge, Massachusetts.: Harvard University Press.
  6. ^ M. Egger, G. Davey Smith, M. Schneider & C. Minder (September 1997). "Bias in meta-analysis detected by a simple, graphical test". BMJ. 315 (7109): 629–634. doi:10.1136/bmj.315.7109.629. PMC 2127453. PMID 9310563.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  7. ^ Galbraith, Rex (1988). "Graphical display of estimates having differing standard errors". Technometrics. American Society for Quality. 30 (3): 271–281. doi:10.2307/1270081. JSTOR 1270081.
  8. ^ 제시카 M.See Through Statistics 제3판, Thomson Brooks/Cole, 2005, 페이지 166–167.ISBN 0-534-39402-7
  9. ^ Theodore T. Allen (2010). Introduction to Engineering Statistics and Lean Sigma: Statistical Quality Control and Design of Experiments and Systems. Springer. p. 128. ISBN 978-1-84882-999-2. Retrieved 2011-02-17.
  10. ^ Hintze Jerry L.; Nelson Ray D. (1998). "Violin Plots: A Box Plot-Density Trace Synergism". The American Statistician. 52 (2): 181–84. doi:10.1080/00031305.1998.10480559.

외부 링크

Wikimedia Commons에는 플롯과 관련된 미디어가 있습니다.
  • itl.nist.gov에 있는 유용한 그래픽 기술의 데이터 슬롯 갤러리.